NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory

Download PDF

NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory - Exercise Questions

Q13.1 Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3 Å.

Answer:

The diameter of an oxygen molecule, d = 3 Å.

The actual volume of a mole of oxygen molecules V _actual is

$\\V_{actual}=N_{A}\frac{4}{3}\pi \left ( \frac{d}{2} \right )^{3}\\ V_{actual}=6.023\times 10^{23}\times \frac{4}{3}\pi \times \left ( \frac{3\times 10^{-10}}{2} \right )^{3}\\ V_{actual}=8.51\times 10^{-6}m^{3}\\ V_{actual}=8.51\times 10^{-3}litres$

The volume occupied by a mole of oxygen gas at STP is V _molar = 22.4 litres

$\\\frac{V_{actual}}{V_{molar}}=\frac{8.51\times 10^{-3}}{22.4}\\ \frac{V_{actual}}{V_{molar}}=3.8\times 10^{-4}$

Q13.2 Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, $0^{0}C$ ). Show that it is $22.4 Litres$ .

Answer:

As per the ideal gas equation

$\\PV=nRT\\ V=\frac{nRT}{P}$

For one mole of a gas at STP we have

$\\V=\frac{1\times 8.314\times 273}{1.013\times 10^{5}}\\ V=0.0224 m^{3}\\ V=22.4\ litres$

Q13.3 Figure 13.8 shows plot of $PV/T$ versus P for $1.00\times 10^{-3}$ kg of oxygen gas at two different temperatures.

1650449178452

(a) What does the dotted plot signify?
(b) Which is true: $T_{1}> T_{2}\: \: orT_{1}< T_{2}$ ?
(c) What is the value of $PV/T$ where the curves meet on the y-axis?
(d) If we obtained similar plots for $1.00\times 10^{-3}$ kg of hydrogen, would we get the same
value of $PV/T$ at the point where the curves meet on the y-axis? If not, what mass
of hydrogen yields the same value of $PV/T$ (for low pressure high temperature
region of the plot) ? (Molecular mass of $H_{2}=2.02\mu$ , of $O_{2}=32.0\mu$ ,
$R=8.31J mol^{-1}K^{-1}$ .)

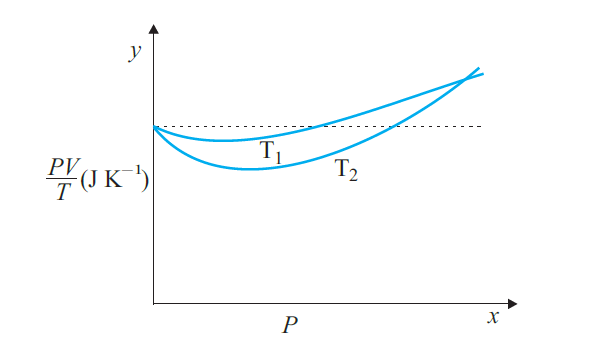
Answer:

(a) The dotted plot corresponds to the ideal gas behaviour.

(b) We know the behaviour of a real gas tends close to that of ideal gas as its temperature increases and since the plot corresponding to temperature T ₁ is closer to the horizontal line that the one corresponding to T ₂ we conclude T ₁ is greater than T ₂ .

$\frac{PV}{T}=nR$

The molar mass of oxygen = 32 g

$n=\frac{1}{32}$

R = 8.314

$\\nR=\frac{1}{32}\times 8.314\\ nR=0.256JK^{-1}$

(d) If we obtained similar plots for $1.00\times 10^{-3}$ kg of hydrogen we would not get the same
value of $PV/T$ at the point where the curves meet on the y-axis as 1 g of Hydrogen would contain more moles than 1 g of Oxygen because of having smaller molar mass.

Molar Mass of Hydrogen M = 2 g

mass of hydrogen

$m=\frac{PV}{T} \frac{M}{R}={0.256}\times \frac{2}{8.314}=5.48\times10^{-5}Kg$

Q13.4 An oxygen cylinder of volume $30$ litres has an initial gauge pressure of $15$ atm and a temperature of $27^{0}C$ . After some oxygen is withdrawn from the cylinder, the gauge pressure drops to $11$ atm and its temperature drops to $17^{0}C$ . Estimate the mass of
oxygen taken out of the cylinder ( $R=8.31Jmol^{-1}K^{-1}$ , molecular mass of $O_{2}=32\mu$ ).

Answer:

Initial volume, V ₁ = Volume of Cylinder = 30 l

Initial Pressure P ₁ = 15 atm

Initial Temperature T ₁ = 27 ^o C = 300 K

The initial number of moles n ₁ inside the cylinder is

$\\n_{1}=\frac{P_{1}V_{1}}{RT_{1}}\\ n_{1}=\frac{15\times 1.013\times 10^{5}\times 30\times 10^{-3}}{8.314\times 300}\\ n_{1}=18.28$

Final volume, V ₂ = Volume of Cylinder = 30 l

Final Pressure P ₂ = 11 atm

Final Temperature T ₂ = 17 ^o C = 290 K

Final number of moles n ₂ inside the cylinder is

$\\n_{2}=\frac{P_{2}V_{2}}{RT_{2}}\\ n_{2}=\frac{11\times 1.013\times 10^{5}\times 30\times 10^{-3}}{8.314\times 290}\\ n_{2}=13.86$

Moles of oxygen taken out of the cylinder = n ₂ -n ₁ = 18.28 - 13.86 = 4.42

Mass of oxygen taken out of the cylinder m is

$\\m=4.42\times 32\\ m=141.44g$

Q13.5 An air bubble of volume $1.0 cm^{3}$ rises from the bottom of a lake $40m$ deep at a temperature of $12^{0}C$ . To what volume does it grow when it reaches the surface, which is at a temperature of $35^{0}C$ ?

Answer:

Initial Volume of the bubble, V ₁ = 1.0 cm ³

Initial temperature, T ₁ = 12 ^o C = 273 + 12 = 285 K

The density of water is $\rho _{w}=10^{3}\ kg\ m^{-3}$

Initial Pressure is P ₁

Depth of the bottom of the lake = 40 m

$\\P_{1}=Atmospheric\ Pressure+Pressure\ due\ to\ water\\ P_{1}=P_{atm}+\rho _{w}gh\\ P_{1}=1.013\times 10^{5}+10^{3}\times 9.8\times 40\\ P_{1}=4.93\times 10^{5}Pa$

Final Temperature, T ₂ = 35 ^o C = 35 + 273 = 308 K

Final Pressure = Atmospheric Pressure $=1.013\times 10^{5}Pa$

Let the final volume be V ₂

As the number of moles inside the bubble remains constant we have

$\\\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\\ V_{2}=\frac{P_{1}T_{2}V_{1}}{P_{2}T_{1}}\\ V_{2}=\frac{4.93\times 10^{5}\times 308\times 1}{1.013\times 10^{5}\times 285}\\ V_{2}=5.26\ cm^{3}$

Q13.6 Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity $25.0m^{3}$ at a temperature of $27^{0}C$ and $1atm$ pressure.

Answer:

The volume of the room, V = 25.0 m ³

Temperature of the room, T = 27 ^o C = 300 K

The pressure inside the room, P = 1 atm

Let the number of moles of air molecules inside the room be n

$\\n=\frac{PV}{RT}\\ n=\frac{1.013\times 10^{5}\times 25}{8.314\times 300}\\ n=1015.35$

Avogadro's Number, $N_{A}=6.022\times 10^{23}$

Number of molecules inside the room is N

$\\N=nN_{A}\\ N=1015.35\times 6.022\times 10^{23}\\ N=6.114\times 10^{26}$

Q13.7 Estimate the average thermal energy of a helium atom at (i) room temperature ( $27^{0}C$ ), (ii) the temperature on the surface of the Sun ( $6000K$ ), (iii) the temperature of $10$ million kelvin (the typical core temperature in the case of a star).

Answer:

The average energy of a Helium atom is given as $\frac{3kT}{2}$ since it is monoatomic

(i)

$\\E=\frac{3kT}{2}\\ E=\frac{3\times 1.38\times 10^{-23}\times 300}{2}\\ E=6.21\times 10^{-21}\ J$

(ii)

$\\E=\frac{3kT}{2}\\ E=\frac{3\times 1.38\times 10^{-23}\times 6000}{2}\\ E=1.242\times 10^{-19}\ J$

(iii)

$\\E=\frac{3kT}{2}\\ E=\frac{3\times 1.38\times 10^{-23}\times10^{7}}{2}\\ E=2.07\times 10^{-16}\ J$

Q13.8 Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is v _rms the largest?

Answer:

As per Avogadro's Hypothesis under similar conditions of temperature and pressure equal volumes of gases contain equal number of molecules. Since the volume of the vessels are the same and all vessels are kept at the same conditions of pressure and temperature they would contain equal number of molecules.

Root mean square velocity is given as

$v_{rms}=\sqrt{\frac{3kT}{m}}$

As we can see v _rms is inversely proportional to the square root of the molar mass the root mean square velocity will be maximum in case of Neon as its molar mass is the least.

Q13.9 At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at $-20^{0}C$ ? (atomic mass of $Ar=39.9\mu$ , of $He=4.0\mu$ ).

Answer:

As we know root mean square velocity is given as $v_{rms}=\sqrt{\frac{3RT}{M}}$

Let at temperature T the root mean square speed of an atom in an argon cylinder equal to the rms speed of a helium gas atom at $-20^{0}C$

$\\\sqrt{\frac{3R\times T}{39.9}}=\sqrt{\frac{3R\times 253}{4}}\\ T=2523.7\ K$

Q13.10 Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2.0 atm$ and temperature $17^{0}C$ . Take the radius of a nitrogen molecule to be roughly $1.0A$ . Compare the collision time with the time the
molecule moves freely between two successive collisions (Molecular mass of $N_{2}=28.0\mu$ ).

Answer:

Pressure, P = 2atm

Temperature, T = 17 ^o C

The radius of the Nitrogen molecule , $r=1\ \AA$

The molecular mass of N ₂ = 28 u

The molar mass of N ₂ = 28 g

From ideal gas equation

$\\PV=nRT\\ \frac{n}{V}=\frac{P}{RT}\\$

The above tells us about the number of moles per unit volume, the number of molecules per unit volume would be given as

$\\n'=\frac{N_{A}n}{V}=\frac{6.022\times 10^{23}\times 2\times 1.013\times 10^{5}}{8.314\times (17+273)}\\ n'=5.06\times 10^{25}$

The mean free path $\lambda$ is given as

$\\\lambda =\frac{1}{\sqrt{2}\pi n'd^{2}}\\ \lambda =\frac{1}{\sqrt{2}\times \pi \times 5.06\times 10^{25}\times (2\times 1\times 10^{-10})^{2}}\\ \lambda =1.11\times 10^{-7}\ m$

The root mean square velocity v _rms is given as

$\\v_{rms}=\sqrt{\frac{3RT}{M}}\\ v_{rms}=\sqrt{\frac{3\times 8.314\times 290}{28\times 10^{-3}}}\\ v_{rms}=508.26\ m\ s^{-1}$

The time between collisions T is given as

$\\T=\frac{1}{Collision\ Frequency}\\ T=\frac{1}{\nu }\\ T=\frac{\lambda }{v_{rms}}\\ T=\frac{1.11\times 10^{-7}}{508.26}\\ T=2.18\times 10^{-10}s$

Collision time T' is equal average time taken by a molecule to travel a distance equal to its diameter

$\\T'=\frac{d}{v_{rms}}\\ T'=\frac{2\times 1\times 10^{-10}}{508.26}\\ T'=3.935\times 10^{-13}s$

The ratio of the average time between collisions to the collision time is

$\\\frac{T}{T'}=\frac{2.18\times 10^{-10}}{3.935\times 10^{-13}}\\ \frac{T}{T'}=554$

Thus we can see time between collisions is much larger than the collision time.

NCERT solutions for class 11 physics chapter 13 kinetic theory - Additional Exercise Questions

Q13.11 A metre long narrow bore held horizontally (and closed at one end) contains a $76 cm$ long mercury thread, which traps a $15 cm$ column of air. What happens if the tube is held vertically with the open end at the bottom?

Answer:

Initially, the pressure of the 15 cm long air column is equal to the atmospheric pressure, P ₁ = 1 atm = 76 cm of Mercury

Let the crossectional area of the tube be x cm ²

The initial volume of the air column, V ₁ = 15x cm ³

Let's assume once the tube is held vertical y cm of Mercury flows out of it.

The pressure of the air column after y cm of Mercury has flown out of the column P ₂ = 76 - (76 - y) cm of Mercury = y cm of mercury

Final volume of air column V ₂ = (24 + y)x cm ³

Since the temperature of the air column does not change

$\\P_{1}V_{1}=P_{2}V_{2}\\ 76\times 15x=y\times (24+y)x\\ 1140=y^{2}+24y\\ y^{2}+24y-1140=0$

Solving the above quadratic equation we get y = 23.8 cm or y = -47.8 cm

Since a negative amount of mercury cannot flow out of the column, y cannot be negative. Therefore y = 23.8 cm.

Length of the air column = y + 24 = 47.8 cm.

Therefore once the tube is held vertically, 23.8 cm of Mercury flows out of it and the length of the air column becomes 47.8 cm

Q 13.12 From a certain apparatus, the diffusion rate of hydrogen has an average value of $28.7cm^{3}s^{-1}$ . The diffusion of another gas under the same conditions is measured to have an average rate of $7.2cm^{3}s^{-1}$ . Identify the gas.

Answer:

As per Graham's Law of diffusion if two gases of Molar Mass M ₁ and M ₂ diffuse with rates R ₁ and R ₂ respectively their diffusion rates are related by the following equation

$\frac{R_{1}}{R_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}$

In the given question

R ₁ = 28.7 cm ³ s ^-1

R ₂ = 7.2 cm ³ s ^-1

M ₁ = 2 g

$\\M_{2}=M_{1}\left ( \frac{R_{1}}{R_{2}} \right )^{2}\\ M_{2}=2\times \left ( \frac{28.7}{7.2} \right )^{2}\\ M_{2}=31.78g$

The above Molar Mass is close to 32, therefore, the gas is Oxygen.

Q13.13 A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres $n_{2}=n_{1}exp\left [ -mg(h_{2}-h_{1}) /k_{b}T\right ]$

where n2, n1 refer to number density at heights h2 and h1 respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column:

$n_{2}=n_{1}exp\left [ -mg N_{A}(\rho -\rho ^{'})(h_{2}-h_{1})/ (\rho RT)\right ]$
where $\rho$ is the density of the suspended particle, and $\rho ^{'}$ , that of the surrounding medium. [ $N_{A}$ s Avogadro’s number, and R the universal gas constant.] [Hint: Use Archimedes principle to find the apparent weight of the suspended particle.]

Answer:

$n_{2}=n_{1}exp\left [ -mg(h_{2}-h_{1}) /k_{b}T\right ]$ $(i)$

Let the suspended particles be spherical and have radius r

The gravitational force acting on the suspended particles would be

$F_{G}=\frac{4}{3}\pi r^{3}\rho g$

The buoyant force acting on them would be

$F_{B}=\frac{4}{3}\pi r^{3}\rho' g$

The net force acting on the particles become

$\\F_{net}=F_{G}-F_{B}\\ F_{net}=\frac{4}{3}\pi r^{3}\rho g-\frac{4}{3}\pi r^{3}\rho' g\\F_{net}=\frac{4}{3}\pi r^{3}g(\rho -\rho ')$

Replacing mg in equation (i) with the above equation we get

$\\n_{2}=n_{1}exp\left [ -\frac{4}{3}\pi r^{3}g(\rho -\rho ')(h_{2}-h_{1}) /k_{b}T\right ]\\ n_{2}=n_{1}exp\left [ \frac{-\frac{4}{3}\pi r^{3}g(\rho -\rho ')(h_{2}-h_{1})}{\frac{RT}{N_{A}}} \right ]\\ n_{2}=n_{1}exp\left [ \frac{-mgN_{A}(\rho -\rho ')(h_{2}-h_{1})}{RT\rho '} \right ]$

The above is the equation to be derived

Q13.14 Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms :

Substance	Atomic Mass (u)	Density (10 ³ Kg m ³ )
Carbon (diamond)	12.01	2.22
Gold	197	19.32
Nitrogen (liquid)	14.01	1
Lithium	6.94	0.53
Fluorine	19	1.14

Answer:

Let one mole of a substance of atomic radius r and density $\rho$ have molar mass M

Let us assume the atoms to be spherical

Avogadro's number is $N_{A}=6.022\times 10^{23}$

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3M}{4N_{A}\pi \rho } \right )^{\frac{1}{3}}$

For Carbon

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3\times 12.01}{4\times 6.022\times 10^{23}\times \pi\times 2.22\times 10^{3} } \right )^{\frac{1}{3}}\\ r=1.29\AA$

For gold

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3\times 197.00}{4\times 6.022\times 10^{23}\times \pi\times 19.32\times 10^{3} } \right )^{\frac{1}{3}}\\ r=1.59\AA$

For Nitrogen

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3\times 14.01}{4\times 6.022\times 10^{23}\times \pi\times 1.00\times 10^{3} } \right )^{\frac{1}{3}}\\ r=1.77\AA$

For Lithium

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3\times 6.94}{4\times 6.022\times 10^{23}\times \pi\times 0.53\times 10^{3} } \right )^{\frac{1}{3}}\\ r=1.73\AA$

For Fluorine

$\\N_{A}\frac{4}{3}\pi r^{3}\rho =M\\ r=\left ( \frac{3\times19.00}{4\times 6.022\times 10^{23}\times \pi\times 1.14\times 10^{3} } \right )^{\frac{1}{3}}\\ r=1.88\AA$

Class 11 physics ch 13 ncert solutions are essential for comprehending how tiny particles in matter behave. This chapter helps students understand how gases work and their thermal properties. It also connects to other chapters in thermodynamics and has practical applications. By studying this chapter, students can do well in their exams and gain a solid understanding of how matter works on a fundamental level.

NCERT Solutions for Class 11 Physics Chapter Wise

Chapter 1	Physical world
Chapter 2	Units and Measurement
Chapter 3	Motion in a Straight Line
Chapter 4	Motion in a Plane
Chapter 5	Laws of Motion
Chapter 6	Work, Energy and Power
Chapter 7	System of Particles and Rotational motion
Chapter 8	Gravitation
Chapter 9	Mechanical Properties of Solids
Chapter 10	Mechanical Properties of Fluids
Chapter 11	Thermal Properties of Matter
Chapter 12	Thermodynamics
Chapter 13	Kinetic Theory
Chapter 14	Oscillations
Chapter 15	Waves

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

kinetic theory of gases class 11 physics NCERT solutions: Important Formulas and Diagrams

The ideal gas equation is given by

$PV=\mu RT=K_BNT$

where $\mu$ is the number of moles

N is the number of molecules

R and k _B are universal constants.

The pressure of an ideal gas

$P=\frac{1}{3}nm\bar v^2$

where n is the number density, m is the mass of the molecule and $\bar v^2$ is the mean of the squared speed.

The RMS velocity of the gas molecule

$v_{rms}=\sqrt{\bar v^2}=\sqrt{\frac{3K_BT}{m}}$ Where T is the temperature.

The translational kinetic energy is

$\frac{3K_BNT}{2}$

The mean free path

$l=\frac{1}{\sqrt{2}n\pi d^2}$

where n is the number density and d is the diameter of the molecule

Use of NCERT Solutions For Class 11 Physics Chapter 13 Kinetic Theory

To familiarise yourself with the concepts studied in the chapter, it is important to study the CBSE NCERT solutions for Class 11 Physics Chapter 13 Kinetic Theory.
All the equations studied in the chapter are utilized in the solutions of NCERT Class 11 Physics Chapter 13 Kinetic Theory.
The NCERT solutions for Class 11 are important for class exams and competitive exams. For exams like NEET and JEE Mains, one question can be expected from the chapter and the questions can be solved easily if you are familiar with the concepts and formulas of the chapter.

Key Features of Class 11 physics ch 13 NCERT solutions 13 Kinetic Theory

Comprehensive Coverage: These kinetic theory of gases exercise solutions cover all the important topics and concepts presented in the chapter, ensuring a thorough understanding of kinetic theory.
Exercise and Additional Exercise Solutions: Detailed kinetic theory of gases class 11 physics ncert solutions for exercise questions (13.1 to 13.10) and additional exercise questions (13.11 to 13.14) are provided, facilitating practice and self-assessment.
Clarity and Simplicity: The kinetic theory of gases class 11 questions and answers are explained in clear and simple language, making complex concepts more accessible to students.
Problem-Solving Skills: By practising with these kinetic theory class 11 solutions, students develop strong problem-solving skills, which are essential in physics and other subjects.
Exam Preparation: These kinetic theory of gases exercise solutions are designed to help students prepare effectively for their exams, including board exams and competitive exams like JEE and NEET.

Dropped Topics –

13.6.5 - Specific Heat Capacity of Water
Exercises - (13.11–13.14)

NCERT solutions for class 11 Subject wise

NCERT Solutions for Class 11 Biology

NCERT Solutions for Class 11 Maths

NCERT Solutions for Class 11 Chemistry

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

We trust that the kinetic theory of gases class 11 questions and answers prove to be beneficial for your studies. If you have any questions or require further clarification regarding these solutions, please feel free to leave a comment below, and we will promptly address your inquiries.

Frequently Asked Questions (FAQs)

1. What is the weightage of the Class 11 Physics chapter Kinetic Theory for JEE Main and NEET

For both JEE Main and NEET one question can be expected from the chapter Kinetic Theory. To practice more problems on Kinetic Theory refer to NCERT book questions, NCERT exemplar questions and previous year papers of NEET and JEE Main.

2. What are the topics covered in Kinetic Theory Class 11 Physics NCERT book?

The following are the topics covered in Class 11 chapter Kinetic Theory

Molecular nature of matter
Behaviour of gases
Kinetic theory of an ideal gas
Law of equipartition of energy
Specific heat capacity
Mean free path

3. What is Kinetic Theory

The gas consists of rapidly moving atoms or molecules. Kinetic theory explains the behaviour of gas based on these rapidly moving molecules.

4. A fluid is filled inside a container. Is there exist a pressure at the center of the container?

Pressure exists everywhere in a fluid, not only the walls of the container. Any layer of gas inside the volume of a container is in equilibrium because the pressure is the same on both sides of the layer.

Also Read

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Class 11 Biology Chapter 19 Notes Excretory Products And Their Elimination- Download PDF Notes

NCERT Class 11 Biology Chapter 22 Notes Chemical Coordination And Integration- Download PDF Notes

Some basic concepts of Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 1 Notes - Download PDF

NCERT Class 11 Biology Chapter 21 Notes Neural Control And Coordination- Download PDF Notes

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

Silverzone ABHO Result 2024-25 - Check Akhil Bhartiya Hindi Olympiad Results Here

Nov 20, 2024

Silverzone SKGKO Result 2024-25 – Check Your Scores and Performance

Nov 20, 2024

Education Loan for School Students in India – Eligibility, Benefits & Application Process

Nov 20, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Nov 20, 2024

Silverzone SKGKO Answer Key 2024-25: Download Smart Kid GK Olympiad Answer Key @ silverzone.org

Nov 20, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Nov 20, 2024

ICICI Education Loan: Eligibility, Interest Rates & Application Process

Nov 19, 2024

MPSOS 10th Result 2024 - Check MPSOS Class 10 December 2024 Exam Result @mpsos.nic.in

Nov 16, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Mock Test

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Result

Mock Test

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Admit Card

Result

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

Exam Pattern

Result

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory

NCERT Solutions Class 11 Physics Chapter 13 – Free PDF Access

NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory

NCERT solutions for class 11 physics chapter 13 kinetic theory - Additional Exercise Questions

NCERT Solutions for Class 11 Physics Chapter Wise

kinetic theory of gases class 11 physics NCERT solutions: Important Formulas and Diagrams

Use of NCERT Solutions For Class 11 Physics Chapter 13 Kinetic Theory

Key Features of Class 11 physics ch 13 NCERT solutions 13 Kinetic Theory

NCERT solutions for class 11 Subject wise

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

National Institute of Open Schooling 10th examination

Mizoram Board of School Education 12th Examination

Mizoram Board 10th Examination

Punjab Board of Secondary Education 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app