NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.2 - Circles
Suppose a horizontal line PQ and a point O in a plane. From O to PQ line, many lines join O to PQ, and you will get many lines like OL1, OL2, OL3 and so on. These lines are called a line segment. But in these line segments, which one will be the distance between O and PQ? As shown in the figure, OM is the distance between O and line PQ. OM is called the least distance between O and the line PQ. In other words, the line that is perpendicular to a line is called the distance of the line from the point, and this perpendicular line makes an angle of 90oas shown in the figure: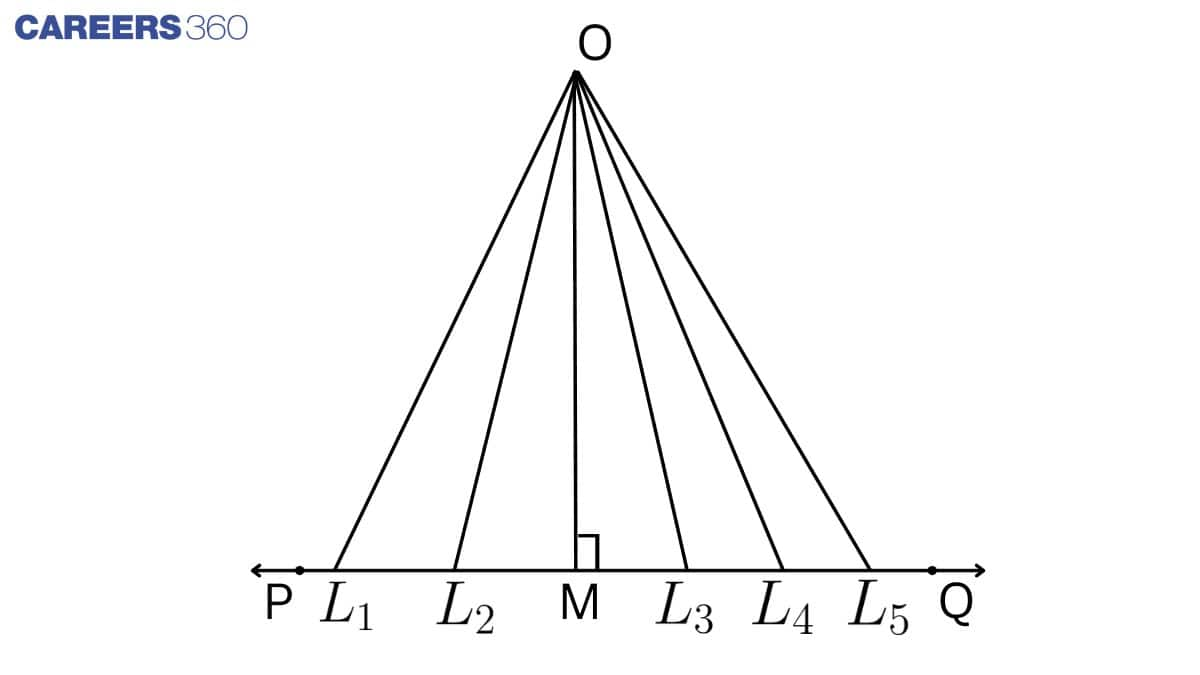
This Story also Contains
- NCERT Solutions for Class 9 Maths Chapter 9 – Circles Exercise 9.2
- Access Circles Class 9 Maths Chapter 9 – Exercise 9.2
- Topics Covered in Chapter 9 Circles: Exercise 9.2
- NCERT Solutions of Class 9 Subject Wise
- NCERT Subject-Wise Exemplar Solutions

The 9th class maths exercise 9.2 consists of six questions expertly developed by our Subject Matter Expert. These class 9 maths chapter 9 exercise 9.2 provide students with complete help by providing extensive, step-by-step explanations. PDF versions are also freely accessible for download to increase the accessibility and convenience of the students. NCERT Solutions are designed by our subject matter expert to provide students with easy access to content according to the NCERT books.
**Please be aware that this chapter has been renumbered as Chapter 9 in the CBSE Syllabus for the academic year 2024-25.
Access Circles Class 9 Maths Chapter 9 – Exercise 9.2
Q1 Two circles of radii 5cm and 3cm intersect at two points and the distance between their centres is 4cm . Find the length of the common chord.
Solution:
Given: Two circles of radii 5cm and 3cm intersect at two points and the distance between their centres is 4cm .
To find the length of the common chord.
Construction: Join OP and ON draw $OM\perp AB\
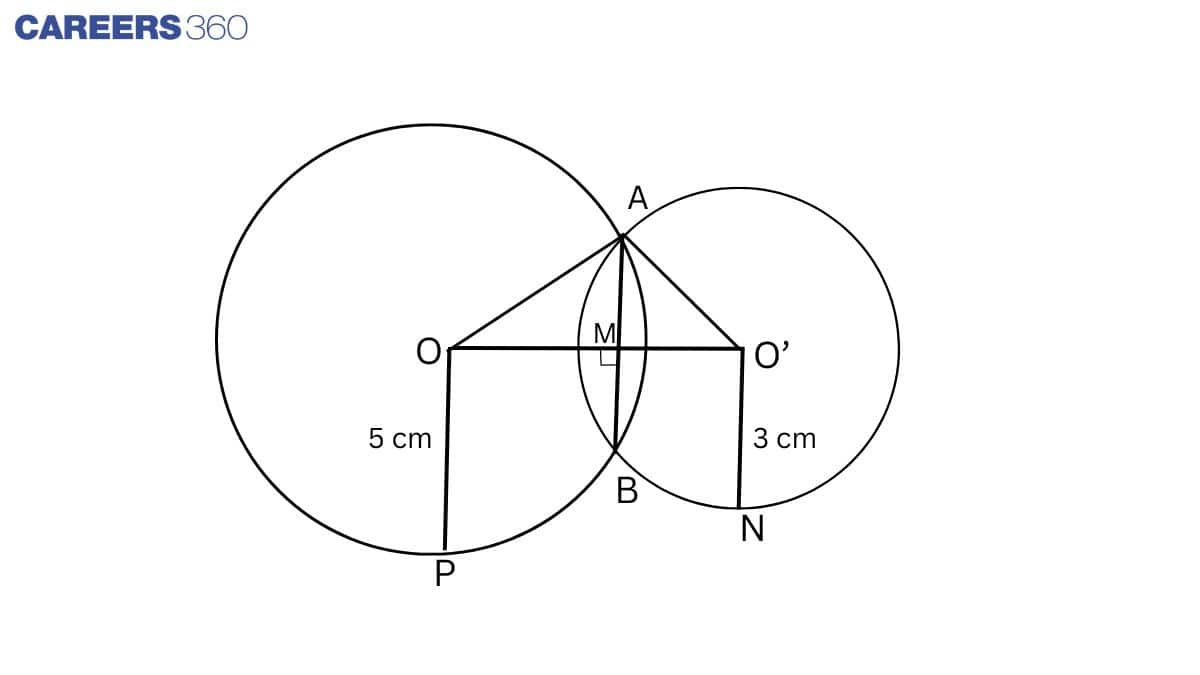
Proof: AB is a chord of the circle, and OM is the bisector of chord AB.
∴OM⊥AB
∠OMA=90∘
Let, OM = x , so O'M = 4 - x
In △ AOM, using Pythagoras' theorem
AM2=AO2−OM2 ...........................(1)
Also,
In △ AO'M, using Pythagoras' theorem
AM2=AO′2−MO′2 ...........................(2)
From (1) and (2), we get
AO2−OM2=AO′2−MO′2
⇒52−x2=32−(4−x)2
⇒25−x2=9−16−x2+8x
⇒32=8x
⇒x=4
Put x = 4 in equation (1)
AM2=52−42=9
⇒AM=3
⇒AB=2AM=6
Q2 If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Given: two equal chords of a circle intersect within the circle.
To prove: Segments of one chord are equal to corresponding segments of the other chord i.e. AP = CP and BP = DP.
Construction: Join OP and draw OM⊥ABandON⊥CD.
Proof: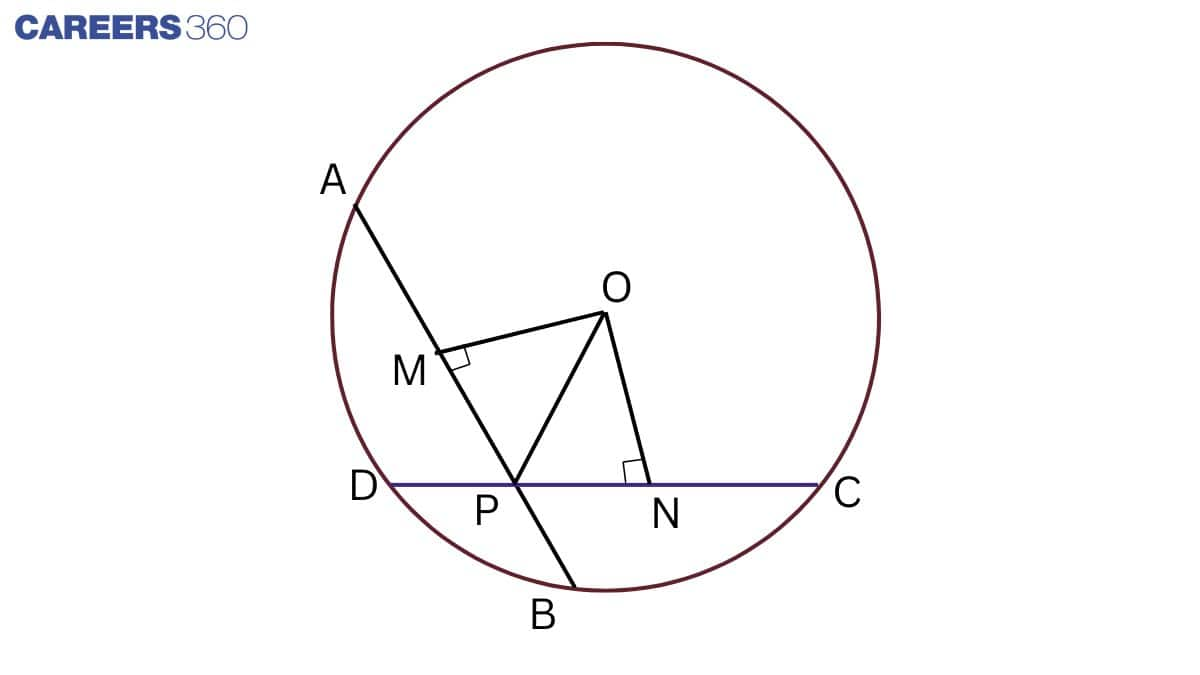
In △ OMP and △ ONP,
OP = OP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
∠ OMP = ∠ ONP (Both are right angled)
Thus, △ OMP ≅ △ ONP (By SAS rule)
PM = PN..........................(1) (CPCT)
AB = CD ..........................(2)(Given)
⇒12AB=12CD
⇒AM=CN .....................(3)
Adding equations (1) and (3), we have
AM + PM = CN + PN
⇒AP=CP .................(4)
Subtract equation (4) from (2), we get
AB−AP=CD−CP
⇒PB=PD
Q3 If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
Given: two equal chords of a circle intersect within the circle.
To prove: the line joining the point of intersection to the centre makes equal angles with the chords.
i.e. ∠ OPM= ∠ OPN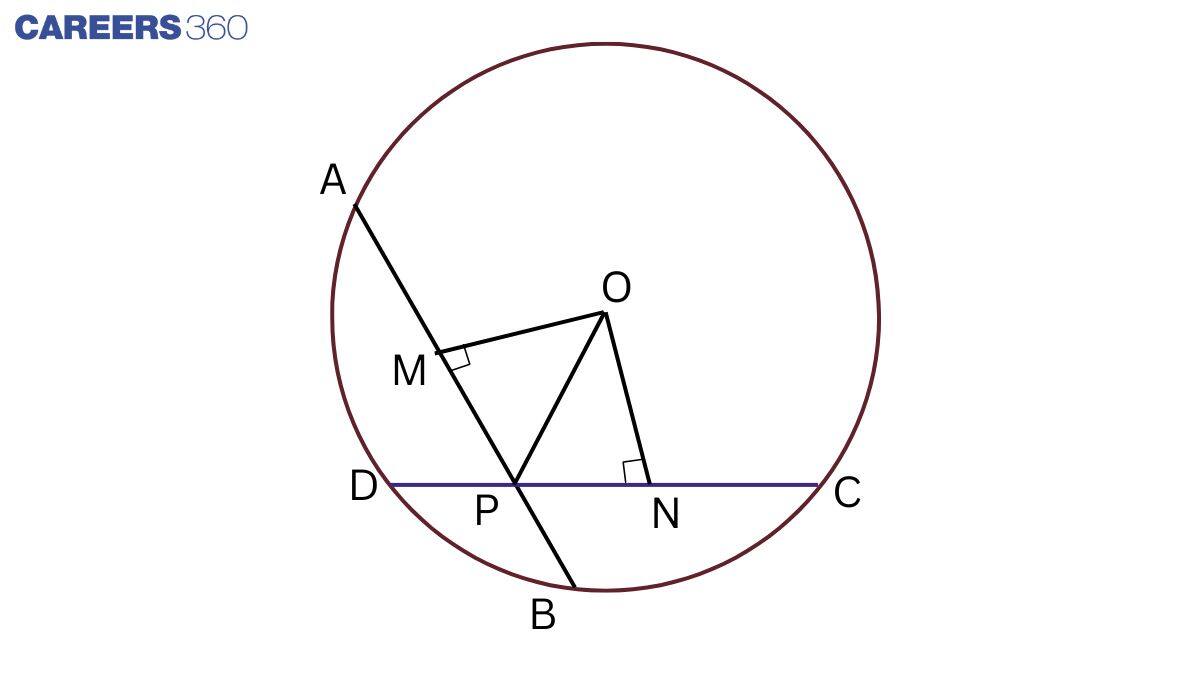
Proof:
Construction: Join OP and draw OM⊥ABandON⊥CD.
In △ OMP and △ ONP,
OP = OP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
∠ OMP = ∠ ONP (Both are right-angled)
Thus, △ OMP ≅ △ ONP (By RHS rule)
∠ OPM= ∠ OPN (CPCT)
Solution:
Given: a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D.
To prove: AB = CD
Construction: Draw OM⊥AD
Proof: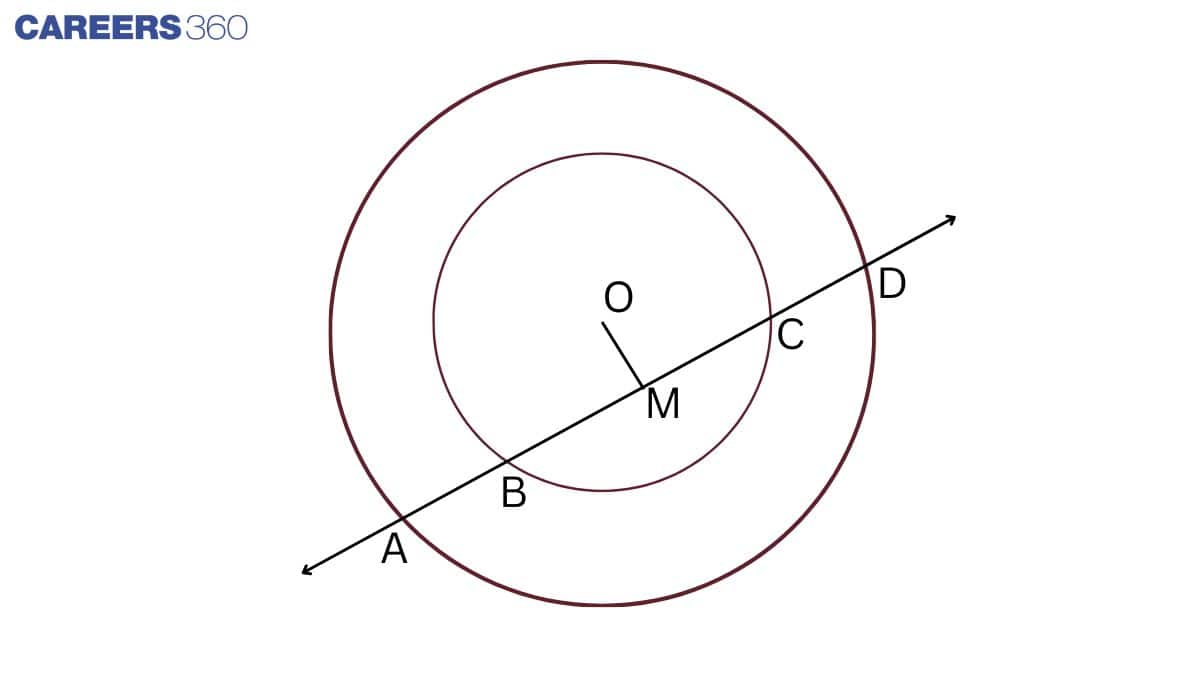
BC is a chord of the inner circle and OM⊥BC
So, BM = CM .................(1)
(Perpendicular OM bisect BC)
Similarly,
AD is a chord of the outer circle and OM⊥AD
So, AM = DM .................(2) (Perpendicular OM bisect AD)
Subtracting equation (1) from (2), we get
AM−BM=DM−CM
⇒AB=CD
Solution:
Given: From the figure, R, S, and M are the positions of Reshma, Salma, and Mandip, respectively.
So, RS = SM = 6 cm
Construction: Join ON, OS, OR and OM. Draw OL⊥RS.
Proof: 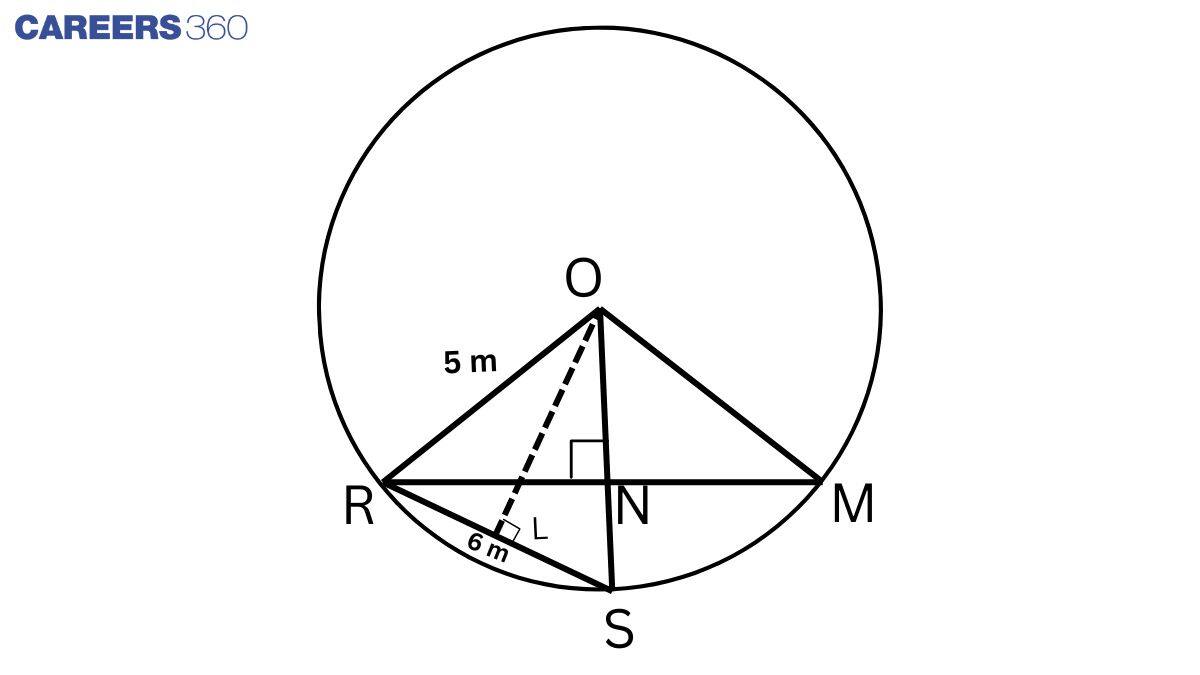
In △ ORS,
OS = OR and OL⊥RS (by construction)
So, RL = LS = 3cm (RS = 6 cm)
In △ OLS, by Pythagoras' theorem,
OL2=OS2−SL2
⇒OL2=52−32=25−9=16
⇒OL=4
In △ ORN and △ OMN,
OR = OM (Radii)
∠ RON = ∠ MON (Equal chords subtend equal angles at the centre)
ON = ON (Common)
△ ORN ≅ △ OMN (By SAS)
RN = MN (CPCT)
Thus, ON⊥RM
Area of △ ORS = 12×RS×OL ..................(1)
Area of △ ORS = 12×OS×NR ..................(2)
From 1 and 2, we get
12×RS×OL =12×OS×NR
⇒RS×OL=OS×KR
⇒6×4=5×KR
⇒NR=4.8cm
Thus, RM=2NR=2×4.8cm=9.6cm
Solution:
Given: In the figure, A, B, and C are positioned as Ankur, Syed and David, respectively.
So, AB = BC = CD
Radius of circular park = 20m
So, AO = OB = OC = 20m
Construction: AF ⊥ BC
Proof:
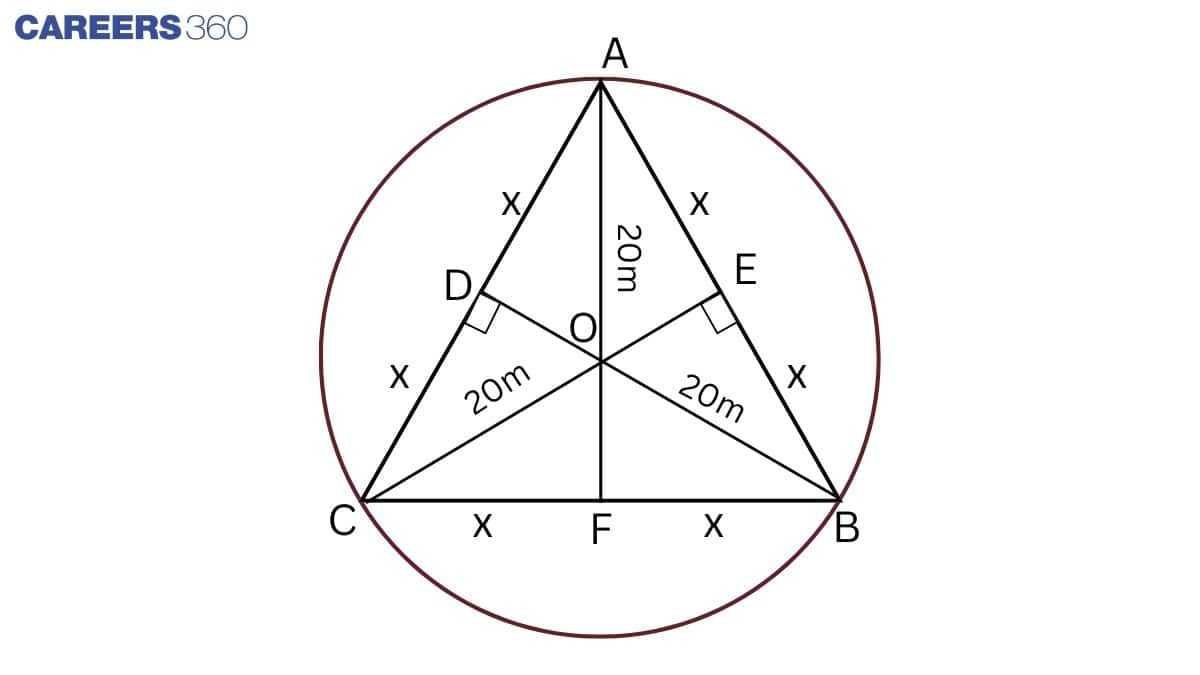
Let AC = CB = AB = 2x cm
In △ ABC,
AC = AB and AF ⊥ BC
So, CF = FB = x cm
In △ OFB, by Pythagoras,
OF2=OB2−FB2
⇒OF2=202−x2=400−x2
⇒OF=400−x2
In △ AFB, by Pythagoras,
AF2=AB2−FB2
⇒(AO+OF)2+x2=(2x)2
⇒(20+400−x2)2+x2=4x2
⇒400+400−x2+40400−x2+x2=4x2
⇒800+40400−x2=4x2
⇒200+10400−x2=x2
⇒10400−x2=x2−200
Squaring both sides,
⇒100(400−x2)=(x2−200)2
⇒40000−100x2=x4−40000−400x2
⇒x4−300x2=0
⇒x2(x2−300)=0
⇒x2=300
⇒x=103
Hence, the length of the string of each phone =2x=203 m
Also Read:
Topics Covered in Chapter 9 Circles: Exercise 9.2
This exercise includes some important theorems about two equal chords from an examination point of view. We'll start with a definition of a chord.
Chord: A chord is a straight line segment with both ends on the circle's perimeter. Its Latin translation is 'bowstring.'
The length of the perpendicular from a point to a line defines the distance between them.
Theorem:
A circle's equal chords (or congruent circles' equal chords) are equidistant from the centre (or centres).
Chords that are equidistant from the circle's centre have the same length.
- The diameter is the longest chord, and all diameters are the same length: twice the radius.
- An arc is a circle segment that connects two points. In a circle, equal chords have equal arcs.
- A chord that passes through the centre is referred to as a diameter.
- The circumference of a circle is the measurement of its circumference.
- A segment of the circle is the area between a chord and one of its arcs.
- A sector is an area between an arc and the two radii that connect the arc's centre and endpoints.
Also, See:
NCERT Solutions of Class 9 Subject Wise
Students must check the NCERT solutions for Class 9 Maths and Science given below:
NCERT Subject-Wise Exemplar Solutions
Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:
Frequently Asked Questions (FAQs)
In this exercise, we learn about the chords and their related theorems such as Chords that are equidistant from the circle's centre have the same length.
The largest chord subtends the right angle on the circumference.
NO, because equal chords can be infinite.
The subtended angle of the chord at a position on the major arc is 30. An equilateral triangle has 60 degrees on each side. An arc of a circle at its centre has double the angle of any other point of the circle.
Because its endpoints are on the circle's circumference, every diameter is a chord. It's the longest chord that runs through the circle's centre.
However, as every chord does not pass through the centre, every chord cannot be a diameter.
Concyclic points are a group of points that all lie in the same circle.
False, because a major arc's measure is more than 180° and equal to 360° minus the minor arc's measure with the same endpoints.
The length of OF is also 5cm because Chords that are equidistant from the circle's centre have the same length.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
