NCERT Solutions for Class 9 Maths Chapter 7 help students understand triangles through clear explanations of congruence and their properties. This step-by-step approach makes criteria like SSS, SAS, ASA, and RHS easy to apply in problems and proofs. Practising these solutions strengthens logical reasoning and accuracy. Overall, they prepare students well for exams and higher-level geometry concepts.
NCERT Solutions for Class 9 Maths Chapter 7 Triangles
A triangle is a geometrical shape having three sides and three angles. We can see different shapes around us that resemble a triangle, such as a slice of pizza, a clothes hanger, etc. Triangles are one of the important topics in the Class 9 NCERT syllabus. In this chapter, students learn about special types of triangles, such as equilateral triangles, isosceles triangles, and right-angled triangles, among others. It introduces the concept of congruency of triangles, wherein triangles are said to be congruent if they have identical form and length. The chapter explains important congruence rules such as SSS, SAS, AAS, and RHS. It also covers the properties of triangles, inequalities in triangles, and basic theorems such as the angle-sum property. The main benefit of NCERT Solutions for Class 9 Maths is that they explain answers clearly, making learning simpler and more effective.
This Story also Contains
- Triangles Class 9 Questions And Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 7 Triangles: Exercise Questions
- Triangles Class 9 NCERT Solutions: Exercise-wise
- Class 9 Maths NCERT Chapter 7 Solutions: Extra Questions
- Triangles Class 9 Chapter 7: Topics
- NCERT Triangles Class 9 Solutions: Important Formulae And Points
- Properties of Congruent Triangles
- Approach to Solve Questions of Triangles Class 9
- Why are Class 9 Maths Chapter 7 Triangles Question Answers Important?
- NCERT Solutions for Class 9 Chapter Wise
- NCERT Books and NCERT Syllabus
Triangles are the building blocks of geometry. These NCERT Solutions for Class 9 are trustworthy and reliable because they are created by subject-matter experts at Careers360, making them an essential resource for exam preparation. By using the solutions, you can prepare well for your school-level exams and create a strong foundation for competitive examinations. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus. For complete syllabus coverage, solved exercises, and exemplar solutions, check out this NCERT article.
Also, read,
Triangles Class 9 Questions And Answers PDF Free Download
To make maths learning easier, Careers360 experts have created these NCERT Solutions for Class 9 Maths Chapter 7 Triangles. A downloadable PDF has been provided—click the link below to access it.
NCERT Solutions for Class 9 Maths Chapter 7 Triangles: Exercise Questions
Below you will find NCERT Class 9 Maths Chapter 7 Triangles question answers explained step by step.
| Triangles Class 9 Question Answers Exercise: 7.1 Total Questions: 8 Page number: 92-94 |
Answer:
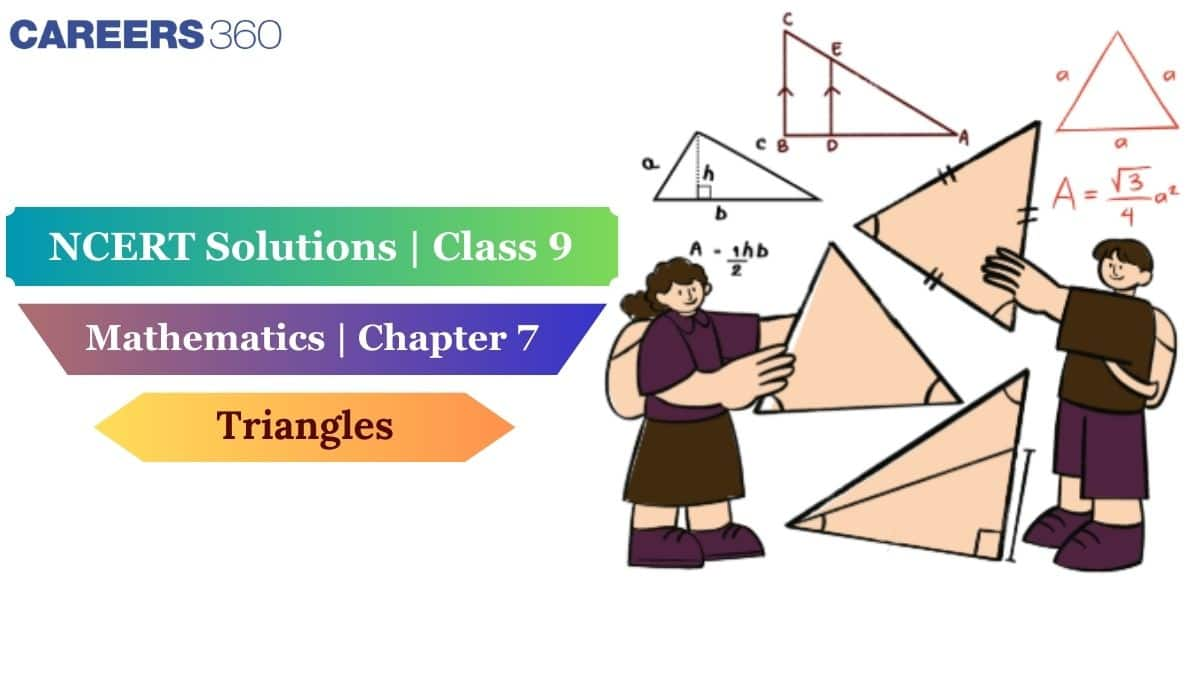
In the given triangles, we are given that:-
(i) $\small AC=AD$
(ii) Further, it is given that AB bisects angle A. Thus $\angle$ BAC $=\ \angle$ BAD.
(iii) Side AB is common to both triangles. $AB=AB$
Hence, by SAS congruence, we can say that: $\small \Delta ABC\cong \Delta ABD$
By c.p.c.t. (corresponding parts of congruent triangles are equal), we can say that $BC\ =\ BD$
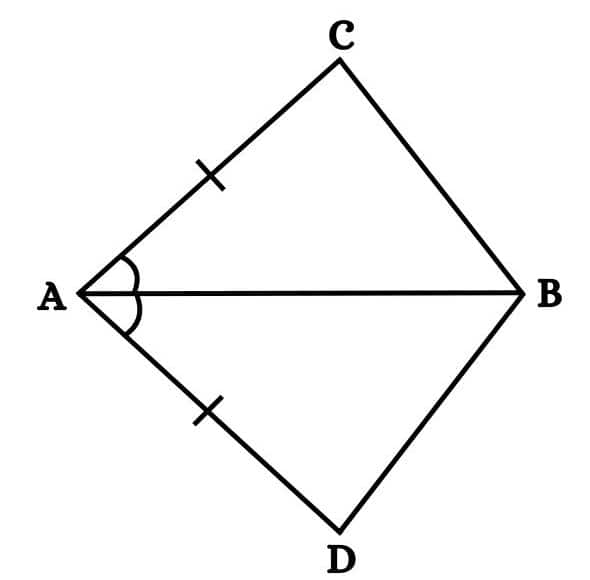
Question 2: (i) $ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB= \angle CBA$ (see Fig. ). Prove that $\small \Delta ABD\cong \Delta BAC$ .
Answer:
It is given that:-
(i) AD = BC
(ii) $\small \angle DAB= \angle CBA$
(iii) Side AB is common to both the triangles.
So, by SAS congruence, we can write :
$\small \Delta ABD\cong \Delta BAC$
Question 2: (ii) $\small ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB=\angle CBA$ (see Fig.). Prove that $\small BD=AC$
Answer:
In the previous part, we have proved that $\small \Delta ABD\cong \Delta BAC$.
Thus by c.p.c.t. , we can write : $\small BD=AC$
Question 2: (iii) $\small ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB= \angle BAC$ (see Fig.). Prove that $\small \angle ABD= \angle BAC$ .
Answer:
In the first part, we have proved that $\small \Delta ABD\cong \Delta BAC$.
Thus by c.p.c.t. , we can conclude :
$\small \angle ABD= \angle BAC$
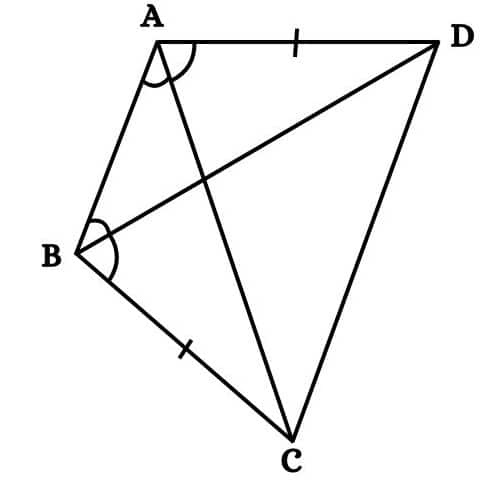
Answer:
In the given figure, consider $\Delta$ AOD and $\Delta$ BOC.
(i) AD = BC (given)
(ii) $\angle$ A = $\angle$ B (given that the line AB is perpendicular to AD and BC)
(iii) $\angle$ AOD = $\angle$ BOC (vertically opposite angles).
Thus, by the AAS Postulate, we have
$\Delta AOD\ \cong \ \Delta BOC$
Hence by c.p.c.t. we can write : $AO\ =\ OB$
And thus CD bisects AB.
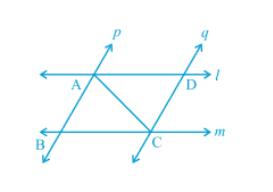
Answer:
In the given figure, consider $\Delta$ ABC and $\Delta$ CDA :
(i) $\angle\ BCA\ =\ \angle DAC$
(ii) $\angle\ BAC\ =\ \angle DCA$
(iii) Side AC is common in both triangles.
Thus, by ASA congruence, we have :
$\Delta ABC\ \cong \ \Delta CDA$
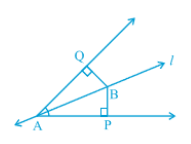
Answer:
In the given figure consider $\small \Delta APB$ and $\small \Delta AQB$ ,
(i) $\angle P\ =\ \angle Q$ (Right angle)
(ii) $\angle BAP\ =\ \angle BAQ$ (Since it is given that I is bisector)
(iii) Side AB is common in both triangles.
Thus, AAS congruence, we can write :
$\small \Delta APB\cong \Delta AQB$
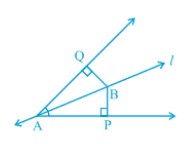
Answer:
In the previous part, we have proved that $\small \Delta APB\cong \Delta AQB$.
Thus, by c.p.c.t.. we can write :
$BP\ =\ BQ$
Thus, B is equidistant from the arms of angle A.
Question 6: In Fig, $\small AC=AE,AB=AD$ and $\small \angle BAD= \angle EAC$ . Show that $\small BC=DE$.
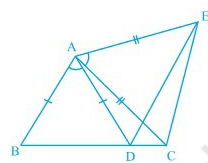
Answer:
From the given figure, the following result can be drawn:-
$\angle BAD\ =\ \angle EAC$
Adding $\angle DAC$ to both sides, we get :
$\angle BAD\ +\ \angle DAC\ =\ \angle EAC\ +\ \angle DAC$
$\angle BAC\ =\ \angle EAD$
Now consider $\Delta ABC$ and $\Delta ADE$ ,
(i) $AC\ =\ AE$ (Given)
(ii) $\angle BAC\ =\ \angle EAD$ (proved above)
(iii) $AB\ =\ AD$ (Given)
Thus, by SAS congruence, we can say that :
$\Delta ABC\ \cong \ \Delta ADE$
Hence by c.p.c.t., we can say that : $BC\ =\ DE$
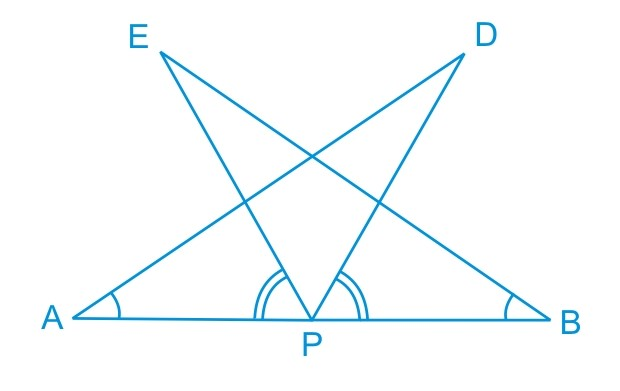
Answer:
From the figure, it is clear that :
$\angle EPA\ =\ \angle DPB$
Adding $\angle DPE$ on both sides, we get :
$\angle EPA\ +\ \angle DPE =\ \angle DPB\ +\ \angle DPE$
or $\angle DPA =\ \angle EPB$
Now, consider $\Delta DAP$ and $\Delta EBP$ :
(i) $\angle DPA =\ \angle EPB$ (Proved above)
(ii) $AP\ =\ BP$ (Since P is the midpoint of line AB)
(iii) $\small \angle BAD=\angle ABE$ (Given)
Hence, by ASA congruence, we can say that :
$\small \Delta DAP\cong \Delta EBP$
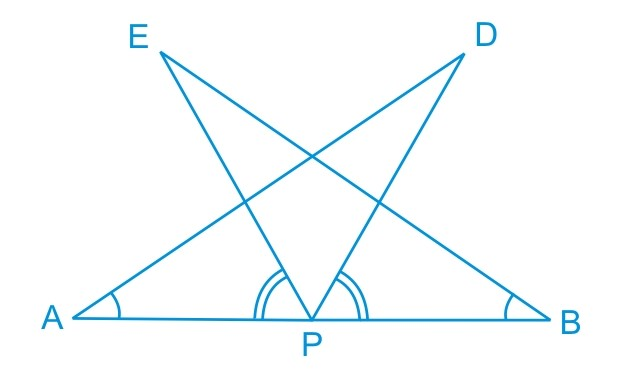
Answer:
In the previous part, we have proved that $\small \Delta DAP\cong \Delta EBP$.
Thus, by c.p.c.t., we can say that :
$\small AD=BE$
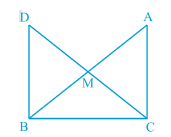
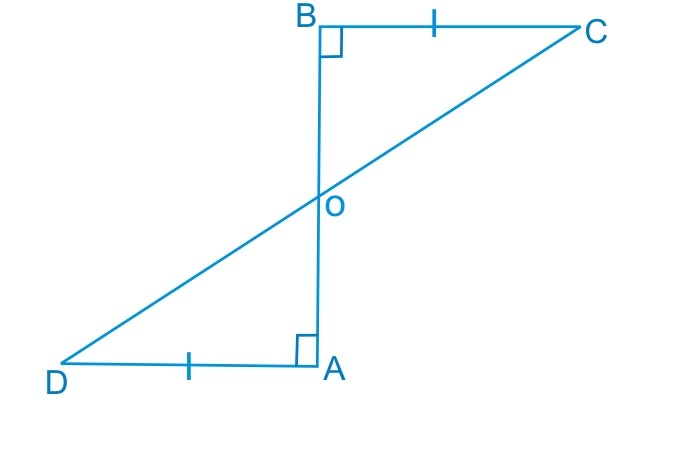
Answer:
Consider $\Delta AMC$ and $\Delta BMD$ ,
(i) $AM\ =\ BM$ (Since M is the mid-point)
(ii) $\angle CMA\ =\ \angle DMB$ (Vertically opposite angles are equal)
(iii) $CM\ =\ DM$ (Given)
Thus, by SAS congruency, we can conclude that :
$\small \Delta AMC\cong \Delta BMD$
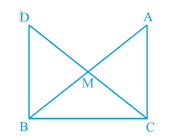
Answer:
In the previous part, we have proved that $\small \Delta AMC\cong \Delta BMD$
By c.p.c.t. we can say that : $\angle ACM\ =\ \angle BDM$
This implies that side AC is parallel to BD.
Thus we can write : $\angle ACB\ +\ \angle DBC\ =\ 180^{\circ}$ (Co-interior angles)
and, $90^{\circ}\ +\ \angle DBC\ =\ 180^{\circ}$
or $\angle DBC\ =\ 90^{\circ}$
Hence, $\small \angle DBC$ is a right angle.
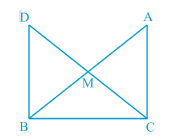
Answer:
Consider $\Delta DBC$ and $\Delta ACB$ ,
(i) $BC\ =\ BC$ (Common in both the triangles)
(ii) $\angle ACB\ =\ \angle DBC$ (Right angle)
(iii) $DB\ =\ AC$ (By c.p.c.t. from part (a) of the question.)
Thus, based on SAS congruence, we can conclude that :
$\small \Delta DBC\cong \Delta ACB$
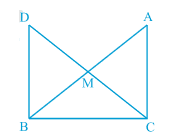
Answer:
In the previous part, we have proved that $\Delta DBC\ \cong \ \Delta ACB$.
Thus by c.p.c.t., we can write : $DC\ =\ AB$
$DM\ +\ CM\ =\ AM\ +\ BM$
or $CM\ +\ CM\ =\ AB$ (Since M is midpoint.)
or $\small CM=\frac{1}{2}AB$ .
Hence proved.
|
Triangles Class 9 Question Answers
Exercise: 7.2 Total Questions: 8
Page number: 97-98
|
Answer:
In the triangle ABC,
Since AB = AC, thus $\angle B\ =\ \angle C$
or $\frac{1}{2}\angle B\ =\ \frac{1}{2}\angle C$
or $\angle OBC\ =\ \angle OCB$ (Angles bisectors are equal)
Thus $\small OB=OC$ as sides opposite to equal are angles are also equal.
Answer:
Consider $\Delta AOB$ and $\Delta AOC$ ,
(i) $AB\ =\ AC$ (Given)
(ii) $AO\ =\ AO$ (Common in both the triangles)
(iii) $OB\ =\ OC$ (Proved in previous part)
Thus, by the SSS congruence rule, we can conclude that :
$\Delta AOB\ \cong \ \Delta AOC$
Now, by c.p.c.t.,
$\angle BAO\ =\ \angle CAO$
Hence, AO bisects $\angle A$.
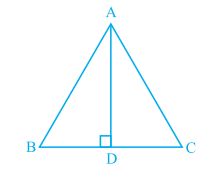
Answer:
Consider $\Delta$ ABD and $\Delta$ ADC,
(i) $AD\ =\ AD$ (Common in both the triangles)
(ii) $\angle ADB\ =\ \angle ADC$ (Right angle)
(iii) $BD\ =\ CD$ (Since AD is the bisector of BC)
Thus, by the SAS congruence axiom, we can state :
$\Delta ADB\ \cong \ \Delta ADC$
Hence, by c.p.c.t., we can say that : $\small AB=AC$
Thus $\Delta ABC$ is an isosceles triangle with AB and AC as equal sides.
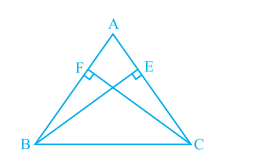
Answer:
Consider $\Delta AEB$ and $\Delta AFC$ ,
(i) $\angle A$ is common to both triangles.
(ii) $\angle AEB\ =\ \angle AFC$ (Right angles)
(iii) $AB\ =\ AC$ (Given)
Thus, by the AAS congruence axiom, we can conclude that :
$\Delta AEB\ \cong \Delta AFC$
Now, by c.p.c.t. we can say : $BE\ =\ CF$
Hence, these altitudes are equal.
Question 4: (i) ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that $\small \Delta ABE \cong \Delta ACF$
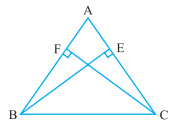
Answer:
Consider $\Delta ABE$ and $\Delta ACF$ ,
(i) $\angle A$ is common to both triangles.
(ii) $\angle AEB\ =\ \angle AFC$ (Right angles)
(iii) $BE\ =\ CF$ (Given)
Thus, by AAS congruence, we can say that :
$\small \Delta ABE \cong \Delta ACF$
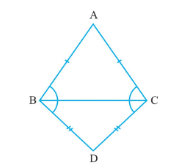
Question 4: (ii) ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig.). Show that $\small AB=AC$, i.e., ABC is an isosceles triangle.
Answer:
From the previous part of the question, we found out that: $\Delta ABE\ \cong \Delta ACF$
Now, by c.p.c.t. we can say that : $AB\ =\ AC$
Hence, $\Delta \ ABC$ is an isosceles triangle.
Answer:
Consider $\Delta ABD$ and $\Delta ACD$ ,
(i) $AD\ =\ AD$ (Common in both the triangles)
(ii) $AB\ =\ AC$ (Sides of isosceles triangle)
(iii) $BD\ =\ CD$ (Sides of isosceles triangle)
Thus, by SSS congruency, we can conclude that :
$\small \angle ABD\ \cong \ \angle ACD$
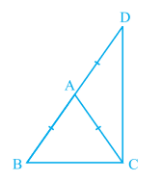
Answer:
Consider $\Delta$ ABC,
It is given that AB = AC
So, $\angle ACB = \angle ABC$ (Since angles opposite to the equal sides are equal.)
Similarly in $\Delta$ ACD,
We have AD = AB
and $\angle ADC = \angle ACD$
So,
$\angle CAB + \angle ACB + \angle ABC = 180^{\circ}$
$\angle CAB\ +\ 2\angle ACB = 180^{\circ}$
or $\angle CAB\ = 180^{\circ}\ -\ 2\angle ACB$ ...........................(i)
And in $\Delta$ ADC,
$\angle CAD\ = 180^{\circ}\ -\ 2\angle ACD$ ..............................(ii)
Adding (i) and (ii), we get :
$\angle CAB\ +\ \angle CAD\ = 360^{\circ}\ -\ 2\angle ACD\ -\ 2\angle ACB$
or $180^{\circ}\ = 360^{\circ}\ -\ 2\angle ACD\ -\ 2\angle ACB$
and $\angle BCD\ =\ 90^{\circ}$
Answer:
In the triangle ABC, sides AB and AC are equal.
We know that angles opposite to equal sides are also equal.
Thus, $\angle B\ =\ \angle C$
Also, the sum of the interior angles of a triangle is $180^{\circ}$
So, we have :
$\angle A\ +\ \angle B\ +\ \angle C\ =\ 180^{\circ}$
or $90^{\circ} +\ 2\angle B\ =\ 180^{\circ}$
or $\angle B\ =\ 45^{\circ}$
Hence, $\angle B\ =\ \angle C\ =\ 45^{\circ}$
Question 8: Show that the angles of an equilateral triangle are $\small 60^{\circ}$ each.
Answer:
Consider a triangle ABC that has all sides equal.
We know that angles opposite to equal sides are equal.
Thus we can write : $\angle A\ =\ \angle B\ =\ \angle C$
Also, the sum of the interior angles of a triangle is $180 ^{\circ}$.
Hence, $\angle A\ +\ \angle B\ +\ \angle C\ =\ 180^{\circ}$
or $3\angle A\ =\ 180^{\circ}$
or $\angle A\ =\ 60^{\circ}$
So, all the angles of the equilateral triangle are equal ( $60^{\circ}$ ).
|
Triangles Class 9 Question Answers
Exercise: 7.3 Total Questions: 5
Page number: 102
|
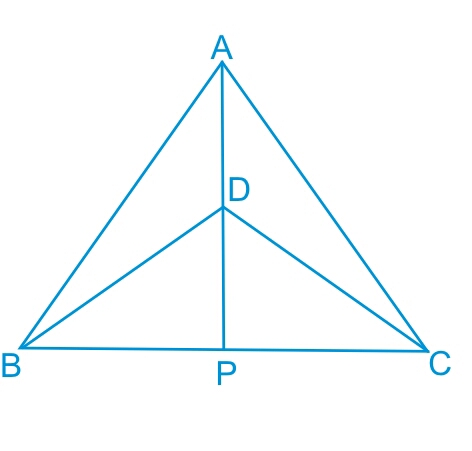
Answer:
Consider $\Delta ABD$ and $\Delta ACD$ ,
(i) $AD\ =\ AD$ (Common)
(ii) $AB\ =\ AC$ (Isosceles triangle)
(iii) $BD\ =\ CD$ (Isosceles triangle)
Thus, by SSS congruency, we can conclude that :
$\small \Delta ABD\cong \Delta ACD$
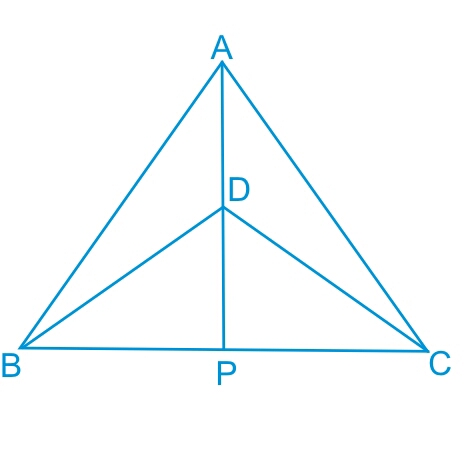
Answer:
Consider $\Delta ABP$ and $\Delta ACP$,
(i) $AP$ is the common side in both triangles.
(ii) $\angle PAB\ =\ \angle PAC$ (This is obtained from the c.p.c.t. as proved in the previous part.)
(iii) $AB\ =\ AC$ (Isosceles triangles)
Thus, by the SAS axiom, we can conclude that :
$\small \Delta ABP \cong \Delta ACP$
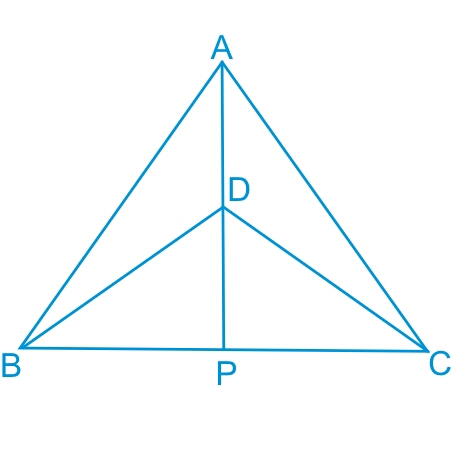
Answer:
In the first part, we have proved that $\small \Delta ABD\cong \Delta ACD$
So, by c.p.c.t. $\angle PAB\ =\ \angle PAC$ .
Hence, AP bisects $\angle A$.
Now consider $\Delta BPD$ and $\Delta CPD$ ,
(i) $PD\ =\ PD$ (Common)
(ii) $BD\ =\ CD$ (Isosceles triangle)
(iii) $BP\ =\ CP$ (by c.p.c.t. from the part (b))
Thus, by SSS congruency, we have :
$\Delta BPD\ \cong \ \Delta CPD$
Hence by c.p.c.t. we have : $\angle BDP\ =\ \angle CDP$
or AP bisects $\angle D$ .
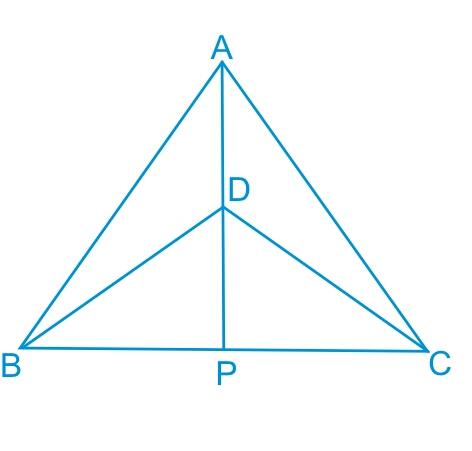
Answer:
In the previous part, we have proved that $\Delta BPD\ \cong \ \Delta CPD$.
Thus by c.p.c.t. we can say that : $\angle BPD\ =\ \angle CPD$
Also, $BP\ =\ CP$
Since BC is a straight line, thus : $\angle BPD\ +\ \angle CPD\ =\ 180^{\circ}$
or $2\angle BPD\ =\ 180^{\circ}$
or $\angle BPD\ =\ 90^{\circ}$
Hence, it is clear that AP is a perpendicular bisector of line BC.
Question 2: (i) AD is an altitude of an isosceles triangle ABC in which $\small AB=AC$. Show that AD bisects BC
Answer:
Consider $\Delta ABD$ and $\Delta ACD$ ,
(i) $AB\ =\ AC$ (Given)
(ii) $AD\ =\ AD$ (Common in both triangles)
(iii) $\angle ADB\ =\ \angle ADC\ =\ 90^{\circ}$
Thus, by the RHS axiom, we can conclude that :
$\Delta ABD\ \cong \ \Delta ACD$
Hence, by c.p.c.t., we can say that: $BD\ =\ CD$ or AD bisects BC.
Question 2: (ii) AD is an altitude of an isosceles triangle ABC in which $\small AB=AC$. Show that AD bisects $\small \angle A$
Answer:
In the previous part of the question, we have proved that $\Delta ABD\ \cong \ \Delta ACD$
Thus by c.p.c.t., we can write :
$\angle BAD\ =\ \angle CAD$
Hence, $AD$ bisects $\angle A$ .
(i) $\small \Delta ABM \cong \Delta PQN$
(ii) $\small \Delta ABC \cong \Delta PQR$
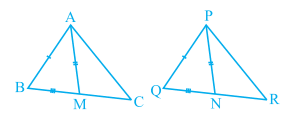
Answer:
(i) From the figure, we can say that :
$BC\ =\ QR$
or $\frac{1}{2}BC\ =\ \frac{1}{2}QR$
or $BM\ =\ QN$
Now, consider $\Delta ABM$ and $\Delta PQN$ ,
(a) $AM\ =\ PN$ (Given)
(b) $AB\ =\ PQ$ (Given)
(c) $BM\ =\ QN$ (Prove above)
Thus, by the SSS congruence rule, we can conclude that :
$\small \Delta ABM \cong \Delta PQN$
(ii) Consider $\Delta ABC$ and $\Delta PQR$ :
(a) $AB\ =\ PQ$ (Given)
(b) $\angle ABC\ =\ \angle PQR$ (by c.p.c.t. from the above proof)
(c) $BC\ =\ QR$ (Given)
Thus, by the SAS congruence rule,
$\small \Delta ABC \cong \Delta PQR$
Answer:
Using the given conditions, consider $\Delta BEC$ and $\Delta CFB$ ,
(i) $\angle BEC\ =\ \angle CFB$ (Right angle)
(ii) $BC\ =\ BC$ (Common in both the triangles)
(iii) $BE\ =\ CF$ (Given that altitudes are of the same length. )
Thus, by the RHS axiom, we can say that: $\Delta BEC\ \cong \Delta CFB$
Hence by c.p.c.t., $\angle B\ =\ \angle C$
And thus $AB\ =\ AC$ (sides opposite to equal angles are also equal).
Thus, ABC is an isosceles triangle.
Answer:
Consider $\Delta ABP$ and $\Delta ACP$ ,
(i) $\angle APB\ =\ \angle APC\ =\ 90^{\circ}$ (Since it is given that AP is the altitude.)
(ii) $AB\ =\ AC$ (Isosceles triangle)
(iii) $AP\ =\ AP$ (Common in both triangles)
Thus, by the RHS axiom, we can conclude that :
$\Delta ABP\ \cong \Delta ACP$
Now, by c.p.c.t., we can say that :
$\angle B\ =\ \angle C$
Triangles Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Triangles Class 9 Maths Chapter 7 are provided in the links below.
Class 9 Maths NCERT Chapter 7 Solutions: Extra Questions
Question 1: In triangle ABC, AB = AC and $\angle B$ = 50°. Find $\angle A$.
Answer:
Given AB = AC, it is an isosceles triangle
Therefore, $\angle B$ = $\angle C$ = 50°
Now, using the angle sum property:
$\angle A + \angle B + \angle C$ = 180°
$\Rightarrow \angle A$ + 50° + 50° = 180°
$\Rightarrow \angle A$ = 80°
Question 2:
$\triangle \mathrm{MNO}$ is similar to $\triangle \mathrm{STU}$. Perimeters of $\triangle \mathrm{MNO}$ and $\triangle \mathrm{STU}$ are 80 cm and 200 cm, respectively. If ON = 25 cm, then what is the length of TU?
Answer:
The perimeter of $\triangle$MNO = 80 cm
The perimeter of $\triangle$STU = 200 cm
$\triangle$MNO is similar to $\triangle$STU, if ON = 25 cm
$\frac{\text{Perimeter of $\triangle$MNO}}{\text{Perimeter of $\triangle$STU}} = \frac{\text{ON}}{\text{TU}}$
⇒ $\frac{80}{200} = \frac{25}{\text{TU}}$
⇒ TU = $25\times{\frac{200}{80}}$
$\therefore$ TU = 62.5 cm
Hence, the correct answer is 62.5 cm.
Question 3:
In $\triangle XYZ$, points P, Q, and R are points on the sides XY, YZ, and XZ, respectively $\angle YXZ = 50^\circ$, XR = PR, ZR = QR, and $\angle RQZ = 80^\circ$. What is the value of $\angle PRQ$?
Answer:
In $\triangle XPR$
$\angle PXR = 50^\circ$
Since XR = PR, the triangle is isosceles.
$\angle$XPR = $\angle$PXR = 50$^\circ$
⇒ $\angle XRP = 180^\circ-50^\circ-50^\circ= 80^\circ$
Since ZR = QR, the triangle is isosceles.
Similarly,
$\angle RQZ = \angle RZQ = 80^\circ$
⇒ $\angle QRZ = 180^\circ- 80^\circ- 80^\circ = 20^\circ$
Now, $\angle PRQ = 180^\circ - \angle RQZ - \angle XPR$
$⇒\angle PRQ = 180^\circ-20^\circ- 80^\circ=80^\circ$
Hence, the correct answer is $80^\circ$.
Question 4:
In $\triangle \mathrm{STU}, \mathrm{SX}$ is the median on $\mathrm{TU}$. If $\mathrm{SX}=\mathrm{TX}$, then what is the value of $\angle \mathrm{TSU}$?
Answer:
In $\triangle$STU, SX is the median.
So, TX = XU (median property)
SX = TX (given)
So, $\triangle$STX is an isosceles triangle.
Let $\angle$STX = $\angle$TSX = $\theta$
⇒ $\angle$SXU = $2\theta$ (exterior angle)
Similarly in $\triangle$SXU,
SX = XU
$\triangle$SXU is an isosceles triangle.
Let $\angle$SUX = $\angle$USX = $\alpha$
⇒ $\angle$SXT = $2\alpha$ (exterior angle)
Now,
$2\theta + 2\alpha = 180° $ (Linear pair)
$⇒\theta + \alpha = 90°$
So, $\angle$TSU $= \theta +\alpha = 90°$
Hence, the correct answer is 90°.
Question 5:
Let ABC be a triangle. If the mid-points of AB, BC and AC are D, E and F, respectively, then DEF is NOT congruent to _____.
1. BDE
2. ABC
3. ECF
4. ADF
Answer:
By midpoint theorem, $\triangle D E F \sim \triangle A B C$
and $\triangle D E F =\frac14 \triangle A B C$
Since $\triangle D E F$ is smaller than $\triangle A B C$, they are not congruent.
Also, according to the Midpoint Theorem, $\triangle B D E, \triangle E C F$, and $\triangle A D F$ are congruent to $\triangle D E F$ because they all contain two sides that are halves of the original triangle's sides.
Hence, the correct answer is ABC.
Triangles Class 9 Chapter 7: Topics
The topics discussed in the NCERT Solutions for Class 9 Maths Chapter 7 Triangles are:
- Introduction
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Some Properties of a Triangle
- More Criteria for the Congruence of Triangles
NCERT Triangles Class 9 Solutions: Important Formulae And Points
Congruence:
-
Congruent refers to figures that are identical in all aspects, including their shapes and sizes. For example, two circles with the same radius or two squares with the same side lengths are considered congruent.
Congruent Triangles:
-
Two triangles are considered congruent if and only if one of them can be superimposed (placed or overlaid) over the other in such a way that they entirely cover each other.
Properties of Congruent Triangles
-
Corresponding sides are equal.
-
Corresponding angles are equal.
-
The areas of congruent triangles are the same.
-
The perimeters of congruent triangles are the same.
Congruence Rules for Triangles:
-
Side-Angle-Side (SAS) Congruence:
-
Angle-Side-Angle (ASA) Congruence:
-
Angle-Angle-Side (AAS) Congruence:.
-
Side-Side-Side (SSS) Congruence:
-
Right-Angle Hypotenuse Side (RHS) Congruence:
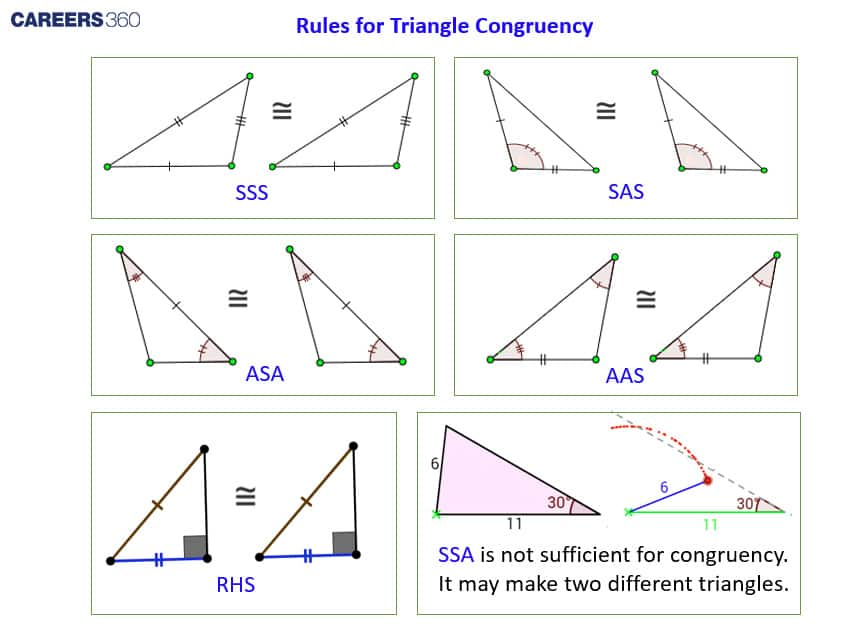
What is CPCT?
CPCT stands for "Corresponding Parts of Congruent Triangles." It is a principle that states that if two or more triangles are congruent, then all of their corresponding parts (sides and angles) are also congruent.
Approach to Solve Questions of Triangles Class 9
Using these approaches, students can tackle the Triangles Class 9 Chapter 7 Question Answers with greater confidence.
- Understand triangle classification: Master the classification of triangles using side and angle properties, such as scalene, isosceles, equilateral, in addition to acute, right and obtuse.
- Apply the angle sum property: The total measurement of interior triangle angles always amounts to 180° to find missing angles.
- Use congruence rules: Apply the SSS, SAS, ASA, RHS and AAS master criteria to prove triangle congruence, together with solving related problems.
- Relate properties of isosceles and equilateral triangles: Theorems demonstrate that when two triangle sides are equal, the opposing angles match in size, and when two angles have matching measures, the connected sides are equivalent in length.
- Explore inequalities in triangles: Explain the relationship between angles and side lengths, as well as the principle that the two side lengths combined always measure more than the third side.
- Practice reasoning-based proofs: Students need to complete statement-reason questions involving triangle problems by implementing logical sequences and theorem usage.
Why are Class 9 Maths Chapter 7 Triangles Question Answers Important?
Triangles are one of the most important shapes in geometry. This chapter teaches how to compare triangles, understand their properties, and solve problems using these concepts. These Class 9 Maths Chapter 7 Triangles question answers help students practise these ideas clearly. Here are some more points on why these question answers are important:
- These solutions help you learn how to check if two triangles are congruent using different criteria.
- These question answers make it easier to understand and apply the properties of triangles in problems.
- These Class 9 Maths Chapter 7 Triangles question answers prepare us for higher classes where we will study advanced geometry, including quadrilaterals and coordinate geometry.
NCERT Solutions for Class 9 Chapter Wise
We at Careers360 compiled all the NCERT class 9 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and NCERT Syllabus
Given below are direct links to the NCERT Books and the latest NCERT Syllabus for your convenience.
Frequently Asked Questions (FAQs)
Q: What are the important topics in chapter 7 maths class 9?
A:
Topics in Maths Chapter 7 Class 9 include:
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Some Properties of a Triangle
- More Criteria for the Congruence of Triangles
Q: What is the Pythagoras theorem?
A:
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides:
c² = a² + b²
where,
c = hypotenuse,
a = base and
b = perpendicular
Q: How many exercises are there in NCERT Class 9 Maths Chapter 7?
A:
There are 3 exercises, covering conceptual questions, numerical problems, and proofs based on congruence and triangle properties.
Q: Where can I find free NCERT Solutions for Class 9 Maths Chapter 7?
A:
Free NCERT Triangles Class 9 solutions are available online on many educational platforms, such as Careers360, in PDF and web formats, covering all exercises with clear, step-by-step explanations.
Q: What is triangle congruence?
A:
Two triangles are congruent if all their corresponding sides and angles are equal.
Congruence can be proved using the criteria:
SSS (Side-Side-Side)
SAS (Side-Angle-Side)
ASA (Angle-Side-Angle)
RHS (Right-angle-Hypotenuse-Side)
Q: Where are triangles used in real life?
A:
Triangles are used in many fields, such as:
Construction and architecture
Engineering designs
Navigation and surveying
Graphic design and art
Q: What are the triangle inequalities?
A:
Triangle inequalities are:
Any side of a triangle is less than the sum of the other two sides.
Any side of a triangle is greater than the difference of the other two sides.
Q: What are some key properties of triangles?
A:
Some of the key properties of triangles are:
The sum of the angles of a triangle is 180°.
The sum of the lengths of any two sides is greater than the third side.
The difference in lengths of any two sides is less than the third side.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters