NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

A quadrilateral is a geometrical shape that has four sides and four corners. The sides of quadrilaterals are also called edges, and their corners are called vertices. It is a closed shape with four angles; quadrilaterals are also called polygons. In our daily life, many objects are similar to quadrilaterals. Quadrilaterals are used in graphic design, logos, architecture, like house blueprints, windows, floors, walls, and in everyday objects like paper, electronic devices, picture frames, stationery items, etc.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

1. NCERT Class 9 Maths Chapter 8 Quadrilaterals: Notes
2. Class 9 Chapter Wise Notes
3. NCERT Solutions for Class 9
4. NCERT Exemplar Solutions for Class 9
5. NCERT Books and Syllabus

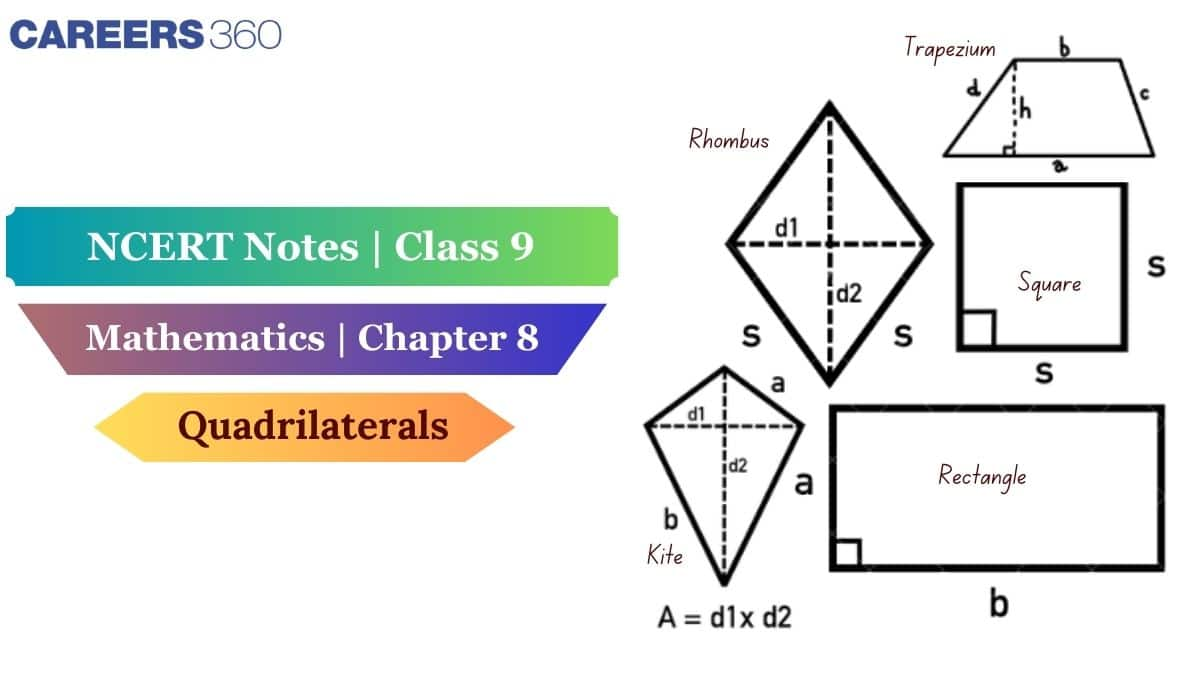
These notes cover different types of quadrilaterals and theorems related to opposite sides of parallelograms, properties of diagonals, diagonals of the rhombus, etc. CBSE Class 9 chapter includes examples for the given topics as required. NCERT class 9th maths notes include all the definitions, formulas, and examples and all related theorems. Students can download the NCERT notes according to their subjects and standard, which will help to understand all the required concepts in a single place.

NCERT Class 9 Maths Chapter 8 Quadrilaterals: Notes

Quadrilateral: The quadrilateral combines two Latin words, "quadri" and "latus"; quadri means a variant of four and latus means sides. So, the word quadrilateral implies that a shape has four sides.

Types of Quadrilaterals:

There are the following types of quadrilaterals -
1. Parallelogram
2. Trapezium
3. Rectangle
4. Square
5. Rhombus
6. Kite

Parallelogram: A parallelogram is a quadrilateral in which opposite sides are parallel and equal to each other.

Trapezium: A quadrilateral in which any two sides are parallel is called a trapezium.
Theorem: The opposite sides of a parallelogram are equal.

Rectangle: A quadrilateral in which two opposite sides are equal as well as well and all the angles are right angles.

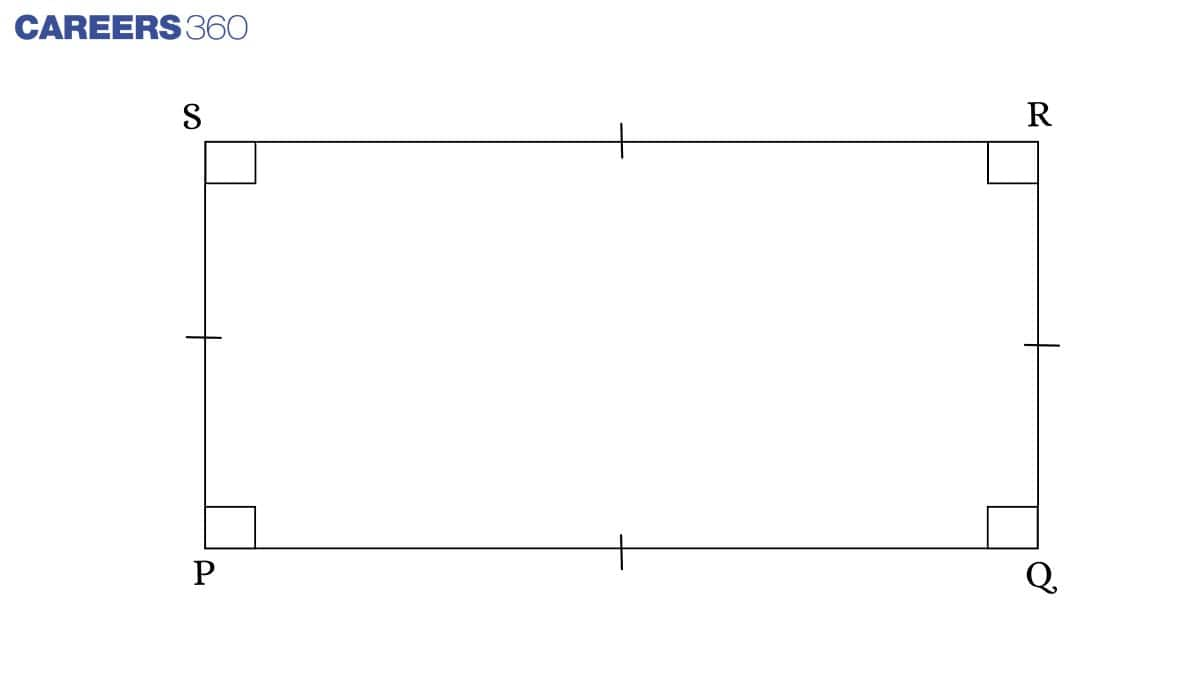
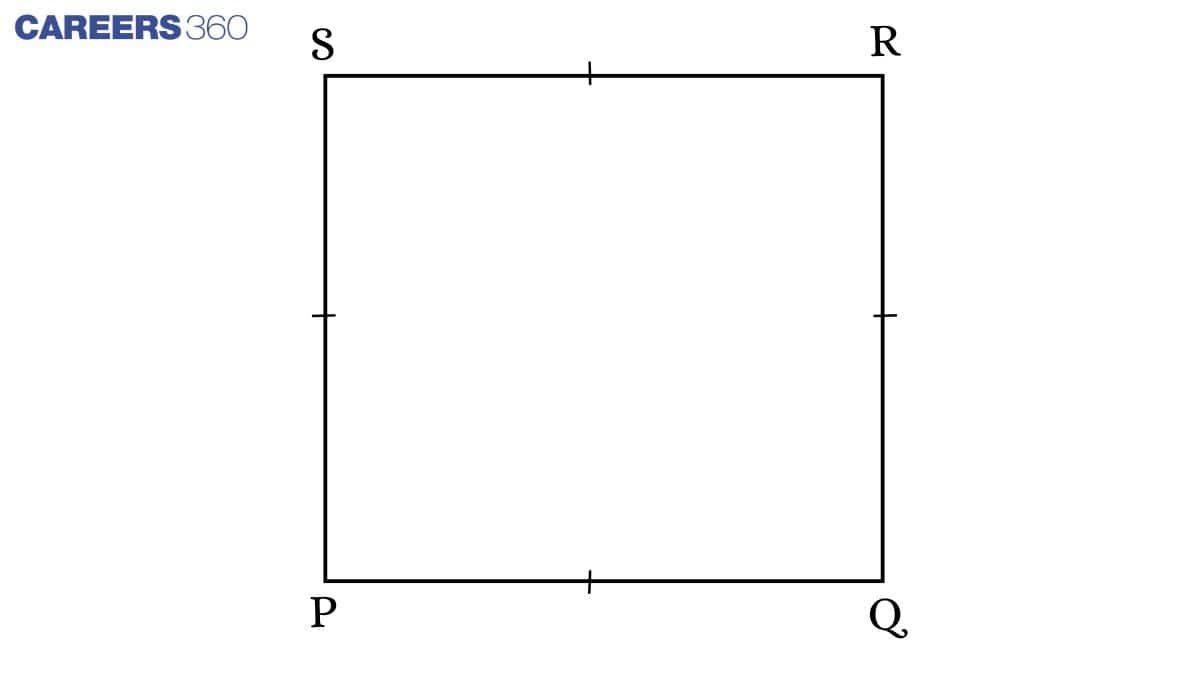
Square: It is a type of parallelogram in which all the angles are right angles and all sides are equal.

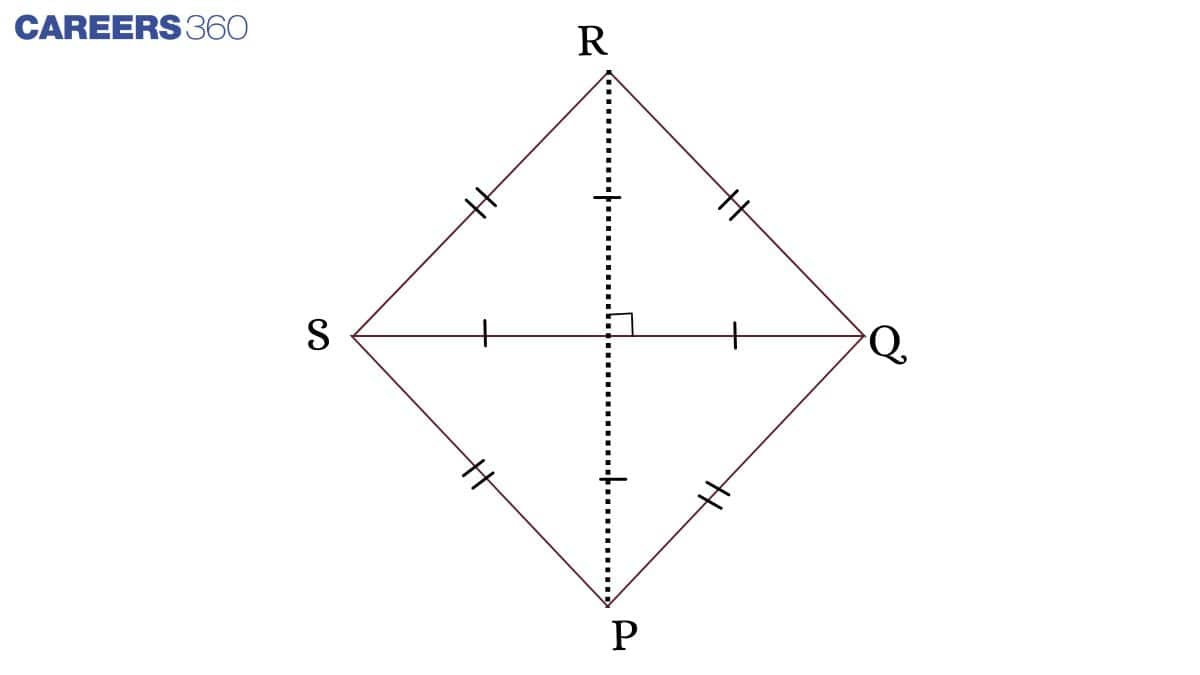
Rhombus: A rhombus is a parallelogram in which all the sides are equal and the diagonals perpendicularly bisect each other.

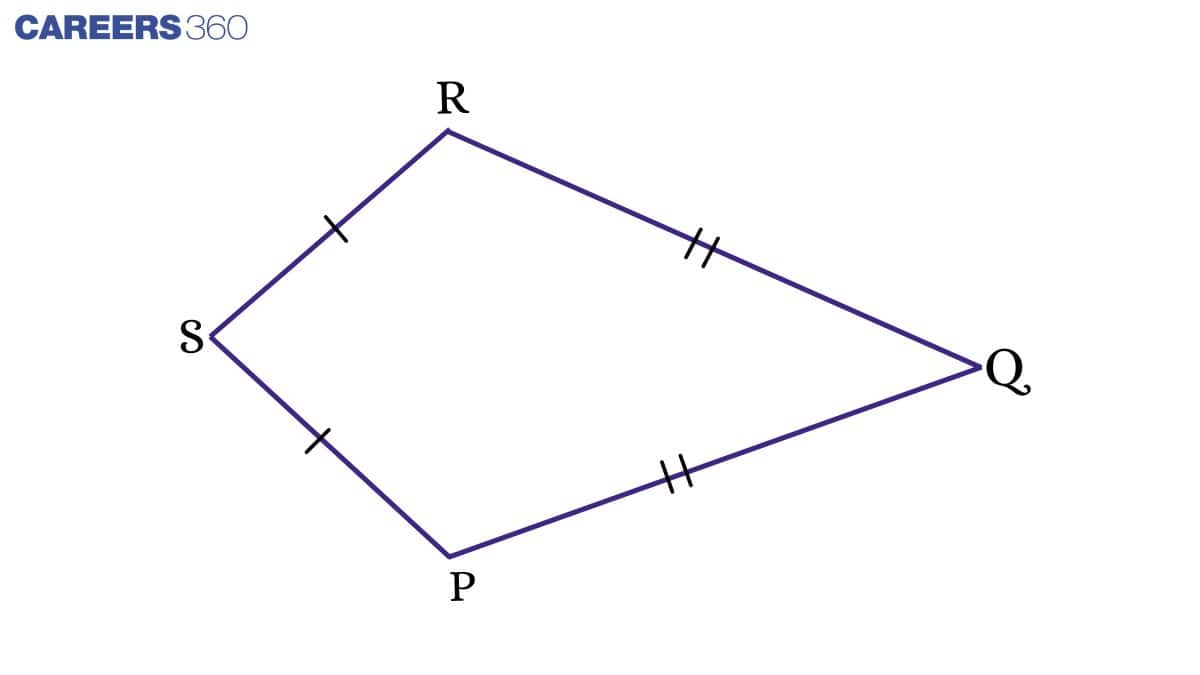
Kite: A quadrilateral in which adjacent sides are equal is called a kite.

Theorem: In a parallelogram, opposite sides are equal.

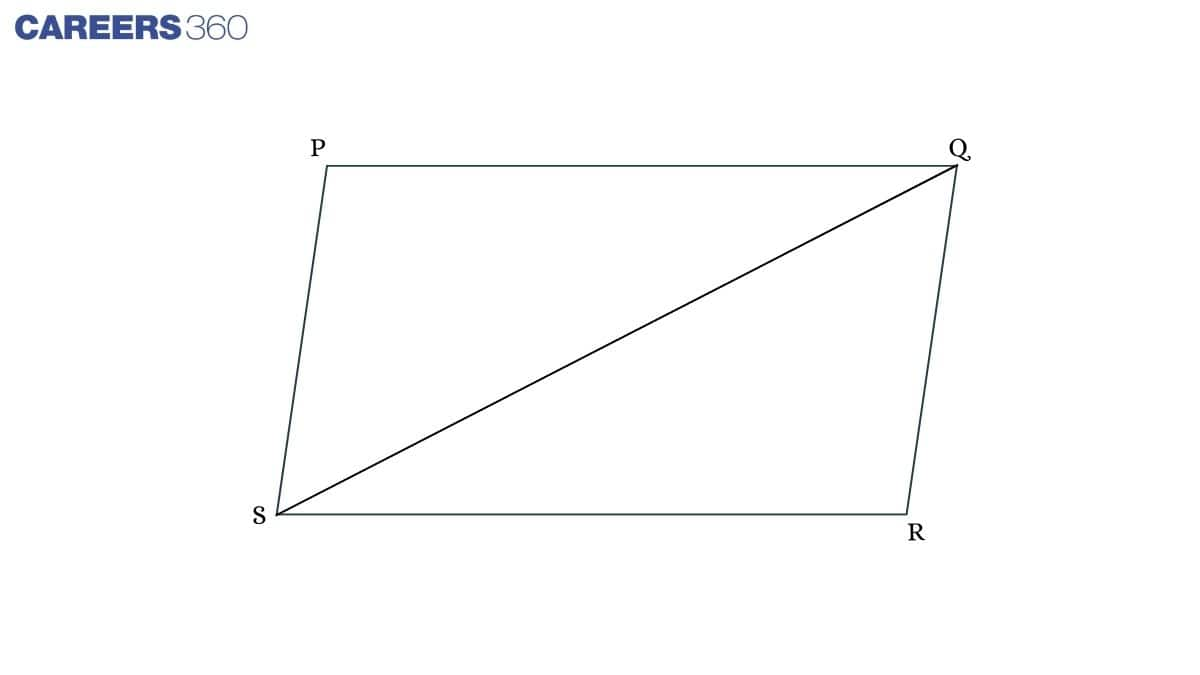
Let there be a diagonal that joins Q and S.In ΔPQS and ΔQRS
∠PQS = ∠QSR (Alternate angles)
QS = QS (Common)
∠PSQ = ∠RQS (Alternate angles)
ΔPQS≅ΔQRS (ASA rule)
Hence, PQ = RS and PS = QR.

Theorem: In a parallelogram, opposite angles are equal.

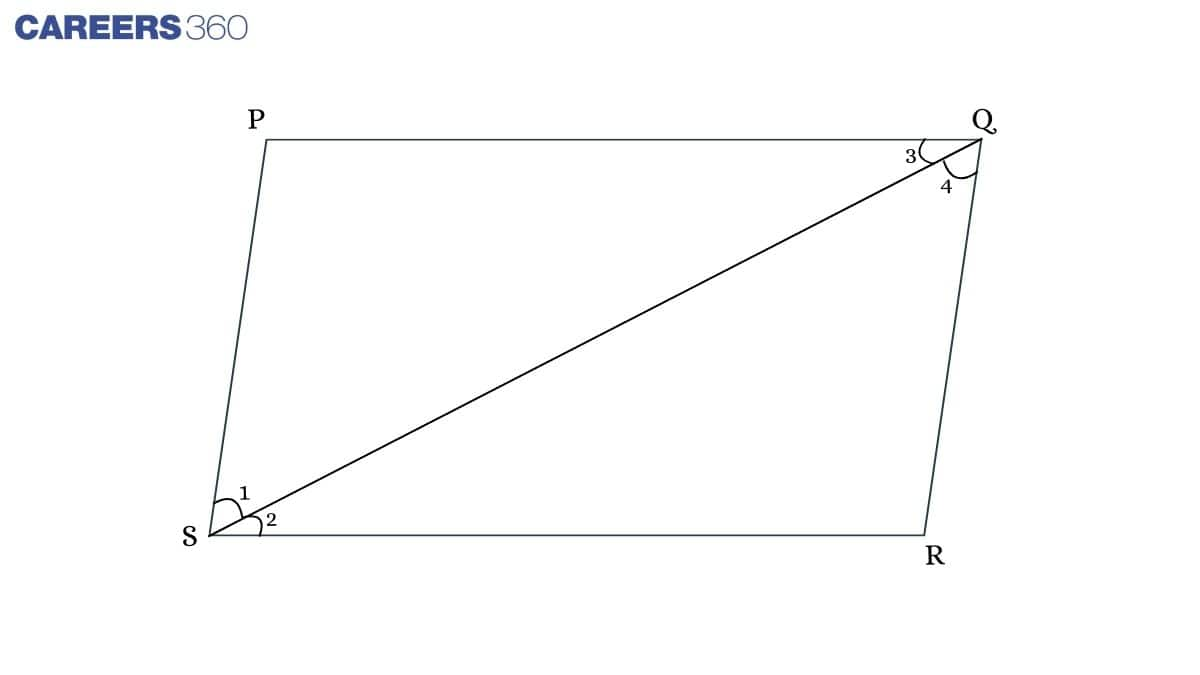
In parallelogram PQRS∠1 = ∠4 (PS || QR) .... (1)
∠2 = ∠3 (PQ || SR) ..... (2)
After adding equations (1) and (2), we get,
∠1 + ∠2 = ∠4 + ∠3
∠PSR = ∠PQR
Similarly, ∠QPS = ∠QRS

Theorem: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

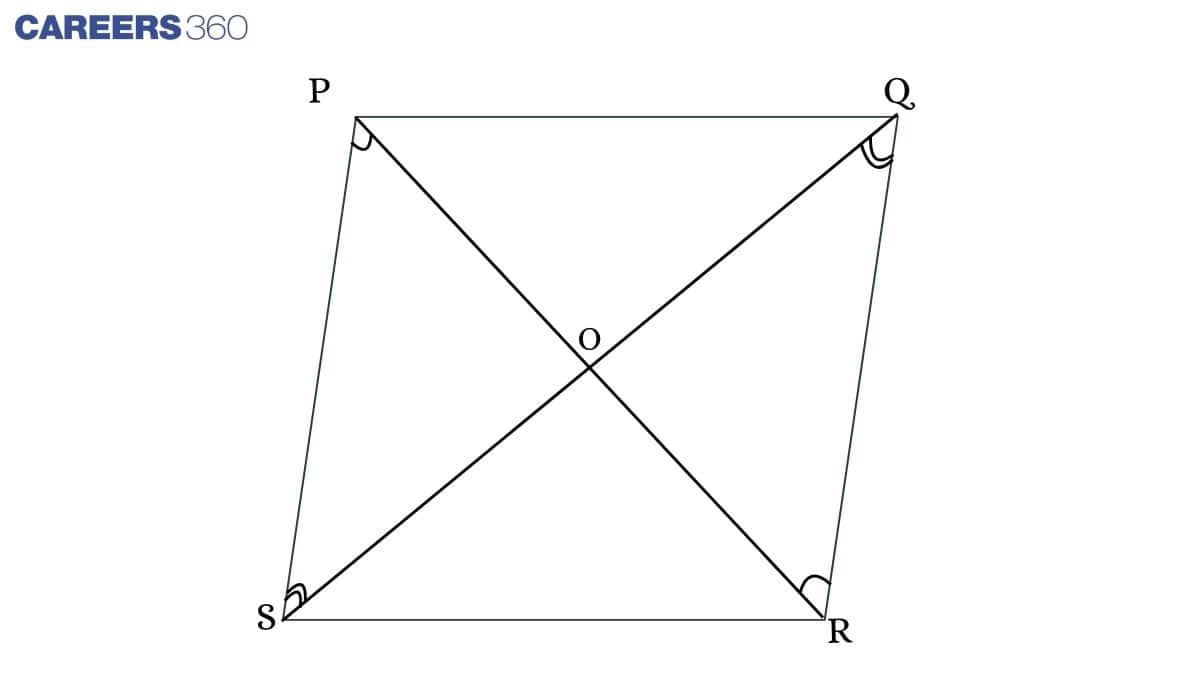
In ΔQOR and ΔPOS,
∠SPO = ∠ORQ (Alternate angles)
∠PSO = ∠OQR (Alternate angles)
PS = QR (Opposite sides of parallelogram)
ΔQOR ≅ ΔPOS (AAS rule)
Therefore, PO = OR and SO = OQ

Theorem: The diagonal of a parallelogram divides it into two congruent triangles.

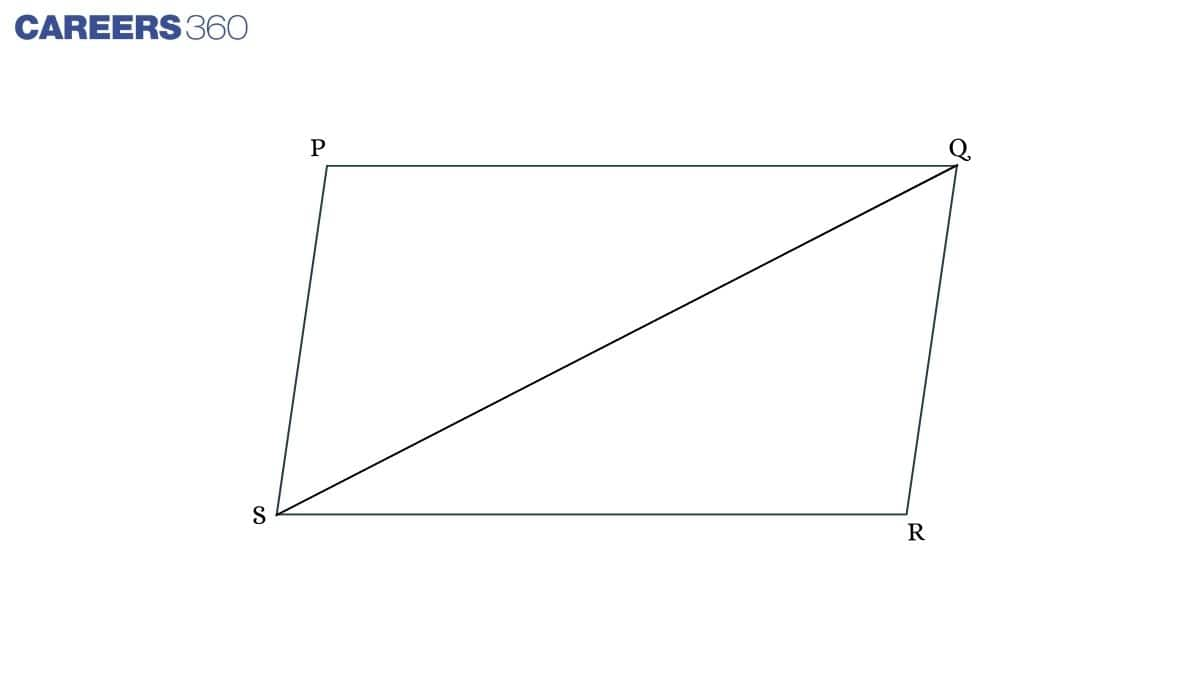
In ΔPQS and ΔQRS,
PQ = RS (Opposite sides of parallelogram)
PS = QR (Opposite sides of a parallelogram)
QS = QS (Common side in both triangles)
ΔPQS ≅ ΔQRS (By SSS rule)

Theorem: The diagonals of a rhombus bisect each other at right angles.

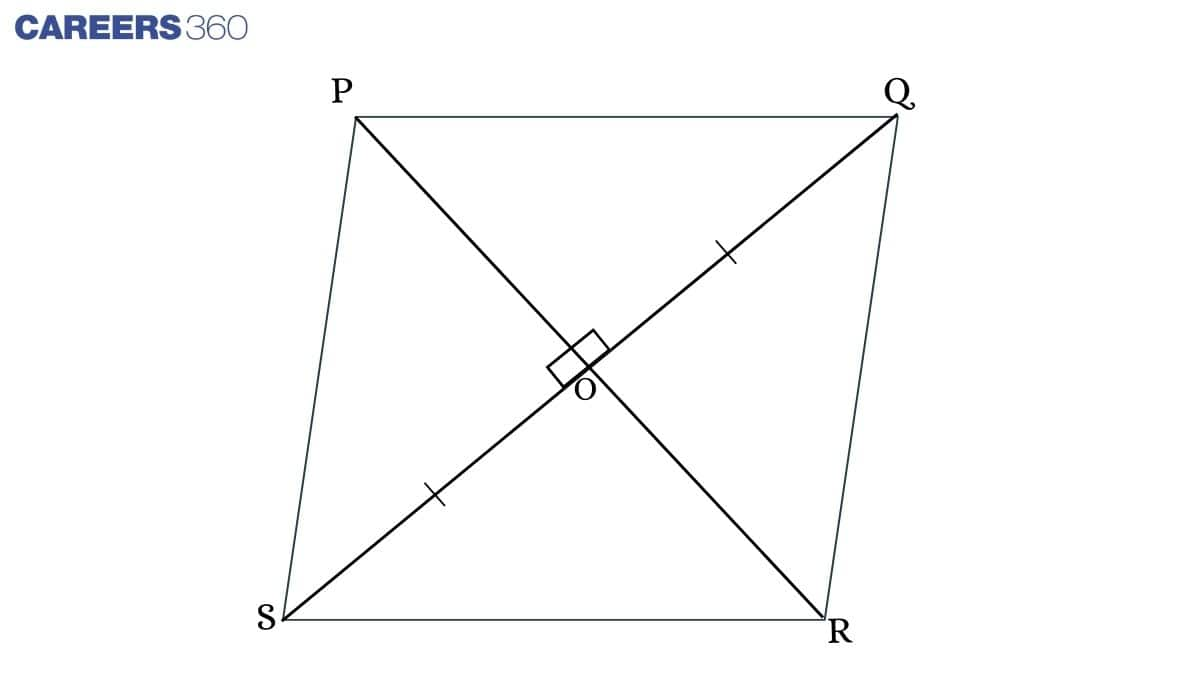
In ΔSOP and ΔPOQ,
PS = PQ (Adjacent sides of a rhombus)
PO = PO (Common side)
SO = OQ (Diagonals of a parallelogram that bisect each other)
ΔSOP ≅ΔPOQ (By SSS rule)
Therefore, ∠SOP =∠POQ ... (1)
∠SOP +∠POQ =180° (∵ Angle in a straight line is 180°)
From equation (1),
∠SOP +∠SOP =180°
∠SOP = 90°
Similarly, ∠SOP = ∠POQ = 90°

Theorem: The diagonals of a rectangle bisect each other and are equal.

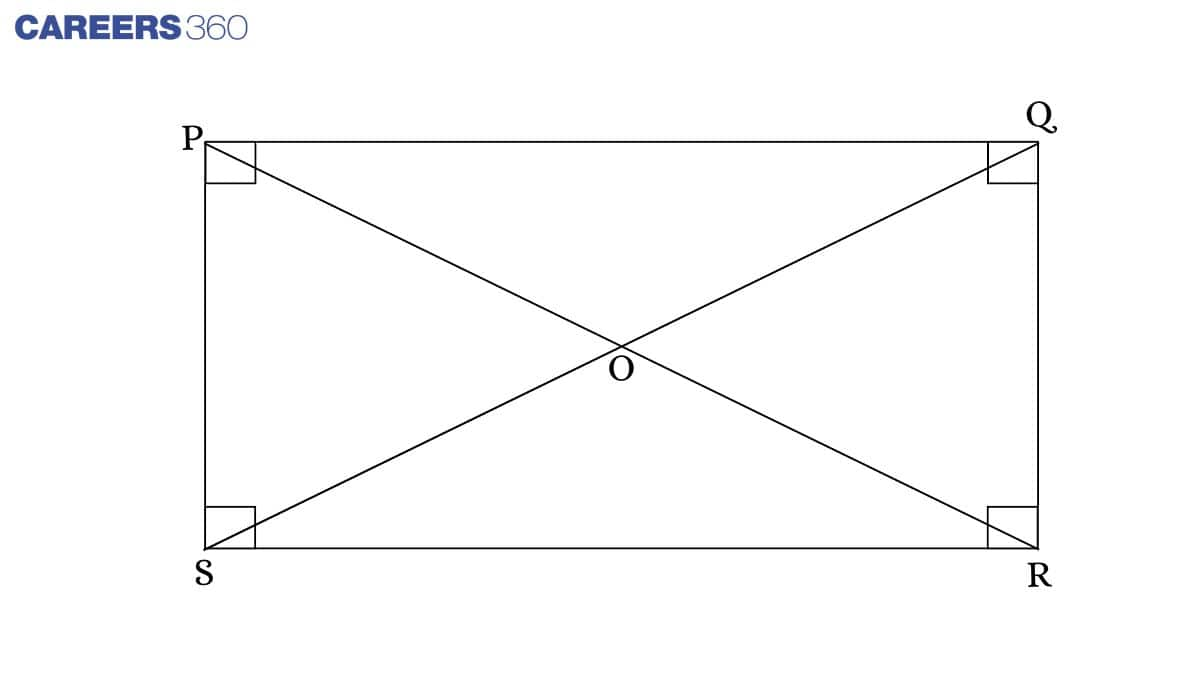
In ΔPSQ and ΔRSQ,
PS = QR (Opposite sides of a rectangle)
PQ = SR (Opposite sides of a rectangle)
∠SPQ = ∠SRQ (Angles of rectangle are 90°)
ΔPSQ ≅ΔRSQ (By SAS rule)
∴SQ = PR (Corresponding parts of congruent triangles)
Now, in ΔPOS and ΔQOR,
∠OSP = ∠OQR (∵ PS||QR)
∠SPO=∠ORQ (∵ AD||BC)
PS = QR (Opposite sides of a rectangle)
ΔPOS ≅ΔQOR (By ASA rule)
Therefore, SO = OQ (Corresponding parts of congruent triangles)
Similarly, we can prove PO = OR.

Theorem: The diagonals of a square bisect each other at right angles and are equal.

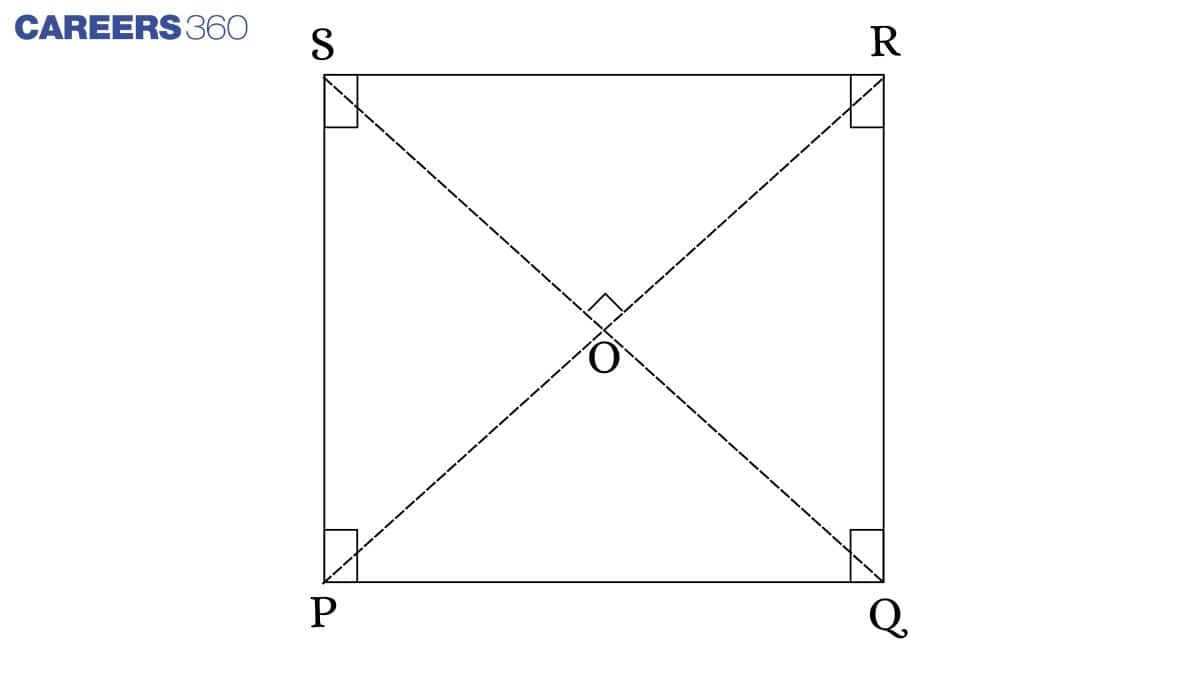
In ΔPRS and ΔPQR,
PS = QR (Opposite sides of a Square)
RS = PQ (Opposite sides of a Square)
PR = PR (Common side)
∠PQR =∠PSR (Each angle of the square is 90°)
ΔPRS ≅ΔPQR (By SAS rule)
Therefore, PR = SQ (Corresponding parts of congruent triangles)
Now in ΔPOS and ΔPOQ,
PS = RQ (Opposite sides of a square)
∠PSO =∠OQR (∵ PS || RQ)
∠SPO =∠ORQ (∵ SR || PQ)
ΔPOS ≅ΔPOQ (By ASA rule)
∴PO = OR (Corresponding parts of congruent triangles)
Similarly, we can prove SO = OQ
In ΔPSO and ΔPOQ,
OP = OP (Common side)
SO = OQ (Already proved)
PS = PQ (Side of square)
ΔPSO ≅ΔPOQ (By SSS rule)
∴∠POQ = ∠POS (Corresponding parts of congruent triangles)
Now, ∠POS +∠POQ =180° (Angle in a line is equal to 180°)
∴∠POS = ∠POQ = 90°

The Mid-Point Theorem

The line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half of the third side.

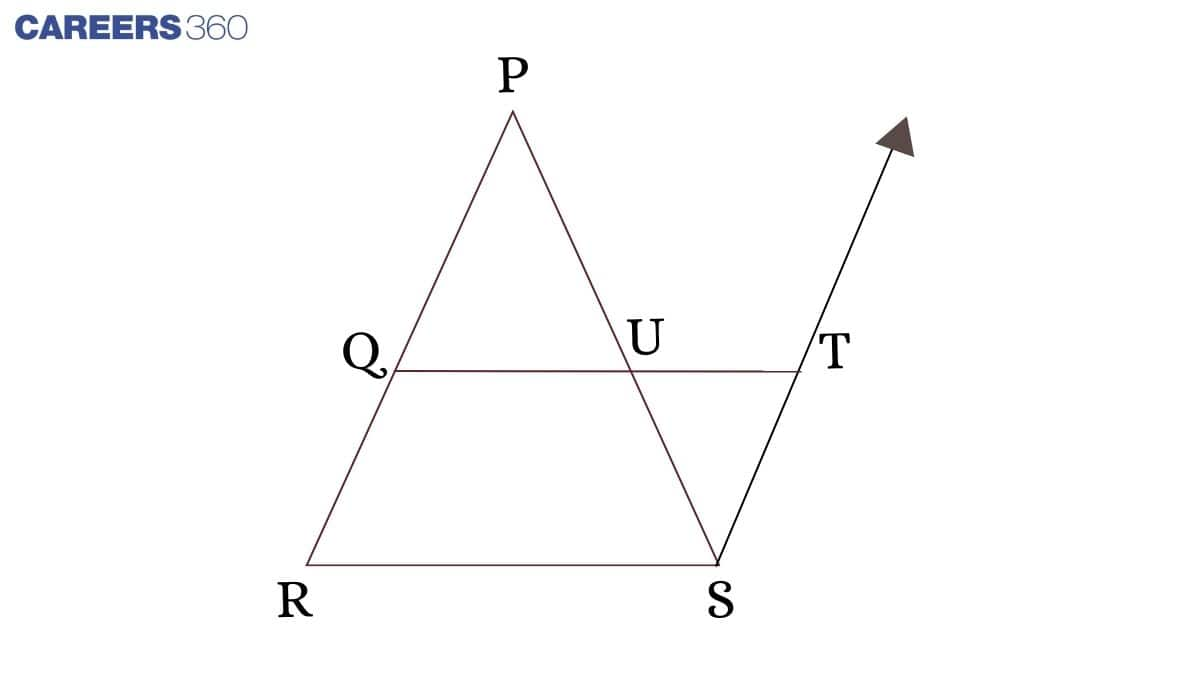
In ΔPRS, Q is the midpoint of U; U is the midpoint of PS.
Draw a line QU to T such that QU = UT
In ΔPQU and ΔUST,
∠PUQ = ∠TUS (Vertically opposite angles)
PU = US (U is the midpoint of PS)
QU = UT (From construction)
∴ΔPQU ≅ΔUST (By SAS rule)
Therefore,
∠QPU =∠TSU….(1)
PQ = TS = QR (Q is the midpoint of PR)
TS || PQ || PR (From equation (1))
TS || RQ
Therefore, QRST is a parallelogram.
Therefore, RS = QT and RS || QT
Therefore QU || RS

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Syllabus for Class 9

• NCERT Books for Class 9