Constructions Class 9th Notes - Free NCERT Class 9 Maths Chapter 11 Notes - Download PDF

NCERT Class 9 Maths Chapter 11 Notes

Introduction: The class 9 Maths Chapter 11 notes give the idea of chapter 11 in the NCERT book. Construction class 9 notes is the summary of the chapter and cbse class 9 maths chapter 11 notes discusses the construction of diagrams, an important aspect of geometry. The primary topics covered in class 9th maths chapter 11 notes are Basic construction like constructing a bisector, constructing the perpendicular bisector of a given line segment, Constructions of triangles. These are the important topics in ncert class 9 maths chapter 11 notes. Examples are not covered in notes for class 9 maths chapter 11. These given notes - ncert notes for class 9 maths chapter 11 are very helpful for revision. Construction notes are important for the CBSE exam and can be downloaded from class 9 maths chapter 11 notes pdf download or Construction class 9 notes pdf download.

Also, students can refer,

• NCERT Class 9 Maths Notes
• NCERT Solutions for Class 9 Maths Chapter 11 Constructions
• NCERT Exemplar Class 9 Maths Chapter 11 Solutions Constructions

NCERT Class 9 Maths Chapter 11 Notes

Basic Construction

To Construct The Bisector of A Given Angle

Give an angle ABC, to construct its bisector.

Steps of Construction:

• Draw an arc intersecting BA and BC at E and D with B as the center and any radius, as shown in figure
• Next, draw arcs that intersect at F, using D and E as centers and a radius of more than 1/ 2 DE.
• Draw the BF ray, see in Fig. A bisector of the angle ABC is ray BF. Now let me demonstrate the method.

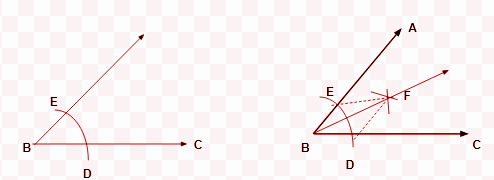
Join DF and EF.

In triangles BEF and BDF,

BE = BD (Radii of the same arc)

EF = DF (Arcs of equal radii)

BF = BF (Common)

Therefore, ∆BEF ≅ ∆BDF (SSS rule)

This gives ∠EBF = ∠ DBF (CPCT)

To Construct The Perpendicular Bisector of A Given Line Segment.

Given a line segment AC, we have to construct its perpendicular bisector.

Steps of construction

• Draw arcs on both sides of the line segment AC, using A and C as centers and a radius greater than 1/2 AC (to intersect each other).

• Let these arcs intersect each other at B and D. Join BD as shown in Fig.

• At point P, BD intersects AC. The perpendicular bisector of AC then lines BPD. Now let us demonstrate this method how this method gives us the perpendicular bisector of AC.

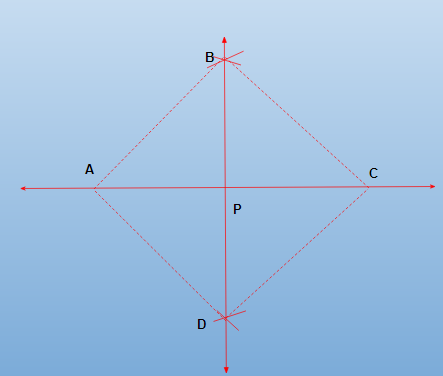
Join A and C to both B and D to form AB, AD, CB, and CD.

In triangles ABD and BCD,

AB = CB (Arcs of equal radii)

AD = CD (Arcs of equal radii)

BD = BD (Common)

Therefore,

∆ BAD ≅ ∆ BCD (SSS rule)

So, ∠ ABP = ∠ CBP (CPCT)

Now in triangles BPA and BPC,

AB = CB (As before)

BP = BP (Common)

∠ ABP = ∠ CBP (Proved above)

Therefore,

∆ BPA ≅ ∆ BPC (SAS rule)

So,

AP = CP

and ∠ BPA = ∠ BPC (CPCT)

As ∠ BPA + ∠ BPC = 180° (Linear pair axiom),

we get ∠ BPA = ∠ BPC = 90°.

Therefore, BP, that is, BPD is the perpendicular bisector of AC.

To Construct An Angle of 60° At The Initial Point of A Given Ray

Let us take a ray ST with initial point S as shown in Fig. We want to construct a ray SR such that

∠ RST = 60°.

Steps of Construction:

• Draw an arc of a circle that intersects ST, say at point D, using A as the center and some radius.

• Draw an arc of the same radius as before intersecting the previously drawn arc, say at point C, with D as its center.

• Draw the SR ray as it passes through C as shown in Fig.

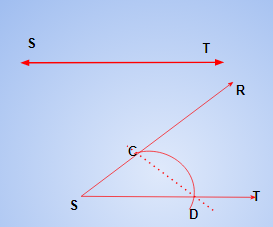
Then ∠ RST is the required angle of 60°. Now, let us demonstrate this method how this method gives us the required angle of 60°.

Join CD.

Then, SD = SC = CD (By construction)

Therefore,

∆ CSD is an equilateral triangle, and the ∠ CSD, which is the same as ∠ RST is equal to 60°.

Rules of Congruency of Two Triangles

• Side-Angle-Side (SAS): Two triangles are congruent when any two sides and the included angle of one triangle are equal to any two sides and the included angle of the other triangle.

• Side-Side-Side (SSS): Two triangles are congruent when the three sides of a triangle are equivalent to the 3 sides of the other triangle.

• Angle-Side-Side (ASA): The triangles are congruent when any two angles and the included side of one triangle are equivalent to the two angles and the included side of the other triangle.

• Right Angle-Hypotenuse-Side (RHS): The triangles are congruent when the hypotenuse and a side of one triangle are equal to the hypotenuse and a side of the other triangle.

A triangle is unique if:

• Two sides are given, as well as the included angle.

• If there are three sides available.

• Two angles are framed, as well as the included side, and

• The hypotenuse and one side of a right triangle are provided.

Now Discuss Some Constructions of Triangles

Given A Base, A Base Angle, And The Sum of The Other Two Sides

Construct a triangle ABC using the given data.

Base BC, a base angle ∠B, and the sum AB + AC of the other two sides of a triangle ABC.

Construction Procedures:

1. Draw the base AB, and at point A, make an angle, say XAB, equal to the given angle.

2. Cut a line segment AD equal to CA + CB from the ray AX.

3. Make a DBY angle equal to ADB by joining DB.

4. At C, BY intersects AX as shown in Fig.

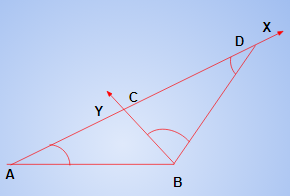
The required triangle is CAB. Let us see how we get the required triangle.

Base AB and ∠A are drawn as given.

In triangle CBD,

∠CBD = ∠CDB (By construction)

Therefore,

CB = CD and then

CA = AD – CD = AD – CB

CA + CB = AD.

Given Its Base, A Base Angle, And The Difference Between The Other Two Sides

Let the base PQ, a base angle, say ∠P, and the difference of the other two sides RP – RQ or RQ - RP you have to construct the triangle RPQ.

Clearly, there are the following two cases:

Case (i): Let RP > RQ that is RP – RQ is given.

Steps of Construction:

1. Draw the base PQ and at point P make an angle say XPQ equal to the given angle.

2. Cut the line segment QS equal to RP – RQ from ray PX.

3. Join QS and draw the perpendicular bisector, say LM of QS.

4. Let it intersect PX at point R. Join RQ as shown in fig.

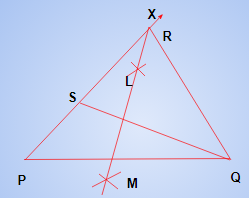
Then RPQ is the required triangle. Let us see how we have obtained the required triangle RPQ.

Base PQ and ∠P are drawn as given.

Point Q lies on the perpendicular bisector of SQ.

Therefore,

RS = RQ

So,

PS = RP – RS = RP – RQ.

Case (ii) : Let RP < RQ that is RQ – RP is given.

Steps of Construction:

1. Same as in case (i).

2. Cut the line segment PS equal to RQ – RP from the line PX extended on the opposite side of line segment PQ.

3. Join QS and draw the perpendicular bisector, say LM of SQ.

4. Let LM intersect PX at R. Join RQ as shown in fig.

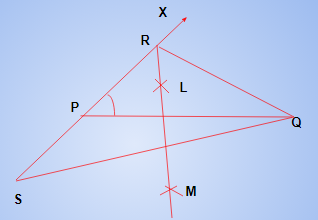
Then, RPQ is the required triangle. The construction can be explained as in case (i).

Given Its Perimeter And Its Two Base Angles

Given the base angles, say ∠ C and ∠ D and CD + DR + RC, you have to construct the triangle RCD.

Steps of Construction:

1. Draw a line segment, say PQ equal to CD + DR + RC.

2. Make angles APQ equal to ∠P and AQP equal to ∠Q.

3. Bisect ∠ APQ and ∠ BQP. Let these bisectors intersect at a point R [see Fig (i)]

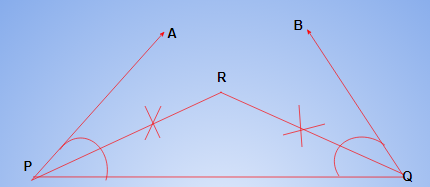
4. Draw perpendicular bisectors LL’ of RP and MM’ of RQ.

5. Let LL’ intersect PQ at C and MM’ intersect PQ at D. Join RC and RD [see Fig (ii)].

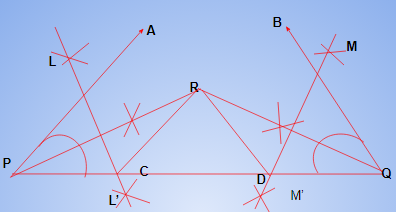
Then RCD is the required triangle.

Using the construction as a basis, you note that C lies on the perpendicular bisector LL’ of RP.

Therefore,

PC = RC and similarly, DQ = RD.

This gives

CD + DR + RC = CD + PC + DQ = PQ.

Again ∠CRP = ∠RPC (As in ∆ RPC, RC = PC)

and

∠RCD = ∠CRP + ∠RPC = 2 ∠RPC = ∠APQ

Similarly,

∠RDC = ∠DQD as required.

Significance of NCERT class 9 maths chapter 11 notes

Construction class 9th notes will help students to understand the formulas, statements, and rules in detail. The ncert class 9 maths chapter 11 notes contain previous year’s questions and NCERT textbook pdf. These topics can also be downloaded from Class 9 maths chapter 11 notes pdf download or Construction class 9 notes pdf download.

NCERT solutions of class 9 subject wise

• NCERT solutions for class 9 Maths
• NCERT solutions for class 9 Science

NCERT Class 9 Exemplar Solutions for Other Subjects:

• NCERT Exemplar Class 9 Maths solutions
• NCERT Exemplar Class 9 Science solutions

NCERT Class 9 Notes Chapter wise