Motion Class 9th Notes - Free NCERT Class 9 Science Chapter 8 Notes - Download PDF

NCERT Class 9 Science Chapter 7 Notes

Class 9 Science Chapter 7 Motion Notes gives a clear and concise overview of all the crucial concepts to enable the students to revise effectively and in a short time. These Motion Class 9 Science Chapter 7 CBSE notes are made in accordance with the recent CBSE syllabus so that definitions, formulae, diagrams and so on are easily understandable. They are a very good study aid in the preparation of exams, reinforcement of basic concepts and a solid study base in advanced classes.

Motion Along a Straight Line

• A straight-line motion is the most basic sort of motion. Distance and Displacement are two separate quantities used to represent an object's overall motion and to locate its end position in relation to its initial position at a given moment.
• In physics, distance refers to the length of an object's path (the line or curve) through space.
• Distance is not dependent on direction. Scalars are physical quantities that can be described completely without the need for direction.
• The shortest distance between a body's initial and final positions, as well as its direction, is called displacement as it moves from one location to another.
• Because displacement requires both direction and magnitude to be fully described, such physical quantities are referred to as vectors.
• A moving body's distance travelled cannot be zero, yet its eventual displacement can be zero.

Uniform Motion and Non-Uniform Motion

• A body is said to be in uniform motion if it travels equal distances at equal intervals of time. Non-uniform motion occurs when a body traverses unequal distances in equal intervals or equal distances in unequal intervals.

Speed

• The total distance travelled by the object during the time interval in which the motion occurs is defined as its speed. The metric unit of speed is the meter per second. So, Speed=Distance travelled/time taken=s/t

Here 's' is the distance travelled by the object and t is the time taken by the object to travel the distance s. The speed of a body tells us how slowly or quickly it is moving. The average speed of a body is determined by the ratio of the total distance travelled to the total time spent by the body. A body's instantaneous speed is its speed at a given instant. If a body travels the same distance in equal intervals of time, it is said to have constant or uniform speed.

Velocity

• The rate at which a body's displacement changes with time is referred to as its velocity.
• In SI units, an object's velocity is measured in meters per second.
• Velocity is simply the speed of an object moving in a specific direction. An object's velocity can be either uniform or variable. It can be altered by varying the speed, direction, or both of the object's motion. So velocity is a vector quantity, whereas speed is a scalar quantity with only magnitude and no specific direction.
• When a body travels the same distance in the same period of time in the same direction, it is said to be moving at uniform velocity. If a body covers unequal distances in equal intervals of time and vice versa in a specified direction, or if it changes direction, it is said to be moving with non-uniform velocity.
• A body's velocity can be changed in two ways: first, by changing its speed, and second, by changing its direction of motion while keeping its speed constant. In order to change the velocity of the body, both the speed and direction of the body can be changed.
• When the velocity of an object changes at a constant rate, the arithmetic mean of the initial and final velocity for a given period of time is used to calculate average velocity, which is average velocity =(u+v)/2

where u is the initial velocity of the body and v is the final velocity of the body.

Acceleration

• The change in velocity of an object per unit time is called acceleration. It is given as,

Acceleration=Change in velocity/time taken

• If the velocity of a body varies from an initial value u to a final value v in time t. Acceleration ‘a' is given by,

a = (v-u)/t

• If a body moves in a straight path and its velocity increases by the same amount every time interval, it is said to have uniform acceleration. Examples include freely falling bodies, balls rolling down an inclined plane, and so on.
• If a body's velocity changes by an unequal amount at equal periods of time, it is said to have non-uniform acceleration.
• Positive acceleration occurs when acceleration occurs in the direction of velocity; negative acceleration occurs when acceleration occurs in the opposite direction of velocity; negative acceleration is known as retardation.

Equations of Motion

1. First Equation of Motion

• v=u+at is the first equation of motion, where v is the final velocity and u is the body's initial velocity. The first equation of motion determines the body's velocity at any time t.

We know, Acceleration = Change in velocity time taken

So, a = (v-u)/t

∴ at=v-u

Now, rearranging the above equation, we get,

v=u+at

In this manner, we get the first equation of motion.

2. Second Equation of motion:

• s=ut+at²/2 is the second equation of motion. ‘u’ is the initial velocity here, ‘s’ is the distance travelled by the body in time ‘t’ and ‘a’ is the uniform acceleration.

Now consider the average velocity formula, when the velocity of an object changes at a constant rate. That is,

average velocity=(u+v)/2

Distance travelled by an object is,

s= (u+v)t/2

The first equation of motion is, v=u+at

Substituting the first equation of motion in the above equation, we get

s=(u+u+at)t/2

=(2u+at)t/2

=(2ut+at²)/2

Rearranging the above equation, we get,

s=ut+at²/2

3. Third Equation of motion:

• v²=u²+2as is the third equation of motion. ‘u’ is the initial velocity here, ‘v’ is the final velocity. ‘s’ is the distance travelled by the body in time ‘t’ and ‘a’ is the uniform acceleration.

This equation gives the body's velocity as it travels a distance of s.

v=u+at and s=ut+at²/2 are the first and second equations of motion, respectively.

Rearranging the first equation, we get,

t=(v-u)/a

Substituting this in the second equation of motion, we get,

s=u((v-u)/a + a((v-u)/a)²/2

s=(2uv-2u²+v²+u²-2uv)/2a

Rearranging the above equation, we get,

v²=u²+2as

• The following three crucial points should be remembered while addressing uniformly accelerated motion problems using these three equations of motion.

1. u=0 is the initial velocity of a body starting from rest.
2. When a body comes to a complete stop, its final velocity is equal to zero.
3. The acceleration of a body moving at a constant velocity is zero.

Graphical representation of motion

• A graph depicts the relationship between two sets of data, one of which contains dependent variables and the other of which contains independent variables.
• Line graphs can be used to depict the motion of an object. Line graphs in this case show the relationship between one physical quantity, such as distance or velocity, and another physical quantity, such as time.

1. Distance Time Graphs

• On a distance-time graph, the change in an object's position over time can be represented.
• The x-axis in this graph represents time, while the y-axis represents distance.
• Because they precisely depict velocity, distance-time graphs of a moving body can be utilised to compute the speed of the body.
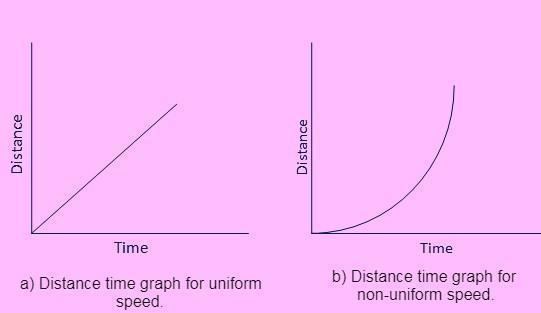
• As illustrated in Figure a, the distance-time graph for a body moving at a constant speed is always a straight line since the distance travelled by the body is directly proportional to time.
• The distance-time graph for a body travelling at a non-uniform speed is depicted in figure 'b' below as a curve.

• When the object is at rest, the distance-time graph is parallel to the time axis, as shown in the figure (a) below,

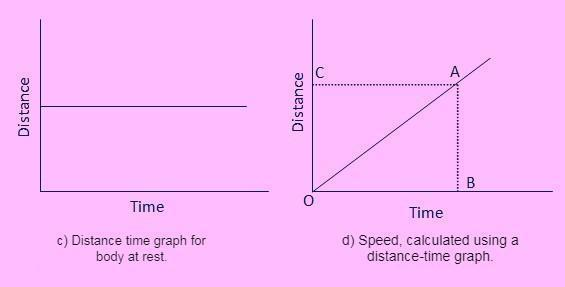
To determine the body's speed from a distance time graph [figure d)], say at point A, first draw a perpendicular AB on the time axis and a perpendicular AC on the distance axis, so that AB represents the body's distance travelled in the time interval OB, and we know,

Speed=Distance travelled/time taken=s/t=AB/OB

2. Velocity time graphs

• A velocity-time graph depicts the variation in velocity with time for an object travelling in a straight line. Time is shown on the x-axis, while velocity is displayed on the y-axis in this graph. The displacement of an object travelling with uniform velocity is given by the product of velocity and time. The magnitude of the displacement will be equal to the area contained by the velocity-time graph and the time axis.
• If a body moves at a steady velocity, its velocity-time graph will be a straight line parallel to the time axis, as seen in Figure (e).

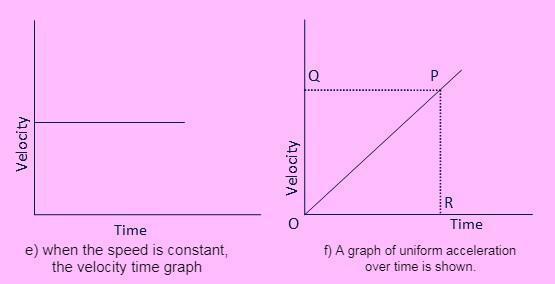
Figure f) depicts a straight-line velocity time graph with uniformly changing velocity. The velocity-time graph can be used to determine the value of acceleration.

Draw a perpendicular RP from point R to calculate acceleration at the time corresponding to point R, as shown in figure f).

Acceleration=Change in velocity/time taken

The time taken is equal to OR, and the change in velocity is indicated by PR.

Acceleration=PR/OR

This is the same as the velocity-time graph's slope. As a result, we can deduce that the slope of a moving body's velocity-time graph determines its acceleration.

As shown in Figure f), the distance travelled by a moving body in a given time is equal to the area of the triangle OPR.

Distance travelled=Area of triangle OPR

=0.5Area of rectangle ORPQ

Thus, Distance travelled=(OQ)(OR)/2

When a body's velocity varies in an irregular pattern, the body's velocity-time graph is a curved line.

Equations of motion by the graphical method

When an object moves in a straight path with uniform acceleration, we already understand equations of motion. We already know how to calculate them, but a graphical way can also be used.

1. Equation for velocity time relation:

Consider the velocity-time graph of an object moving with uniform acceleration, as seen in Figure a).

The initial velocity of the object is u (at point A) and rises to v (at point B) in time t, as shown by this graph. The velocity is changing at a constant rate of a.

Again, the time‘t’ is represented by OC, the initial velocity u by OA, and the final velocity of the body after time t by BC in the figure.

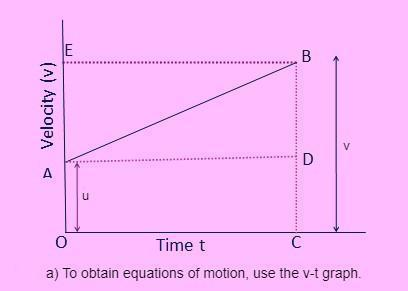
The graph in figure (a) clearly shows that BC=BD+DC=BD+OA. As a result,

We have v = BD+u ……………………………… (1)

We should now determine the value of BD. The object's acceleration from the velocity-time graph is given by,

Acceleration=Change in velocity/time taken=BD/AD=BD/OC=BD/t

We get, BD=at

Substituting the value of BD in eqn (1) we get,

v=u+at

which is the first equation of motion and velocity-time relation

2. Equation for position time relation:

Assume the body has travelled 's' distance in time t with uniform acceleration a. The area encompassed within OABC under the velocity-time graph AB in Fig. (a) is used to calculate the distance travelled by the body.

Thus, the object travels a distance, which is given by,

s = Area of OABC (trapezium).

s = area of the rectangle OADC + area of the triangle ABD.

s=OA x OC+(AD)(BD/2

Putting OA= u, OC = t and BD = at, we have

s=(u x t)+(t x at)/2

Then we get,

s=ut+at²/2

This is an equation of the position-time relation.

3. Equation for position velocity relation:

Consider the graph in Figure (a). We know that the area under the line AB, which is the area of the trapezium OABC, gives the distance s travelled by a body in time t.

Thus, we have.

distance travelled by object= s=Area of trapezium OABC

s=(sum of parallel sides x height)/2=(OA+CB) x OC/2

we have, OA+CB=u+ v and OC=t, so we have

s=(u+v)t/2

By velocity time relation, t=(v-u)/a

Substituting this ‘t’ in the equation for ‘s’, we have,

s=(u+v)(v-u)t/2a

Therefor,e we have,

v²=u²+2as

This is an equation for the position-velocity relation.

Uniform circular motion

• The motion of an object is called uniform circular motion when it moves along a circular route at a constant speed.
• Many examples of circular motion may be found in our daily lives, such as vehicles driving around a circular track and many others.
• In addition, the Earth and other planets orbit the Sun in roughly circular orbits.
• Even if the speed of a particle moving in a circular motion remains constant, the particle accelerates due to the continually changing direction of the velocity. A uniform circular motion occurs when an object moves in a circular orbit at a constant speed.
• In circular motion, we use angular velocity instead of velocity as we did in linear motion. The force required to move a body along a circular route is referred to as centripetal force.
• We know that 2πr equals the circumference of a circle of radius r. If a body takes t seconds to move once around a circular path of radius r, the velocity v is given by v =2πrt.
• Although uniform linear motion is not accelerated, uniform circular motion is.

NCERT Class 9 Science Chapter 7 Motion: Previous Year Question and Answer

Previous Year Question and Answer Class 9 Science Chapter 7 Motion gives students a clear picture of the kind of questions that are normally askedṁ. These PYQs assist in reinforcing the conceptual knowledge of motion, graphs and formulae by using them on real exam-type questions. These questions enhance accuracy, confidence and equip the students well in case they are to be tested in school and in their end-of-year exams.

Q1: A particle is moving with constant acceleration from A to B in a straight line AB. If u and v are the velocities at A and B, respectively, then its velocity at the midpoint C will be:

Answer:

If the length of $A B=s$, then mispoint of $A B$ is at $s / 2$
The velocity of the particle changes from $u$ to $v$ when it moves through the distance $s$

$
a=\frac{v^2-u^2}{2 s}
$

Velocity at midpoint is

$
v_c^2=u^2+\frac{2 a s}{2} \ldots
$

Substituting (1) in (2), we get

$
\begin{aligned}
& v_c^2=\frac{v^2+u^2}{2} \\
& v_c=\sqrt{\frac{v^2+u^2}{2}}
\end{aligned}
$$\begin{array}{r}\end{array}$

Q2: The velocity-time plot for a particle moving on a straight line is shown in the figure.

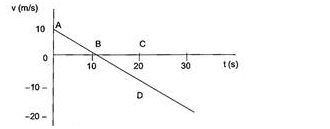
(a) The particle has a constant acceleration

(b) The particle has never turned around.

(c) The particle has zero displacement.

(d) The average speed in the interval 0 to 10s is the same as the average speed in the interval 10s to 20s.

Which of the above statements are correct?

Answer:

Since the velocity-time graph is a straight line, the slope of this straight line is constant, and hence the particle has a constant acceleration, and the areas OAB and BCD are the same, so the average speeds in the intervals 0 to 10 s and 10 s to 20 s are the same.

Hence, the correct options are (a) and (d)

Q3: The graph below shows the distance travelled and the time taken by four cars.

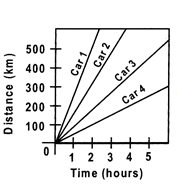
Which car travelled the slowest?

Answer:

The slope of the distance-time graph represents the velocity. The slope for car 4 is the minimum, so its speed is also the minimum.

Hence, car 4 travels the slowest.

How to Master Class 9 Science Chapter 7 Motion?

To be able to master Class 9 Chapter 7 of science- Motion, you have to have a solid understanding of the fundamental concepts, such as distance, displacement, speed, velocity, and acceleration. This chapter is the basis of kinematics, which is very important in the higher classes and competitive exams. Having clear ideas, frequent practice of the numerical problems, and proper revision of graphs and formulas, students can easily obtain all the marks. The systematic method of study assists in the creation of conceptual long-term clarity in physics.

• Begin with an overview of the fundamental concepts of distance, displacement, speed, velocity, and acceleration, which are the basics of the chapter.
• Learn the differences between uniform and non-uniform motion using practical examples in life.
• Learn about motion graphs(distance-time graph and velocity-time graph) because they are mostly asked in the exams.
• Learn the three equations of motion and know what they mean instead of memorising.
• Solve equations of motion by solving numerical problems to enhance speed and accuracy.
• Revise graphical derivations of equations of motion because they enhance conceptual knowledge.
• Go through the NCERT solved examples before attempting the exercise questions.
• Create a summary sheet of all formulas, definitions, and SI units where formulae and definitions come in handy.
• Use diagrams and graphs to visualise the movement of an object under various conditions.
• Solve last year's questions, sample papers, and school test papers to get the picture of the exam pattern.

Importance of Class 9 Physics Chapter 7 Motion Notes

Motion Class 9 Science Chapter 7 CBSE notes are very crucial since they explain complex topics such as speed, velocity, acceleration, and graphical representation of motion, which would otherwise be very difficult to learn and remember among students. These notes will include brief explanations, major formulas, solved numerical problems, and clear diagrams that assist in enhancing the conceptual clarity. They are also a good source of revision during CBSE exams and allow one to remember definitions, equations of motion and key graphs with ease. Furthermore, Motion Class 9 Science Notes enable students to have a solid background of higher-level physics subjects in later classes, particularly kinematics in Class 11. The highly organised material facilitates exam preparation and increases competence in problem-solving. These notes are also very useful when using them during competitive exams such as NTSE, Olympiads, JEE, and NEET, when motion and kinematics make up much of the physics curriculum. These Motion Class 9 Science Notes are useful and make learning and performance in school and competitive exams easy by simplifying explanations and providing material to write in the exams.

NCERT Solutions of Class 9 Subject-Wise

• NCERT solutions for class 9 Maths
• NCERT solutions for class 9 Science

NCERT Class 9 Exemplar Solutions for Other Subjects:

• NCERT Exemplar Class 9 Maths solutions
• NCERT Exemplar Class 9 Science solutions

NCERT Class 9 Science Chapter Wise Notes

The NCERT Class 9 science chapter-wise notes help the student in having an organised and convenient way of accessing the entire chapter in a single place. These notes make significant ideas, equations, and schemes simple based on the current CBSE syllabus. Chapter-based links enable students to update faster, keep track of things, and prepare better to take exams.