NCERT Class 9 Maths Chapter 6 Notes Lines and Angles

Updated on 23 Apr 2025, 11:40 AM IST

The chapter Lines and Angles provides the first introduction to geometrical fundamentals. The chapter investigates basic geometric elements that start with points and lines, and rays and continues to explain angle varieties produced by transversal intersections or cuts of lines. Basic geometric understanding depends on these core concepts for learning advanced mathematical shapes that appear later in the textbook.

This Story also Contains

NCERT Notes Class 9 Maths Chapter 6 Lines and Angles
Basic Terms and Definitions
Class 9 Chapter Wise Notes
NCERT Solutions for Class 9
NCERT Exemplar Solutions for Class 9
NCERT Books and Syllabus

Lines and Angles

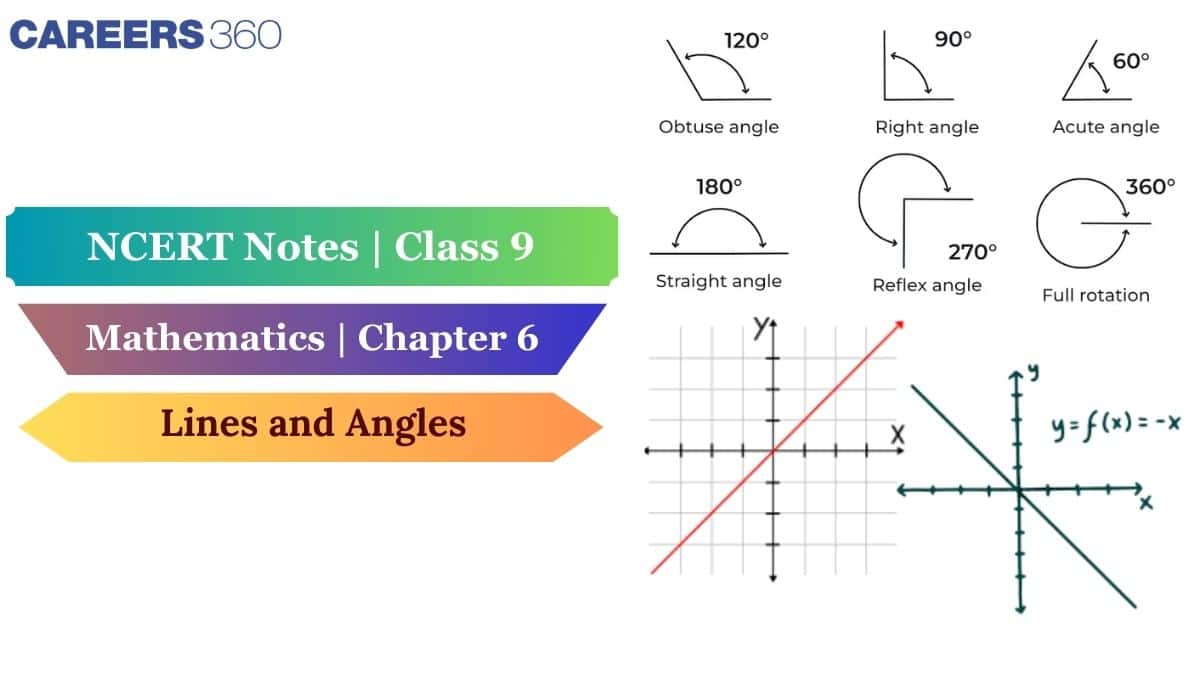
The chapter covers four angle types - acute, right, obtuse, and straight - combined with complementary, supplementary, adjacent and vertically opposite angle pairs. The study of lines intersecting with transversals results in the evaluation of corresponding angles and alternate interior angles, along with other angle properties. All advanced geometry studies require a fundamental understanding of these concepts. Students should utilise the NCERT class 9th maths notes to learn and review various concepts, while using the NCERT notes for supplementary notes on higher-level chapters if needed.

NCERT Notes Class 9 Maths Chapter 6 Lines and Angles

Basic Terms and Definitions

Line Segment:

A portion of the line with two endpoints is called a line segment. It is denoted by the symbol $\overline{AB}$.

1744530889243

Ray:

A part of the line with one endpoint and the other endpoint extending up to infinity. It is denoted by the symbol $\overrightarrow{AB}$.

1744530978589

Collinear Points:

If three or more points lie on the same line, they are called collinear points.

Non-Collinear Points:

If three or more points do not lie on the same line, they are called non-collinear points.

Angle:

An angle is generated when two rays originate from the same point. The rays making an angle are called the arms of the angle, while the vertex refers to the place where they end.

Types of Angles:

In geometry, there are several types of angles. The fundamental component of geometry in Mathematics is the angles.

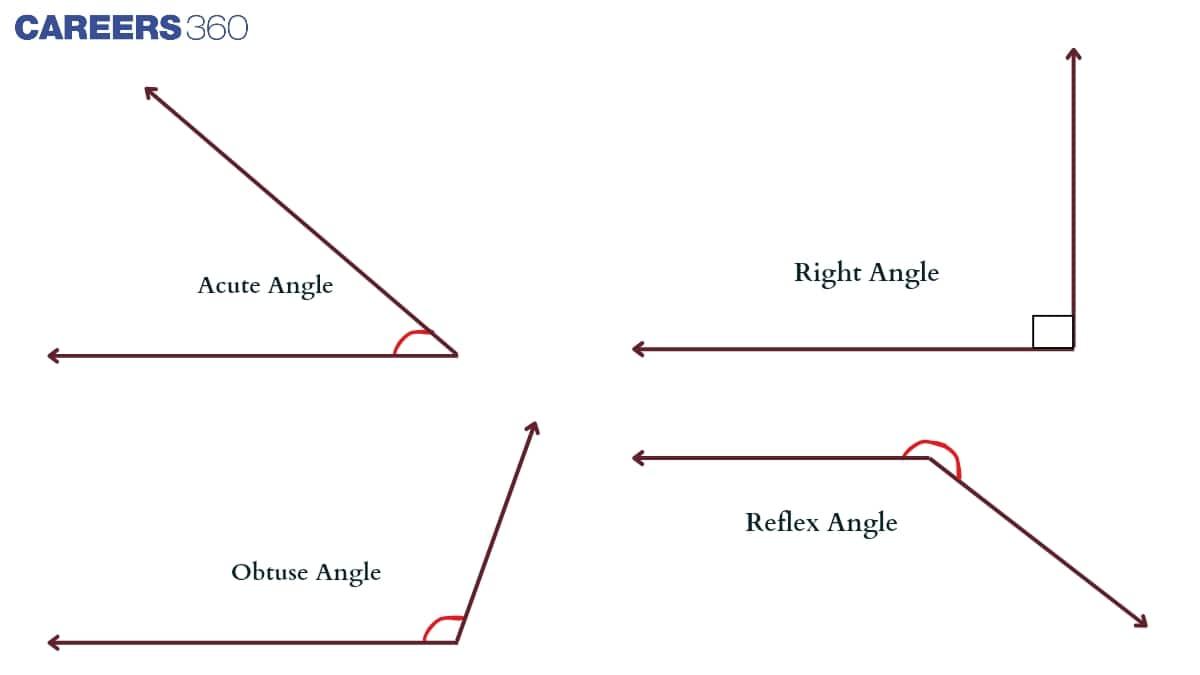
Acute Angle: Measures greater than 0° and less than 90°. It means acute angles are when: 0° < angle < 90°.
Right Angle: Measures equal to 90°. It means right angles are when: Angle = 90°.
Obtuse Angle: Measures greater than 90° and less than 180°. It means obtuse angles are when: 90° < angle < 180°.
Straight Angle: Measures equal to 180°. It means straight angles are when: Angle = 180°.
Reflex Angle: Measures greater than 180° and less than 360°. It means reflex angles are when: 180° < angle < 360°.

1744531009539

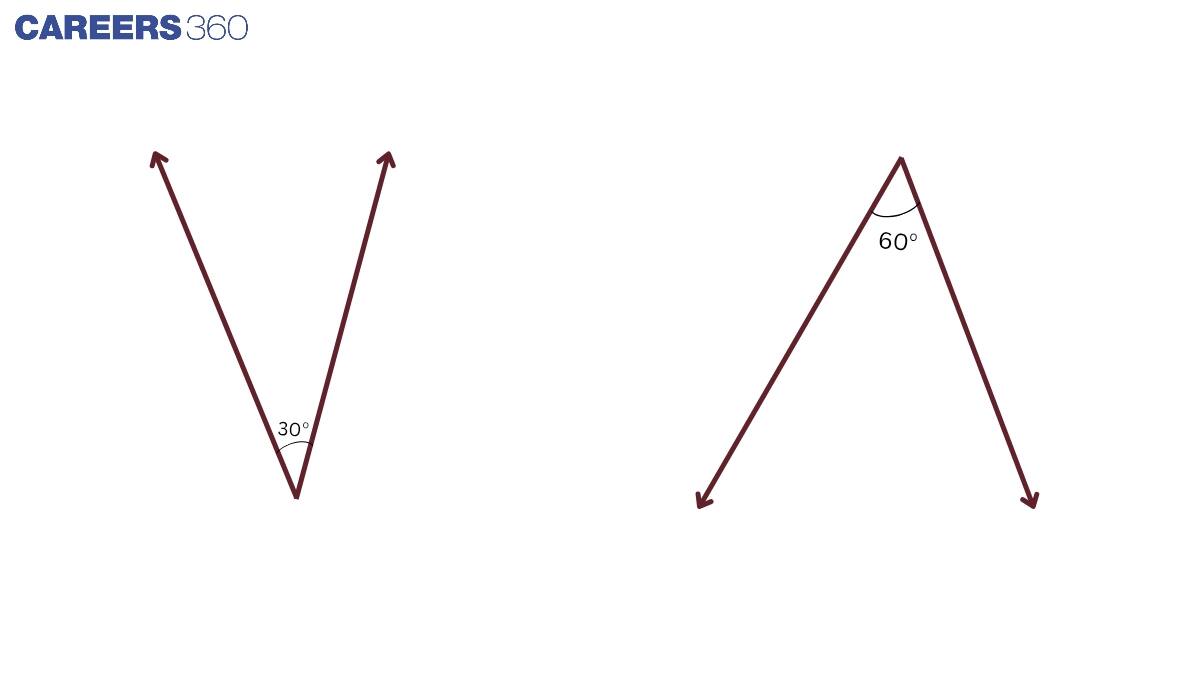
Complementary Angles:

When the sum of two angles is 90°, they form up complementary angle.

1744531028715

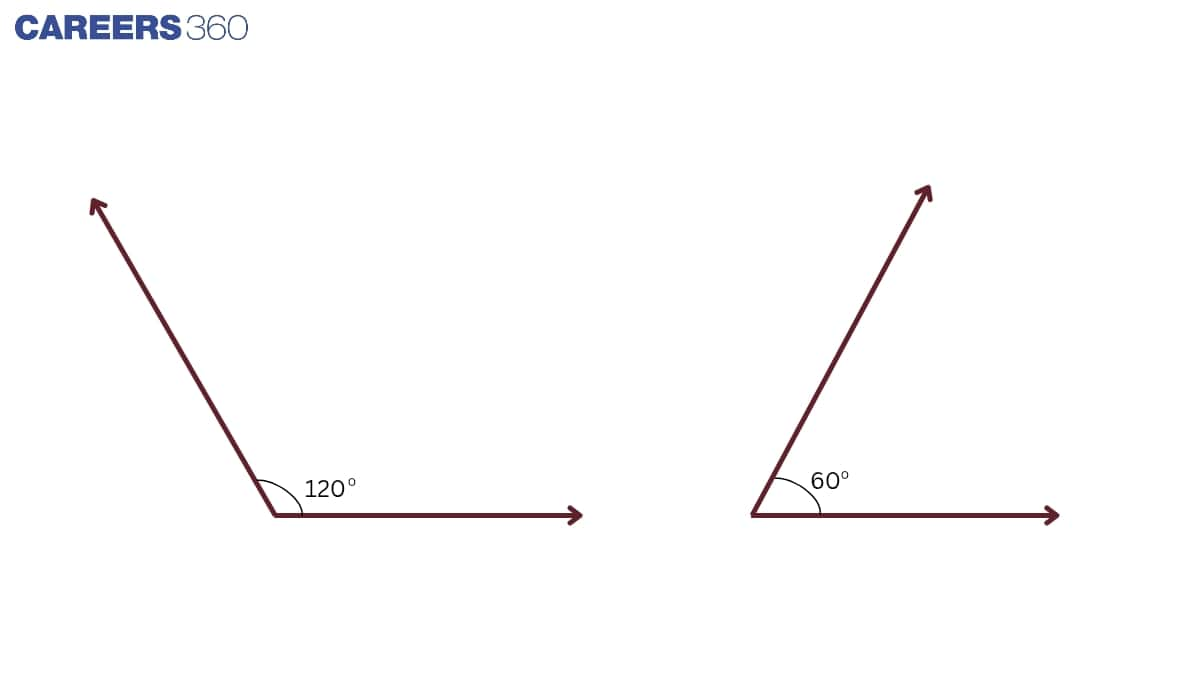
Supplementary Angles:

When the sum of two angles is 180°, they form up supplementary angle.

1744531048413

Adjacent Angles:

If angles have a common vertex, a common arm, and their non-common arms are on different sides of the common arm, they are called adjacent angles.

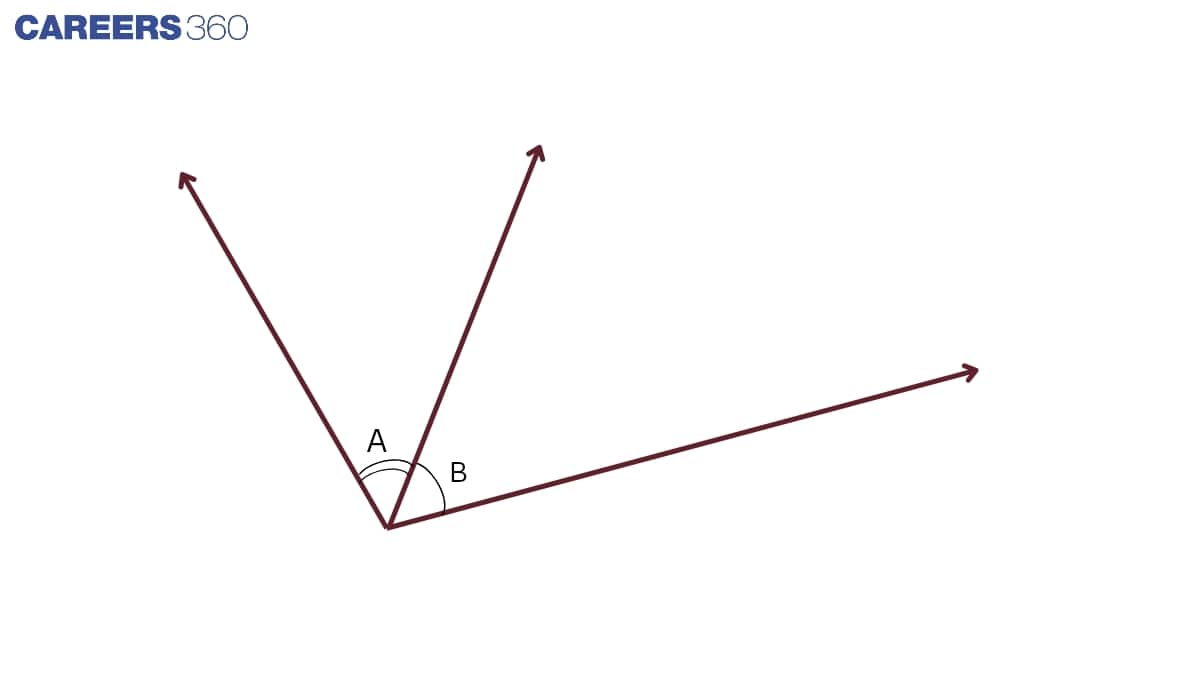
1744531076213

Linear pair of angles:

A pair of adjacent angles whose non-common sides create a straight line that adds up to 180°.

1744531098124

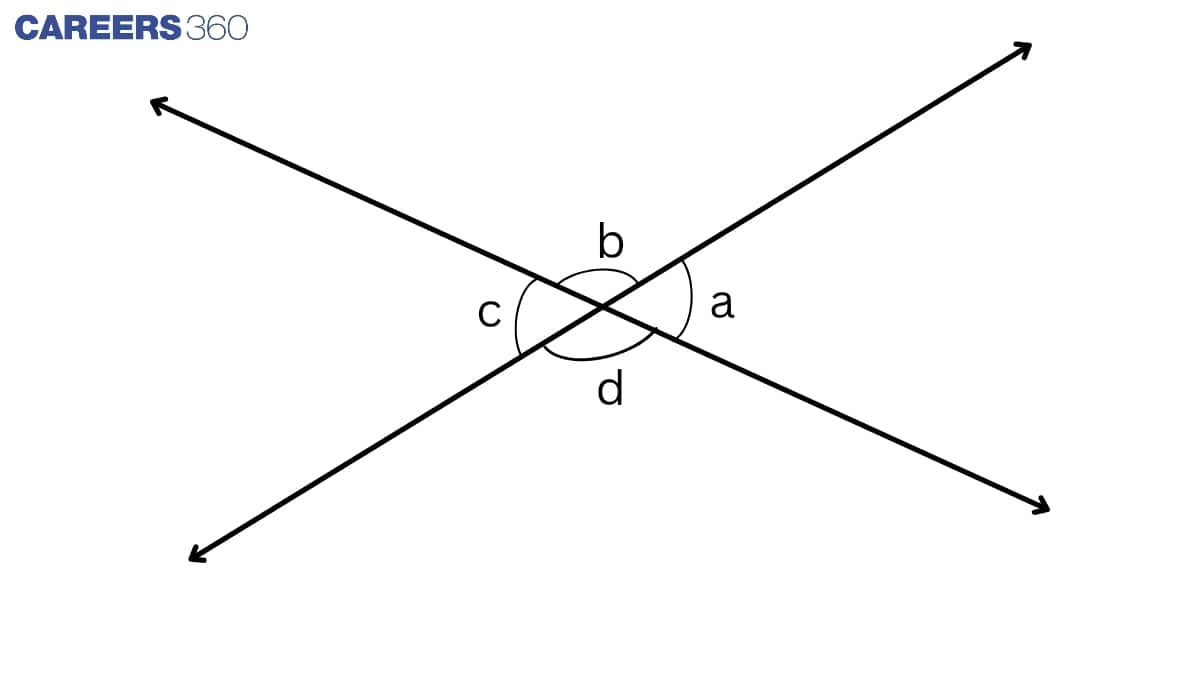
Vertical Opposite angles:

If two lines intersect each other at a point, they form vertically opposite angles which are equal to each other. Like in the given figure, angles a and c, b and d are vertically opposite angles.

1744531119110

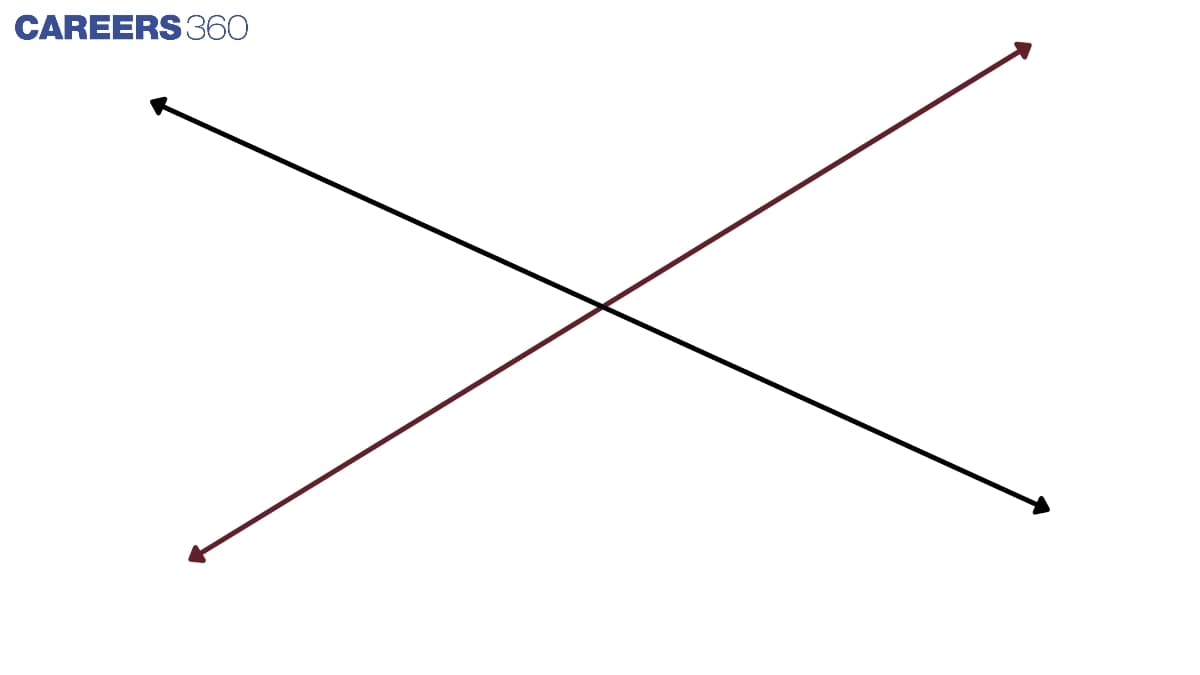
Intersecting Lines:

When the lines cross each other at a single point, they are called Intersecting lines.

1744531149501

Non-Intersecting Lines:

When the lines are parallel to each other, or do not intersect, they are called non-intersecting lines.

1744531179969

Pair of Angles Axioms:

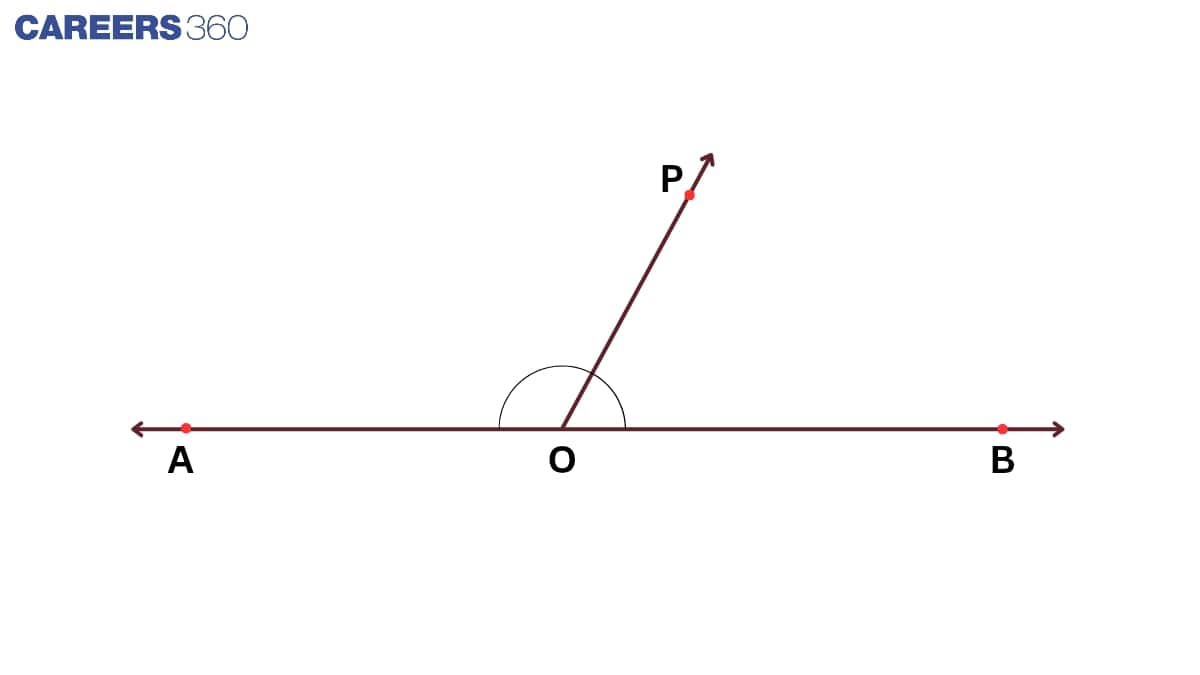
Axiom - Linear Pair of Angles:

If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.

Axiom - Converse of Linear Pair of Angles:

If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

Vertically Opposite Angles Theorem:

If two lines intersect each other, then the vertically opposite angles are equal.

Parallel lines with a Transversal:

A transversal defines a line which crosses different lines at different points. Like in the figure, t is the transversal line.

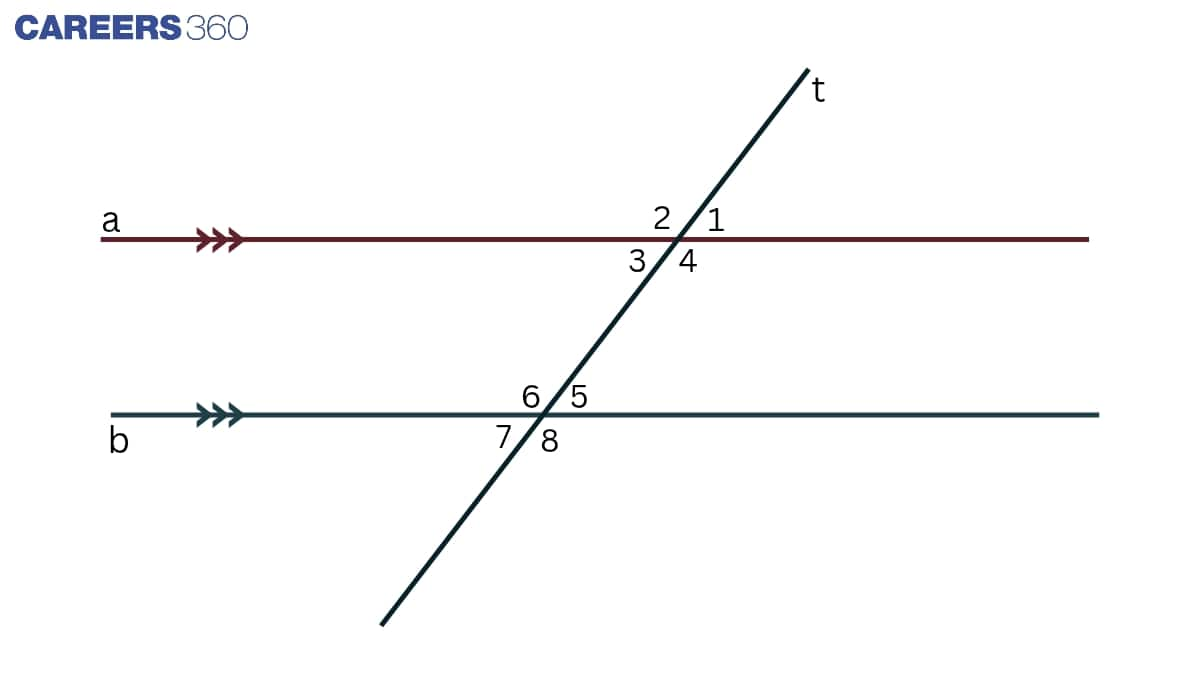
1744531213975

Corresponding angles axiom:

When a transversal intersects two parallel lines, then the Corresponding Angles are Equal.

Converse of the Corresponding Angles Axiom:

When a transversal line intersects two lines and the Corresponding Angles are equal, then the lines are parallel to each other.

Alternate Interior Angle Axiom:

When a transversal intersects two parallel lines, then the pair of alternate interior angles is equal.

Converse of Alternate Interior Angle Axiom:

When a transversal line intersects two lines and the alternate interior angles are equal, then the lines are parallel to each other.

The Sum of the Co-interior Angles is Supplementary Axiom:

When a transversal intersects two parallel lines, then the pair of interior angles on the same side of the transversal line are supplementary, i.e. equal to 180°.

The Converse of the sum of the Co-interior angles is supplementary Axiom:

When a transversal line intersects two lines and the interior angles on the same side of the transversal line are supplementary, then the lines are parallel to each other.

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Notes Class 9 Maths Chapter 1 - Number System

NCERT Notes Class 9 Maths Chapter 2 - Polynomials

NCERT Notes Class 9 Maths Chapter 3 - Coordinate Geometry

NCERT Notes Class 9 Maths Chapter 4 - Linear Equation in Two Variables

NCERT Notes Class 9 Maths Chapter 5 - Introduction To Euclid’s Geometry

NCERT Notes Class 9 Maths Chapter 6 - Lines and Angles

NCERT Notes Class 9 Maths Chapter 7 - Triangles

NCERT Notes Class 9 Maths Chapter 8 - Quadrilaterals

NCERT Notes Class 9 Maths Chapter 9 - Circles

NCERT Notes Class 9 Maths Chapter 10 - Heron's Formula

NCERT Notes Class 9 Maths Chapter 11 - Surface Areas and Volumes

NCERT Notes Class 9 Maths Chapter 12 - Statistics

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

Articles

Top 6 Career Options after BAF - Eligibility, Salary

Sep 06, 2025

Samagra Plus Question Bank & Model Question Papers (Class 1–12) – Download PDF

Sep 05, 2025

IOQM Admit Card 2025: Download Indian Olympiad Qualifier in Mathematics Hall Ticket

Sep 04, 2025

Haryana Open School Admission 2025: Apply Haryana Open Fresh 10th, 12th Online Form

Sep 04, 2025

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is