NCERT Solutions for Class 9 Science Chapter 7 Motion

Class 9 Science Chapter 7 Motion: Solved In-text Questions-

Topic 7.1 Describing Motions

Q 1. An object has moved through a distance. Can it have zero displacements? If yes, support your answer with an example.

Answer:

Yes, an object has moved through a distance can have zero displacements.

If an object moves and returns to the original position, the displacement will be zero. Consider the movement in a circular path. A man walks from point A in a circular path in a park and comes back to point A.

The distance traveled is equal to the circumference of the circular path, but displacement is zero.

Q 2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?

Answer:

Side of the square field = $10m$
$\therefore$ The perimeter of the square = $4\times 10=40m$
According to question,
He completes 1 round in $40s$ .
$\therefore$ Speed of the farmer = $\frac{40}{40}=1m/s$
$\therefore$ Distance covered in $2min20s(=140s)$ = $140\times 1=140m$
Now,
Number of round trips completed traveling = $\frac{140}{40}=3.5$
We know, in 3 round trips the displacement will be zero.
In $0.5$ round, the farmer will reach diametrically opposite to his initial position.
$\therefore$ Displacement = $AC=\sqrt{(A{B}^2+B{C}^2)}=\sqrt{({100}^2+{100}^2)}=10\sqrt{2}m$

Q 3. Which of the following is true for displacement?

(a) It cannot be zero.

(b) Its magnitude is greater than the distance traveled by the object.

Answer:

(a) The first statement is false. Because displacement can be zero when the initial point coincides with the final point.

(b) The second statement is false. The magnitude of displacement can never be greater than the distance travelled by the object. It can be either equal or less.

Q 2. Under what condition(s) is the magnitude of the average velocity of an object equal to its average speed?

Answer:

When the total distance traveled by the object is equal to the displacement, the magnitude of the average velocity will be equal to the average speed. Average speed is the total distance upon the time taken, whereas average velocity is the total displacement upon time taken.

Q 3. What does the odometer of an automobile measure?

Answer:

Odometer is a device that measures the total distance traveled by automobile.

Q 4. What does the path of an object look like when it is in uniform motion?

Answer:

An object is having a uniform motion if it covers equal distance in equal interval of time (which implies speed is constant!). So the path can be straight or curved.

For eg. Consider a circular path. For understanding purposes, divide the circumference of the circle in six equal parts each subtending ${60}^{\circ }$ at the centre. The object covers each equal part in equal amount of time. Hence, by definition, this object is in uniform motion.

Q 5. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is , $3\times {10}^{8}m{s}^{-1}$.

Answer:

Given, the signal travels at the speed of light, $v=3\times {10}^{8}m{s}^{-1}$ .

Time taken by the signal = $5mins=5\times 60s=300s$

Let the distance of the spaceship from the ground station be $Dm$

We know, $Speed=\frac{Distancetravelled}{Timetaken}$

$⟹v=\frac{D}{t}$

$⟹D=v\times t=3\times {10}^8\times 300$

$⟹D=9\times {10}^{10}m$

Therefore, the distance of spaceship from the ground station is $9\times {10}^{10}m$

Q.2 A bus decreases its speed from 80 km h^-1 to 60 km h^-1 in 5 s. Find the acceleration of the bus.

Answer:

(We know, $1km=1000m;1hr=3600s$ )

Given, Initial speed of the bus, $u$ = $80km{h}^{-1}=\frac{80\times 1000}{3600}=\frac{200}{9}m{s}^{-1}$

The final speed of the bus, $v$ = $60km{h}^{-1}=\frac{60\times 1000}{3600}=\frac{100}{6}m{s}^{-1}$

Time is taken, $t=5s$

We know, $v=u+at$

$⟹\frac{100}{6}=\frac{200}{9}+a(5)$

$⟹5a=\frac{900-1200}{6\times 9}=\frac{-300}{6\times 9}$

$⟹a=-\frac{100}{9}=-1.11m{s}^{-2}$

The negative sign implies retardation.

Therefore, the acceleration of the bus is $-1.11m{s}^{-2}$

Or, the retardation(de-acceleration) of the bus is $1.11m{s}^{-2}$

Q 3 . A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h^-1 in 10 minutes. Find its acceleration.

Answer:

(We know, $1km=1000m;1hr=3600s$ )

Given, The train starts from rest. Hence, the initial speed of the train = $0km{h}^{-1}=0m{s}^{-1}$

Final speed of the train = $40km{h}^{-1}=\frac{40\times 1000}{3600}=\frac{100}{9}m{s}^{-1}$

Time taken, $t=10min=10\times 60s=600s$

We know, $v=u+at$

$⟹\frac{100}{9}=0+a(600)$

$⟹a=\frac{100}{9\times 600}=\frac{1}{6\times 9}$

$⟹a=\frac{1}{54}=0.0185m{s}^{-2}$

Therefore, the acceleration of the train is $0.0185m{s}^{-2}$

Topic 7.4 Graphical Representation of Motion

Q 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?

Answer:

Distance-time graph is the plot of distance travelled by an object along x-axis against time along y-axis.

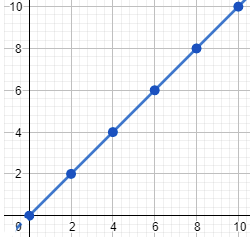
For the uniform motion of an object, the distance-time graph is a straight line with a constant slope.

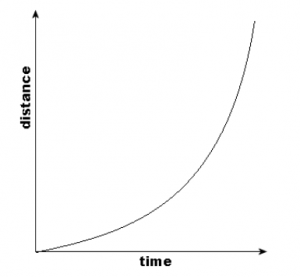
For non-uniform motion of an object, the distance-time graph is a curved line with an increasing or decreasing slope.

Q2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?

Answer:

If the distance-time graph of an object is a straight line parallel to the time axis, it means that the distance of the object is the same from its initial position at any point of time. This implies that the object is not moving and is at rest.

Q3. What can you say about the motion of an object if its speedtime graph is a straight line parallel to the time axis?

Answer:

If the speed-time graph of an object is a straight line parallel to the time axis, it means that the speed of the object is not changing with time. Hence the speed of the object is constant. This also implies that the acceleration of the object is zero.

Q4. What is the quantity which is measured by the area occupied below the velocity-time graph?

Answer:

The area occupied below the velocity-time graph denotes the total distance travelled by an object in the given time frame.

We know,

$$\begin{gathered} Speed=\frac{Distance}{Time} \\ ⟹Distance=Speed\times Time \end{gathered}$$

Topic 7.5 Equations of motion by graphical method

Q1.(a) A bus starting from rest moves with a uniform acceleration of 0.1 m s^-2 for 2 minutes. Find the speed acquired

Answer:

Given, The bus starts from rest. Hence, the initial speed of the bus = $0m{s}^{-1}$

Acceleration of the bus, $a$ = $0.1m{s}^{-2}$

Time is taken, $t=2min=2\times 60s=120s$

(a) We know, $v=u+at$

$⟹v=0+(0.1)(120)=12m{s}^{-1}$

Therefore, the speed acquired by the bus is $12m{s}^{-1}$

Q1.(b) A bus starting from rest moves with a uniform acceleration of 0.1 m s^-2 for 2 minutes. Find the distance travelled.

Answer:

Given, The bus starts from rest. Hence, the initial speed of the bus, u = $0m{s}^{-1}$

Acceleration of the bus, $a$ = $0.1m{s}^{-2}$

Time taken, $t=2min=2\times 60s=120s$

(b) We know, $s=ut+\frac{1}{2}a{t}^2$

$⟹s=0(120)+\frac{1}{2}(0.1)(120{)}^2$

$⟹s=\frac{1}{2}(0.1)(14400)$

$⟹s=720m$

Therefore, the distance travelled by bus is $720m$

Q2. A train is travelling at a speed of 90 km h^-1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s^-2. Find how far the train will go before it is brought to rest.

Answer:

(We know, $1km=1000m;1hr=3600s$ )

Given, Initial speed of the train, $u$ = $90km{h}^{-1}=\frac{90\times 1000}{3600}=25m{s}^{-1}$

Acceleration of the train, $a=-0.5m{s}^{-2}$ (Negative sign implies retardation)

Since, the train has to be brought to rest, final speed of the train, $v$ = $0m{s}^{-1}$

We know, $v^2=u^2+2as$

$⟹0^2={25}^2+2(-0.5)s$

$⟹0=625-s$

$⟹s=625m$

Therefore, the train travels a distance of $625m$ before coming to rest.

Q3. A trolley, while going down an inclined plane, has an acceleration of 2 cm s^-2 . What will be its velocity 3 s after the start?

Answer:

Given, The trolley starts from rest. Hence, the initial speed of the trolley, $u$ = $0cm{s}^{-1}$

Acceleration of the trolley, $a$ = $2cm{s}^{-2}$

Time is taken, $t=3s$

We know, $v=u+at$

$⟹v=0+(2)(3)=6cm{s}^{-1}$

Therefore, the velocity of the trolley after 3 sec is $6cm{s}^{-1}$

Q4. A racing car has a uniform acceleration of 4 m s^-2 . What distance will it cover in 10 s after start?

Answer:

Given, Initial speed of the racing car, u = $0m{s}^{-1}$

Acceleration of the car, $a$ = $4m{s}^{-2}$

Time taken, $t=10s$

We know, $s=ut+\frac{1}{2}a{t}^2$

$⟹s=0(10)+\frac{1}{2}(4)(10{)}^2$

$$\begin{gathered} ⟹s=2(100) \\ ⟹s=200m \end{gathered}$$

Therefore, the distance travelled by the racing car in $10s$ is $200m$

Q 5. A stone is thrown in a vertically upward direction with a velocity of $5m{s}^{-1}$ . If the acceleration of the stone during its motion is $10m{s}^{-2}$ in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?

Answer:

Taking upward direction as positive (+) direction:

Given,

$u=5m{s}^{-1}$

$a=-10m{s}^{-2}$ (This is due to gravitational force!)

The stone will move up until its velocity becomes zero.

$\therefore v=0m{s}^{-1}$

We know, $v^2=u^2+2as$

$⟹0^2=5^2+2(-10)s$

$$\begin{gathered} ⟹20s=25 \\ ⟹s=1.25m \end{gathered}$$

Therefore, the stone reaches to a height of $1.25m$

Now,

We know, $v=u+at$

$$\begin{gathered} ⟹0=5+(-10)t \\ ⟹t=0.5s \end{gathered}$$

Therefore, the time taken by the stone to reach the maximum height is $0.5s$ .

NCERT Solutions for Class 9 Science Chapter 7 Motion: Solved Exercise Questions-

Q 1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?

Answer:

Given, Diameter of the circular track = $200m$

$\therefore$ The circumference of the circular track, $d=2\pi \frac{D}{2}=200\pi m$

The athlete completes one round of a circular track in 40 s.

$\therefore$ Speed of the athlete = $u=\frac{200\pi m}{40s}=5\pi m{s}^{-1}$

In $t=2min20s=140s$ ,

Distance travelled by the athlete = $Speed\times time=(5\pi )\times (140)$

$=5\times \frac{22}{7}\times 140=2200m$

Also, number of rounds the athlete will complete in $140s$ = $\frac{140}{40}=3.5$

Therefore, the final position of the athlete after $140s$ will be diametrically opposite to his initial point.

(3 complete rounds and one half round.)

Hence, displacement of the athlete = magnitude of diameter of the circle =200m

Q2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging

(a) from A to B and

(b) from A to C?

Answer:

Given,

(a) Distance between A and B = $300m$

Time taken to reach from A to B = $2min30s=150s$

$\therefore$ Average speed from A to B = $\frac{Distance}{Time}=\frac{300}{150}=2m{s}^{-1}$

And, Average velocity from A to B = $\frac{Displacement}{Time}=\frac{300}{150}=2m{s}^{-1}$

(In this case, average speed is equal to the average velocity)

(b) Distance travelled from A to reach C = $AB+BC=300+100=400m$

And, Displacement from A to C = $AC=300-100=200m$

Also, time taken to reach C from A = $2min30s+1min=(150+60)s=210s$

$\therefore$ Average speed from A to C = $\frac{Distance}{Time}=\frac{400}{210}=1.90m{s}^{-1}$

And, Average velocity from A to C = $\frac{Displacement}{Time}=\frac{200}{210}=0.95m{s}^{-1}$

(In this case, average speed is not equal to the average velocity)

Q 3. Abdul, while driving to school, computes the average speed for his trip to be $20km{h}^{-1}$ . On his return trip along the same route, there is less traffic and the average speed is $30km{h}^{-1}$ . What is the average speed for Abdul’s trip?

Answer:

Given, Average speed while going to school, $v_1=20km{h}^{-1}$

And Average speed while returning back from school, $v_2=30km{h}^{-1}$

Let the distance between starting point and school be $xm$

And time taken by Abdul during the two trips be $t_{1}sand{t}_{2}s$

We know, $Speed=\frac{Distance}{Time}$

$\therefore v_1=\frac{x}{t_1}=20$

And, $\therefore v_2=\frac{x}{t_2}=30$ -(i)

Now, Total distance that Abdul covers = $x+x=2x$

And total time Abdul takes to cover this distance = $t_1+t_2$

$$\begin{gathered} \therefore v_{avg}=\frac{2x}{t_1+t_2} \\ =\frac{2x}{\frac{x}{20}+\frac{x}{30}} \\ =\frac{60\times 2x}{5x} \\ =24m{s}^{-1} \end{gathered}$$

Therefore, the average speed for Abdul's trip is $24m{s}^{-1}$

(Note: $\frac{20+30}{2}=25m{s}^{-1}\ne 24m{s}^{-1}$ )

Q 4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of $3.0m{s}^{-2}$ for 8.0 s. How far does the boat travel during this time?

Answer:

Given, The motorboat starts from rest. Hence, initial speed of the motorboat, u = $0m{s}^{-1}$

Acceleration of the motorboat, $a$ = $3.0m{s}^{-2}$

Time taken, $t=8s$

We know, $s=ut+\frac{1}{2}a{t}^2$

$⟹s=0(8)+\frac{1}{2}(3)(8{)}^2$

$⟹s=\frac{1}{2}(3)(64)$

$⟹s=96m$

Therefore, the distance travelled by the motorboat is $96m$

Q 5. A driver of a car travelling at 52 km h^-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h^-1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?

Answer:

The initial speed $=52\times \frac{5}{18}=14.4\frac{m}{s}$

After 5 sec the car stops

The graph is represented by the blue line ( x-axis is time and the y-axis is speed)

For the car with 3Kmh -1 . Initial speed $=3\times \frac{5}{18}=0.833\frac{m}{s}$ . The graph which is represented by the golden line

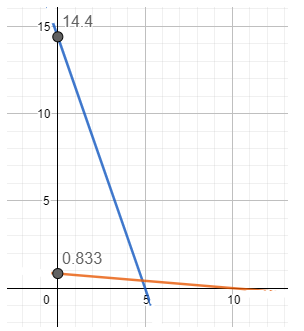
The area covered by the blue graph is greater than the golden graph so the car with 15 m/s initial velocity travells large distance.

Q 6. (a) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

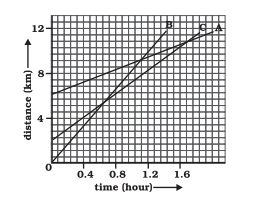
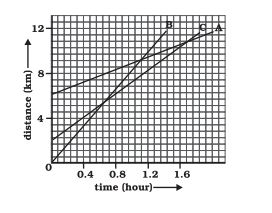
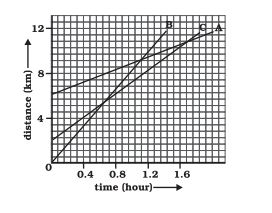
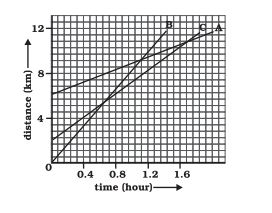
Which of the three is travelling the fastest?

Answer:

Given is a distance-time graph. The slope of this graph gives us speed. Hence, the graph with the highest slope will have the highest speed.

Since B has the highest slope(inclination), it travels the fastest.

Q 6. (b) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

Are all three ever at the same point on the road?

Answer:

Given is a distance-time graph. Any point on the curve will give the distance of object from O. Since there is no intersection point of all the three graphs, they never meet at the same point on the road.

(Although any two of them do meet at some point on the road!)

Q 6.(c) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

How far has C travelled when B passes A?

Answer:

Given is a distance-time graph. Any point on the curve will give the distance of object from O. To find how far C has travelled when B passes A, draw a perpendicular from the intersection point of A and B on time axis. The point where it intersects on the C graph, from C draw a perpandicular to y axis . Therefore, distance travelled by C will be (Final distance from O - Initial distance from O)

Therefore, C has traveled 6.5 km when B passes A.

Q 6. (d) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

How far has B travelled by the time it passes C?

Answer:

Given is a distance-time graph. The graph of B and C intersect at a point whose y-coordinate is 5. Hence, B has travelled $5km$ by the time it passes C.

Q 7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s^-2 , with what velocity will it strike the ground? After what time will it strike the ground?

Answer:

Considering downward direction as positive direction.

Given, Height from which ball is dropped, $s=20m$

Acceleration of the ball, $a$ = $10m{s}^{-2}$

Initial velocity, $u=0m{s}^{-1}$

(i) We know, $v^2=u^2+2as$

$⟹v^2=0^2+2(10)(20)$

$⟹v^2=400$

$⟹v=20m{s}^{-1}$ (In downward direction)

Therefore, the ball will strike the ground with a velocity of $20m{s}^{-1}$

(ii) Now, we know, $v=u+at$

$$\begin{gathered} ⟹20=0+10t \\ ⟹t=2s \end{gathered}$$

Therefore, the ball reaches the ground in $2s$ .

Note: $v=-20m{s}^{-1}$ was rejected because in this case, the negative sign implies the velocity in upward direction, which is opposite to the direction of the motion of the ball(before collision).

Q 8.(a) The speed-time graph for a car is shown is Figure:

Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.

Answer:

Given is a speed-time graph. The area under the curve will give the distance travelled by the car.

In time $t=4s$ , the distance travelled by the car will be equal to the area under the curve from $x=0tox=4$

Considering this part of the graph as a quarter of a circle whose radius = 4 unit.

Therefore, required area = $\frac{1}{4}\pi r^2=\frac{1}{4}\pi (4{)}^2=12.56m$

Therefore, distance the car travelled in the first 4 seconds is $12.56m$

Q 8. (b) The speed-time graph for a car is shown is Figure:

Which part of the graph represents uniform motion of the car?

Answer:

In uniform motion, the speed of car will become constant which is represented by line parallel to the time axis. In the given figure, the straight line graph from $t=6stot=10s$ represents the uniform motion of the car.

Q 9. (a) State which of the following situations are possible and give an example for each of these: an object with a constant acceleration but with zero velocity

Answer:

(a) The given situation is possible.

When an object is thrown upwards (under gravity only), it reaches to a maximum height where its velocity becomes zero. However, it still has an acceleration acting in the downward direction (acceleration due to gravity).

Note: This is possible for a given point of time, however, it is not possible for a period of time.

Q 9.(b) State which of the following situations are possible and give an example for each of these: an object moving with an acceleration but with uniform speed.

Answer:

(b) The given situation is possible.

An object moving in a circular path with uniform speed, i.e covering equal distance in equal amount of time is still under acceleration. Because, the velocity keeps on changing due to continuous change in the direction of motion. Therefore, circular motion is an example of an object moving with an acceleration but with uniform speed.

Q 9. (c) State which of the following situations are possible and give an example for each of these: an object moving in a certain direction with an acceleration in the perpendicular direction.

Answer:

(c) The given situation is possible.

For an object moving in a circular path with constant speed, the direction of its velocity at any point will be tangential to that point. However, its acceleration will be directed radially inwards. (Constant speed but still having an acceleration - Due to continuous change in direction.)

Q 10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.

Answer:

Given, Radius of the circular orbit = $42250km$

$\therefore$ Circumference of the orbit = $2\pi r=2.\frac{22}{7}.(42250)=265571.4km$

The satellite takes 24 hours to revolve around the earth.

We know, $Speed=\frac{Distance}{Time}$

$$\begin{gathered} Speed=\frac{265571.4}{24} \\ =11065.4km{h}^{-1} \\ =\frac{11065.4}{3600}km{s}^{-1} \\ =3.07km{s}^{-1} \end{gathered}$$

Therefore, the speed of the artificial satellite is $3.07km{s}^{-1}$