NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

Mathematics requires numbers as essential elements to symbolise everyday quantities, together with measurements and values. Different number types receive status classification within the number system through their inherent properties. The exploration in this chapter covers the classification of numbers through natural numbers and whole numbers, integers, rational numbers and irrational numbers. The different number classifications enable us to carry out mathematical processes effectively when solving real-world problems. Students must practice all the topics of the Number System to score better. Along with this, the NCERT class 9th maths notes present detailed information about mathematical principles, and the NCERT notes are examined to strengthen essential formulas, together with fundamental theorems, while reviewing them.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

1. NCERT Notes Class 9 Maths Chapter 1 Number Systems
2. How to Find a Rational Number Between Two Numbers?
3. Representation of Real Numbers on the Number Line:
4. Identities Related to Square Roots
5. Rationalising the Denominator
6. Laws of Exponents for Real Numbers
7. Class 9 Chapter Wise Notes
8. NCERT Solutions for Class 9
9. NCERT Exemplar Solutions for Class 9
10. NCERT Books and Syllabus

NCERT Notes Class 9 Maths Chapter 1 Number Systems

A number is a mathematical entity used for counting, measuring, and labelling. Mathematical operations of addition, subtraction, multiplication and division work with the help of numbers. Numbers exist in multiple categories according to their nature, featuring natural numbers, whole numbers, integers, rational numbers and irrational numbers.

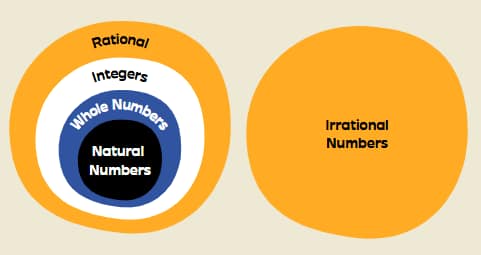
Natural numbers

These are the numbers that start from the count of one to infinity. The natural numbers can be represented by “N”. Natural numbers are always positive. Multiplication and addition operations between natural numbers produce only natural numbers as results

Example of Natural Numbers: N = {1, 2, 3, 4, 5, 6……}

Whole numbers

These include all natural numbers but start from the count of zero. The whole numbers can be represented by “W”. All natural numbers are whole numbers, except 0, which is not a natural number but is a whole number.

Example of Whole Numbers: W = { 0, 1, 2, 3, 4, 5, 6…...}

Integers

These are the numbers that include both positive and negative numbers along with zero. Although Zero is an integer, it exists outside the boundaries of positive and negative numbers, which means it is neither positive nor negative.

Example of Integers: {…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……}

Rational numbers

These are the numbers that are any real number and can be expressed in the form $\frac{p}{q}$ of R where the denominator $q\ne 0$. It is represented by "Q". It is noted that every integer number is a rational number. The decimal expansion of these numbers is either repeating or terminating.

Example of Rational Numbers: $\frac{1}{2}$, $\frac{3}{4}$, $\frac{-7}{8}$, $0.3333...$, etc.

On division of $p$ by $q$, two main things happen – either the remainder becomes zero or never becomes zero, and we get a repeating string of remainders.

Case (i): The Remainder Becomes Zero

This is the case of terminating numbers, which means that after dividing the numbers, the remainder comes as 0.

Example: $\frac{7}{8}$ = 0.875

When the numbers are divided, the remainder is 0. And therefore called a terminating number.

Case (ii): The Remainder Never Becomes Zero

This is the case of repeating numbers, which means the remainders repeat after a certain stage, forcing the decimal expansion to go on forever.

Example: $\frac{10}{3}$ = 3.3333….

When the numbers are divided, we have a repeating block of digits in the quotient, and the remainders are not equal to zero.

How to Find a Rational Number Between Two Numbers?

The calculation of an average between two numbers $a$ and $b$ produces a rational number. It means:

Rational number = $\frac{\text{a + b}}{2}$

Example: Find a rational number between 1 and 2.

Solution: According to the formula, take the average of the numbers:

Rational Number = $\frac{1+2}{2}=\frac{3}{2}$

To find another rational number, repeat the same process, hence, it means that there are infinitely many rational numbers between any two given rational numbers.

Irrational Numbers

These are the numbers that cannot be expressed in the form $\frac{p}{q}$ of R where the denominator $q\ne 0$. The decimal expansion of these numbers is non-repeating and non-terminating. Like rational numbers, there are infinitely many irrational numbers, too.

Example of Irrational Numbers: $\surd 2$,$\surd 3$, $\pi$, $0.34343...$, etc.

Real Numbers

These numbers are defined as those that can be represented on the number line. They are further divided into two parts such as rational and irrational numbers. They can be represented as $R$.

Note: Each real number finds its distinct position as a point along the number line. Furthermore, the number line contains unique real numbers at every one of its points.

Representation of Real Numbers on the Number Line:

The number line provides a visual representation scheme that displays both rational and irrational numbers among the real numbers. The number line serves to demonstrate how numbers are positioned relative to each other.

Steps to Plot an Irrational Number on a Number Line:

• Construct a horizontal line which uses zero as its base point.
• Put the negative numbers on the left and the positive ones on the right.
• Locate the two square numbers that contain the provided irrational number.
• Construct a right-angled triangle using Pythagoras' theorem to represent the given irrational number through the hypotenuse.
• Measure the hypotenuse of the triangle with a compass.
• Set your compass pointer to 0 on the number line, then draw a mark at the measured distance.
• The necessary irrational number is indicated by the marked point on the number line.
• Label it accordingly.

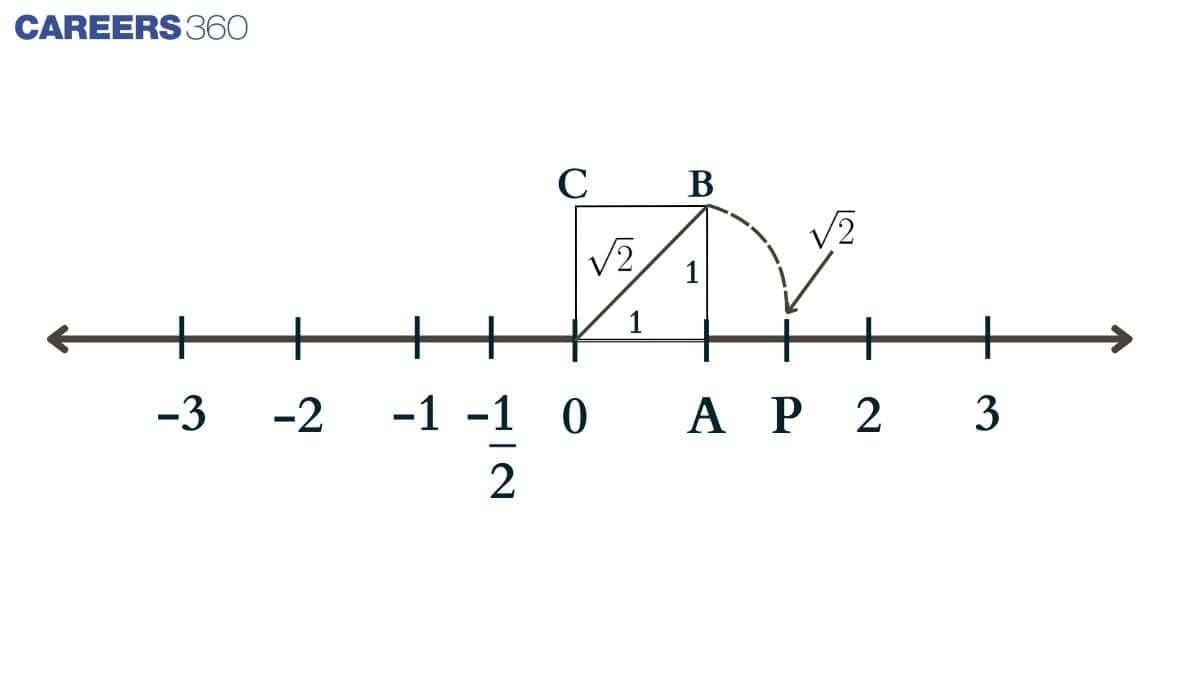
Example: Locate √2 on the number line.

Solution: Steps to solve the problem:

1. Draw a horizontal number line.
2. Mark the integers -3, -2, -1, 0, 1, 2, 3, etc., keeping equal spacing between them.
3. √2 must lines between 1 and 2.
4. At 1, draw a perpendicular line of 1 unit upwards.
5. Join the new point to 0 to form a right-angled triangle having base and height equal to 1.
6. Since right right-angled triangle is formed, check the hypotenuse with Pythagoras' theorem.
7. Take a compass and set its length to the hypotenuse of the triangle.
8. Place the compass pointer at 0 and draw an arc on the number line.
9. The intersection of the arc and the number line gives the required point of √2.
   
   

Key Points

(i) The sum or difference of a rational number and an irrational number is irrational.

(ii) The product or quotient of a non-zero rational number with an irrational number is irrational.

(iii) If we add, subtract, multiply or divide two irrationals, the result may be rational or Irrational.

Identities Related to Square Roots

The fundamental identities of square roots enable both the simplification of expressions and the solution of equations. Several important identities exist for square roots, which are as follows:

• $\sqrt{ab}=\sqrt{a}\times \sqrt{b}$
  
  
• $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
  
  
• $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$
  
  
• $(a+\sqrt{b})(a-\sqrt{b})=a^2-b$
  
  
• $(\sqrt{a}+\sqrt{b})(\sqrt{c}+\sqrt{d})=\sqrt{ac}+\sqrt{ad}+\sqrt{bc}+\sqrt{bd}$
  
  
• $(\sqrt{a}+\sqrt{b}{)}^2=a+2\sqrt{ab}+b$

Rationalising the Denominator

Converting an expression containing irrational denominators into equivalent fractions with rational denominators represents the process of denominator rationalisation. To achieve rationalisation, we apply multiplication on both the numerator and denominator by an acceptable conjugate or irrational factor until the square root disappears.

Example: Rationalize $\frac{1}{\sqrt{5}}$

Solution: $\frac{1}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{5}}{5}$

$\frac{2}{3+\sqrt{2}}\times \frac{3-\sqrt{2}}{3-\sqrt{2}}=\frac{6-2\sqrt{2}}{7}$

Laws of Exponents for Real Numbers

When a number is multiplied repeatedly, it is represented by an exponent, also known as a power. For real numbers, the exponent laws listed below are applicable:

• $a^m\times a^n=a^{m+n}$
  
  
• $\frac{a^m}{a^n}=a^{m-n},a\ne 0$
  
  
• $(a^m{)}^n=a^{m\times n}$
  
  
• $a^m\times b^m=(a\times b{)}^m$

1. Let a > 0 be a real number. Let m and n be integers such that m and n have no common factors other than 1, and n > 0.
Then,

$a^{\frac{m}{n}}=\sqrt[n]{a^m}={\left(\sqrt[n]{a}\right)}^m$

2. Let a > 0 be a real number and n a positive integer. Then,

$\sqrt[n]{a}=b$ if $b^n=a$ and b > 0

$\sqrt[n]{a}=a^{\frac{1}{n}}$

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Syllabus for Class 9
• NCERT Books for Class 9