NEET/JEE Coaching Scholarship
ApplyGet up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes
A linear equation in two variables is an important concept in mathematics. It helps to establish the equations with two variables, and the relation between these variables will be defined with the help of mathematical operators like addition, subtraction, multiplication and division. This equation generally generates a straight line. A linear equation can have one or two variables. A linear equation has variables with the highest degree or power of the variable being one. The degree of the variable is also known as an exponent. It helps to solve the mathematical problem by creating equations. It is used to calculate the distance, speed, and time of an object. It helps to convert the problem into a mathematical equation. It is also used to solve geometry-related problems like lines, parabolas, etc.
This Story also Contains
- NCERT Class 9 Maths Chapter 4 Linear Equations in Two Variables: Notes
- Class 9 Chapter Wise Notes
- NCERT Solutions for Class 9
- NCERT Exemplar Solutions for Class 9
- NCERT Books and Syllabus
A linear equation can be in one variable or two variables, and these notes cover what is linear equation? Linear equations in one and two variables, their examples and graphical representation. CBSE Class 9 chapter Linear equation in two variables includes all the topics and their examples in these notes. Students must practice all the topics of Linear equation and their examples from the NCERT Exemplar Solutions for Class 9 Maths Chapter 4 Linear Equation in Two Variables. Our Subject Matter Experts designed these NCERT class 9th maths notes in an understandable language. NCERT notes contain all the related study material for classes 9 to 12.
NCERT Class 9 Maths Chapter 4 Linear Equations in Two Variables: Notes
Linear Equation in One Variable: An equation that has one variable with a degree of one is called a linear equation in one variable.
The standard form of a linear equation in one variable is ax + b = 0, where a is not equal to zero.
Example: 2x + 3 = 0, 4x = 1
Linear Equation in Two Variables: An evaluation that has two variables with a degree of one is known as a linear equation in two variables.
The standard form of a linear equation in two variables is ax + by + c = 0, where a and b are not equal to zero.
Example: 3x + 2y = 5, 2a + 3b + 4 = 0
Establish a Linear Equation in Two Variables
The linear equation in two variables can be created by assuming the variables with the values as given in the example.
Example: The sum of the cost of a bat and a ball is 12. Write a linear equation in two variables to represent this statement.
Let the bat be represented by x and the ball by y.
According to the statements,
The equation is: x + y = 12
Solution of Linear Equations in Two Variables
The linear equation in two variables has two variables, which consist of two numbers and are known as the solution of the linear equation in two variables.
Some points related to the solution of linear equations in two variables:
1. Solution can be determined by the assumption method, and according to this method value of one variable is assumed, and this variable is replaced with this value and proceed to find the solution for the other variable.
2. There are many possible solutions for the same linear equation in two variables.
Graphical Representation of a Linear Equation in Two Variables
For any linear equation ax + by + c = 0, the pair of solutions in the form of variables (x, y) can be represented in the coordinate plane. With these coordinate values, the line doesn't always need to cut the coordinate axes.
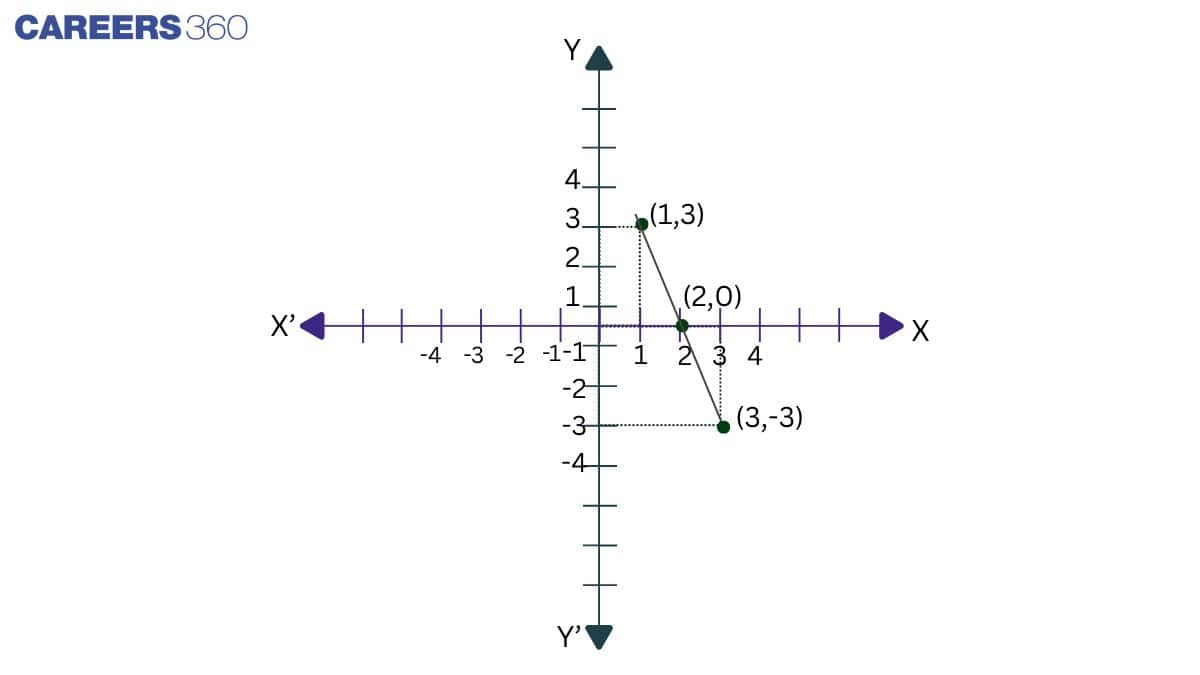
Example: Write four solutions for the equation 3x + y = 6.
| Value of x | Replacing the Value of x in the Equation | Value of y | (x, y) |
| X = 1 | 3(1) + y = 6 | 3 | (1, 3) |
| X = 2 | 3(2) + y = 6 | 0 | (2, 0) |
| X = 3 | 3(3) + y = 6 | -3 | (3, -3) |
The graphical representation for the given coordinates is as follows,
Important Points:
1. Every coordinate in the graphical representation is the solution of a linear equation.
2. In a linear equation in two variables, when any number is added, multiplied, divided or subtracted from both sides of the equation, then the equation will be unaffected.
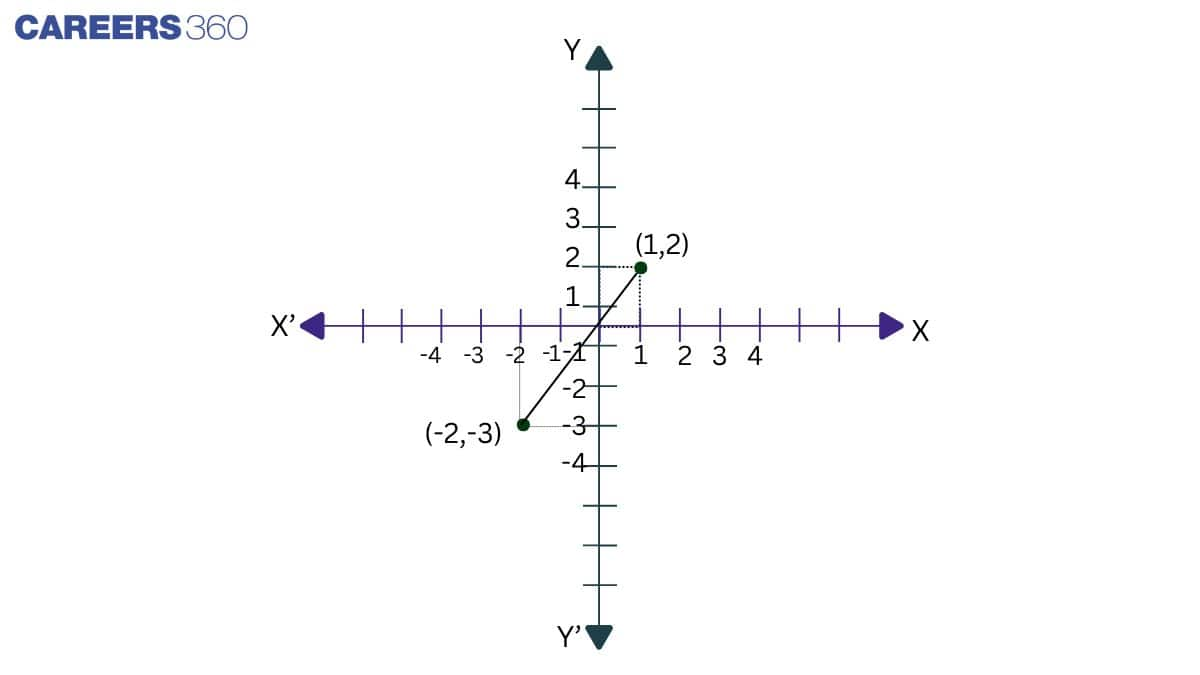
Lines Passing Through the Origin
When a linear equation has a solution coordinate (0, 0), and if these coordinates are represented in the coordinate plane, then these points pass through the origin as shown in the figure:
Lines Parallel to the Coordinate Axes
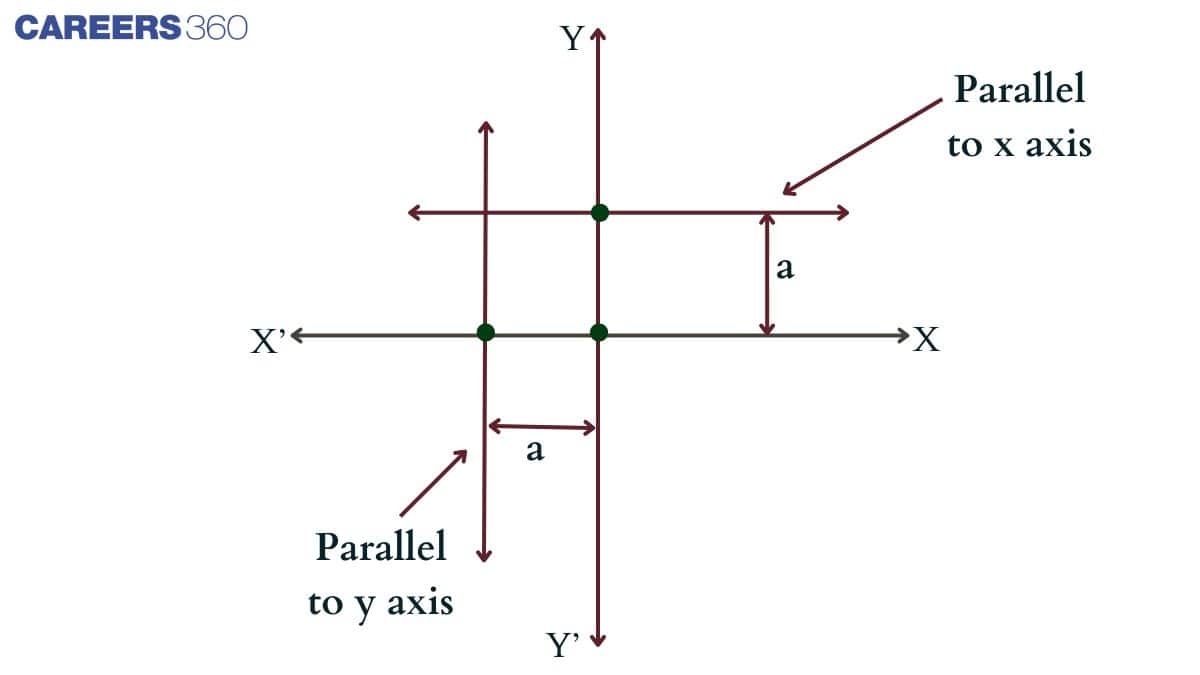
A line is called a parallel line to the x-axis if the equation is in the form of y = a, where a is the distance of the line from the x-axis and a is a constant value. Similarly, A line is called a parallel line to the y-axis if the equation is x = a, where a is the distance of the line from the y-axis and a is a constant value.
Class 9 Chapter Wise Notes
Students must download the notes below for each chapter to ace the topics.
NCERT Notes for Class 9 Maths Chapter 3 - Coordinate Geometry |
NCERT Notes for Class 9 Maths Chapter 4 - Linear Equations in Two Variables |
NCERT Notes for Class 9 Maths Chapter 5 - Introduction to Euclid’s Geometry |
NCERT Notes for Class 9 Maths Chapter 11 - Surface Areas and Volumes |
NEET/JEE Offline Coaching
Get up to 90% Scholarship on your NEET/JEE preparation from India’s Leading Coaching Institutes like Aakash, ALLEN, Sri Chaitanya & Others.
Apply Now
NCERT Solutions for Class 9
Students must check the NCERT solutions for Class 10 Maths and Science given below:
NCERT Exemplar Solutions for Class 9
Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:
NCERT Books and Syllabus
To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.
Also Read
Articles
Upcoming School Exams
Application Date:24 March,2025 - 23 April,2025
Admit Card Date:04 April,2025 - 26 April,2025
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Popular Course After 12th
Study Resources, Applications and Opportunities
NEET Most scoring concepts
Get nowThis ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
TOEFL ® Registrations 2024
ApplyAccepted by more than 11,000 universities in over 150 countries worldwide
News and Notifications
Back to top