Circles Class 9th Notes - Free NCERT Class 9 Maths Chapter 10 Notes - Download PDF

A circle is a closed, geometrical figure with no corners or edges. In the circle, all the points are equidistant from the center. A circle is a two-dimensional, round-shaped figure. There are many real-world examples of circles. Circles are used in architecture, engineering, like civil engineering, electrical engineering, signal processing, and aerospace engineering, computer graphics like for the rotation of objects, in transportation, like the wheels of a car. Apart from this, there are many circular-shaped objects in our daily life, like pizza, coins, buttons, plates, etc.

Don't Miss: Best Courses after 10th | Competitive Exams after 10th

This Story also Contains

1. NCERT Class 9 Maths Chapter 9 Circles: Notes
2. Theorems for Circles and their Chord
3. Class 9 Chapter Wise Notes
4. NCERT Solutions for Class 9
5. NCERT Exemplar Solutions for Class 9
6. NCERT Books and Syllabus

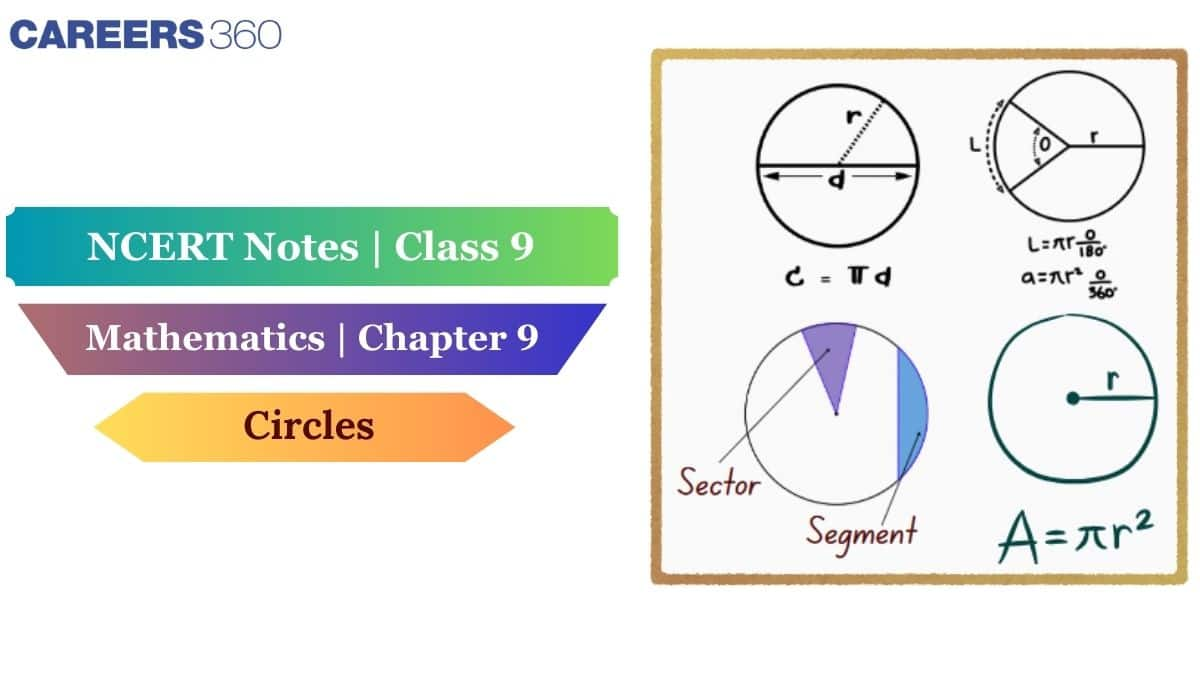
These notes cover the basic definition of circle, arc, radius, tangent and secant, chord, diameter, circumference, segment and sector and related theorems. CBSE Class 9 Chapter 10 also includes a cylindrical quadrilateral. To understand all the topics, students must go through the NCERT class 9th maths notes that include all the definitions, formulas, and examples and all related theorems. Students can download the NCERT notes according to their subjects and standard, which are designed by our Subject Matter Experts.

NCERT Class 9 Maths Chapter 9 Circles: Notes

Circle

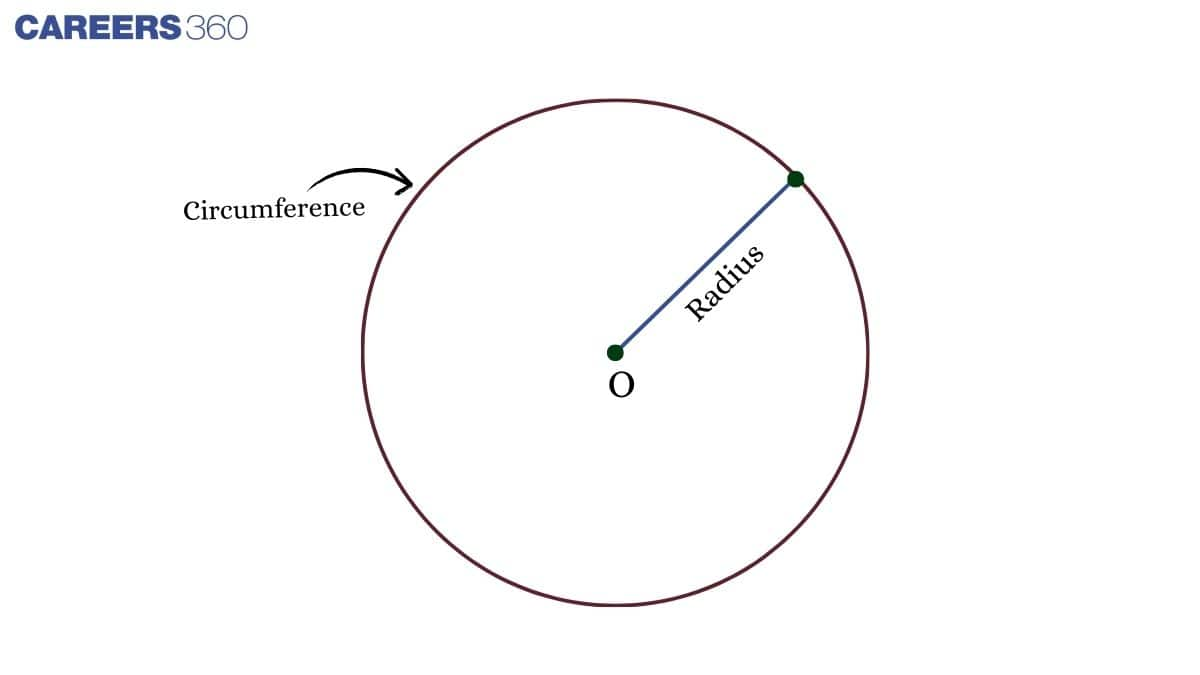
A circle is a two-dimensional closed geometrical figure in which all the points are equidistant from a fixed point, and this fixed point is called the center of the circle. A circle does not have any corners or edges.

Radius

The distance from the center of the circle to a point that lies on the surface of the circle is called the radius, and it is denoted by $r$.

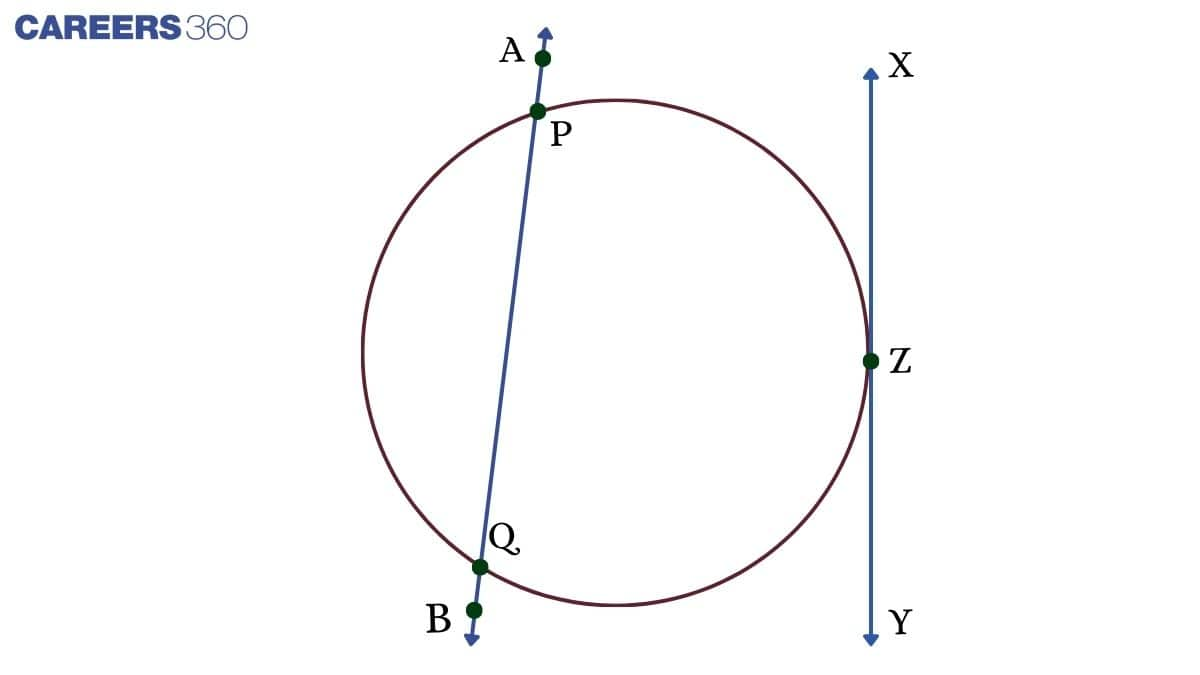
Tangent and Secant:

A line that touches the surface or circumference of the circle at only one point is called the tangent of the circle. A line that cuts the surface of the circle at two points is called the secant of the circle. As shown in the figure, XY is the tangent that touches the circle at one point called Z, and AB is a secant that cuts the circle at two points called PQ.

Chord

A line segment that joins two points of the circumference within the circle is called the chord of the circle.

Diameter

A chord that passes through the center of the circle is called the diameter. The diameter is the longest chord of the circle. Diameter is twice the radius, and it is represented by $d$.

Arc

The small part or segment between the two points of the circumference of the circle is called the arc. The longer arc is called the major arc, and the smaller arc is called the minor arc.

Circumference

The distance covered around the perimeter or the surface of the circle is called the circumference of the circle. The formula for calculating the circumference of the circle is $2\pi r$, where $r$ is the radius of the circle.

Segment and Sector

An area of the circle that is enclosed by an arc and a chord is called the segment. The small segment of the circle is called the minor segment, and the larger segment is called the major segment.
A sector is an area of a circle that is enclosed by two radii of the circle. The small sector of the circle is called the minor sector, and the big sector of the circle is called the major sector of the circle.

Theorems for Circles and their Chord

The important theorems for circles and their chord area are as follows.

Theorem: In a circle, equal chords subtend equal angles at the centre.

In the circle, there are two chords PQ = RS. So PQ = RS need to be proved.
In Δ POQ and ΔROS
PO = OS (Radius)
OQ = OR (Radius)
PQ = RS (Given)
ΔPOQ ≅ ΔROS (By SSS rule)
Therefore, ∠POQ = ∠ROS (Corresponding Parts of Congruent Triangles)

Theorem: The Perpendicular Line From the Centre to a Chord Bisects the Chord.

In the given circle, PR is a chord, and OQ is the perpendicular line drawn from the centre of the circle.
In ΔPOQ and ΔQOR,
OP = OR (Radius)
∠PQO =∠RQO (Both are right angles)
OQ = OQ (common)
Therefore, ΔPOQ ≅ ΔQOR (By RHS rule)
Hence, it is proved that PQ = QR (Corresponding Parts of Congruent Triangles)

Theorem: A Line that Passes Through the Centre and Bisects the Chord is Perpendicular to the Chord.

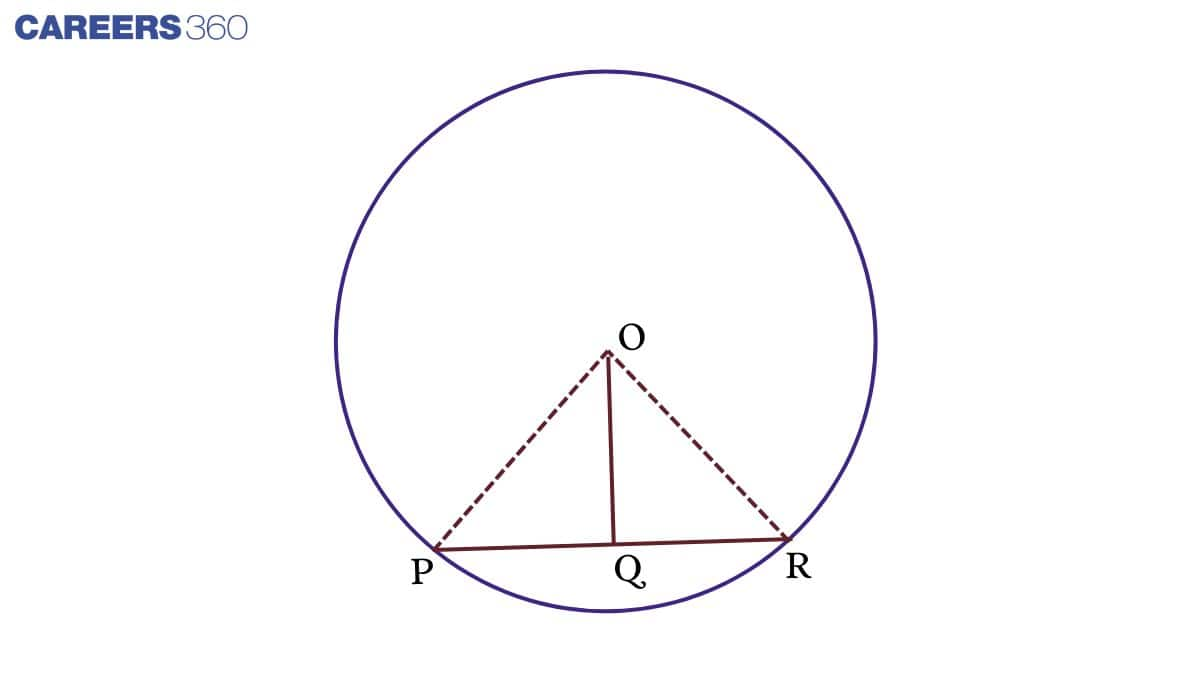
In the figure, OQ is drawn from the centre circle to bisect the chord PR. Therefore, PQ = QR.
From ΔPOQ and ΔQOR,
PQ = QR (Given)
OP = OR (Radius)
OQ = OQ (common)
Therefore, ΔPOQ ≅ ΔQOR (By SSS rule)
⇒∠OQP =∠OQR (Corresponding Parts of Congruent Triangles)
We know that ∠OQP + ∠OQR = 180° (Anles on straight line)
Therefore, ∠OQP + ∠OQR = 90°
Hence, OQ ⊥ PR

Theorem: The Distance Between Two Equal Chords From the Centre is Equal.

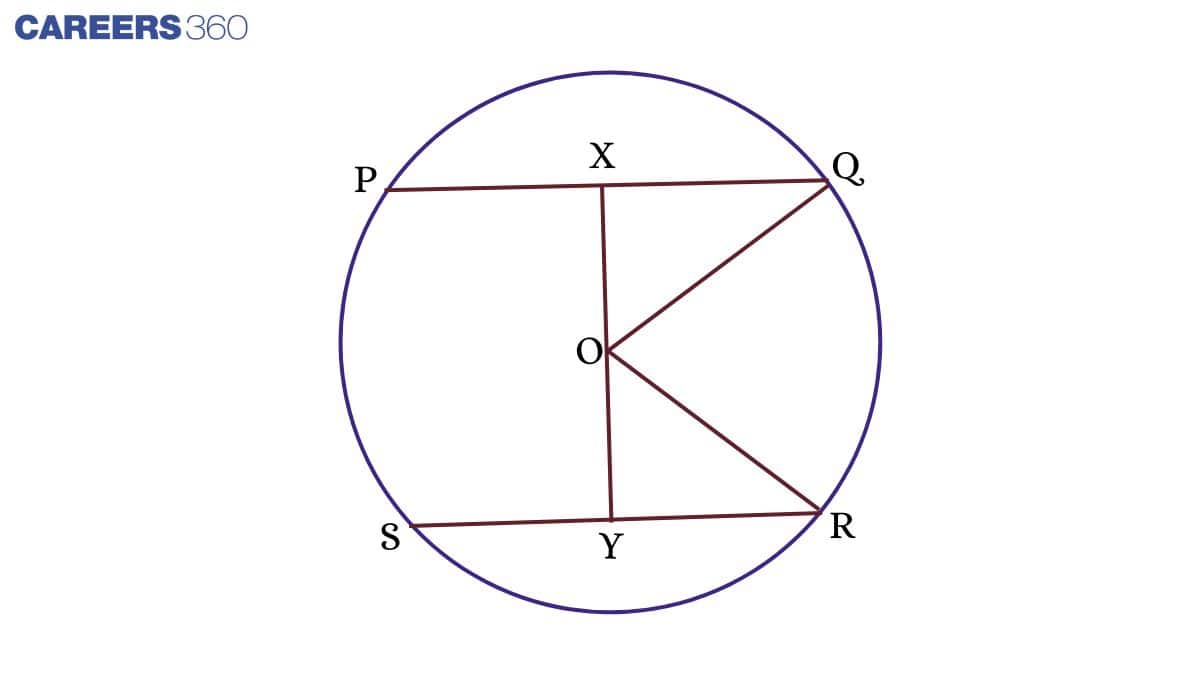
In the figure, PQ = QR, AB = CD, and O is the centre, and join OQ and OR.
Draw, OX⊥PQ, OY⊥SR
In ΔOXQ and ΔYOR,
OQ = OR (Radius)
XQ = YR (PQ = SR and XQ and YR are the halves of PQ and SR, respectively.)
ΔOXQ ≅ ΔYOR (By RHS rule)
Therefore, OX = OY (Corresponding Parts of Congruent Triangles)

Theorem: In a Circle, Chords that are Equidistant From the Centre are Equal.

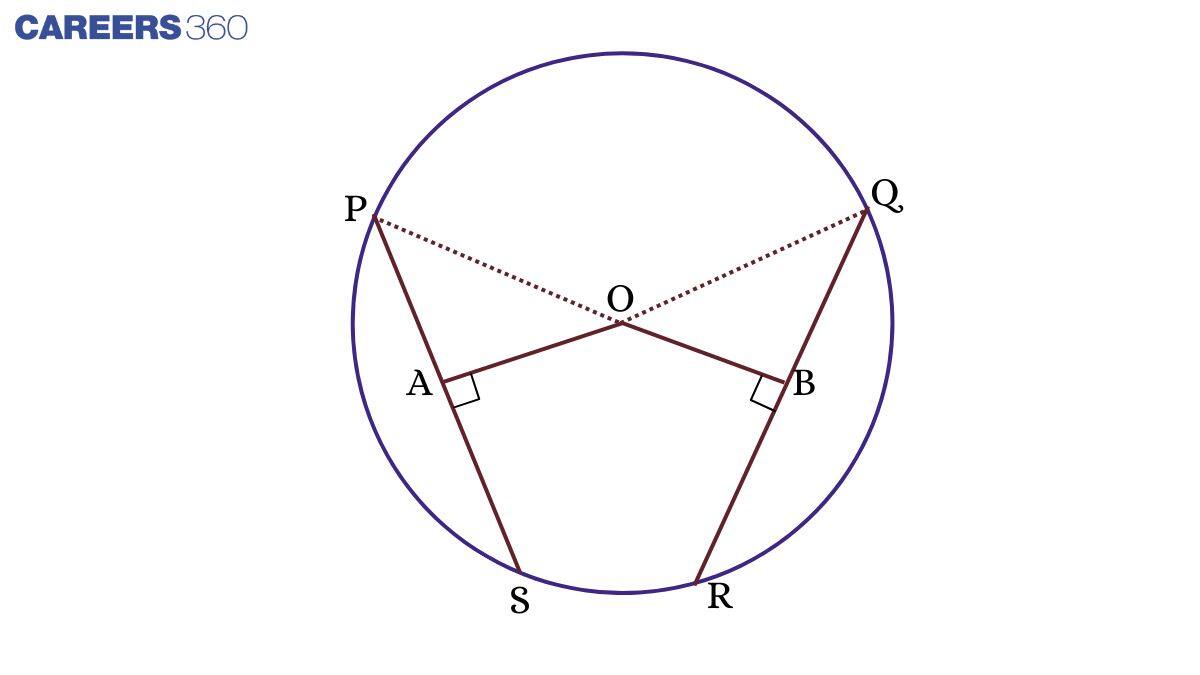
In the figure, OA = OB (Chords PS and QR are equidistant from the centre).
OA ⊥ PS, OB⊥QR
In ΔPOA and ΔQOB
∠POA =∠BOQ (Both 90°)
OP = OQ (Radius)
OA = OB (Given)
ΔPOA ≅ ΔQOB (By RHS rule)
Therefore, PA = QB (Corresponding Parts of Congruent Triangles)
Similarly, AS = BR
Hence, AB = QR

Theorem: The Angle Subtended by an Arc at the Centre is Double the Angle Subtended by it on any Part of the Circle.

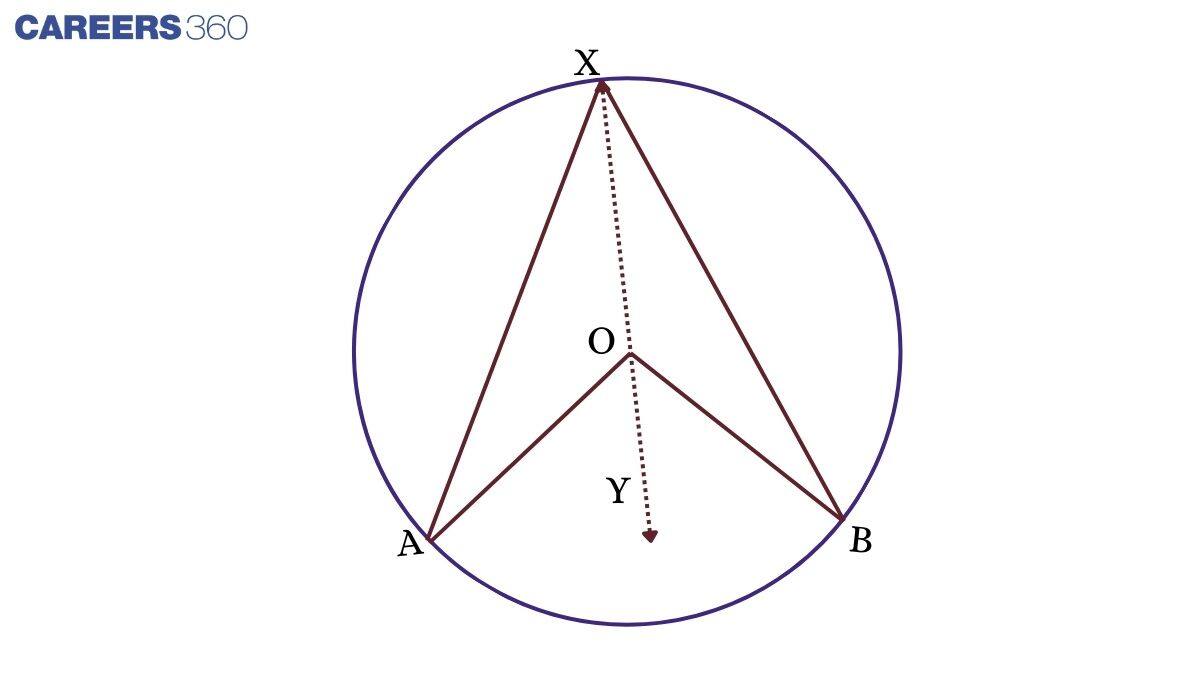
In the figure, O is the centre of the circle, and AB is an arc that subtends ∠AOB at the centre.
Combine XO and extend up to Y.
In ΔBOX,
XO = OB (Radius)
Therefore, ∠OXB = ∠OBX (Isosceles triangle)
Implies ∠YOB = 2∠OXB (Exterior angle of triangle is equals to the sum of 2 interior angles)...... (1)
Similarly,∠YOA = 2∠OXA......(2)
Add equations (1) and (2),
⇒∠YOB + ∠YOA = 2∠OXB + 2∠OXA
⇒∠AOB = 2∠AXB

Theorem: The Angles in the Same Segment of a Circle are Equal.

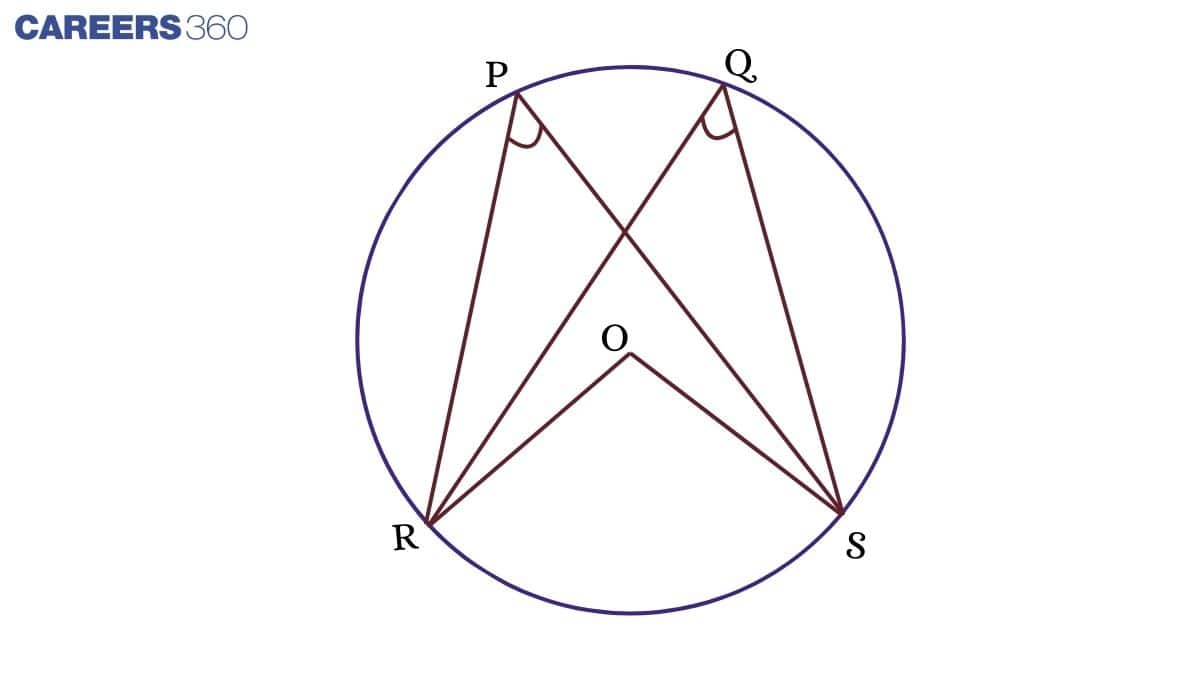
In the figure, O is the centre of the circle, and ∠RPS and ∠RQS are the angles that form the major segment.
Join RO and OS
We know that,
∠ROS = 2∠RPS = 2∠RQS (The angle subtended by an arc at the centre is double the angle subtended by it on any part of the circle)
Therefore, ∠RPS = ∠RQS

Theorem: In a Circle, the Angle Subtended by the Diameter is a Right Angle.

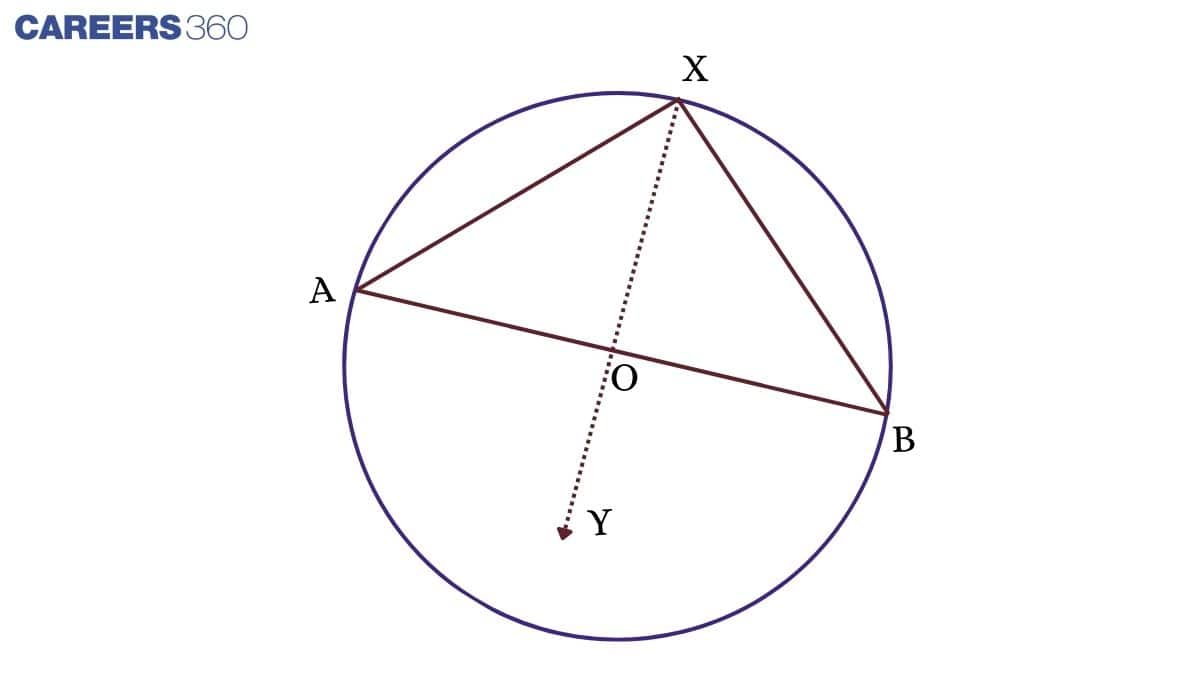
In the figure, O is the centre, and AOB is the diameter of the circle.
∠AXB is the angle for the diameter AB at the circumference.
2∠AXB = ∠AOB = 180° (Angle subtended by arc at the centre is double the angle at any other part)
∠AXB = (1/2) × 180° = 90°

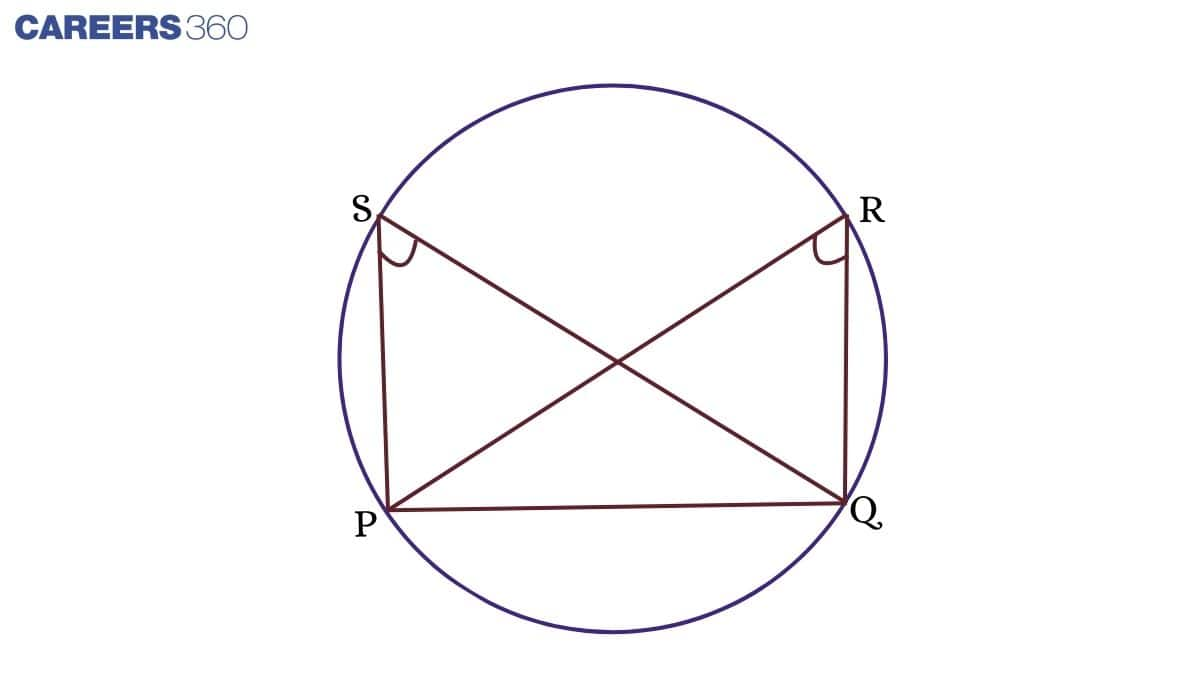
Theorem: A Line Segment that Subtends Equal Angles at Two Other Points.

As shown in the figure, ∠PSQ and ∠PRQ are equal angles as PQRS is concyclic.

Cyclic Quadrilateral

If four vertices of a quadrilateral lie on a circle, then the quadrilateral is called a cyclic quadrilateral.

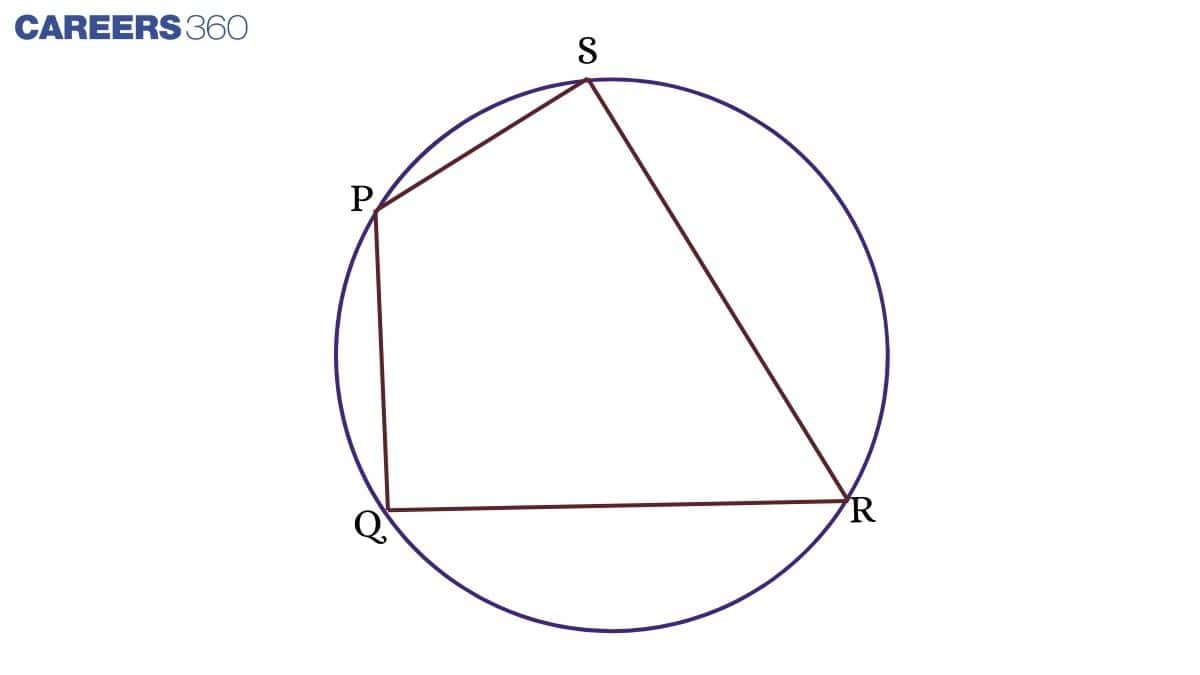
Important Properties of Cyclic Quadrilateral

1. The sum of the opposite angles of a quadrilateral is 180 degrees.
2. The sum of any pair of angles is 180 degrees.

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Syllabus for Class 9
• NCERT Books for Class 9