Coordinate Geometry Class 9th Notes - Free NCERT Class 9th Maths Chapter 3 Notes

Updated on 19 Apr 2025, 01:18 PM IST

Coordinate geometry is the study of geometrical figures that link algebra and geometry by defining points on the axes. The other name of coordinate geometry is analytic geometry or Cartesian geometry. Coordinate geometry helps to determine the distance between two points on the coordinate axes. Coordinate geometry is the study of algebraic equations on a graph. Coordinate geometry is used in many areas, like determining the distance between two places to determine the area of a triangle in the Cartesian plane, determining the midpoint of a line, in GPS, determining the longitude and latitude, forecasting, storms' exact location, etc.

This Story also Contains

NCERT Class 9 Maths Chapter 3 Coordinate Geometry: Notes
Cartesian System
Class 9 Chapter Wise Notes
NCERT Solutions for Class 9
NCERT Exemplar Solutions for Class 9
NCERT Books and Syllabus

Coordinate Geometry

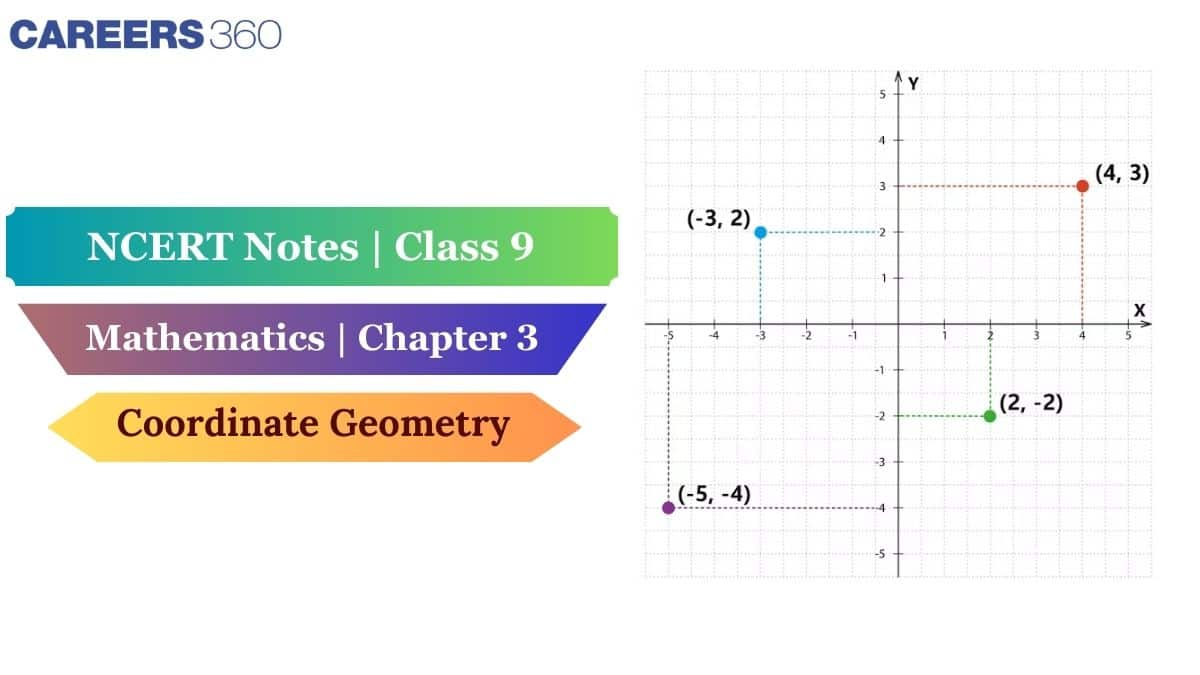
These notes included the definition of coordinate geometry and the Cartesian system. What are the origin, coordinate axes and quadrants? How to plot points and make a line on a graph? CBSE Class 9 chapter Coordinate Geometry includes all the topics and their examples in these notes. Our experts designed NCERT class 9th maths notes that will help the students to understand the concepts easily. NCERT notes cover all the chapters according to the latest syllabus of NCERT.

NCERT Class 9 Maths Chapter 3 Coordinate Geometry: Notes

Coordinate Geometry: It is an analytical geometry that is used for defining the exact position of a point using coordinates.

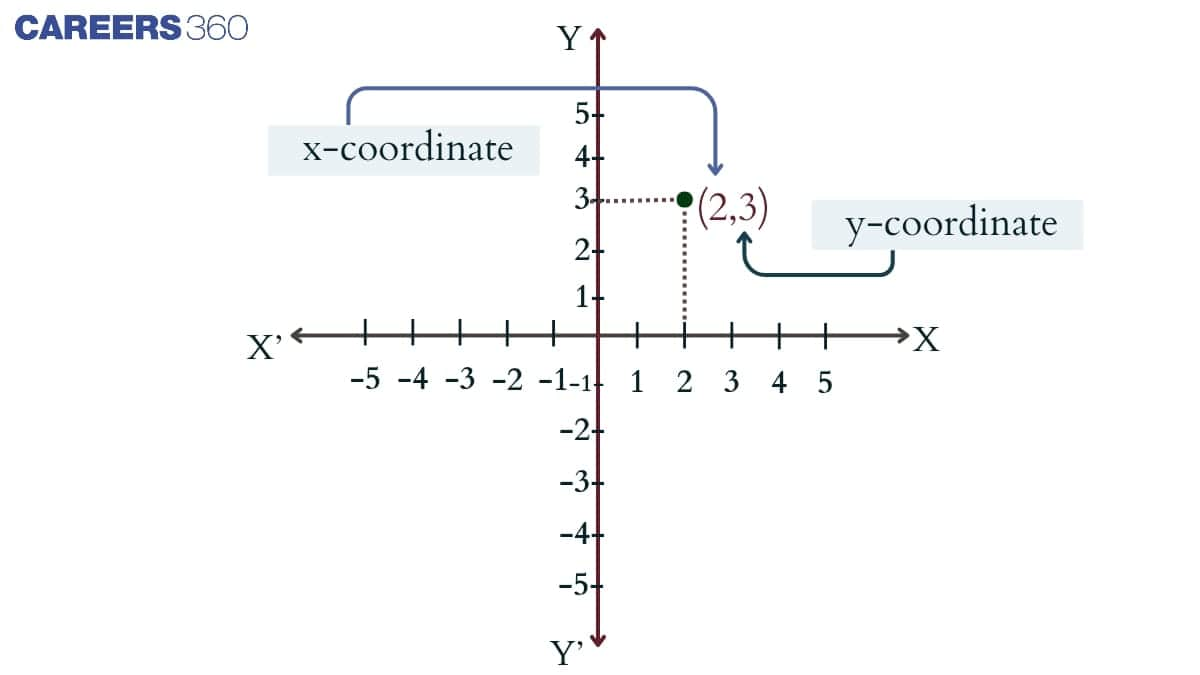
1744428253200

Cartesian System

The Cartesian system is a method of defining the position of a point in a plane. In this method, points are located using two perpendicular lines. In the Cartesian system, the horizontal line is called the X-axis and it is represented by XX', and the vertical line is called Y- axis and it is represented by YY'.

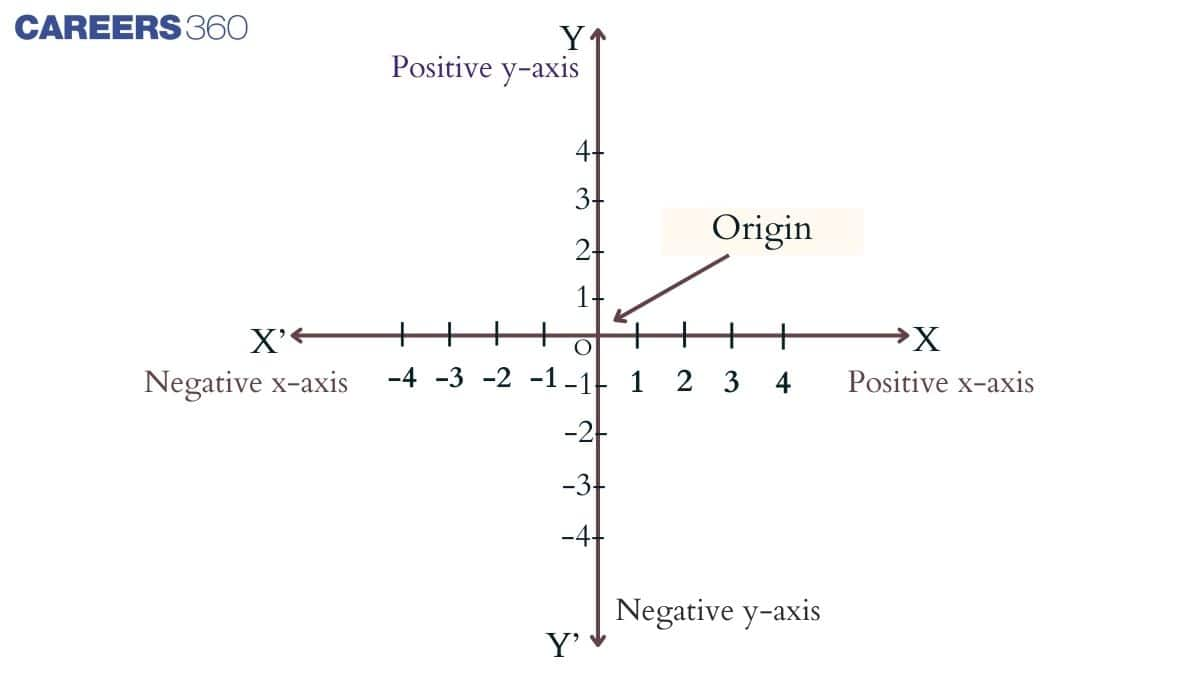
Origin

The place where the two perpendicular lines of the X-axis and the Y-axis intersect is called the origin, and it is denoted by the letter $O$. This origin divides the line into positive and negative directions as OX and OY are called the positive direction, and OX' and OY' are called the negative direction of the graph.

1744428299750

Coordinate Axes and Quadrants

The origin divides the plane into four sections, and these sections are known as quadrants. Quadrants are numbered as I, II, III and IV in an anticlockwise direction starting from the top right section. The plane where these quadrants exist is called the Cartesian plane, coordinate plane or XY plane and the axes on this Cartesian plane are called coordinate axes.

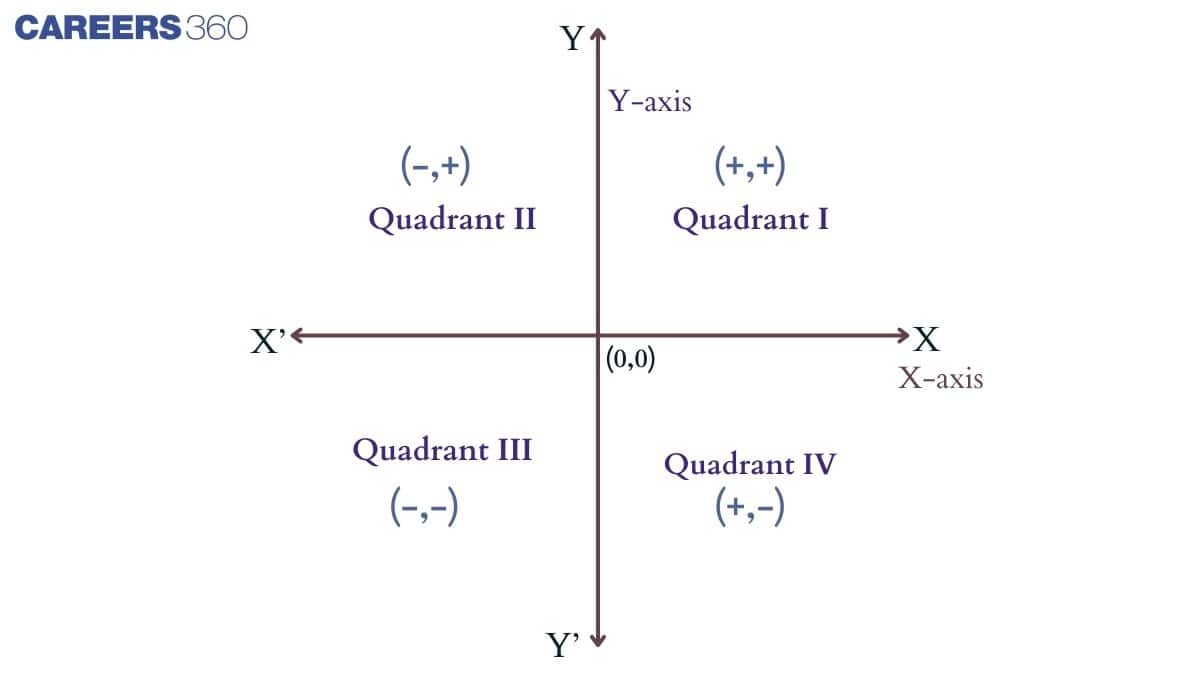
1744428348164

Points in Different Quadrants

The four quadrants in the XY plane are as follows,
Quadrant I: It is represented by (+, +) signs, which means X and Y are both positive.
Example: (2, 7)
Quadrant II: It is represented by (–, +) signs, which means X is negative and Y is positive.
Example: (-3, 4)
Quadrant III: It is represented by (–, –) signs, which means X and Y are both negative.
Example: (-4,-4)
Quadrant IV: It is represented by (+, –) signs, which means X is positive and Y is negative.
Example: (1, -9)

Plotting on a Graph

On the plane, a set of numbers or coordinates is given to define the position of the point in the XY plane, and these coordinate points are represented by an ordered pair of (x, y) where, X or distance from origin to X axis is called abscissa or X-coordinate and the distance from O to Y axis is called the ordinate or Y-coordinate as shown in figure.

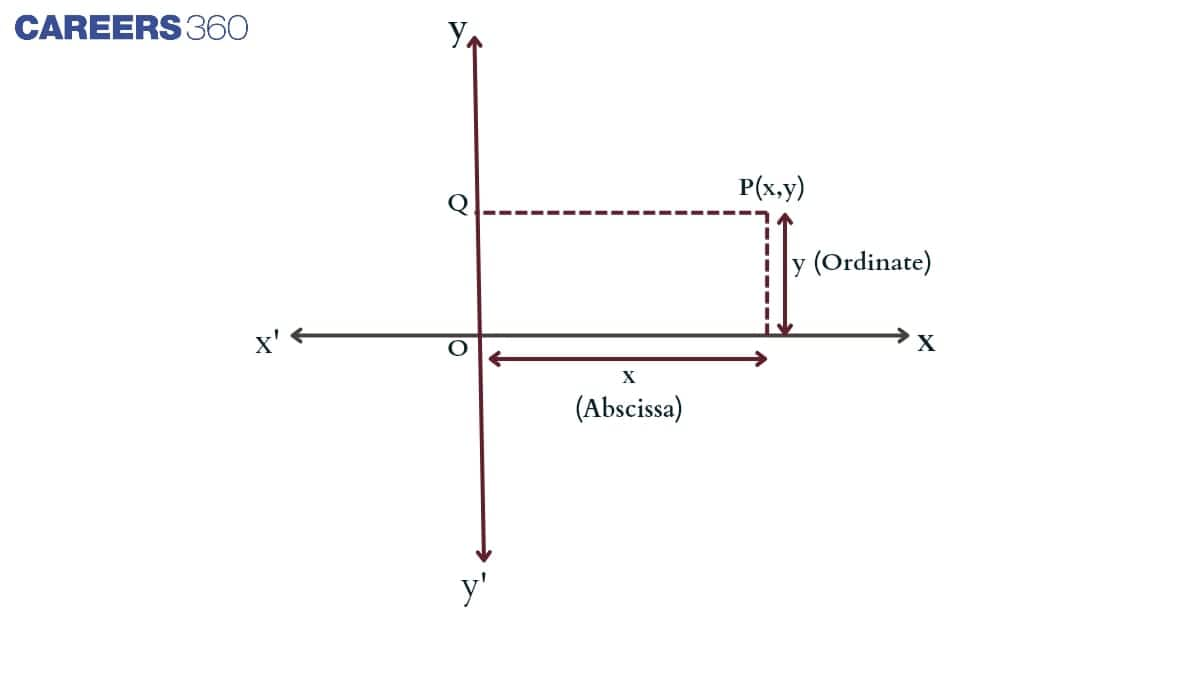
1744428413663

Plotting a Point in the Plane if Its Coordinates Are Given

In the coordinate plan, the X-coordinate implies that the distance from the origin to the X-axis and the Y-coordinate implies that the distance from the origin to the Y-axis. These points can be:
Example: Plot the coordinates (1, 2), (2, -4), (-3, 4) and (-2, -2) in the Cartesian plane.
Here,
(1, 2)→It is 1 unit away from the positive y-axis and 2 units away from the positive x-axis.
(2, -4)→It is 2 units away from the positive y-axis and 4 units away from the negative x-axis.
(-3, 4)→It is 3 units away from the negative y-axis and 4 units away from the positive x-axis.
(-2, -2)→It is 2 units away from the negative y-axis and 2 units away from the negative x-axis.
The plotting of these coordinates is shown in the figure:

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Notes for Class 9 Maths Chapter 1 - Number System

NCERT Notes for Class 9 Maths Chapter 2 - Polynomials

NCERT Notes for Class 9 Maths Chapter 3 - Coordinate Geometry

NCERT Notes for Class 9 Maths Chapter 4 - Linear Equations in Two Variables

NCERT Notes for Class 9 Maths Chapter 5 - Introduction to Euclid’s Geometry

NCERT Notes for Class 9 Maths Chapter 6 - Lines And Angles

NCERT Notes for Class 9 Maths Chapter 7 - Triangles

NCERT Notes for Class 9 Maths Chapter 8 - Quadrilaterals

NCERT Notes for Class 9 Maths Chapter 9 - Circles

NCERT Notes for Class 9 Maths Chapter 10 - Heron's Formula

NCERT Notes for Class 9 Maths Chapter 11 - Surface Areas and Volumes

NCERT Notes for Class 9 Maths Chapter 12 - Statistics

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

Articles

Simultala Awasiya Vidyalaya Admit Card 2025-26; Download the SAV Admit Card for Preliminary Exam

Sep 29, 2025

Simultala Awasiya Vidyalaya Result 2025-26, Check Your Admission Results

Sep 25, 2025

Simultala Awasiya Vidyalaya Answer Key 2025-26, Download SAV Class 6 Answer Sheet Prelims Exam

Sep 25, 2025

RMO Result 2025-26: RMO Provisional Scores (Region Wise) Direct Link @hbcse.tifr.res.in

Sep 25, 2025

Upcoming School Exams

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is