Areas Of Parallelograms And Triangles Class 9th Notes - Free NCERT Class 9 Maths Chapter 9 Notes

Updated on 21 Apr 2022, 02:04 PM IST

Areas Of Parallelograms And Triangles class 9 notes:

The Areas Of Parallelograms And Triangles is the NCERT chapter which deals with The quantity of space inside the edge of a 2D object is referred to as its area. It's a measurement that expresses the size of a two-dimensional figure or shape. Its units are cm², m², hectare, acre, and so on. As a result, the area of a figure is a number in some unit related to the section of the figure that is enclosed. The NCERT Class 9 Maths Chapter 9 Notes covers a brief outline of the chapter Areas Of Parallelograms And Triangles. The main topics covered are Introduction, Same Parallels and on the Same Base, Area of a parallelogram, Area of Triangle, Theorems -Parallelograms on a Common Base and Between the Same Parallels, Triangles with the Same Parallels and a Common Base, Two triangles with the same base and the same area, Between the same parallels, a parallelogram and a triangle in the Areas Of Parallelograms And Triangles class 9 notes with some FAQs.

The basic equations in the chapter are also covered in the class 9 maths chapter 9 notes. All of these topics are covered in Areas Of Parallelograms And Triangles class 9 notes pdf download. In the CBSE class 9 maths chapter 9 notes, the required derivations are not addressed. No, the notes for class 9 maths chapter 9 do not include all of the important derivations. This NCERT note summarises the chapter's important points and equations and can be used to review Areas Of Parallelograms And Triangles.

Also, students can refer,

NCERT Class 9 Maths Chapter 9 Notes

Introduction

A closed geometric figure's area represents the amount of planar surface it covers.

Same Parallels And On The Same Base

If: a) They have a common side, two shapes are said to be on the same base and between the same parallels.

b) The vertices opposite the common side are on the same straight line parallel to the base as the sides parallel to the common base.

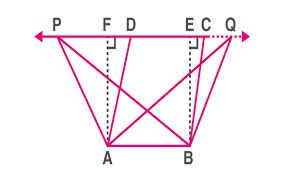
$C:\Users\GOD IS GREAT\Pictures\images.png$

example: Rectangle ABEF, Parallelogram ABCD; and Triangles ABP and ABQ

Area of Parallelogram:

A = b x h

The base is 'b′, and the equivalent altitude is 'h′. (Height).

Area of Triangle:

A = ( 1/2 ) b x h

The base is "b," while the equivalent altitude is "h."

Theorems

Parallelograms On A Common Base And Between The Same Parallels

If two parallelograms have the same base and lie between the same parallels,

a) They are said to be on the same base.

b) The sides parallel to the same side are parallel to each other.

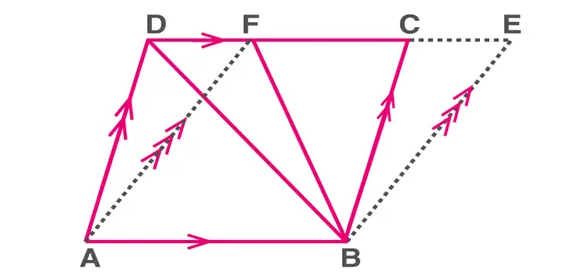
$C:\Users\GOD IS GREAT\Pictures\Screenshots\Screenshot (1340).png$

Theorem: Areas of parallelograms lying on the same base and between the same parallels are equal.

Here, area ( parallelogram ABCD ) = area ( parallelogram ABEF )

Triangles With The Same Parallels And A Common Base

If a) They have a common side, two triangles are said to be on the same base and between the same parallels.
b) The vertices on the opposite side of the common side are parallel to the common side.

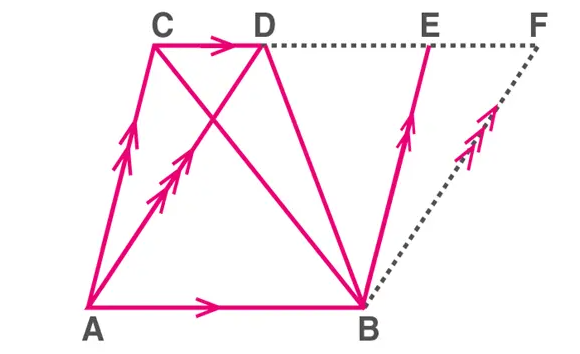
$C:\Users\GOD IS GREAT\Pictures\Screenshots\Screenshot (1339).png$

Theorem: Triangles that share the same or common base and are connected by the same parallels have the same area.

Here, area ( ΔABC ) = area ( ΔABD )

Two Triangles With The Same Base And The Same Area

When two triangles have the same base and area, their associated altitudes are the same.

Between The Same Parallels, A Parallelogram, And A Triangle

A triangle and a parallelogram, are said to be on the same base and between the same parallels.

a) Have the same side
b) The vertices on the opposite side of the common side are parallel to the common side.
Theorem: If a triangle and a parallelogram have the same base and are connected by the same parallels, the triangle's area equals half that of the parallelogram.

Here, area ( ΔABC ) = ( 1/2 ) area of parallelogram ABDE

Significance of NCERT class 9 maths chapter 9 notes

The Areas Of Parallelograms And Triangles in class 9th notes will help you review the chapter and gain a sense of the main points presented.

This NCERT class 9 maths chapter 9 notes can be used to cover the core concepts of the CBSE maths syllabus in class 9 as well as for competitive exams like VITEEE, BITSAT, JEE Main, NEET, and other similar exams.

NCERT solutions of class 9 subject wise

NCERT Class 9 Exemplar Solutions for Other Subjects:

NCERT Class 9 Notes Chapter wise

NCERT Class 9th Math Chapter 1 Notes

NCERT Class 9th Maths Chapter 2 Notes

NCERT Class 9th Maths Chapter 3 Notes

NCERT Class 9th Maths Chapter 4 Notes

NCERT Class 9th Maths Chapter 5 Notes

NCERT Class 9th Maths Chapter 6 Notes

NCERT Class 9th Maths Chapter 7 Notes

NCERT Class 9th Maths Chapter 8 Notes

NCERT Class 9th Maths Chapter 9 Notes

NCERT Class 9th Maths Chapter 10 Notes

NCERT Class 9th Maths Chapter 11 Notes

NCERT Class 9th Maths Chapter 12 Notes

NCERT Class 9th Maths Chapter 13 Notes

NCERT Class 9th Maths Chapter 14 Notes

NCERT Class 9th Maths Chapter 15 Notes

Articles

DU BA LLB Eligibility Criteria 2026 - Age Limit, Qualifications, Marks

Sep 22, 2025

DU LLB Counselling 2026 – Seat Allotment, Documents, Admission Process

Sep 21, 2025

CGPA Calculator - Know How to Calculate CGPA

Sep 19, 2025

SOF IHO Exam 2026 – Dates, Registration, Syllabus & Pattern

Sep 19, 2025

Upcoming School Exams

National Means Cum-Merit Scholarship

Ongoing Dates

NMMS Application Date

25 Jul'25 - 30 Sep'25 (Online)

Uttar Pradesh Board 12th Examination

Ongoing Dates

UP Board 12th Others

10 Aug'25 - 27 Sep'25 (Online)

Mock Test

Exam Pattern

Result

Uttar Pradesh Board 10th examination

Ongoing Dates

UP Board 10th Others

10 Aug'25 - 27 Sep'25 (Online)

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is