Statistics Class 9th Notes - Free NCERT Class 9 Maths Chapter 14 Notes

Updated on 21 Apr 2025, 03:19 PM IST

Statistics is an applied mathematics that deals with the collection, interpretation and analysis of data. Statistics is used to compute, manipulate or organise data. Many types of manipulation operations can be performed on large data sets. With the help of statistics, different types of data can be compared in a single frame. It is used to convert the raw data into useful information. There are many applications of statistics, like weather forecasting, probability, geology, psychology, and medical studies etc. Some real-life applications are in business, like marketing for comparing market trends.

This Story also Contains

NCERT Class 9 Maths Chapter 12 Statistics: Notes
Graphical Representation of Data
Class 9 Chapter Wise Notes
NCERT Solutions for Class 9
NCERT Exemplar Solutions for Class 9
NCERT Books and Syllabus

Statistics

In these notes, students learn the definition of statistics and its basic concepts, such as data, frequency, types of data, class intervals and their types, and related formulae, such as mean, mode, or median. The CBSE Class 9 chapter includes questions and examples for the given topics as required. In these NCERT class 9th maths notes, all the chapters, topics, and subtopics are covered according to the latest syllabus. Students from different standards can download the NCERT notes according to their requirements.

NCERT Class 9 Maths Chapter 12 Statistics: Notes

Statistics

A branch of mathematics concerned with data collection, analysis, interpretation and presentation is known as statistics.

Data

Any numerical or non-numerical figures, facts or other information that is collected for a particular purpose is called data.

Frequency

The number of occurrences of a particular datum is called the frequency.

Ungrouped Data

When the observation is not organised in groups, then this type of data is called ungrouped data.

Grouped Data

When the observations are organised in groups, this is called grouped data.

Class Interval

The size of the data on which the class is divided is called the class interval.

Class width = upper class limit – lower class limit

Regular and Irregular Class Interval

When the class interval is of the same size, it is called a regular class interval.
Example: 0 - 10, 10 - 20, 20 - 30, 30 - 40

When the class interval is of a different size, it is called an irregular class interval.
Example: 0 - 10, 10 - 35, 35 - 45, 45 - 60

Frequency Table

It shows the occurrence of a particular variable in a tabular form.

Sorting

Arranging data in a particular order (ascending or descending order) is called sorting data.

Ungrouped Frequency Table

A frequency table in which data is not arranged in any particular order, then is called an ungrouped frequency table.

Grouped Frequency Table

A frequency table in which data is arranged in any particular order, either in ascending or descending order then is called a grouped frequency table.

Graphical Representation of Data

Some of the graphical representations of data are as follows.

Bar Graphs

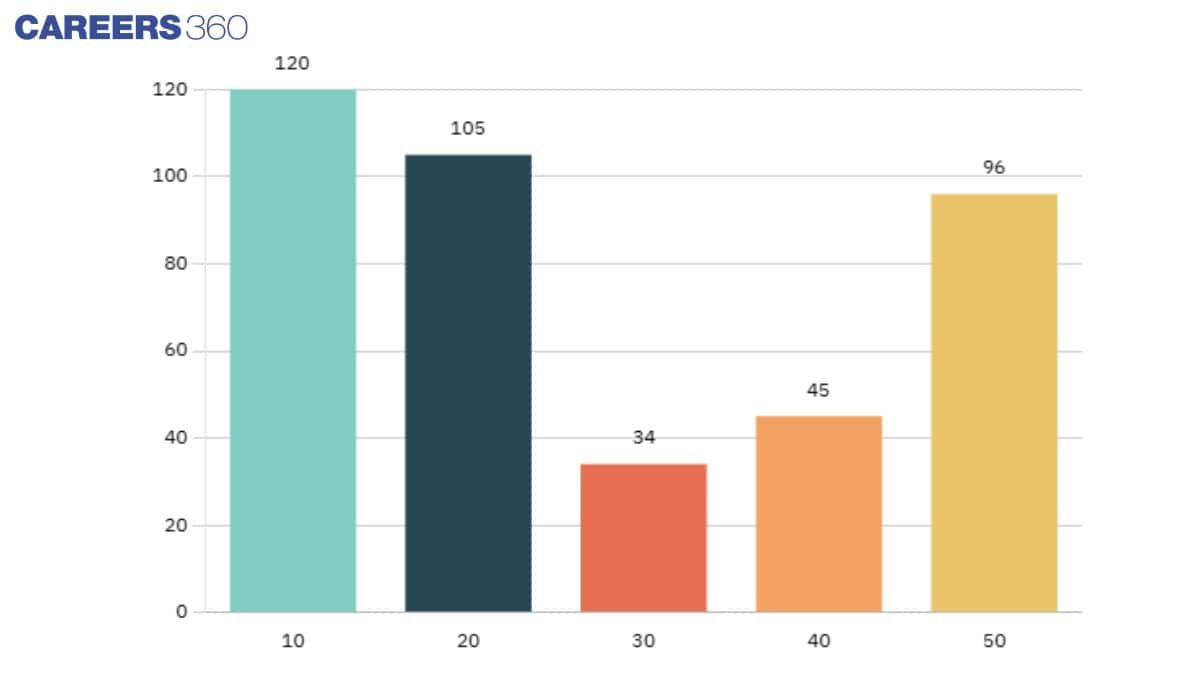
Bar graphs represent data using bars of equal width and space between them on the axis. The frequency of data is represented through the height of the bar. Bar graphs are used for discrete data intervals.
For example:

Number of People	Weight (Frequency)
10	120
20	105
30	34
40	45
50	96
Total	400

The representation of these data in a bar graph is as follows.

1744474513639

Histograms

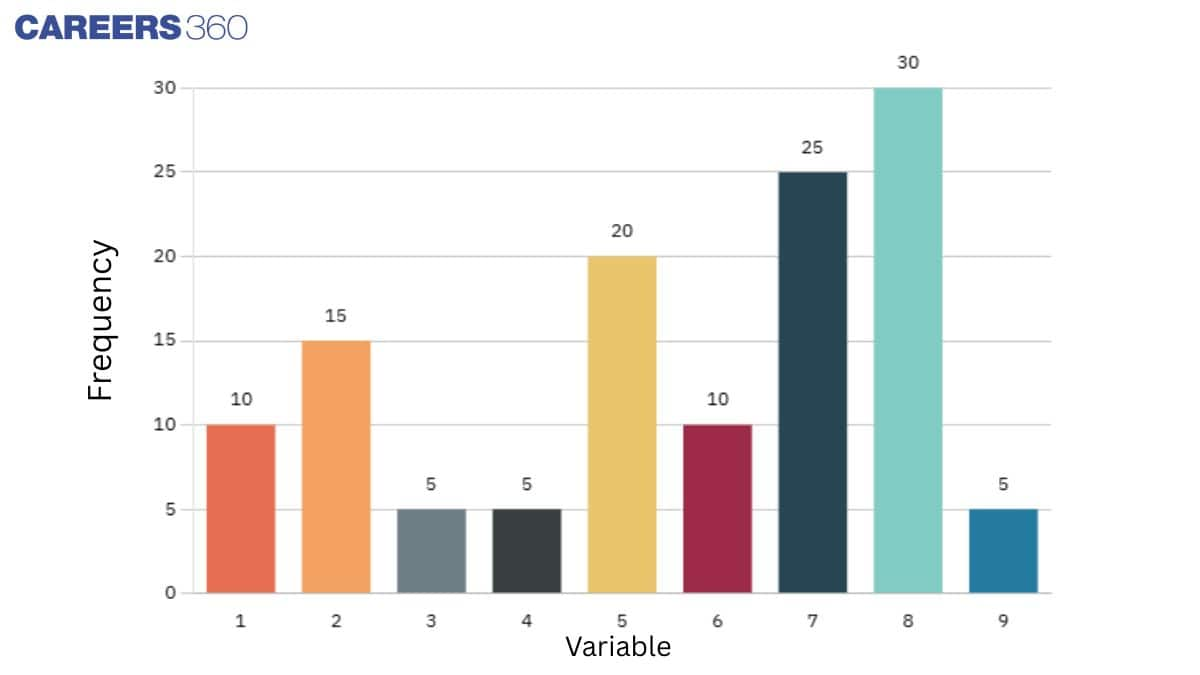
Similar to the bar graph, histograms are also used for the graphical representation of data, but this is used for continuous data intervals. In this graph, the area of the rectangle or frequency represented by the height of the graph and width is called the class intervals.

1744474513956

Frequency Polygon

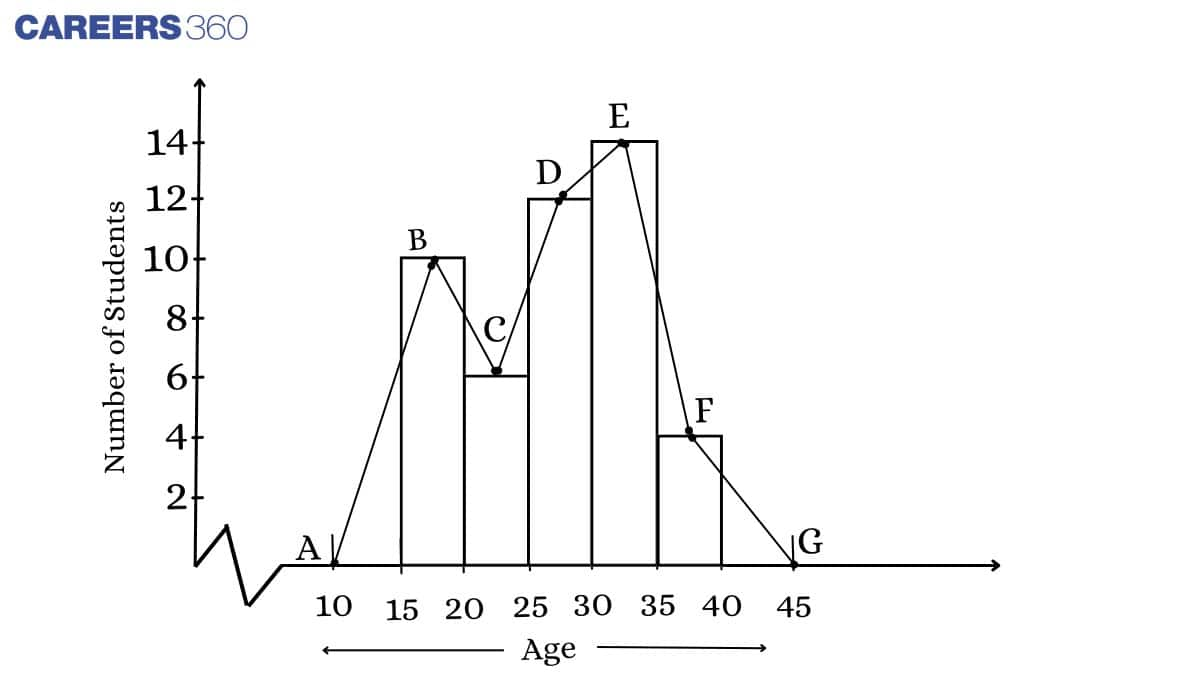
When the midpoints of each rectangle are joined by using line segments in the histogram, this is called the frequency polygon. It can be drawn without a histogram.

1744474514531

Midpoint of the Class Interval

The class mark or the midpoint of the circle can be calculated as:

Class mark = $\frac{(Upper limit + Lower limit)}{2}$

A frequency polygon can be drawn using the given class mark.

Example: In a company, employees of different departments work for different numbers of months and the tabular data is shown below. Draw the histogram for the table shown below.

Number of Employees	Number of Months
50 - 100	7
100 -150	10
150 - 200	20
200 - 250	6
Total	43

Class mark = $\frac{(Upper limit + Lower limit)}{2}$

Class mark = $\frac{(100 + 50)}{2}$ = 75

Similarly, determine the class mark for all values.

Number of Employees	Class Marks	Number of Months
50 - 100	75	8
100 -150	125	10
150 - 200	175	20
200 - 250	225	8
Total		45

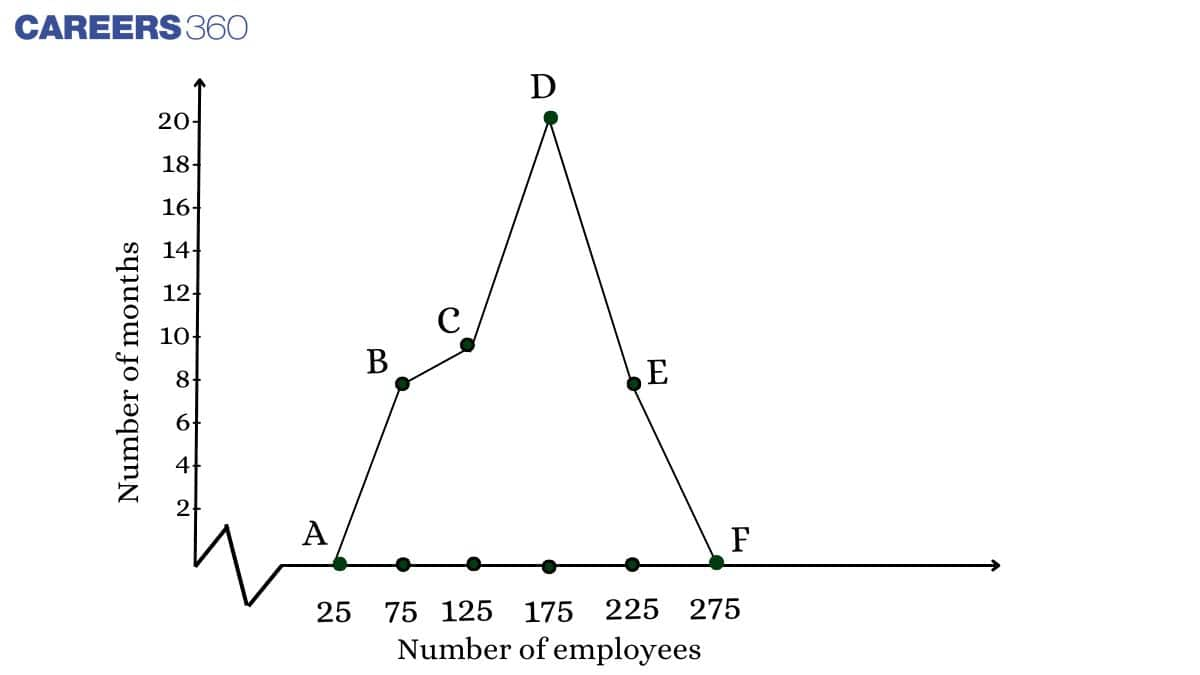
1744474514788

The histogram for the given tabular data is shown below; in this graph, ABCDEF is called the frequency polygon.

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Notes for Class 9 Maths Chapter 1 - Number System

NCERT Notes for Class 9 Maths Chapter 2 - Polynomials

NCERT Notes for Class 9 Maths Chapter 3 - Coordinate Geometry

NCERT Notes for Class 9 Maths Chapter 4 - Linear Equations in Two Variables

NCERT Notes for Class 9 Maths Chapter 5 - Introduction to Euclid’s Geometry

NCERT Notes for Class 9 Maths Chapter 6 - Lines And Angles

NCERT Notes for Class 9 Maths Chapter 7 - Triangles

NCERT Notes for Class 9 Maths Chapter 8 - Quadrilaterals

NCERT Notes for Class 9 Maths Chapter 9 - Circles

NCERT Notes for Class 9 Maths Chapter 10 - Heron's Formula

NCERT Notes for Class 9 Maths Chapter 11 - Surface Areas and Volumes

NCERT Notes for Class 9 Maths Chapter 12 - Statistics

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

Articles

DU LLB Counselling 2026 – Seat Allotment, Documents, Admission Process

Sep 21, 2025

CGPA Calculator - Know How to Calculate CGPA

Sep 19, 2025

SOF IHO Exam 2026 – Dates, Registration, Syllabus & Pattern

Sep 19, 2025

NRTS Answer Key 2025 - Check National Rural Talent Scholarship Exam Result Solution Key Here

Sep 19, 2025

Upcoming School Exams

National Means Cum-Merit Scholarship

Ongoing Dates

NMMS Application Date

25 Jul'25 - 30 Sep'25 (Online)

Assam High School Leaving Certificate Examination

Ongoing Dates

Assam HSLC Application Date

1 Sep'25 - 4 Oct'25 (Online)

Maharashtra Higher Secondary School Certificate Examination

Ongoing Dates

Maharashtra HSC Board Application Date

8 Sep'25 - 30 Sep'25 (Online)

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is