NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

A polynomial is an algebraic expression that is made up of variables and constants. In polynomial expressions, variables are also known as indeterminants and coefficients. A polynomial can have a single or multiple variables. A polynomial expression with more than one variable comprises the arithmetic operations like addition, subtraction and multiplication. These arithmetic operations define the relationship between variables and constants. Polynomials have many applications in different fields like science, engineering, and economics as a fundamental tool for analysing and solving problems. Polynomials are also used in medicine, as well as in the prediction and optimisation of complex issues.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

1. NCERT Class 9 Maths Chapter 2 Polynomials: Notes
2. Factorisation of Polynomials:
3. Algebraic Identities
4. Class 9 Chapter Wise Notes
5. NCERT Solutions for Class 9
6. NCERT Exemplar Solutions for Class 9
7. NCERT Books and Syllabus

These notes cover basic definitions of polynomials, types of polynomials, algebraic expressions, the factor theorem, and the remainder theorem. It also includes all the required formulae, topics and subtopics related to polynomials. In addition, it also includes algebraic identities. CBSE Class 9 chapter Polynomials also includes the geometrical representation of the zeroes of polynomials. NCERT class 9th maths notes help the students to understand the concepts of each chapter with the help of definitions, formulas, and examples, and these NCERT notes are designed according to the latest syllabus of NCERT.

NCERT Class 9 Maths Chapter 2 Polynomials: Notes

Polynomials: Polynomials are an algebraic expression that has one or more variables with non-negative exponents. A polynomial can be represented by $P(x)$ where $P$ is called a polynomial in $x$ and the exponent of $x$ is called the highest degree of $x$. As shown in the figure below.

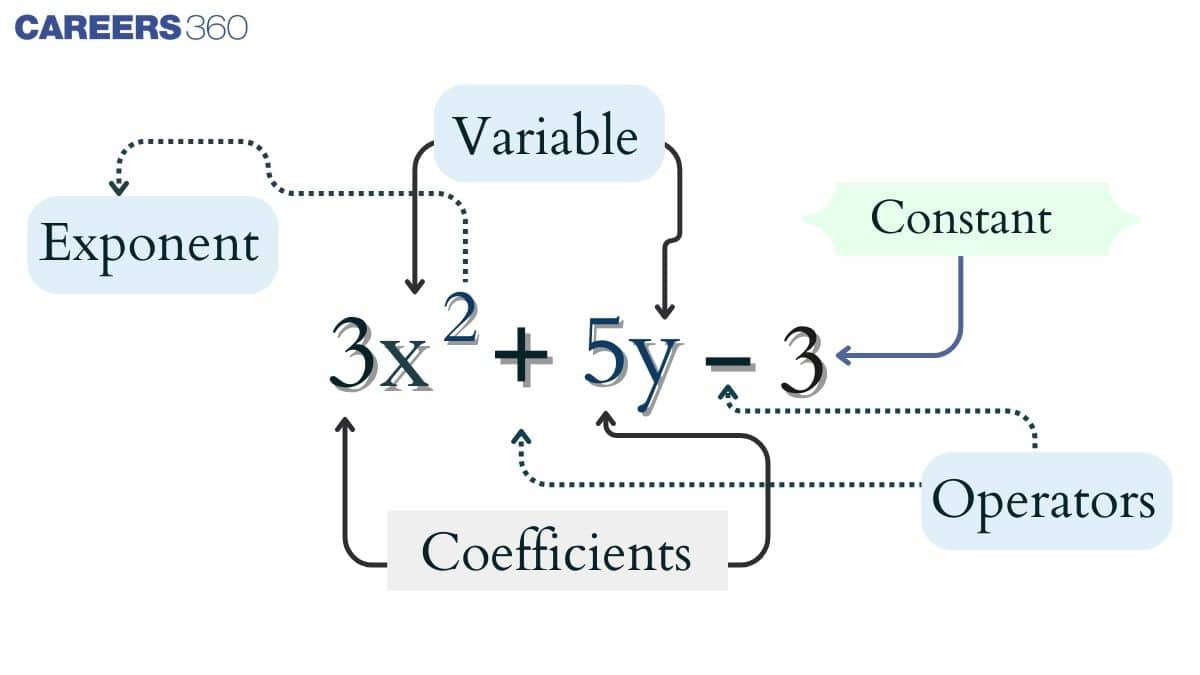
Example: 2x + 1, 3xy, 3x3 + 2x2 + x + 1, x + y + z etc.

Terms:

An expression that is a part of the polynomial expression is called a term.

Example: 4x2 + 2x + 2
Where 4x2, 2x and 2 are the terms of a polynomial expression.

Coefficient

A factor that multiples a variable or a term is called a coefficient. A coefficient can be a whole number, a fraction or a decimal, and these numbers can be negative or positive.

Types of Polynomials:

Based on the degrees and terms that a polynomials have, polynomials can be classified into two categories:
1. Number of terms
2. Degree of polynomials

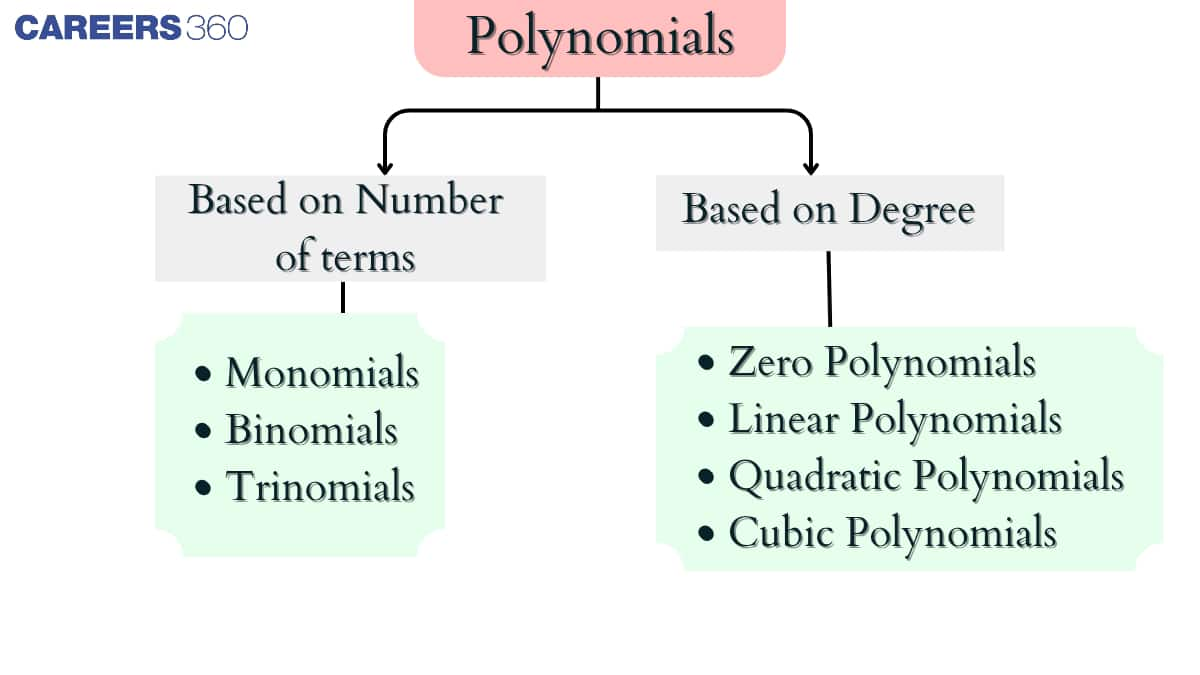
Based On Number Of Terms:

A polynomial expression can have one or more terms, and according to the number of terms, polynomials are as follows -
1. A polynomial with only one term is called a monomial.
Example: $4x$, $7pq$, $9p$2

2. A polynomial with only two unlike terms is called a binomial.
Example: $4x + 1$, $7y$2 + $3$

3. A polynomial with only three unlike terms is called a trinomial.
Example: $4y$2 + $2y$ - $2$

Based On Degree Of Polynomials:

1. A polynomial with 0 as a degree is called a zero or constant polynomial.
Example: $2x$0, $5y$0

2. A polynomial with 1 as a degree is called a linear polynomial.
Example: $3x$ + $1$, $4y$ + $5$

3. A polynomial with 2 as a degree is called a quadratic polynomial.
Example: $5x$2 + $3x$ + $1$

4. A polynomial that has 3 as a degree is called a cubic polynomial.
Example: $7x$3 + $5x$ - $2$

Polynomials in One Variable:

A polynomial expression that has one type of variable in the entire expression is known as a polynomial in one variable.
Example: 8x2 + 4x + 2, 5y + 2, 6z.

Zeros of A Polynomial:

The value of the variable that makes polynomials equal to zero is called the zeros of a polynomial.

Example: For the polynomial $p(y)$ = $x$2 - $9$, the zeros are $x = 3$ and $x = -3$, because $p(3)$ = $3$2 - $9$ = $0$ and $p(-3) = (-3)² - 9 = 0$

Finding Zeros of Polynomials for Linear Equations:

The standard form of a linear equation is P(x) = ax + b, and for this equation, the formula for finding the zeros is as follows:
Zero of Polynomial (x) = $\frac{-Constant}{\text{ Coefficent of x}}$

Example: Find the zero of a polynomial P(x) = 2y - 8.
Here,
Constant = 8
Coefficient = 2

Zero of Polynomial (y) = $\frac{-Constant}{\text{ Coefficent of y}}$

Zero of Polynomial (y) = $\frac{-8}{2}$

Zero of Polynomial (y) = $-4$

Finding Zeros of Polynomials for Quadratic Equations:

The standard form of a quadratic equation is ax2 + bx + c = 0, where a, b and c are constants. Therefore, the formula for finding zeros of quadratic equations is:

$X$ = $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Example: Find the zeros of a polynomial of the quadratic equation 5x2 + 4x + 1 = 0.
After comparing the question equation with the standard quadratic equation ax2 + bx + c = 0, we get,
a = 5
b = 4
c = 1
And,

$X$ = $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

After putting the values in the formula, we get,

$X$ = $\frac{-4 \pm \sqrt{4^2 - 4 x 5 x 1}}{2 x 5}$

$X$ = $\frac{-4 \pm \sqrt{16 - 20}}{10}$

$X$ = $\frac{-4 \pm \sqrt{-4}}{10}$

$X$ = $\frac{-4 \pm {-2}}{10}$

Therefore, $x$ = $\frac{-3}{5}$ and $x$ = $\frac{-1}{5}$

Relationship Between Zeros And Coefficients Of a Polynomial:

For quadratic Polynomials, the standard quadratic equation is:
ax2 + bx + c and let α and β be the roots of the standard quadratic equation, then,

Sum of the zeroes (α + β) = $\frac{-b}{a}$ or $\frac{\text{-Coeffiecient of x}}{\text{Coeffiecinet of x}^2}$

Product of the zeroes (αβ) = $\frac{c}{a}$ or $\frac{\text{Constant term}}{\text{Coefficient of x}^2}$

Example: x2 + 7x + 10
After comparing the question equation with the standard quadratic equation ax2 + bx + c = 0, we get,
b = 7
a = 1
c = 10

Sum of the zeroes (α + β) = $\frac{-7}{1}$

Product of the zeroes (αβ) = $\frac{10}{1}$

For Cubic Polynomials: Let α, β and γ be the roots of a cubic polynomial ax3 + bx2 + cx + d, then

α + β + γ = $\frac{-b}{a}$

αβ + βγ + γα = $\frac{c}{a}$

αβγ = $\frac{-d}{a}$

Example: Find zeros for the polynomial equation P(x) = 3x3 + 2x2 + x + 2

After comparing the equation with standard polynomial equation ax3 + bx2 + cx + d we get,
a = 3
b = 2
c = 1
d = 2

α + β + γ = $\frac{-b}{a}$

αβ + βγ + γα = $\frac{c}{a}$

αβγ = $\frac{-d}{a}$

After putting in the values, we get,

α + β + γ = $\frac{-2}{3}$

αβ + βγ + γα = $\frac{1}{3}$

αβγ = $\frac{-2}{3}$

Remainder Theorem:

It is a fundamental method that is used to determine the remainder of the polynomials when a polynomial is divided by a linear expression. If P(x) is a polynomial with degree greater than or equal to 1 and if the polynomial is divided by (x-a), then P(a) is called the remainder. Here, (x-a) is called the divisor of the polynomial P(a) is equal to 0. This is applied in factorizing polynomials.

The general formula is as follows:

${P(x)}$ = $(x - a) Q(x) + P(a)$

Where,
P(x) = Polynomial equation
Q(x) = Quotient
P(a) = Remainder
(x - a) = Divisor

Example: If P(x) is 6x2 + 5x + 1 is divided by x - 2 and the quotient is 6x + 17, then the remainder will be 35.
Here, x - 2 is a divisor, and we know that,
x - a = 0,
Therefore, x - 2 = 0
x = 2
By placing the values in the P(x), we get,
= 6(2)2 + 5 x 2 + 1
= 24 + 10 + 1
= 35

Factor Theorem:

When the polynomials are completely divisible, the factor theorems are used. It is used for factoring polynomials or for finding the roots.

Proof Using Remainder Theorem:

Let P(x) be a polynomial which is divided by (x - a), then P(a) = 0.
According to the remainder theorem,
P(x) = (x - a) × Q(x) + P(a)
Since, P(a) = 0, then
P(x) = (x - a) × Q(x) + P(a)
It is proved that (x - a ) is a factor of the polynomial P(x).

Factorisation of Polynomials:

The process of defining the polynomials as the product of two or more terms is known as the factorisation of polynomials.

Example: Find the roots of the polynomial P(x) = 6x2 + 17x + 5 using the factorisation method.

P(x) = 6x2 + 17x + 5

⇒ 6x2 + 15x + 2x + 5 = 0

⇒ 3x(2x + 5) + 1(2x + 5) = 0

⇒ (2x + 5), (3x + 5)

x = $\frac{-5}{3}$, $\frac{-5}{2}$,

Algebraic Identities

In polynomials, some algebraic identities are given that are valid for certain values. Algebraic identities are equations and identities are as follows:

1. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
   
   
2. (x + y)3 = x3 + y3 + 3xy(x + y)
   
   
3. (x – y)3 = x3 – y3 – 3xy(x – y)
   
   
4. x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Syllabus for Class 9
• NCERT Books for Class 9