Surface Areas And Volumes Class 9th Notes - Free NCERT Class 9 Maths Chapter 13 Notes - Download PDF

The world contains numerous three-dimensional objects, which include boxes together with cans and balls, as well as pipes. The objects possess two features: areas to measure and inner space to fill. This chapter offers methods to determine the exterior surface area and internal volume measurement of cubic shapes, including cuboids, cubes, and cylinders solve practical issues, such as wall painting requirements and tank water capacity determination. The information provides valuable tools for examinations and serves important functions in everyday life and architectural engineering design professions. Students should use the excellent NCERT class 9th maths notes to establish foundational mathematical concepts and efficiently review key concepts of the various subjects, cones, spheres and also the hemispherical geometry.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

1. NCERT Notes Class 9 Maths Chapter 13 Surface Areas and Volumes
2. Surface Area and Volume of a Cube:
3. Surface Area and Volume of a Cuboid:
4. Surface Area and Volume of a Right Circular Cylinder:
5. Surface Area and Volume of a Right Circular Cone:
6. Surface Area and Volume of a Sphere:
7. Surface Area and Volume of a Hemisphere:
8. Class 9 Chapter Wise Notes
9. NCERT Solutions for Class 9
10. NCERT Exemplar Solutions for Class 9
11. NCERT Books and Syllabus

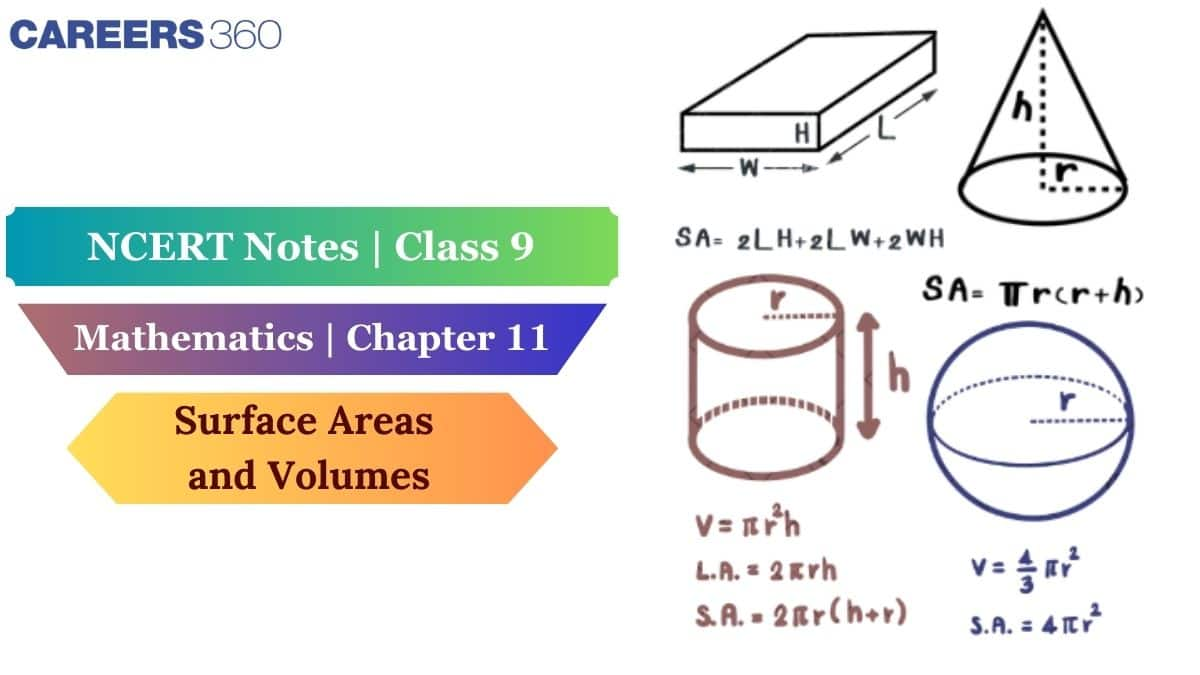
The chapter provides basic formulas which solve practical issues that include wall painting requirements and tank water capacity determination. The information provides valuable tools for examinations and serves important functions across everyday life situations and architectural engineering design professions. Students should use the excellent NCERT class 9th maths notes to establish foundational mathematical concepts. And, efficiently utilise the NCERT Notes to review key concepts of the various subjects.

NCERT Notes Class 9 Maths Chapter 13 Surface Areas and Volumes

Surface Area: The entire space which the external surface of an object takes up is known as the surface area of that object.

(Measured in square units, e.g., cm², m²)

Volume: The measurement of the space occupied by an object is referred to as volume.

(Measured in cubic units, e.g., cm³, m³)

Surface Area and Volume of a Cube:

A cube is a cuboid with the same length, width, and height. Six surfaces, twelve edges, eight corners, and four diagonals make up a cube. Example: a dice.

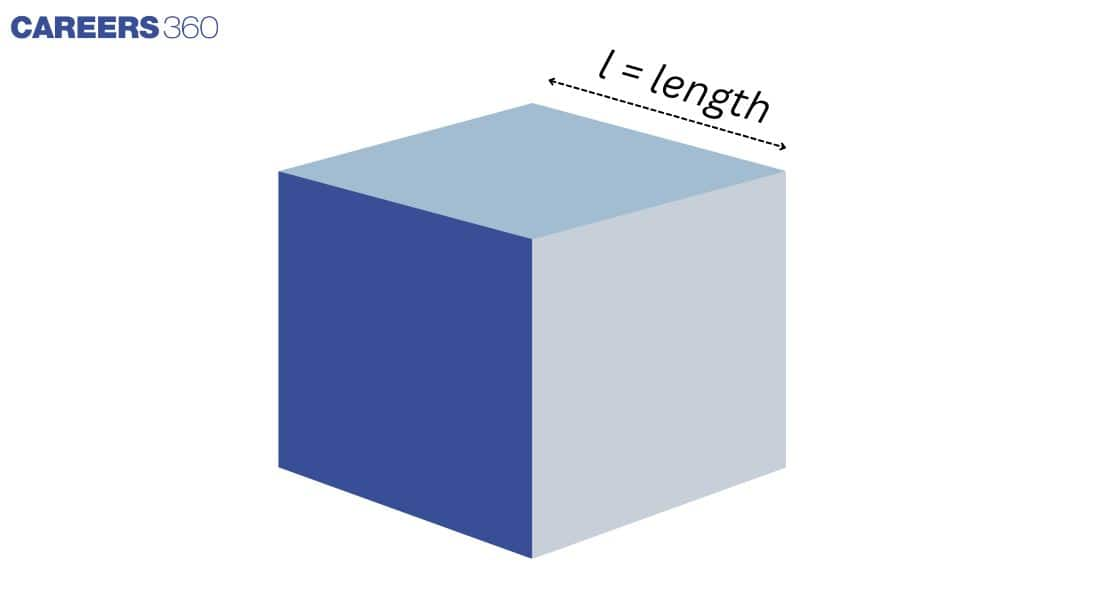
Total Surface Area: 6 × (side)²

Lateral Surface Area: 4 × (side)²

Volume: (side)³

Example:

If side = 3 cm, then Volume = (side)³ = 3³ = 27 cm³

Surface Area and Volume of a Cuboid:

A cuboid is a figure that is surrounded by six rectangular surfaces, with opposite surfaces equal and parallel. In a Cuboid, 12 edges and 8 corners are there. The vertex of a cuboid is each of its four corners. The diagonal of a cuboid is the line segment connecting the opposite vertices. In a cuboid, there are four diagonals. Example: a brick or a matchbox.

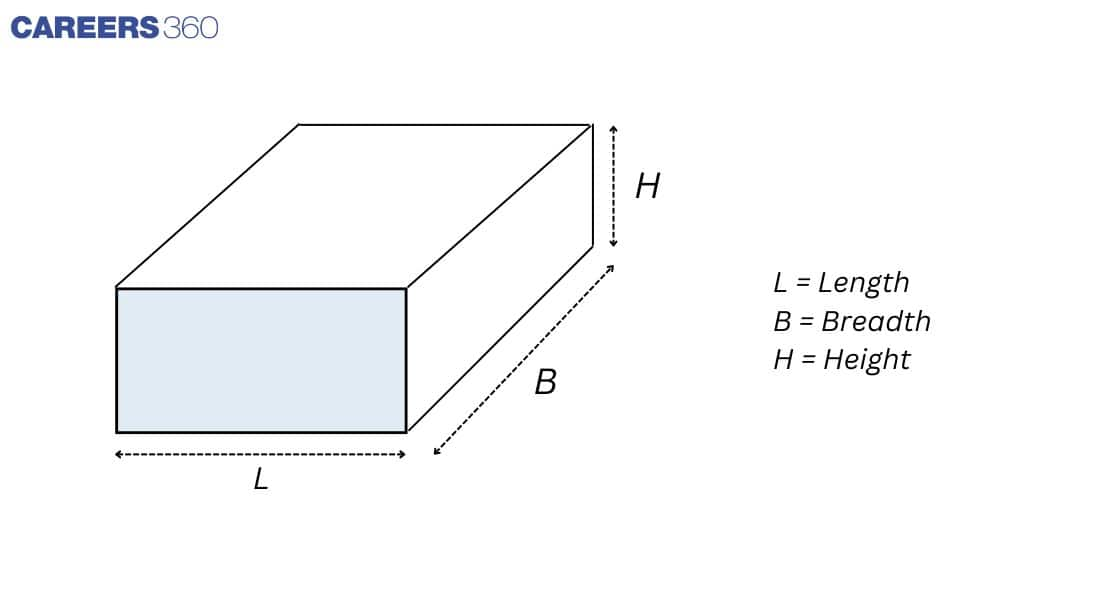
L = Length, B = Breadth and H = Height

Total Surface Area: 2 × (lb + bh + hl)

Lateral Surface Area: 2 × (l + b) × h

Volume: l × b × h

Example:

If l = 5 cm, b = 4 cm, h = 3 cm, then Volume = l × b × h = 5 × 4 × 3 = 60 cm³

Surface Area and Volume of a Right Circular Cylinder:

A solid generated by the revolution of a rectangle around one of its sides is known as a right circular cylinder. It is a three-dimensional shape having two congruent and parallel sides. Thus, two circular and one lateral face, when combined, form a cylinder as shown in the figure. Example: a cold drink can or a water tank.

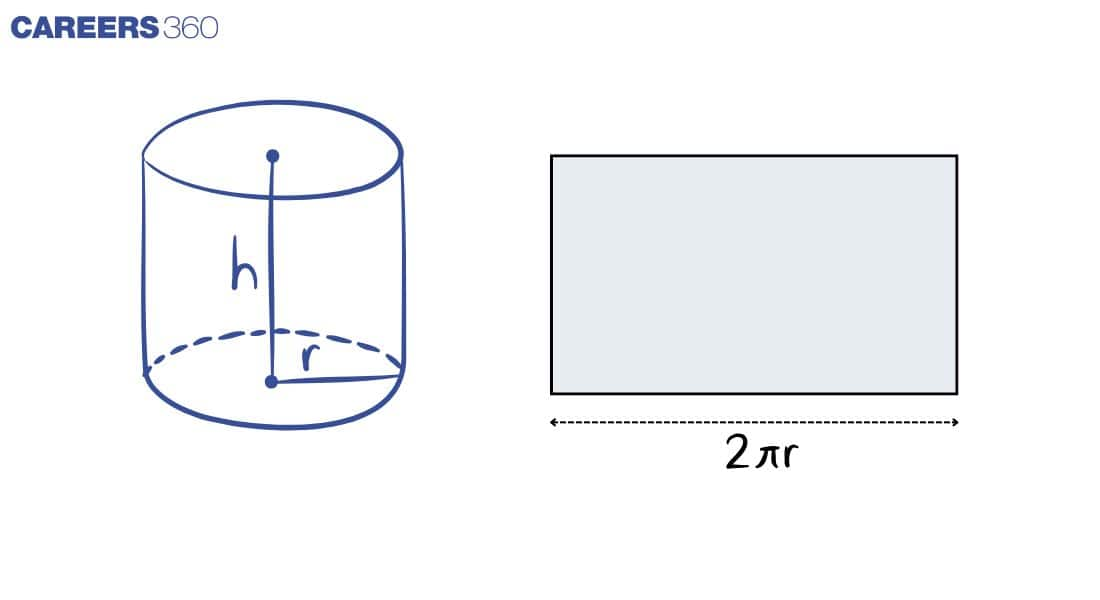
R = Radius and H = Height

Total Surface Area: 2πr(h + r)

Curved Surface Area: 2πrh

Volume: πr²h

Example:

If r = 7 cm, h = 14 cm, π = $\frac{22}{7}$, then Curved surface area = 2πrh = 2 × $\frac{22}{7}$ × 7 × 14 = 616 cm²

Surface Area and Volume of a Right Circular Cone:

A right circular cone is a solid formed when a right triangle is rotated around one of its sides (other than the hypotenuse). Thus, it contains a circular base and a curved surface that gradually decreases to a single point called the vertex. Example: an ice cream cone.

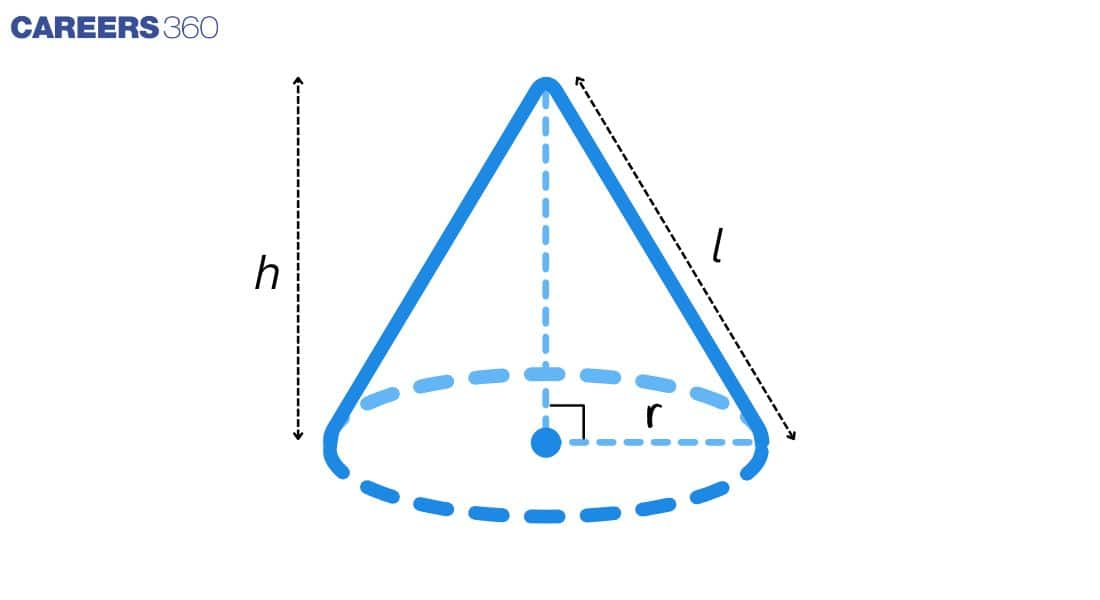
R = Radius, L = Slant Height and H = Height

Total Surface Area: Curved surface area + Base area

⇒ πrl + πr²

Curved Surface Area: πrl

Volume: $\frac{1}{3}$ × πr²h

Example:

If r = 7 cm, h = 12 cm, π = $\frac{22}{7}$,

then Volume = $\frac{1}{3}$ × πr²h

= $\frac{1}{3}$ × $\frac{22}{7}$ × 7 × 7 × 12 = 616 cm³

Surface Area and Volume of a Sphere:

A sphere is the spatial area of a solid that touches a curved surface by which every point maintains an equal distance to its fixed centre. The centre point of the sphere serves as its fixed position. A sphere possesses a radius that represents the straight distance from its centre point to the surface. Example: ball

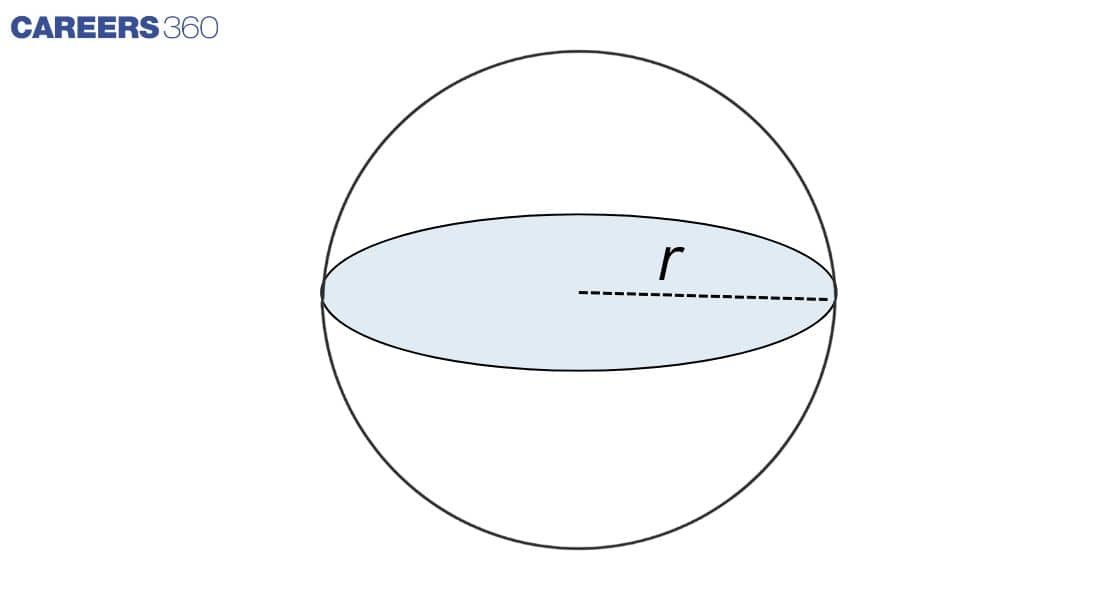
R = Radius

Surface Area: 4πr²

Volume: $\frac{4}{3}$ × πr³

Example:

If r = 21 cm, π = $\frac{22}{7}$,

then Volume = $\frac{4}{3}$ × πr³

= $\frac{4}{3}$ × $\frac{22}{7}$ × 21 × 21 × 21 = 38808 cm³

Surface Area and Volume of a Hemisphere:

A plane which passes through the sphere's centre produces equal halves which correspond to each other as two separate hemispheres. Each divided part of the sphere is named a hemisphere. Example: a dome

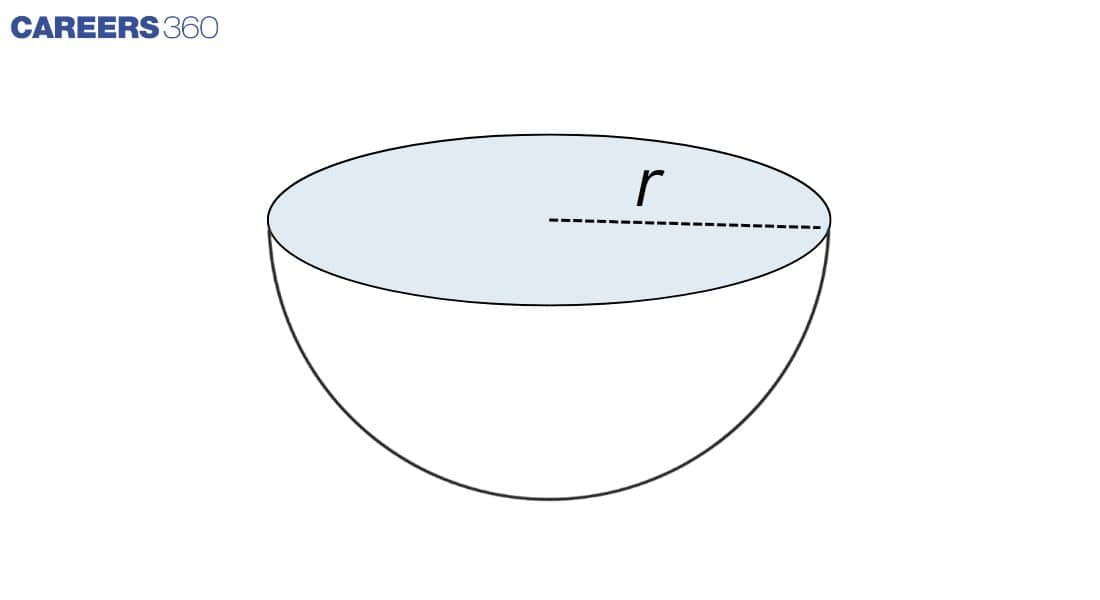
R = Radius

Total Surface Area: 3πr²

Curved Surface Area (CSA) = 2πr²

Volume: $\frac{2}{3}$ × πr³

Example:

If r = 21 cm, π = $\frac{22}{7}$,

then Volume = $\frac{2}{3}$ × πr³

= $\frac{2}{3}$ × $\frac{22}{7}$ × 21 × 21 × 21 = 19404 cm³

Class 9 Chapter Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 10 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Syllabus for Class 9
• NCERT Books for Class 9