NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.1 - Heron's Formula

Q1 A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a ’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Answer:

Given: Perimeter of the equilateral triangle is 180 cm.

Therefore each side of triangle is:

a = 1803 = 60 cm

Now, Calculate the semi-perimeter:

s = Perimeter2=1802 = 90 cm

Use Heron’s Formula to find the area, that is:

Area = s(s−a)(s−b)(s−c)

Thus,

Area = 90(90−60)(90−60)(90−60)=90×30×30×30

Area = 90×27000=2430000=9003 cm2.

Q2 The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of Rs. 5000 per m ² per year. A company hired one of its walls for 3 months. How much rent did it pay?

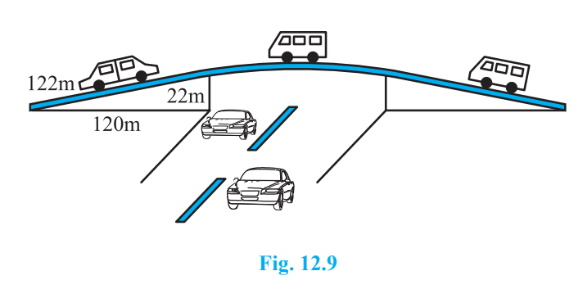
Answer:

From the figure,

Let, the sides of the triangle be:

a = 122m, b = 120m and c = 22m

Therefore, the semi-perimeter, s, will be

s=a+b+c2=122+120+222=2642=132m

Thus, Area ( using Heron’s formula ):

A=s(s−a)(s−b)(s−c)

=132(132−122)(132−120)(132−22) m2

=132(10)(12)(110) m2

=(12×11)(10)(12)(11×10) m2=1320 m2

Given, the rent for 1 year (i.e., 12 months) per square meter is Rs. 5000.

Thus, rent for 3 months per square meter will be:

Rs. 5000×312

Therefore, for 3 months for 1320 m²:

Rs. 5000×312×1320=Rs. 16,50,000.

Q3 There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

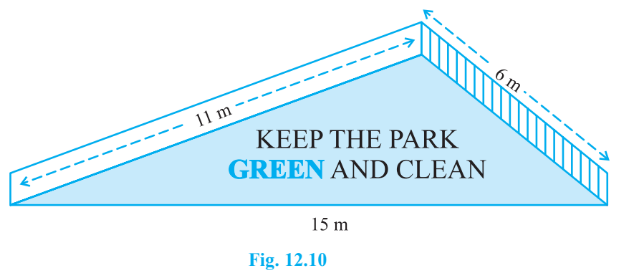Answer:

We are given the sides of the triangle, that are:

a = 15 m, b = 11m and c = 6m

So, the semi-perimeter of the triangle will be:

s=a+b+c2=15+11+62=322=16m

Therefore, area painted in colour is:

A=s(s−a)(s−b)(s−c)

=16(16−15)(16−11)(16−6)

=16(1)(5)(10)

=(4×4)(1)(5)(5×2)

=4×52=202 m2

Q4 Find the area of a triangle two sides of which are 18cm and 10cm and the perimeter is 42cm.

Answer:

Given the perimeter of the triangle is 42cm and the lengths of two sides, a = 18 cm and b = 10 cm.

So, a+b+c=42cm

Or, c=42−18−10=14cm

Thus, the semi-perimeter of the triangle will be:

s=Perimeter2=42cm2=21cm

Therefore, the area given by the Heron's Formula will be,

A=s(s−a)(s−b)(s−c)

=21(21−18)(21−10)(21−14)

=(7×3)(3)(11)(7)

=2111 cm2

Q5 Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.

Answer:

Given the sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm.

Let, the length of one side of the triangle to be a=12x

Then, the remaining two sides be b=17x and c=25x.

Thus, by the given perimeter,

Perimeter = a + b + c = 12x + 17x + 25x = 540cm

⟹54x=540cm

⟹x=10

Therefore, the sides of the triangle are:

a=12×10=120cm

b=17×10=170cm

c=25×10=250cm

The semi-perimeter of the triangle is:

s=540cm2=270cm

Therefore, using Heron's Formula, the area of the triangle is:

A=s(s−a)(s−b)(s−c)

=270(270−120)(270−170)(270−250)

=270(150)(100)(20)

=81000000=9000cm2

Q6 An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Answer:

Given, the perimeter of an isosceles triangle is 30 cm and the length of the sides which are equal is 12 cm.

Let the third side length be 'a cm'.

Then, Perimeter=a+b+c

⇒30=a+12+12

⇒a=6cm

So, the semi-perimeter of the triangle is:

s=Perimeter2=12×30cm=15cm

Therefore, using Heron's Formula, the area of the triangle is:

A=s(s−a)(s−b)(s−c)

=15(15−6)(15−12)(15−12)

=15(9)(3)(3)

=915 cm2