NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclids Geometry

Class 9 Maths Chapter 5 Question Answers - Exercise: 5.1
Page number: 67-68
Total questions: 7

Question 1: Which of the following statements are true and which are false? Give reasons for your answers.

(i) Only one line can pass through a single point.

(ii) There are an infinite number of lines which pass through two distinct points.

(iii) A terminated line can be produced indefinitely on both sides.

(iv) If two circles are equal, then their radii are equal.

(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.

Answer:

i) FALSE
Because there is an infinite number of lines that can be passed through a single point. As shown in the diagram below

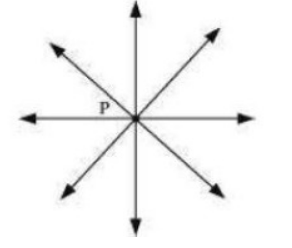
ii) FALSE
Because only one line can pass through two distinct points. As shown in the diagram below

iii) TRUE
Because a terminated line can be produced indefinitely on both sides. As shown in the diagram below

iv) TRUE
Because if two circles are equal, then their centre and circumferences will coincide and hence, the radii will also be equal.

v) TRUE
By Euclid’s first axiom, things which are equal to the same thing are equal to one another

Question 2: (i) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: A plane is a flat surface on which geometric figures are drawn.

Point: A point is a dimensionless dot which is drawn on a plane surface.

Line: A line is the collection of n number of points which can extend in both the directions and has only one dimension.
i) Parallel line:-
If the perpendicular distance between two lines is always constant and they never intersect with each other in a plane. Then, two lines are called parallel lines.

Question 2: (ii) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? (ii) perpendicular lines

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: A plane is a flat surface on which geometric figures are drawn.

Point: A point is a dimensionless dot which is drawn on a plane surface.

Line: A line is the collection of n number of points which can extend in both the directions and has only one dimension.
ii) perpendicular line:-
If two lines intersect with each other and make a right angle at the point of intersection. Then, two lines are called perpendicular lines.

Question 2: (iii) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? iii) line segment

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: A plane is a flat surface on which geometric figures are drawn.

Point: A point is a dimensionless dot which is drawn on a plane surface.

Line: A line is collection of n number of points which can extend in both the directions and has only one dimension.
iii) line segment : -
A straight line with two end points that cannot be extended further and has a definite length is called line segment

Question 2: (iv) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? iv) radius of circle

Answer:

iv) Radius of the circle : -
The distance between the centre of the circle and any point on the circumference of the circle is called the radius of a circle.

Q2. (v) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? v) square

Answer:

v) Square:-
A square is a quadrilateral in which all the four sides are equal and each internal angle is a right angle.

To define the square, we must know about quadrilateral.

Question 3: Consider two ‘postulates’ given below:

(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.

(ii) There exist at least three points that are not on the same line.

Do these postulates contain any undefined terms? Are these postulates consistent?

Do they follow from Euclid’s postulates? Explain.

Answer:

There are various undefined terms in the given postulates.:

1) There is no information given about the plane whether the points are in the same plane or not.

2) There is an infinite number of points lying in a plane. But here, the position of the point C has not been specified, whether it lies on the line segment joining AB or not.

Yes, these postulates are consistent when we deal with these two situations:

(i) Point C lies between and on the line segment joining A and B.

(ii) Point C does not lie on the line segment joining A and B.

No, they don’t follow from Euclid’s postulates. They follow the axioms.

Question 4: If a point C lies between two points A and B such that AC = BC, then prove that AC = 1/2 AB. Explain by drawing the figure.

Answer:

It is given that
AC = BC
Now,

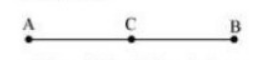
In the figure given above, AB coincides with AC + BC.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that AC + BC = AB
Now,
2AC = AB $(\because AC = BC )$
Therefore,
$AC = \frac{1}{2}AB$
Hence proved.

Question 5: In Question 4, point C is called a midpoint of the line segment AB. Prove that every line segment has one and only one midpoint.

Answer:

Let's assume that there are two midpoints C and D
Now,
If C is the midpoint then AC = BC
And
In the figure given above, AB coincides with AC + BC.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that AC + BC = AB
From this, we can say that
2AC = AB -(i)

Similarly,
If D is the midpoint then AD = BD
And
In the figure given above, AB coincides with AD + BD.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that AD + BD = AB
From this, we can say that
2AD = AB -(ii)
Now,
From equations (i) and (ii) we will get
AD = AC
and this is only possible when C and D are the same points
Hence, our assumption is wrong and there is only one midpoint of line segment AB.

Question 6: In Fig. 5.10, if AC = BD, then prove that AB = CD.

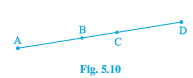
Answer:

From the figure given in the problem,
We can say that
AC = AB + BC and BD = BC + CD
Now,
It is given that AC = BD
Therefore,
AB + BC = BC + CD
Now, according to Euclid's axiom, when equals are subtracted from equals, the remainders are also equal. Subtracting BC from both sides.
We will get
AB + BC - BC = BC + CD - BC
AB = CD
Hence proved.

Question 7: Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)

Answer:

Axiom 5 states that the whole is greater than the part.
Let's take A = x + y + z, where A, x, y, z are all positive numbers
Now, we can clearly see that A > x , A > y , A > z
Hence, by this, we can say that the whole (A) is greater than the parts. (x, y, z).