NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

Edited By Komal Miglani | Updated on May 02, 2025 07:37 PM IST

Have you noticed how your score in a video game increases with each level you pass? Or how your savings grow month after month? Well, they don't just change randomly; they follow a certain pattern, that's what the Polynomials are all about. For example, a second-order polynomial (highest exponent 2) like $2 x^{2} + 5 x + 2$ can represent how your score increases as you progress through a game where $x$ is the game level. In the second chapter, you will find Polynomials, which are algebraic expressions of variables and coefficients - sound complex? Don't worry, we will break it down simply and logically, which will help you build your foundation in algebra. The NCERT Solutions for Polynomials guide learners through key concepts such as the Remainder and Factor Theorems with clarity.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

Polynomials Class 9 Questions And Answers PDF Free Download
Polynomials Class 9 Solutions - Important Formulae
NCERT Solutions for Class 9 Maths Chapter 2: Exercise Questions
Class 9 Maths NCERT Chapter 2: Extra Question
Approach to Solve Questions of Polynomials Class 9
Polynomials Class 9 Solutions - Exercise Wise
NCERT Solutions For Class 9 Maths - Chapter Wise
NCERT Solutions For Class 9 - Subject Wise
NCERT Class 9 Books and Syllabus

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

This article on NCERT solutions for class 9 Maths Chapter 2 Polynomials offers clear and step-by-step solutions for the exercise problems. Students who need the Polynomials class 9 solutions will find this article very useful. It covers all the important Class 9 Maths Chapter 2 question answers. According to the latest CBSE syllabus, these Polynomials class 9 ncert solutions are made by the Subject Matter Experts, ensuring that students can grasp the basic concepts effectively. NCERT Solutions for Class 9 and NCERT Solutions for other subjects and classes can be downloaded from our sources.

Polynomials Class 9 Questions And Answers PDF Free Download

Download PDF

Polynomials Class 9 Solutions - Important Formulae

The general form of a polynomial is: p(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0

where a0, a1, a2, …., an are constants, and an ≠ 0.

Every one-variable linear polynomial will contain a unique zero, which is a real number that is a zero of the zero polynomial, and a non-zero constant polynomial that does not have any zeros.

Remainder Theorem: If p(x) has a degree greater than or equal to 1, and you divide p(x) by the linear polynomial (x - a), the remainder will be p(a).

Factor Theorem: The linear polynomial $(x - a)$ will be a factor of the polynomial p(x) whenever p(a) = 0. Similarly, if $(x - a)$ is a factor of p(x), then p(a) = 0.

NCERT Solutions for Class 9 Maths Chapter 2: Exercise Questions

NCERT Polynomials class 9 solutions Exercise: 2.1
Page number: 29, Total questions: 5

Question 1: (i) Is the following expression a polynomial in one variable? State reasons for your answer.
$4 x^{2} - 3 x + 7$

Answer:

Yes, the polynomial $4 x^{2} - 3 x + 7$ has only one variable, which is $x$ .

Question 1: (ii) Is the following expression a polynomial in one variable? State reasons for your answer.
$y^{2} + \sqrt{2}$

Answer:

YES
Given polynomial has only one variable which is y.

Question 1: (iii) Is the following expression polynomial in one variable? State reasons for your answer.
$3 \sqrt{t} + t \sqrt{2}$

Answer:

NO
Because we can observe that the exponent of variable t in term $3 \sqrt{t}$ is $\frac{1}{2}$ which is not a whole number.
Therefore, this expression is not a polynomial.

Question 1: (iv) Is the following expression polynomial in one variable? State reasons for your answer.
$y + \frac{2}{y}$

Answer:

NO
Because we can observe that the exponent of variable y in term $\frac{2}{y}$ is $- 1$ which is not a whole number. Therefore this expression is not a polynomial.

Question 1: (v) Is the following expression polynomial in one variable? State reasons for your answer.
$x^{10} + y^{3} + t^{50}$

Answer:

NO
Because in the given polynomial $x^{10} + y^{3} + t^{50}$ there are 3 variables which are x, y, t. That's why this is a polynomial in three variables, not in one variable.

Question 2: (i) Write the coefficients of $x^{2}$ in the following: $2 + x^{2} + x$

Answer:

Coefficient of $x^{2}$ in polynomial $2 + x^{2} + x$ is 1.

Question 2: (ii) Write the coefficients of $x^{2}$ in the following: $2 - x^{2} + x^{3}$

Answer:

The coefficient of $x^{2}$ in polynomial $2 - x^{2} + x^{3}$ is -1.

Question 2: (iii) Write the coefficients of $x^{2}$ in the following: $\frac{π}{2} x^{2} + x$

Answer:

Coefficient of $x^{2}$ in polynomial $\frac{π}{2} x^{2} + x$ is $\frac{π}{2}$

Question 2: (iv) Write the coefficients of $x^{2}$ in the following: $\sqrt{2} x - 1$

Answer:

Coefficient of $x^{2}$ in polynomial $\sqrt{2} x - 1$ is 0

Question 3: Give one example each of a binomial of degree 35, and of a monomial of degree 100.

Answer:

The degree of a polynomial is the highest power of the variable in the polynomial.
In binomial, there are two terms
Therefore, a binomial of degree 35 is
Eg: $x^{35} + 1$
In a monomial, there is only one term in it.
Therefore, a monomial of degree 100 can be written as $y^{100}$

Question 4. (i) Write the degree the following polynomial: $5 x^{3} + 4 x^{2} + 7 x$

Answer:

The degree of a polynomial is the highest power of the variable in the polynomial.
Therefore, the degree of the polynomial $5 x^{3} + 4 x^{2} + 7 x$ is 3.

Question 4. (ii) Write the degree the following polynomial: $4 - y^{2}$

Answer:

The degree of a polynomial is the highest power of the variable in the polynomial.

Therefore, the degree of polynomial $4 - y^{2}$ is 2.

Question 4. (iii) Write the degree the following polynomial: $5 t - \sqrt{7}$

Answer:

The degree of a polynomial is the highest power of the variable in the polynomial.

Therefore, the degree of polynomial $5 t - \sqrt{7}$ is 1

Question 4. (iv) Write the degree the following polynomial: 3

Answer:

The degree of a polynomial is the highest power of the variable in the polynomial.

In this case, only a constant value 3 is there and the degree of a constant polynomial is always 0.

Question 5. (i) Classify the following as linear, quadratic and cubic polynomial: $x^{2} + x$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $x^{2} + x$ with degree 2

Therefore, it is a quadratic polynomial.

Question 5. (ii) Classify the following as linear, quadratic and cubic polynomials: $x - x^{3}$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial have its degrees as 1, 2, and 3, respectively
Given polynomial is $x - x^{3}$ with degree 3
Therefore, it is a cubic polynomial

Question 5 (iii) Classify the following as linear, quadratic and cubic polynomials: $y + y^{2} + 4$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial have its degrees as 1, 2, and 3, respectively

Given polynomial is $y + y^{2} + 4$ with degree 2.

Therefore, it is a quadratic polynomial.

Question 5. (iv) Classify the following as linear, quadratic and cubic polynomials: $1 + x$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $1 + x$ with degree 1

Therefore, it is linear polynomial

Question 5. (v) Classify the following as linear, quadratic and cubic polynomial: $3 t$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $3 t$ with degree 1

Therefore, it is a linear polynomial

Question 5. (vi) Classify the following as linear, quadratic and cubic polynomials: $r^{2}$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial have their degrees as 1, 2, and 3, respectively

Given polynomial is $r^{2}$ with degree 2

Therefore, it is a quadratic polynomial

Question 5. (vii) Classify the following as linear, quadratic and cubic polynomials: $7 x^{3}$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial have their degrees as 1, 2, and 3, respectively

Given polynomial is $7 x^{3}$ with degree 3

Therefore, it is a cubic polynomial.

Polynomials class 9 NCERT solutions Exercise: 2.2
Page number: 31-32, Total questions: 4

Question 1. (i) Find the value of the polynomial $5 x - 4 x^{2} + 3$ at $x = 0$

Answer:

Given polynomial is $5 x - 4 x^{2} + 3$

Now, at $x = 0$ value is

$\Rightarrow 5 (0) - 4 (0)^{2} + 3 = 0 - 0 + 3 = 3$

Therefore, value of polynomial $5 x - 4 x^{2} + 3$ at x = 0 is 3

Question 1. (ii) Find the value of the polynomial $5 x - 4 x^{2} + 3$ at $x = - 1$

Answer:

Given polynomial is $5 x - 4 x^{2} + 3$

Now, at $x = - 1$ value is

$\Rightarrow 5 (- 1) - 4 (- 1)^{2} + 3 = - 5 - 4 + 3 = - 6$

Therefore, value of polynomial $5 x - 4 x^{2} + 3$ at x = -1 is -6

Question 1. (iii) Find the value of the polynomial $5 x - 4 x^{2} + 3$ at $x = 2$

Answer:

Given polynomial is $5 x - 4 x^{2} + 3$

Now, at $x = 2$ value is

$\Rightarrow 5 (2) - 4 (2)^{2} + 3 = 10 - 16 + 3 = - 3$

Therefore, value of polynomial $5 x - 4 x^{2} + 3$ at x = 2 is -3

Question 2: (i) Find p(0) , p(1) and p(2) for each of the following polynomials: $p (y) = y^{2} - y + 1$

Answer:

Given polynomial is

$p (y) = y^{2} - y + 1$

Now,

$p (0) = (0)^{2} - 0 + 1 = 1$

$p (1) = (1)^{2} - 1 + 1 = 1$

$p (2) = (2)^{2} - 2 + 1 = 3$

Therefore, values of p(0) , p(1) and p(2) are 1 , 1 and 3 respectively .

Question 2: (ii) Find p(0) , p(1) and p(2) for each of the following polynomials: $p (t) = 2 + t + 2 t^{2} - t^{3}$

Answer:

Given polynomial is

$p (t) = 2 + t + 2 t^{2} - t^{3}$

Now,

$p (0) = 2 + 0 + 2 (0)^{2} - (0)^{3} = 2$

$p (1) = 2 + 1 + 2 (1)^{2} - (1)^{3} = 4$

$p (2) = 2 + 2 + 2 (2)^{2} - (2)^{3} = 4$

Therefore, values of p(0) , p(1) and p(2) are 2 , 4 and 4 respectively

Question 2: (iii) Find p(0), p(1) and p(2) for each of the following polynomials: $p (x) = x^{3}$

Answer:

Given polynomial is

$p (x) = x^{3}$

Now,

$p (0) = (0)^{3} = 0$

$p (1) = (1)^{3} = 1$

$p (2) = (2)^{3} = 8$
Therefore, values of p(0) , p(1) and p(2) are 0 , 1 and 8 respectively

Question 2: (iv) Find p(0), p(1) and p(2) for each of the following polynomials: $p (x) = (x - 1) (x + 1)$

Answer:

Given polynomial is
$p (x) = (x - 1) (x + 1) = x^{2} - 1$

Now,
$p (0) = (0)^{2} - 1 = - 1$

$p (1) = (1)^{2} - 1 = 0$

$p (2) = (2)^{2} - 1 = 3$

Therefore, values of p(0) , p(1) and p(2) are -1 , 0 and 3 respectively

Question 3. (i) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = 3 x + 1, x = - \frac{1}{3}$

Answer:

Given polynomial is $p (x) = 3 x + 1$

Now, at $x = - \frac{1}{3}$ it's value is

$p (- \frac{1}{3}) = 3 \times (- \frac{1}{3}) + 1 = - 1 + 1 = 0$

Therefore, yes $x = - \frac{1}{3}$ is a zero of polynomial $p (x) = 3 x + 1$

Question 3. (ii) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = 5 x - π, x = \frac{4}{5}$

Answer:

Given polynomial is $p (x) = 5 x - π$

Now, at $x = \frac{4}{5}$ it's value is

$p (\frac{4}{5}) = 5 \times (\frac{4}{5}) - π = 4 - π \neq 0$
Therefore, no $x = \frac{4}{5}$ is not a zero of polynomial $p (x) = 5 x - π$

Question 3. (iii) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = x^{2} - 1, x = 1, - 1$

Answer:

Given polynomial is $p (x) = x^{2} - 1$

Now, at x = 1 its value is

$p (1) = (1)^{2} - 1 = 1 - 1 = 0$

And at x = -1

$p (- 1) = (- 1)^{2} - 1 = 1 - 1 = 0$
Therefore, yes x = 1 , -1 are zeros of polynomial $p (x) = x^{2} - 1$

Question 3. (iv) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = (x + 1) (x - 2), x = - 1, 2$

Answer:

Given polynomial is $p (x) = (x + 1) (x - 2)$

Now, at x = 2 it's value is

$p (2) = (2 + 1) (2 - 2) = 0$

And at x = -1

$p (- 1) = (- 1 + 1) (- 1 - 2) = 0$

Therefore, yes x = 2 , -1 are zeros of polynomial $p (x) = (x + 1) (x - 2)$

Question 3. (v) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = x^{2} . x = 0$

Answer:

Given polynomial is $p (x) = x^{2}$

Now, at x = 0 it's value is

$p (0) = (0)^{2} = 0$

Therefore, yes x = 0 is a zeros of polynomial $p (x) = (x + 1) (x - 2)$

Question 3. (vi) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = l x + m, x = - \frac{m}{l}$

Answer:

Given polynomial is $p (x) = l x + m$

Now, at $x = - \frac{m}{l}$ it's value is

$p (- \frac{m}{l}) = l \times (- \frac{m}{l}) + m = - m + m = 0$

Therefore, yes $x = - \frac{m}{l}$ is a zeros of polynomial $p (x) = l x + m$

Question 3. (vii) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = 3 x^{2} - 1, x = - \frac{1}{\sqrt{3}}, \frac{2}{\sqrt{3}}$

Answer:

Given polynomial is $p (x) = 3 x^{2} - 1$

Now, at $x = - \frac{1}{\sqrt{3}}$ it's value is

$p (- \frac{1}{\sqrt{3}}) = 3 \times {(- \frac{1}{\sqrt{3}})}^{2} - 1 = 1 - 1 = 0$

And at $x = \frac{2}{\sqrt{3}}$

$p (\frac{2}{\sqrt{3}}) = 3 \times {(\frac{2}{\sqrt{3}})}^{2} - 1 = 4 - 1 = 3 \neq 0$

Therefore, $x = - \frac{1}{\sqrt{3}}$ is a zeros of polynomial $p (x) = 3 x^{2} - 1$ .

whereas $x = \frac{2}{\sqrt{3}}$ is not a zeros of polynomial $p (x) = 3 x^{2} - 1$

Question 3. (viii) Verify whether the following are zeroes of the polynomial, indicated against it. $p (x) = 2 x + 1, x = \frac{1}{2}$

Answer:

Given polynomial is $p (x) = 2 x + 1$

Now, at $x = \frac{1}{2}$ it's value is

$p (\frac{1}{2}) = 2 \times (\frac{1}{2}) + 1 = 1 + 1 = 2 \neq 0$

Therefore, $x = \frac{1}{2}$ is not a zeros of polynomial $p (x) = 2 x + 1$

Question 4. (i) Find the zero of the polynomial in each of the following cases: $p (x) = x + 5$

Answer:

Given polynomial is $p (x) = x + 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow x + 5 = 0$

$\Rightarrow x = - 5$

Therefore, x = -5 is the zero of polynomial $p (x) = x + 5$

Question 4. (ii) Find the zero of the polynomial in each of the following cases: $p (x) = x - 5$

Answer:

Given polynomial is $p (x) = x - 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow x - 5 = 0$

$\Rightarrow x = 5$

Therefore, x = 5 is a zero of polynomial $p (x) = x - 5$

Question 4. (iii) Find the zero of the polynomial in each of the following cases: $p (x) = 2 x + 5$

Answer:

Given polynomial is $p (x) = 2 x + 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow 2 x + 5 = 0$

$\Rightarrow x = - \frac{5}{2}$

Therefore, $x = - \frac{5}{2}$ is a zero of polynomial $p (x) = 2 x + 5$

Question 4. (iv) Find the zero of the polynomial in each of the following cases: $p (x) = 3 x - 2$

Answer:

Given polynomial is $p (x) = 3 x - 2$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow 3 x - 2 = 0$

$\Rightarrow x = \frac{2}{3}$
Therefore, $x = \frac{2}{3}$ is a zero of polynomial $p (x) = 3 x - 2$

Question 4. (v) Find the zero of the polynomial in each of the following cases: $p (x) = 3 x$

Answer:

Given polynomial is $p (x) = 3 x$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow 3 x = 0$

$\Rightarrow x = 0$

Therefore, $x = 0$ is a zero of polynomial $p (x) = 3 x$

Question 4. (vi) Find the zero of the polynomial in each of the following cases: $p (x) = a x, a \neq 0$

Answer:

Given polynomial is $p (x) = a x$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow a x = 0$

$\Rightarrow x = 0$

Therefore, $x = 0$ is a zero of polynomial $p (x) = a x$

Question 4. (vii) Find the zero of the polynomial in each of the following cases: $p (x) = c x + d, c \neq 0, c, d$ are real numbers

Answer:

Given polynomial is $p (x) = c x + d$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p (x) = 0$

$\Rightarrow c x + d = 0$

$\Rightarrow x = - \frac{d}{c}$

Therefore, $x = - \frac{d}{c}$ is a zero of polynomial $p (x) = c x + d$

Class 9 polynomials NCERT solutions Exercise: 2.3
Page number: 35-36, Total questions: 5

Question 1. (i) Determine which of the following polynomials has $(x + 1)$ a factor : $x^{3} + x^{2} + x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p (x) = x^{3} + x^{2} + x + 1$

Then, $p (- 1)$ must be equal to zero

Now,

$\Rightarrow p (- 1) = (- 1)^{3} + (- 1)^{2} - 1 + 1$

$\Rightarrow p (- 1) = - 1 + 1 - 1 + 1 = 0$

Therefore, $(x + 1)$ is a factor of polynomial $p (x) = x^{3} + x^{2} + x + 1$

Question 1. (ii) Determine which of the following polynomials has $(x + 1)$ a factor : $x^{4} + x^{3} + x^{2} + x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p (x) = x^{4} + x^{3} + x^{2} + x + 1$

Then, $p (- 1)$ must be equal to zero

Now,

$\Rightarrow p (- 1) = (- 1)^{4} + (- 1)^{3} + (- 1)^{2} - 1 + 1$

$\Rightarrow p (- 1) = 1 - 1 + 1 - 1 + 1 = 1 \neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p (x) = x^{4} + x^{3} + x^{2} + x + 1$

Question 1. (iii) Determine which of the following polynomials has $(x + 1)$ a factor : $x^{4} + 3 x^{3} + 3 x^{2} + x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p (x) = x^{4} + 3 x^{3} + 3 x^{2} + x + 1$

Then, $p (- 1)$ must be equal to zero

Now,

$\Rightarrow p (- 1) = (- 1)^{4} + 3 (- 1)^{3} + 3 (- 1)^{2} - 1 + 1$

$\Rightarrow p (- 1) = 1 - 3 + 3 - 1 + 1 = 1 \neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p (x) = x^{4} + 3 x^{3} + 3 x^{2} + x + 1$

Question 1. (iv) Determine which of the following polynomials has $(x + 1)$ a factor : $x^{3} - x^{2} - (2 + \sqrt{2}) x + \sqrt{2}$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p (x) = x^{3} - x^{2} - (2 + \sqrt{2}) x + \sqrt{2}$

Then, $p (- 1)$ must be equal to zero

Now,

$\Rightarrow p (- 1) = (- 1)^{3} - (- 1)^{2} - (2 + \sqrt{2}) (- 1) + \sqrt{2}$

$\Rightarrow p (- 1) = - 1 - 1 + 2 + \sqrt{2} + \sqrt{2} = 2 \sqrt{2} \neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p (x) = x^{3} - x^{2} - (2 + \sqrt{2}) x + \sqrt{2}$

Question 2: (i) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p (x) = 2 x^{3} + x^{2} - 2 x - 1, g (x) = x + 1$

Answer:

Zero of polynomial $g (x) = x + 1$ is $- 1$

If $g (x) = x + 1$ is factor of polynomial $p (x) = 2 x^{3} + x^{2} - 2 x - 1$

Then, $p (- 1)$ must be equal to zero

Now,

$\Rightarrow p (- 1) = 2 (- 1)^{3} + (- 1)^{2} - 2 (- 1) - 1$

$\Rightarrow p (- 1) = - 2 + 1 + 2 - 1 = 0$

Therefore, $g (x) = x + 1$ is factor of polynomial $p (x) = 2 x^{3} + x^{2} - 2 x - 1$

Question 2: (ii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p (x) = x^{3} + 3 x^{2} + 3 x + 1, g (x) = x + 2$

Answer:

Zero of polynomial $g (x) = x + 2$ is $- 2$

If $g (x) = x + 2$ is factor of polynomial $p (x) = x^{3} + 3 x^{2} + 3 x + 1$

Then, $p (- 2)$ must be equal to zero

Now,

$\Rightarrow p (- 2) = (- 2)^{3} + 3 (- 2)^{2} + 3 (- 2) + 1$

$\Rightarrow p (- 2) = - 8 + 12 - 6 + 1 = - 1 \neq 0$

Therefore, $g (x) = x + 2$ is not a factor of polynomial $p (x) = x^{3} + 3 x^{2} + 3 x + 1$

Question 2: (iii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p (x) = x^{3} - 4 x^{2} + x + 6, g (x) = x - 3$

Answer:

Zero of polynomial $g (x) = x - 3$ is $3$

If $g (x) = x - 3$ is factor of polynomial $p (x) = x^{3} - 4 x^{2} + x + 6$

Then, $p (3)$ must be equal to zero

Now,

$\Rightarrow p (3) = (3)^{3} - 4 (3)^{2} + 3 + 6$

$\Rightarrow p (3) = 27 - 36 + 3 + 6 = 0$

Therefore, $g (x) = x - 3$ is a factor of polynomial $p (x) = x^{3} - 4 x^{2} + x + 6$

Question 3. (i) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p (x) = x^{2} + x + k$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p (x) = x^{2} + x + k$

Then, $p (1)$ must be equal to zero

Now,

$\Rightarrow p (1) = (1)^{2} + 1 + k$

$\Rightarrow p (1) = 0$

$\Rightarrow 2 + k = 0$

$\Rightarrow k = - 2$

Therefore, the value of k is $- 2$

Question 3. (ii) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p (x) = 2 x^{2} + k x + \sqrt{2}$

Answer:

Zero of the polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p (x) = 2 x^{2} + k x + \sqrt{2}$

Then, $p (1)$ must be equal to zero

Now,

$\Rightarrow p (1) = 2 (1)^{2} + k (1) + \sqrt{2}$

$\Rightarrow p (1) = 0$

$\Rightarrow 2 + k + \sqrt{2} = 0$

$\Rightarrow k = - (2 + \sqrt{2})$

Therefore, the value of k is $- (2 + \sqrt{2})$

Question 3. (iii) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p (x) = k x^{2} - \sqrt{2} x + 1$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p (x) = k x^{2} - \sqrt{2} x + 1$

Then, $p (1)$ must be equal to zero

Now,

$\Rightarrow p (1) = k (1)^{2} - \sqrt{2} (1) + 1$

$\Rightarrow p (1) = 0$

$\Rightarrow k - \sqrt{2} + 1 = 0$

$\Rightarrow k = - 1 + \sqrt{2}$

Therefore, the value of k is $- 1 + \sqrt{2}$

Question 3. (iv) the value of k , if $x - 1$ is a factor of p(x) in the following case: $p (x) = k x^{2} - 3 x + k$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p (x) = k x^{2} - 3 x + k$

Then, $p (1)$ must be equal to zero

Now,

$\Rightarrow p (1) = k (1)^{2} - 3 (1) + k$

$\Rightarrow p (1) = 0$

$\Rightarrow k - 3 + k = 0$

$\Rightarrow k = \frac{3}{2}$
Therefore, value of k is $\frac{3}{2}$

Question 4. (i) Factorise : $12 x^{2} - 7 x + 1$

Answer:

Given polynomial is $12 x^{2} - 7 x + 1$

We need to factorise the middle term into two terms such that their product is equal to $12 \times 1 = 12$ and their sum is equal to $- 7$

We can solve it as

$\Rightarrow 12 x^{2} - 7 x + 1$

$\Rightarrow 12 x^{2} - 3 x - 4 x + 1$ $(∵ - 3 \times - 4 = 12 a n d - 3 + (- 4) = - 7)$

$\Rightarrow 3 x (4 x - 1) - 1 (4 x - 1)$

$\Rightarrow (3 x - 1) (4 x - 1)$

Question 4. (ii) Factorise : $2 x^{2} + 7 x + 3$

Answer:

Given polynomial is $2 x^{2} + 7 x + 3$

We need to factorise the middle term into two terms such that their product is equal to $2 \times 3 = 6$ and their sum is equal to $7$

We can solve it as

$\Rightarrow 12 x^{2} - 7 x + 1$

$\Rightarrow 2 x^{2} + 6 x + x + 3$ $(∵ 6 \times 1 = 6 a n d 6 + 1 = 7)$

$\Rightarrow 2 x (x + 3) + 1 (x + 3)$

$\Rightarrow (2 x + 1) (x + 3)$

Question 4. (iii) Factorise : $6 x^{2} + 5 x - 6$

Answer:

Given polynomial is $6 x^{2} + 5 x - 6$

We need to factorise the middle term into two terms such that their product is equal to $6 \times - 6 = - 36$ and their sum is equal to $5$

We can solve it as

$\Rightarrow 6 x^{2} + 5 x - 6$

$\Rightarrow 6 x^{2} + 9 x - 4 x - 6$ $(∵ 9 \times - 4 = - 36 a n d 9 + (- 4) = 5)$

$\Rightarrow 3 x (2 x + 3) - 2 (2 x + 3)$

$\Rightarrow (2 x + 3) (3 x - 2)$

Question 4. (iv) Factorise : $3 x^{2} - x - 4$

Answer:

Given polynomial is $3 x^{2} - x - 4$

We need to factorise the middle term into two terms such that their product is equal to $3 \times - 4 = - 12$ and their sum is equal to $- 1$

We can solve it as

$\Rightarrow 3 x^{2} - x - 4$

$\Rightarrow 3 x^{2} - 4 x + 3 x - 4$ $(∵ 3 \times - 4 = - 12 a n d 3 + (- 4) = - 1)$

$\Rightarrow x (3 x - 4) + 1 (3 x - 4)$

$\Rightarrow (x + 1) (3 x - 4)$

Question 5. (i) Factorise : $x^{3} - 2 x^{2} - x + 2$

Answer:

Given polynomial is $x^{3} - 2 x^{2} - x + 2$

Now, by hit and trial method we observed that $(x + 1)$ is one of the factors of the given polynomial.

By the long division method, we will get

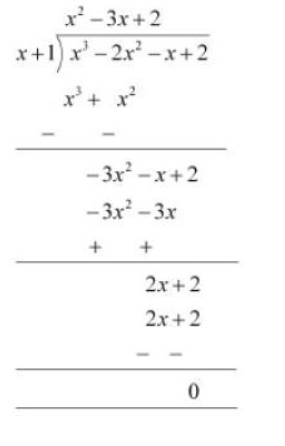
1639996302612

We know that Dividend = (Divisor × Quotient) + Remainder

$x^{3} - 2 x^{2} - x + 2 = (x + 1) (x^{2} - 3 x + 2) + 0$

$= (x + 1) (x^{2} - 2 x - x + 2)$

$= (x + 1) (x - 2) (x - 1)$

Therefore, on factorization of $x^{3} - 2 x^{2} - x + 2$ we will get $(x + 1) (x - 2) (x - 1)$

Question 5. (ii) Factorise : $x^{3} - 3 x^{2} - 9 x - 5$

Answer:

Given polynomial is $x^{3} - 3 x^{2} - 9 x - 5$

Now, by the hit-and-trial method, we observed that $(x + 1)$ is one of the factors of the given polynomial.

By the long division method, we will get

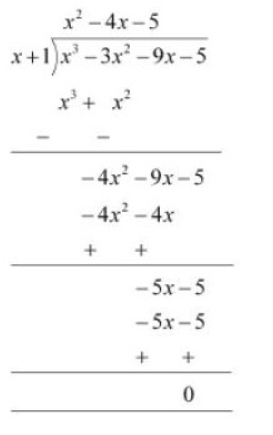
1639996323635

We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^{3} - 3 x^{2} - 9 x - 5 = (x + 1) (x^{2} - 4 x - 5)$

$= (x + 1) (x^{2} - 5 x + x - 5)$

$= (x + 1) (x - 5) (x + 1)$

Therefore, on factorization of $x^{3} - 3 x^{2} - 9 x - 5$ we will get $(x + 1) (x - 5) (x + 1)$

Question 5. (iii) Factorise : $x^{3} + 13 x^{2} + 32 x + 20$

Answer:

Given polynomial is $x^{3} + 13 x^{2} + 32 x + 20$

Now, by hit and trial method we observed that $(x + 1)$ is one of the factors of given polynomial.

By long division method, we will get

1639996347806

We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^{3} + 13 x^{2} + 32 x + 20 = (x + 1) (x^{2} + 12 x + 20)$

$= (x + 1) (x^{2} + 10 x + 2 x + 20)$

$= (x + 1) (x + 10) (x + 2)$

Therefore, on factorization of $x^{3} + 13 x^{2} + 32 x + 20$ we will get $(x + 1) (x + 10) (x + 2)$

Question 5. (iv) Factorise : $2 y^{3} + y^{2} - 2 y - 1$

Answer:

Given polynomial is $2 y^{3} + y^{2} - 2 y - 1$

Now, by hit and trial method we observed that $(y - 1)$ is one of the factors of the given polynomial.

By long division method, we will get

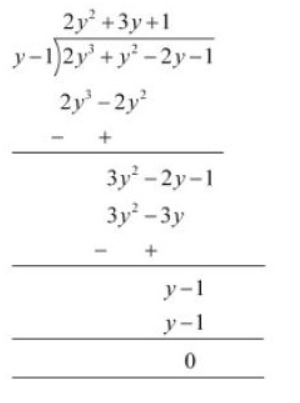
1639996378575

We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$2 y^{3} + y^{2} - 2 y - 1 = (y - 1) (2 y^{2} + 3 y + 1)$

$= (y - 1) (2 y^{2} + 2 y + y + 1)$

$= (y - 1) (2 y + 1) (y + 1)$

Therefore, on factorization of $2 y^{3} + y^{2} - 2 y - 1$ we will get $(y - 1) (2 y + 1) (y + 1)$ .

Class 9 maths chapter 2 question answer Exercise: 2.4
Page number: 40-42, Total questions: 16

Question 1. (i) Use suitable identities to find the following product: $(x + 4) (x + 10)$

Answer:

We will use identity

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

Put $a = 4 a n d b = 10$

$(x + 4) (x + 10) = x^{2} + (10 + 4) x + 10 \times 4$

$= x^{2} + 14 x + 40$

Therefore, $(x + 4) (x + 10)$ is equal to $x^{2} + 14 x + 40$

Question 1. (ii) Use suitable identities to find the following product: $(x + 8) (x - 10)$

Answer:

We will use identity

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

Put $a = 8 a n d b = - 10$

$(x + 8) (x - 10) = x^{2} + (- 10 + 8) x + 8 \times (- 10)$

$= x^{2} - 2 x - 80$

Therefore, $(x + 8) (x - 10)$ is equal to $x^{2} - 2 x - 80$

Question 1. (iii) Use suitable identities to find the following product: $(3 x + 4) (3 x - 5)$

Answer:

We can write $(3 x + 4) (3 x - 5)$ as

$(3 x + 4) (3 x - 5) = 9 (x + \frac{4}{3}) (x - \frac{5}{3})$

We will use identity

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

Put $a = \frac{4}{3} a n d b = - \frac{5}{3}$

$9 (x + \frac{4}{3}) (x - \frac{5}{3}) = 9 (x^{2} + (\frac{4}{3} - \frac{5}{3}) x + \frac{4}{3} \times (- \frac{5}{3}))$

$= 9 x^{2} - 3 x - 20$

Therefore, $(3 x + 4) (3 x - 5)$ is equal to $9 x^{2} - 3 x - 20$

Question 1. (iv) Use suitable identities to find the following product: $(y^{2} + \frac{3}{2}) (y^{2} - \frac{3}{2})$

Answer:

We will use identity

$(x + a) (x - a) = x^{2} - a^{2}$

Put $x = y^{2} a n d a = \frac{3}{2}$

$(y^{2} + \frac{3}{2}) (y^{2} - \frac{3}{2}) = {(y^{2})}^{2} - {(\frac{3}{2})}^{2}$

$= y^{4} - \frac{9}{4}$

Therefore, $(y^{2} + \frac{3}{2}) (y^{2} - \frac{3}{2})$ is equal to $y^{4} - \frac{9}{4}$

Question 1. (v) Use suitable identities to find the following product: $(3 - 2 x) (3 + 2 x)$

Answer:

We can write $(3 - 2 x) (3 + 2 x)$ as

$(3 - 2 x) (3 + 2 x) = - 4 (x - \frac{3}{2}) (x + \frac{3}{2})$

We will use identity

$(x + a) (x - a) = x^{2} - a^{2}$

Put $a = \frac{3}{2}$

$- 4 (x + \frac{3}{2}) (x - \frac{3}{2}) = - 4 ({(x)}^{2} - {(\frac{3}{2})}^{2})$

$= 9 - 4 x^{2}$

Therefore, $(3 - 2 x) (3 + 2 x)$ is equal to $9 - 4 x^{2}$

Question 2: (i) Evaluate the following product without multiplying directly: $103 \times 107$

Answer:

We can rewrite $103 \times 107$ as

$\Rightarrow 103 \times 107 = (100 + 3) \times (100 + 7)$

We will use identity

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

Put $x = 100, a = 3 a n d b = 7$

$(100 + 3) \times (100 + 7) = (100)^{2} + (3 + 7) 100 + 3 \times 7$

$= 10000 + 1000 + 21 = 11021$

Therefore, value of $103 \times 107$ is $11021$

Question 2: (ii) Evaluate the following product without multiplying directly: $95 \times 96$

Answer:

We can rewrite $95 \times 96$ as

$\Rightarrow 95 \times 96 = (100 - 5) \times (100 - 4)$

We will use identity

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

Put $x = 100, a = - 5 a n d b = - 4$

$(100 - 5) \times (100 - 4) = (100)^{2} + (- 5 - 4) 100 + (- 5) \times (- 4)$

$= 10000 - 900 + 20 = 9120$

Therefore, value of $95 \times 96$ is $9120$

Question 2: (iii) Evaluate the following product without multiplying directly: $104 \times 96$

Answer:

We can rewrite $104 \times 96$ as

$\Rightarrow 104 \times 96 = (100 + 4) \times (100 - 4)$

We will use identity

$(x + a) (x - a) = x^{2} - a^{2}$

Put $x = 100 a n d a = 4$

$(100 + 4) \times (100 - 4) = (100)^{2} - (4)^{2}$

$= 10000 - 16 = 9984$

Therefore, value of $104 \times 96$ is $9984$

Question 3. (i) Factorise the following using appropriate identities: $9 x^{2} + 6 x y + y^{2}$

Answer:

We can rewrite $9 x^{2} + 6 x y + y^{2}$ as

$\Rightarrow 9 x^{2} + 6 x y + y^{2} = (3 x)^{2} + 2 \times 3 x \times y + (y)^{2}$

Using identity $\Rightarrow (a + b)^{2} = (a)^{2} + 2 \times a \times b + (b)^{2}$

Here, $a = 3 x a n d b = y$

Therefore,

$9 x^{2} + 6 x y + y^{2} = (3 x + y)^{2} = (3 x + y) (3 x + y)$

Question 3. (ii) Factorise the following using appropriate identities: $4 y^{2} - 4 y + 1$

Answer:

We can rewrite $4 y^{2} - 4 y + 1$ as

$\Rightarrow 4 y^{2} - 4 y + 1 = (2 y)^{2} - 2 \times 2 y \times 1 + (1)^{2}$

Using identity $\Rightarrow (a - b)^{2} = (a)^{2} - 2 \times a \times b + (b)^{2}$

Here, $a = 2 y a n d b = 1$

Therefore,

$4 y^{2} - 4 y + 1 = (2 y - 1)^{2} = (2 y - 1) (2 y - 1)$

Question 3. (iii) Factorise the following using appropriate identities: $x^{2} - \frac{y^{2}}{100}$

Answer:

We can rewrite $x^{2} - \frac{y^{2}}{100}$ as

$\Rightarrow x^{2} - \frac{y^{2}}{100} = (x)^{2} - {(\frac{y}{10})}^{2}$

Using identity $\Rightarrow a^{2} - b^{2} = (a - b) (a + b)$

Here, $a = x a n d b = \frac{y}{10}$

Therefore,

$x^{2} - \frac{y^{2}}{100} = (x - \frac{y}{10}) (x + \frac{y}{10})$

Question 4. (i) Expand each of the following, using suitable identities: $(x + 2 y + 4 z)^{2}$

Answer:

Given is $(x + 2 y + 4 z)^{2}$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = x, b = 2 y a n d c = 4 z$

Therefore,

$(x + 2 y + 4 z)^{2} = (x)^{2} + (2 y)^{2} + (4 z)^{2} + 2. x .2 y + 2.2 y .4 z + 2.4 z . x$

$= x^{2} + 4 y^{2} + 16 z^{2} + 4 x y + 16 y z + 8 z x$

Question 4. (ii) Expand each of the following, using suitable identities: $(2 x - y + z)^{2}$

Answer:

Given is $(2 x - y + z)^{2}$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = 2 x, b = - y a n d c = z$

Therefore,

$(2 x - y + z)^{2} = (2 x)^{2} + (- y)^{2} + (z)^{2} + 2.2 x . (- y) + 2. (- y) . z + 2. z .2 x$

$= 4 x^{2} + y^{2} + z^{2} - 4 x y - 2 y z + 4 z x$

Question 4. (iii) Expand each of the following, using suitable identities: $(- 2 x + 3 y + 2 z)^{2}$

Answer:

Given is $(- 2 x + 3 y + 2 z)^{2}$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = - 2 x, b = 3 y a n d c = 2 z$

Therefore,

$(- 2 x + 3 y + 2 z)^{2} = (- 2 x)^{2} + (3 y)^{2} + (2 z)^{2} + 2. (- 2 x) .3 y + 2.3 y .2 z + 2. z . (- 2 x)$

$= 4 x^{2} + 9 y^{2} + 4 z^{2} - 12 x y + 12 y z - 8 z x$

Question 4. (iv) Expand each of the following, using suitable identities: $(3 a - 7 b - c)^{2}$

Answer:

Given is $(3 a - 7 b - c)^{2}$

We will Use identity

$(x + y + z)^{2} = x^{2} + y^{2} + z^{2} + 2 x y + 2 y z + 2 z x$

Here, $x = 3 a, y = - 7 b a n d z = - c$

Therefore,

$(3 a - 7 b - c)^{2} = (3 a)^{2} + (- 7 b)^{2} + (- c)^{2} + 2.3 a . (- 7 b) + 2. (- 7 b) . (- c) + 2. (- c)$ $.3 a$

$= 9 a^{2} + 49 b^{2} + c^{2} - 42 a b + 14 b c - 6 c a$

Question 4. (v) Expand each of the following, using suitable identities: $(- 2 x + 5 y - 3 z)^{2}$

Answer:

Given is $(- 2 x + 5 y - 3 z)^{2}$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = - 2 x, b = 5 y a n d c = - 3 z$

Therefore,

$(- 2 x + 5 y - 3 z)^{2}$ $= (- 2 x)^{2} + (5 y)^{2} + (- 3 z)^{2} + 2. (- 2 x) .5 y + 2.5 y . (- 3 z) + 2. (- 3 z) . (- 2 x)$

$= 4 x^{2} + 25 y^{2} + 9 z^{2} - 20 x y - 30 y z + 12 z x$

Question 4. (vi) Expand each of the following, using suitable identities: ${[\frac{1}{4} a - \frac{1}{2} b + 1]}^{2}$

Answer:

Given is ${[\frac{1}{4} a - \frac{1}{2} b + 1]}^{2}$

We will Use identity

$(x + y + z)^{2} = x^{2} + y^{2} + z^{2} + 2 x y + 2 y z + 2 z x$

Here, $x = \frac{a}{4}, y = - \frac{b}{2} a n d z = 1$

Therefore,

${[\frac{1}{4} a - \frac{1}{2} b + 1]}^{2}$ $= {(\frac{a}{4})}^{2} + {(- \frac{b}{2})}^{2} + (1)^{2} + 2. (\frac{a}{4}) . (- \frac{b}{2}) + 2. (- \frac{b}{2}) .1 + 2.1 . (\frac{a}{4})$

$= \frac{a^{2}}{16} + \frac{b^{2}}{4} + 1 - \frac{a b}{4} - b + \frac{a}{2}$

Question 5. (i) Factorise: $4 x^{2} + 9 y^{2} + 16 z^{2} + 12 x y - 24 y z - 16 x z$

Answer:

We can rewrite $4 x^{2} + 9 y^{2} + 16 z^{2} + 12 x y - 24 y z - 16 x z$ as

$\Rightarrow 4 x^{2} + 9 y^{2} + 16 z^{2} + 12 x y - 24 y z - 16 x z$ $= (2 x)^{2} + (3 y)^{2} + (- 4 z)^{2} + 2.2 x .3 y + 2.3 y . (- 4 z) + 2. (- 4 z) .2 x$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = 2 x, b = 3 y a n d c = - 4 z$

Therefore,

$4 x^{2} + 9 y^{2} + 16 z^{2} + 12 x y - 24 y z - 16 x z = (2 x + 3 y - 4 z)^{2}$

$= (2 x + 3 y - 4 z) (2 x + 3 y - 4 z)$

Question 5. (ii) Factorise: $2 x^{2} + y^{2} + 8 z^{2} - 2 \sqrt{2} x y + 4 \sqrt{2} y z - 8 x z$

Answer:

We can rewrite $2 x^{2} + y^{2} + 8 z^{2} - 2 \sqrt{2} x y + 4 \sqrt{2} y z - 8 x z$ as

$\Rightarrow 2 x^{2} + y^{2} + 8 z^{2} - 2 \sqrt{2} x y + 4 \sqrt{2} y z - 8 x z$ $= (- \sqrt{2} x)^{2} + (y)^{2} + (2 \sqrt{2} z)^{2} + 2. (- \sqrt{2}) . y + 2. y .2 \sqrt{2} z + 2. (- \sqrt{2} x) .2 \sqrt{2} z$

We will Use identity

$(a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

Here, $a = - \sqrt{2} x, b = y a n d c = 2 \sqrt{2} z$

Therefore,

$2 x^{2} + y^{2} + 8 z^{2} - 2 \sqrt{2} x y + 4 \sqrt{2} y z - 8 x z = (- \sqrt{2} x + y + 2 \sqrt{2} z)^{2}$

$= (- \sqrt{2} x + y + 2 \sqrt{2} z) (- \sqrt{2} x + y + 2 \sqrt{2} z)$

Question 6 (i) Write the following cubes in expanded form: $(2 x + 1)^{3}$

Answer:

Given is $(2 x + 1)^{3}$

We will use identity

$(a + b)^{3} = a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Here, $a = 2 x a n d b = 1$

Therefore,

$(2 x + 1)^{3} = (2 x)^{3} + (1)^{3} + 3. (2 x)^{2} .1 + 3.2 x . (1)^{2}$

$= 8 x^{3} + 1 + 12 x^{2} + 6 x$

Question 6. (ii) Write the following cube in expanded form: $(2 a - 3 b)^{3}$

Answer:

Given is $(2 a - 3 b)^{3}$

We will use identity

$(x - y)^{3} = x^{3} - y^{3} - 3 x^{2} y + 3 x y^{2}$

Here, $x = 2 a a n d y = 3 b$

Therefore,

$(2 a - 3 b)^{3} = (2 a)^{3} - (3 b)^{3} - 3. (2 a)^{2} .3 b + 3.2 a . (3 b)^{2}$

$= 8 a^{3} - 9 b^{3} - 36 a^{2} b + 54 a b^{2}$

Question 6. (iii) Write the following cube in expanded form: ${[\frac{3}{2} x + 1]}^{3}$

Answer:

Given is ${[\frac{3}{2} x + 1]}^{3}$

We will use identity

$(a + b)^{3} = a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Here, $a = \frac{3 x}{2} a n d b = 1$

Therefore,

${(\frac{3 x}{2} + 1)}^{3} = {(\frac{3 x}{2})}^{3} + (1)^{3} + 3. {(\frac{3 x}{2})}^{2} .1 + 3. \frac{3 x}{2} . (1)^{2}$

$= \frac{27 x^{3}}{8} + 1 + \frac{27 x^{2}}{4} + \frac{9 x}{2}$

Question 6. (iv) Write the following cube in expanded form: ${[x - \frac{2}{3} y]}^{3}$

Answer:

Given is ${[x - \frac{2}{3} y]}^{3}$

We will use identity

$(a - b)^{3} = a^{3} - b^{3} - 3 a^{2} b + 3 a b^{2}$

Here, $a = x a n d b = \frac{2 y}{3}$

Therefore,

${[x - \frac{2}{3} y]}^{3} = x^{3} - {(\frac{2 y}{3})}^{3} - 3. x^{2} . \frac{2 y}{3} + 3. x . {(\frac{2 y}{3})}^{2}$

$= x^{3} - \frac{8 y^{3}}{27} - 2 x^{2} y + \frac{4 x y^{2}}{3}$

Question 7. (i) Evaluate the following using suitable identities: $(99)^{3}$

Answer:

We can rewrite $(99)^{3}$ as

$\Rightarrow (99)^{3} = (100 - 1)^{3}$

We will use identity

$(a - b)^{3} = a^{3} - b^{3} - 3 a^{2} b + 3 a b^{2}$

Here, $a = 100 a n d b = 1$

Therefore,

$(100 - 1)^{1} = (100)^{3} - (1)^{3} - 3. (100)^{2} .1 + 3.100 {.1}^{2}$

$= 1000000 - 1 - 30000 + 300 = 970299$

Question 7. (ii) Evaluate the following using suitable identities: $(102)^{3}$

Answer:

We can rewrite $(102)^{3}$ as

$\Rightarrow (102)^{3} = (100 + 2)^{3}$

We will use identity

$(a + b)^{3} = a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Here, $a = 100 a n d b = 2$

Therefore,

$(100 + 2)^{1} = (100)^{3} + (2)^{3} + 3. (100)^{2} .2 + 3.100 {.2}^{2}$

$= 1000000 + 8 + 60000 + 1200 = 1061208$

Question 7. (iii) Evaluate the following using suitable identities: $(998)^{3}$

Answer:

We can rewrite $(998)^{3}$ as

$\Rightarrow (998)^{3} = (1000 - 2)^{3}$

We will use identity

$(a - b)^{3} = a^{3} - b^{3} - 3 a^{2} b + 3 a b^{2}$

Here, $a = 1000 a n d b = 2$

Therefore,

$(1000 - 2)^{1} = (1000)^{3} - (2)^{3} - 3. (0100)^{2} .2 + 3.1000 {.2}^{2}$

$= 1000000000 - 8 - 6000000 + 12000 = 994011992$

Question 8. (i) Factorise the following: $8 a^{3} + b^{3} + 12 a^{2} b + 6 a b^{2}$

Answer:

We can rewrite $8 a^{3} + b^{3} + 12 a^{2} b + 6 a b^{2}$ as

$\Rightarrow 8 a^{3} + b^{3} + 12 a^{2} b + 6 a b^{2}$ $= (2 a)^{3} + (b)^{3} + 3. (2 a)^{2} . b + 3.2 a . (b)^{2}$

We will use identity

$(x + y)^{3} = x^{3} + y^{3} + 3 x^{2} y + 3 x y^{2}$

Here, $x = 2 a a n d y = b$

Therefore,

$8 a^{3} + b^{3} + 12 a^{2} b + 6 a b^{2} = (2 a + b)^{3}$

$= (2 a + b) (2 a + b) (2 a + b)$

Question 8. (ii) Factorise the following: $8 a^{3} - b^{3} - 12 a^{2} b + 6 a b^{2}$

Answer:

We can rewrite $8 a^{3} - b^{3} - 12 a^{2} b + 6 a b^{2}$ as

$\Rightarrow 8 a^{3} - b^{3} - 12 a^{2} b + 6 a b^{2}$ $= (2 a)^{3} - (b)^{3} - 3. (2 a)^{2} . b + 3.2 a . (b)^{2}$

We will use identity

$(x - y)^{3} = x^{3} - y^{3} - 3 x^{2} y + 3 x y^{2}$

Here, $x = 2 a a n d y = b$

Therefore,

$8 a^{3} - b^{3} - 12 a^{2} b + 6 a b^{2} = (2 a - b)^{3}$

$= (2 a - b) (2 a - b) (2 a - b)$

Question 8. (iii) Factorise the following: $27 - 125 a^{3} - 135 a + 225 a^{2}$

Answer:

We can rewrite $27 - 125 a^{3} - 135 a + 225 a^{2}$ as

$\Rightarrow 27 - 125 a^{3} - 135 a + 225 a^{2}$ $= (3)^{3} - (25 a)^{3} - 3. (3)^{2} .5 a + 3.3 . (5 a)^{2}$

We will use identity

$(x - y)^{3} = x^{3} - y^{3} - 3 x^{2} y + 3 x y^{2}$

Here, $x = 3 a n d y = 5 a$

Therefore,

$27 - 125 a^{3} - 135 a + 225 a^{2} = (3 - 5 a)^{3}$

$= (3 - 5 a) (3 - 5 a) (3 - 5 a)$

Question 8. (iv) Factorise the following: $64 a^{3} - 27 b^{3} - 144 a^{2} b + 108 a b^{2}$

Answer:

We can rewrite $64 a^{3} - 27 b^{3} - 144 a^{2} b + 108 a b^{2}$ as

$\Rightarrow 64 a^{3} - 27 b^{3} - 144 a^{2} b + 108 a b^{2}$ $= (4 a)^{3} - (3 b)^{3} - 3. (4 a)^{2} .3 b + 3.4 a . (3 b)^{2}$

We will use identity

$(x - y)^{3} = x^{3} - y^{3} - 3 x^{2} y + 3 x y^{2}$

Here, $x = 4 a a n d y = 3 b$

Therefore,

$64 a^{3} - 27 b^{3} - 144 a^{2} b + 108 a b^{2} = (4 a - 3 b)^{2}$

$= (4 a - 3 b) (4 a - 3 b) (4 a - 3 b)$

Question 8. (v) Factorise the following: $27 p^{3} - \frac{1}{216} - \frac{9}{2} p^{2} + \frac{1}{4} p$

Answer:

We can rewrite $27 p^{3} - \frac{1}{216} - \frac{9}{2} p^{2} + \frac{1}{4} p$ as

$\Rightarrow 27 p^{3} - \frac{1}{216} - \frac{9}{2} p^{2} + \frac{1}{4} p$ $= (3 p)^{3} - {(\frac{1}{6})}^{3} - 3. (3 p)^{2} . \frac{1}{6} + 3.3 p . {(\frac{1}{6})}^{2}$

We will use identity

$(x - y)^{3} = x^{3} - y^{3} - 3 x^{2} y + 3 x y^{2}$

Here, $x = 3 p a n d y = \frac{1}{6}$

Therefore,

$27 p^{3} - \frac{1}{216} - \frac{9}{2} p^{2} + \frac{1}{4} p = {(3 p - \frac{1}{6})}^{3}$

$= (3 p - \frac{1}{6}) (3 p - \frac{1}{6}) (3 p - \frac{1}{6})$

Question 9. (i) Verify: $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$

Answer:

We know that

$(x + y)^{3} = x^{3} + y^{3} + 3 x y (x + y)$

Now,

$\Rightarrow x^{3} + y^{3} = (x + y)^{3} - 3 x y (x + y)$

$\Rightarrow x^{3} + y^{3} = (x + y) ((x + y)^{2} - 3 x y)$

$\Rightarrow x^{3} + y^{3} = (x + y) (x^{2} + y^{2} + 2 x y - 3 x y)$ $(∵ (a + b)^{2} = a^{2} + b^{2} + 2 a b)$

$\Rightarrow x^{3} + y^{3} = (x + y) (x^{2} + y^{2} - x y)$

Hence proved.

Question 9. (ii) Verify: $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$

Answer:

We know that

$(x - y)^{3} = x^{3} - y^{3} - 3 x y (x - y)$

Now,

$\Rightarrow x^{3} - y^{3} = (x - y)^{3} + 3 x y (x - y)$

$\Rightarrow x^{3} - y^{3} = (x - y) ((x - y)^{2} + 3 x y)$

$\Rightarrow x^{3} - y^{3} = (x - y) (x^{2} + y^{2} - 2 x y + 3 x y)$ $(∵ (a - b)^{2} = a^{2} + b^{2} - 2 a b)$

$\Rightarrow x^{3} - y^{3} = (x - y) (x^{2} + y^{2} + x y)$

Hence proved.

Question 10. (i) Factorise the following: $27 y^{3} + 125 z^{3}$

Answer:

We know that

$a^{3} + b^{3} = (a + b) (a^{2} + b^{2} - a b)$

Now, we can write $27 y^{3} + 125 z^{3}$ as

$\Rightarrow 27 y^{3} + 125 z^{3} = (3 y)^{3} + (5 z)^{3}$

Here, $a = 3 y a n d b = 5 z$

Therefore,

$27 y^{3} + 125 z^{3} = (3 y + 5 z) ((3 y)^{2} + (5 z)^{2} - 3 y .5 z)$

$27 y^{3} + 125 z^{3} = (3 y + 5 z) (9 y^{2} + 25 z^{2} - 15 y z)$

Question 10. (ii) Factorise the following: $64 m^{3} - 343 n^{3}$

Answer:

We know that

$a^{3} - b^{3} = (a - b) (a^{2} + b^{2} + a b)$

Now, we can write $64 m^{3} - 343 n^{3}$ as

$\Rightarrow 64 m^{3} - 343 n^{3} = (4 m)^{3} - (7 n)^{3}$

Here, $a = 4 m a n d b = 7 n$

Therefore,

$64 m^{3} - 343 n^{3} = (4 m - 7 n) ((4 m)^{2} + (7 n)^{2} + 4 m .7 n)$

$64 m^{3} - 343 n^{3} = (4 m - 7 n) (16 m^{2} + 49 n^{2} + 28 m n)$

Question 11. Factorise: $27 x^{3} + y^{3} + z^{3} - 9 x y z$

Answer:

Given is $27 x^{3} + y^{3} + z^{3} - 9 x y z$

Now, we know that

$a^{3} + b^{3} + c^{3} - 3 a b c = (a + b + c) (a^{2} + b^{2} + c^{2} - a b - b c - c a)$

Now, we can write $27 x^{3} + y^{3} + z^{3} - 9 x y z$ as

$\Rightarrow 27 x^{3} + y^{3} + z^{3} - 9 x y z$ $= (3 x)^{3} + (y)^{3} + (z)^{3} - 3.3 x . y . z$

Here, $a = 3 x, b = y a n d c = z$

Therefore,

$27 x^{3} + y^{3} + z^{3} - 9 x y z$ $= (3 x + y + z) ((3 x)^{2} + (y)^{2} + (z)^{2} - 3 x . y - y . z - z .3 x)$

$= (3 x + y + z) (9 x^{2} + y^{2} + z^{2} - 3 x y - y z - 3 z x)$ .

Question 12. Verify that $x^{3} + y^{3} + z^{3} - 3 x y z = \frac{1}{2} (x + y + z) [(x - y)^{2} + (y - z)^{2} + (z - x)^{2}]$

Answer:

We know that

$x^{3} + y^{3} + z^{3} - 3 x y z = (x + y + z) (x^{2} + y^{2} + z^{2} - x y - y z - z x)$

Now, multiply and divide the R.H.S. by 2

$x^{3} + y^{3} + z^{3} - 3 x y z = \frac{1}{2} (x + y + z) (2 x^{2} + 2 y^{2} + 2 z^{2} - 2 x y - 2 y z - 2 z x)$

$= \frac{1}{2} (x + y + z) (x^{2} + y^{2} - 2 x y + x^{2} + z^{2} - 2 z x + y^{2} + z^{2} - 2 y z)$

$= \frac{1}{2} (x + y + z) ((x - y)^{2} + (y - z)^{2} + (z - x)^{2})$ $(∵ a^{2} + b^{2} - 2 a b = (a - b)^{2})$

Hence proved.

Question 13. If $x + y + z = 0$ , show that $x^{3} + y^{3} + z^{3} = 3 x y z$ .

Answer:

We know that

$x^{3} + y^{3} + z^{3} - 3 x y z = (x + y + z) (x^{2} + y^{2} + z^{2} - x y - y z - z x)$

Now, It is given that $x + y + z = 0$

Therefore,

$x^{3} + y^{3} + z^{3} - 3 x y z = 0 (x^{2} + y^{2} + z^{2} - x y - y z - z x)$

$x^{3} + y^{3} + z^{3} - 3 x y z = 0$

$x^{3} + y^{3} + z^{3} = 3 x y z$

Hence proved.

Question 14. (i) Without actually calculating the cubes, find the value of each of the following: $(- 12)^{3} + (7)^{3} + (5)^{3}$

Answer:

Given is $(- 12)^{3} + (7)^{3} + (5)^{3}$

We know that

If $x + y + z = 0$ then , $x^{3} + y^{3} + z^{3} = 3 x y z$

Here, $x = - 12, y = 7 a n d z = 5$

$\Rightarrow x + y + z = - 12 + 7 + 5 = 0$

Therefore,

$(- 12)^{3} + (7)^{3} + (5)^{3} = 3 \times (- 12) \times 7 \times 5 = - 1260$

Therefore, value of $(- 12)^{3} + (7)^{3} + (5)^{3}$ is $- 1260$

Question 14. (ii) Without actually calculating the cubes, find the value of the following: $(28)^{3} + (- 15)^{3} + (- 13)^{3}$

Answer:

Given is $(28)^{3} + (- 15)^{3} + (- 13)^{3}$

We know that

If $x + y + z = 0$ then , $x^{3} + y^{3} + z^{3} = 3 x y z$

Here, $x = 28, y = - 15 a n d z = - 13$

$\Rightarrow x + y + z = 28 - 15 - 13 = 0$

Therefore,

$(28)^{3} + (- 15)^{3} + (- 13)^{3} = 3 \times (28) \times (- 15) \times (- 13) = 16380$

Therefore, value of $(28)^{3} + (- 15)^{3} + (- 13)^{3}$ is $16380$

Question 15. (i) Give possible expressions for the length and breadth of the following rectangle, in which its area is given: $25 a^{2} - 35 a + 12$

Answer:

We know that

Area of rectangle is = $l e n g t h \times b r e a d t h$

It is given that area = $25 a^{2} - 35 a + 12$

Now, by splitting middle term method

$\Rightarrow 25 a^{2} - 35 a + 12 = 25 a^{2} - 20 a - 15 a + 12$

$= 5 a (5 a - 4) - 3 (5 a - 4)$

$= (5 a - 3) (5 a - 4)$
Therefore, two answers are possible

case (i) :- Length = $(5 a - 4)$ and Breadth = $(5 a - 3)$

case (ii) :- Length = $(5 a - 3)$ and Breadth = $(5 a - 4)$

Question 15. (ii) Give possible expressions for the length and breadth of the following rectangle, in which its area is given: $35 y^{2} + 13 y - 12$

Answer:

We know that

Area of rectangle is = $l e n g t h \times b r e a d t h$

It is given that area = $35 y^{2} + 13 y - 12$

Now, by splitting the middle term method

$\Rightarrow 35 y^{2} + 13 y - 12 = 35 y^{2} + 28 y - 15 y - 12$

$= 7 y (5 y + 4) - 3 (5 y + 4)$

$= (7 y - 3) (5 y + 4)$

Therefore, two answers are possible

case (i) :- Length = $(5 y + 4)$ and Breadth = $(7 y - 3)$

case (ii) :- Length = $(7 y - 3)$ and Breadth = $(5 y + 4)$

Question 16. (i) What are the possible expressions for the dimensions of the cuboid whose volumes is given below Volume : $3 x^{2} - 12 x$ ?

Answer:

We know that

Volume of cuboid is = $l e n g t h \times b r e a d t h \times h e i g h t$

It is given that volume = $3 x^{2} - 12 x$

Now,

$\Rightarrow 3 x^{2} - 12 x = 3 \times x \times (x - 4)$

Therefore,one of the possible answer is possible

Length = $3$ and Breadth = $x$ and Height = $(x - 4)$

Question 16: (ii) What are the possible expressions for the dimensions of the cuboid whose volumes is given below Volume : $12 k y^{2} + 8 k y - 20 k$ ?

Answer:

We know that

Volume of cuboid is = $l e n g t h \times b r e a d t h \times h e i g h t$

It is given that volume = $12 k y^{2} + 8 k y - 20 k$

Now,

$\Rightarrow 12 k y^{2} + 8 k y - 20 k = k (12 y^{2} + 8 y - 20)$

$= k (12 y^{2} + 20 y - 12 y - 20)$

$= k (4 y (3 y + 5) - 4 (3 y + 5))$

$= k (3 y + 5) (4 y - 4)$

$= 4 k (3 y + 5) (y - 1)$

Therefore, one of the possible answer is possible

Length = $4 k$ and Breadth = $(3 y + 5)$ and Height = $(y - 1)$ .

Class 9 Maths NCERT Chapter 2: Extra Question

Question: Find the value of $k$ if $x - 2$ is a factor of the polynomial $p (x) = x^{3} - 4 x^{2} + k x + 8$ .

Answer:

Since $x - 2$ is a factor of $p (x)$ , by the Factor Theorem:

Therefore, $p (2) = 0$

Substitute $x = 2$ into $p (x)$ :

$p (2) = (2)^{3} - 4 (2)^{2} + 2 k + 8 = 8 - 16 + 2 k + 8 = 0$

$0 = 0 + 2 k \Rightarrow 2 k = 0 \Rightarrow k = 0$

Approach to Solve Questions of Polynomials Class 9

1. Understand the definition and types of polynomials: To start effective classification of polynomials, you must first understand their definitions, along with their degrees and coefficients and linear, quadratic, and cubic types.

2. Learn how to evaluate polynomials: The substitution of values within polynomial expressions helps users evaluate their outcomes, which remains a necessary skill for tackling intricacies in problem-solving.

3. Use the Remainder Theorem: The Remainder Theorem helps determine the remainder outcome when dividing a given polynomial using a linear expression in the form x−a.

4. Master the Factor Theorem: The Factor Theorem allows users to determine linear binomials within polynomials while teaching methods to identify unknown values.

5. Perform algebraic factorisation: Students need to relate to polynomial factorisation through common algebraic patterns with strategies including the middle term separation and grouping techniques.

6. Identify and classify zeroes of polynomials: Study the methods to locate polynomial zeroes while understanding these values in connection to factors and graphical analysis.

Polynomials Class 9 Solutions - Exercise Wise

Students can practice Class 9 Maths Chapter 2 question answers using the exercise link given below.

NCERT Solutions For Class 9 Maths - Chapter Wise

NCERT Solutions for Class 9 Mathematics Chapter 1: Number Systems

NCERT Solutions for Class 9 Mathematics Chapter 2: Polynomials

NCERT Solutions for Class 9 Mathematics Chapter 3: Coordinate Geometry

NCERT Solutions for Class 9 Mathematics Chapter 4: Linear Equations in Two Variables

NCERT Solutions for Class 9 Mathematics Chapter 5: Introduction to Euclid’s Geometry

NCERT Solutions for Class 9 Mathematics Chapter 6: Lines and Angles

NCERT Solutions for Class 9 Mathematics Chapter 7: Triangles

NCERT Solutions for Class 9 Mathematics Chapter 8: Quadrilaterals

NCERT Solutions for Class 9 Mathematics Chapter 9: Circles

NCERT Solutions for Class 9 Mathematics Chapter 10: Heron's Formula

NCERT Solutions for Class 9 Mathematics Chapter 11: Surface Areas and Volumes

NCERT Solutions for Class 9 Mathematics Chapter 12: Statistics

NEET/JEE Offline Coaching

Get up to 90% Scholarship on your NEET/JEE preparation from India’s Leading Coaching Institutes like Aakash, ALLEN, Sri Chaitanya & Others.

Apply Now

NCERT Solutions For Class 9 - Subject Wise

Here are the subject-wise links for the NCERT solutions of class 9:

NCERT Class 9 Books and Syllabus

Given below are some useful links for NCERT books and the NCERT syllabus for class 9:

Keep Working Hard and Happy Learning!

Frequently Asked Questions (FAQs)

1. What are the important topics in NCERT Class 9 syllabus chapter Polynomials ?

The NCERT class 9 maths chapter 2 includes topics such as definition of a polynomial, zeroes, coefficient, degrees, and terms of a polynomial, different types of a polynomial, remainder and factor theorems, and the factorization of polynomials. students should practice these NCERT solutions to get indepth understanding of these concepts which ultimately lead to score well in the exam.

2. What is the number of exercises included in NCERT Solutions for class 9 maths polynomials?

Maths chapter 2 includes five exercises covering topics such as Polynomials in one variable, Zeros of a Polynomial, Real Numbers and their Decimal Expansions, Representing Real Numbers on the Number Line, Operations on Real Numbers, and Laws of Exponents for Real Numbers. Practicing these exercises of NCERT maths class 9 chapter 2 is crucial for achieving a better understanding of the concepts and scoring well in Mathematics. To help students gain confidence, Careers360 experts have designed these solutions to provide comprehensive explanations of the concepts covered in this chapter.

3. What are the advantages of choosing NCERT Solutions for Class 9 Maths Chapter 2?

NCERT Solutions for Class 9 Maths Chapter 2 use straightforward language to explain the concepts, making it accessible even for students who struggle with Mathematics. These solutions are meticulously crafted by a team of experts at Careers360 with the objective of helping students prepare for their CBSE exams effectively.

4. Is it challenging to grasp the concepts in NCERT Solutions for polynomials class 9 solutions?

Regular practice with NCERT Solutions for Class 9 Maths Chapter 2 can enable students to excel in their CBSE exams. These solutions are created by a team of skilled Maths experts at Careers360, and by solving all the questions and comparing their answers with the solutions, students can aim for high scores in their exams.

5. Where can I find the complete solutions of NCERT for Class 9 Maths ?

Here, students can get detailed NCERT solutions for Class 9 Maths which includes solutions to all the exercise of each chapters.

Also Read

NCERT Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.1 - Statistics

NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.4 - Surface Area and Volumes

NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.3- Surface Area and Volumes

NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2 - Surface Area and Volumes

NCERT Class 9 Science Notes - Download Chapter-wise PDFs

NCERT Class 9 Notes - Download Subject Wise PDF Notes

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

Triangles Class 9th Notes - Free NCERT Class 9th Maths Chapter 7 Notes - Download PDF

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Maths Solutions Chapter 2 Polynomials

NCERT Exemplar Class 9 Maths Solutions Chapter 6 Lines and Angles

NCERT Exemplar Class 9 Maths Solutions Chapter 5 Introduction to Euclids Geometry

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Books for Class 9 Maths 2025-26; Download Free PDF

NCERT Books for Class 9 All Subjects - Download Free PDF

NCERT Books for Class 9 Social Science 2025-26: Download PDF

NCERT Books for Class 9 Hindi 2025-26: Download PDF

NCERT Books for Class 9 English 2025-26: Download All Chapters PDF

NCERT Books for Class 9 Science 2025-26; Download PDF (All Chapters)

Articles

SoSE Delhi School Admission Eligibility Criteria 2025: Requirements & Guidelines

May 10, 2025

SoSE Delhi School Admission 2025: All You Need to Know About Eligibility, Dates & Process

May 10, 2025

BHU SET Answer Key 2025: Download Solutions for Class 6, 9, and 11 Entrance Exam

May 09, 2025

BHU School Entrance Test Admit Card 2025 - Download Class 9, 11 SET Admit Card @ bhuonline.in

May 09, 2025

Medical Diploma Courses After 12th - Eligibility Criteria & Top Institutes

May 09, 2025

UPTAC Counselling 2025: Date, Registration, Seat Allotment, Choice Filling, Document Verification

May 08, 2025

NSSNET Admit Card 2025 Out, Navyug School Entrance NTA Hall ticket

May 05, 2025

Home Science Courses After 12th - Eligibility, Duration, Institutes

May 05, 2025

Upcoming School Exams

Assam High School Leaving Certificate Examination

Application Date:01 April,2025 - 15 May,2025

Mock Test

Result

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:02 April,2025 - 19 May,2025

Result

Application Process

Exam Pattern

National Institute of Open Schooling 12th Examination

Admit Card Date:02 April,2025 - 19 May,2025

Application Process

Exam Pattern

Admit Card

Goa Board Higher Secondary School Certificate Examination

Admit Card Date:17 April,2025 - 17 May,2025

Mock Test

Result

Admit Card

Andhra Pradesh Board of Intermediate Education Examination

Admit Card Date:06 May,2025 - 20 May,2025

Result

Admit Card

Mock Test

View All School Exams

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Top Schools

Products & Resources

NCERT Study Material

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

Polynomials Class 9 Questions And Answers PDF Free Download

Polynomials Class 9 Solutions - Important Formulae

NCERT Solutions for Class 9 Maths Chapter 2: Exercise Questions

Class 9 Maths NCERT Chapter 2: Extra Question

Approach to Solve Questions of Polynomials Class 9

Polynomials Class 9 Solutions - Exercise Wise

NCERT Solutions For Class 9 Maths - Chapter Wise

NCERT Solutions For Class 9 - Subject Wise

NCERT Class 9 Books and Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Assam High School Leaving Certificate Examination

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

Goa Board Higher Secondary School Certificate Examination