Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 2.3 Class 9 Maths Chapter 2 - Polynomials

NCERT Solutions for Exercise 2.3 Class 9 Maths Chapter 2 - Polynomials

Edited By Vishal kumar | Updated on Oct 03, 2023 02:08 PM IST

NCERT Solutions for Class 9 Maths Chapter 2: Polynomials Exercise 2.3- Download Free PDF

NCERT solutions for exercise 2.3 class 9 maths chapter 2 Polynomials: An equation formed with variables, exponents, and coefficients together with operations and an equal sign is called a polynomial equation. Here In this exercise 2.3, we will look at polynomial division. The Class 9 Maths chapter 2 exercise 2.3 lists a few practice problems on polynomials that involve the factorization of higher-degree Polynomials with linear polynomials. The Class 9 Maths chapter 2 exercise 2.3 covers the topics like remainder theorem with examples. The concept of division of polynomials with linear polynomial expression over quadratic and cubic degrees will also be discussed in NCERT solutions for Class 9 Maths chapter 2 exercise 2.3.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 2: Polynomials Exercise 2.3- Download Free PDF
  2. Access Polynomials Class 9 Chapter 2 Exercise: 2.3
  3. More About NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3
  4. Benefits of NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3
  5. key Features of Exercise 2.3 Class 9 Maths
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 2.3 Class 9 Maths Chapter 2 - Polynomials
NCERT Solutions for Exercise 2.3 Class 9 Maths Chapter 2 - Polynomials

This 9th class maths exercise 2.3 answers of NCERT Solution set comprises three questions, each with multiple parts, meticulously created by subject experts. The solutions are provided in a detailed, step-by-step format. Additionally, PDF versions of these class 9 maths chapter 2 exercise 2.3 solutions are available for convenient access and offline use. These resources are made accessible to students at no cost. Along with Class 9 Maths Chapter 1 Exercise 2.3 the following exercises are also present.

NCERT Solutions for Class 9 Maths Chapter 2 – Polynomials Exercise 2.3

Download PDF


Access Polynomials Class 9 Chapter 2 Exercise: 2.3

Q1 (i) Find the remainder when x^3 + 3x^2 +3x + 1 is divided by x + 1

Answer:

When we divide x^3 + 3x^2 +3x + 1 by x + 1 .

By long division method, we will get

1639996048817
Therefore, remainder is 0 .

Q1 (ii) Find the remainder when x^3 + 3x^2 +3x + 1 is divided by x - \frac{1}{2}

Answer:

When we divide x^3 + 3x^2 +3x + 1 by x - \frac{1}{2} .

By long division method, we will get

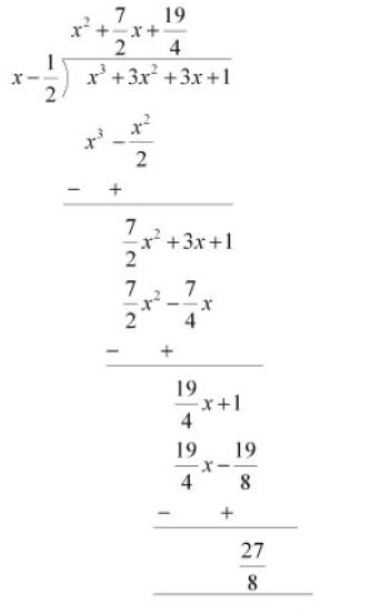1639996081431 Therefore, the remainder is \frac{27}{8}

Q1 (iii) Find the remainder when x^3 + 3x^2 +3x + 1 is divided by x

Answer:

When we divide x^3 + 3x^2 +3x + 1 by x .

By long division method, we will get

1639996102222
Therefore, remainder is 1 .

Q1 (iv) Find the remainder when x^3 + 3x^2 +3x + 1 is divided by x + \pi

Answer:

When we divide x^3 + 3x^2 +3x + 1 by x + \pi .

By long division method, we will get

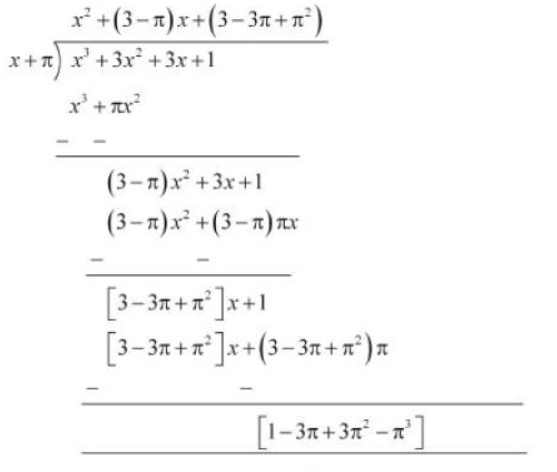
1639996129502
Therefore, the remainder is 1-3\pi + 3\pi^2-\pi^3

Q1 (v) Find the remainder when x^ 3 + 3x^ 2 + 3x + 1 is divided by 5+2x

Answer:

When we divide x^3 + 3x^2 +3x + 1 by 5+2x .

By long division method, we will get

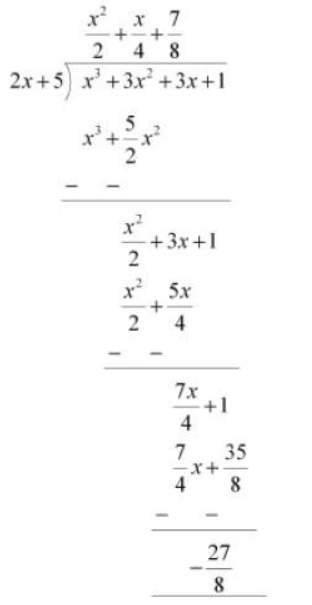
1639996167148
Therefore, the remainder is -\frac{27}{8}


Q2 Find the remainder when x^3 - ax^2 + 6x - a is divided by x - a .

Answer:

When we divide x^3 - ax^2 + 6x - a by x - a .

By long division method, we will get

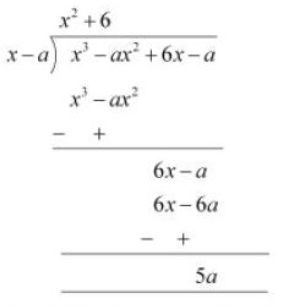
1639996211310
Therefore, remainder is 5a

Q3 Check whether 7 + 3x is a factor of 3x^3 + 7x.

Answer:

When we divide 3x^3 + 7x by 7 + 3x .

We can also write 3x^3 + 7x as 3x^3 +0x^2+ 7x

By long division method, we will get

1639996248244
Since, remainder is not equal to 0

Therefore, 7 + 3x is not a factor of 3x^3 + 7x

More About NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3

There are a variety of questions starting from basic ones to advanced level exam pattern questions covered in NCERT solutions for Class 9 Maths chapter 2 exercise 2.3. The topics like remainder theorem, initiating the concept of algebraic division of polynomials, etc. Solutions of all the numerical questions of Class 9 Maths chapter 2 exercise, 2.3 with specified and student-friendly solutions are available in NCERT solutions for Class 9 Maths chapter 2 exercise 2.3. The basic idea of NCERT Class 9 Maths chapter 2 exercise 2.3 is to simplify mathematics for students, keeping this thing in mind the designing of NCERT solutions for Class 9 Maths chapter 2 exercise 2.3 is done.

Also Read| Polynomials Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3

  • No. 1 benefit of solving exercise 2.3 Class 9 Maths is that the it give an idea to students how the questions can be solved.

  • The second most important benefit of this exercise 2.3 Class 9 Maths is that it acts as a base for the concept flow to exercise 2.4.

key Features of Exercise 2.3 Class 9 Maths

  1. Comprehensive Exercise: 9th class maths exercise 2.3 answers is a comprehensive exercise that covers various topics related to polynomials.

  2. Polynomial Division: This exercise 2.3 class 9 maths focuses on polynomial division, including both long division and synthetic division methods.

  3. Divisor Polynomials: Students learn how to divide polynomials by divisor polynomials of different degrees.

  4. Diverse Problem Set: Class 9 maths ex 2.3 offers a variety of problems with different levels of complexity, allowing students to enhance their skills in polynomial division.
  5. Expert-Created Solutions: Class 9 ex 2.3 solution to the problems are typically provided in the exercise. These solutions are crafted by subject matter experts to ensure accuracy and clarity.
  6. PDF Availability: Students can often download a PDF version of the solutions,

Also see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. Define Remainder Theorem?

The Remainder Theorem is a polynomial division technique based on Euclidean geometry. If we divide a polynomial P(x) by a factor (x – a), which isn't fundamentally an element of the polynomial, we get a smaller polynomial and a remainder polynomial, according to this theorem.

2. How many Questions are there in Chapter 2 exercise 2.3?

There are a total of 3 Questions that contain more than 7 practice problems to do.

3. Why Chapter 2 is Important?

Well if we talk about chapter 2 precisely then its upper variation will be covered in Class 10 where we will learn similar things with polynomials 2 and more variables 

4. Can you divide quadratic with linear?

Since dividing quadratic is possible with linear polynomial because prior polynomial is of higher degree than the succeeding polynomial. Hence it is Possible

5. What is the degree of polynomial x^2 + (x^3 + 1)^2?

The highest power of given expression is x^6 

Therefore degree of the polynomial is 6

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Madhya Pradesh Board 10th Examination

Application Date:01 May,2024 - 20 May,2024

Madhya Pradesh Board 12th Examination

Application Date:01 May,2024 - 20 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

ALLEN Digital Scholarship Admission Test (ADSAT)
ALLEN Digital Scholarship Admission Test (ADSAT)
Apply

Register FREE for ALLEN Digital Scholarship Admission Test (ADSAT)

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top