NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

Class 9 Chapter 5 Introduction to Euclid’s Geometry Notes PDF – Download Free Study Material

Careers360 brings you NCERT Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry notes, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.

Download PDF

NCERT Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry Notes

These NCERT notes for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry have been prepared by Careers360 experts to make learning simpler and to help you score better in exams.

Euclid's Geometry

Euclid’s Geometry, as its name suggests, is a branch of mathematics that is defined by the ancient Greek mathematician Euclid. Geometry is the combination of two Greek words, Geo and Metrein, where Geo means Earth and Metrein means to measure. Euclid is the mathematician from Alexandria, Egypt, who collected all his treatises, also called the Elements, and these elements are divided into thirteen chapters, and each chapter is called a book, which helps to understand geometry. Euclid's geometry is based on a set of axioms and theorems. He defined the notion of points, lines, surfaces, etc.

Surface: Every solid object has its shape and size, and these objects can move from one place to another. These solid shape has their boundaries, and these boundaries are called their surface.

Points: The boundaries of the shape can be curved in the form of straight lines, and these lines end points are called points.

Important Points of Euclid's Book

Euclid defines 23 definitions in his book, and some of the important definitions are given below:
1. The end of the line is always a point.
2. A point can not have its parts like breath, length or width.
3. The length of the line is endless.
4. A line which lies evenly with the points on itself is called a straight line.
5. A surface can have length and breadth only.
6. Lines are the edges of the surface.
7. A surface which lies evenly with the straight lines on itself is called a plane surface.

Euclid’s Postulates

Certain properties were not proved but assumed as these are universal truths, and Euclid divided these truths into two categories.
1. Postulate for assumption
2. Axioms for notions

Euclid defined five postulates, and these are:

1. A straight line may be drawn from any one point to any other point.

Example: A line can be drawn by joining the endpoints on the paper or any surface.

2. A terminated line can be produced indefinitely.

Example: A Railway track that can be further added for a new city or village station.

3. A circle can be drawn with any centre and any radius.

Example: Using a compass, you can draw a circle with any centre or radius.

4. All right angles are equal to one another.

Example: Right angles mean the angle is 90 degrees, so all the angles are equal.

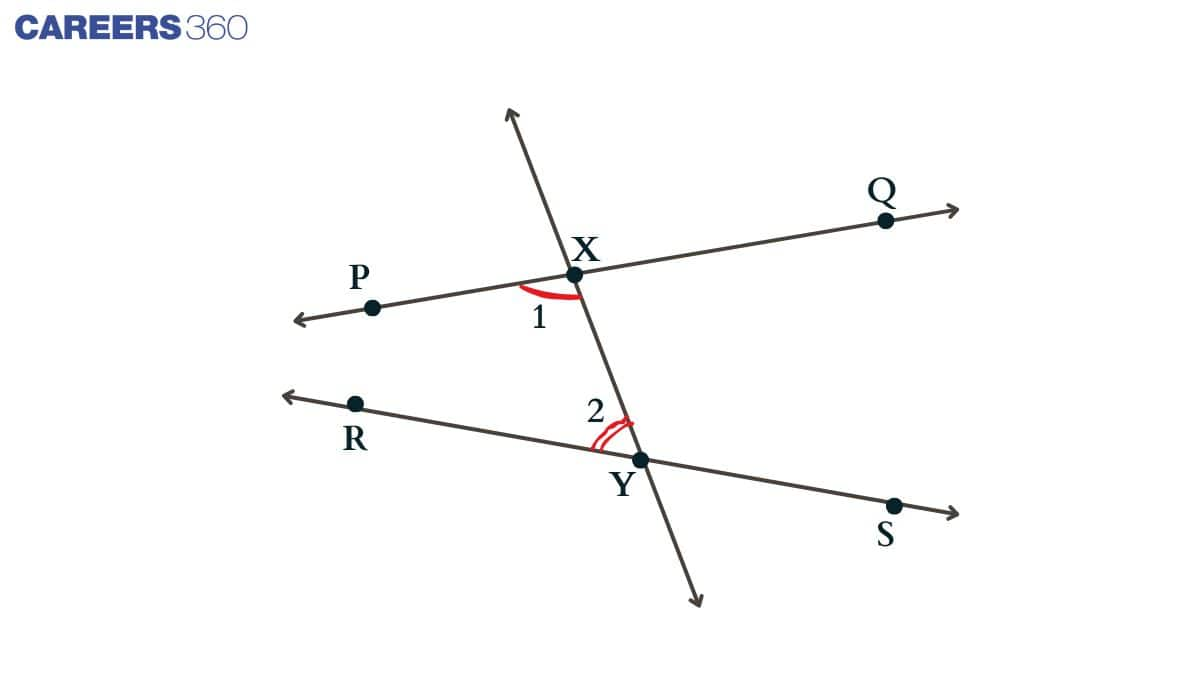
5. If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Example: The line XY passes through the lines PQ and RS such that the sum of the interior angles 1 and 2 is less than 180° on the left side of XY. Therefore, the lines AB and CD will eventually intersect on the left side of XY.

Euclid’s Axioms

Euclid's seven axioms are given below:

1. Things which are equal to the same thing are equal to one another.

Example: Suppose you and your cousin were born on the same date, same month and same year, then both of you are of equal age.

2. If equals are added to equals, the wholes are equal.

Example: Suppose you and your friend have 2 kg of milk each, and after pouring these 2 kg of milk from each, it becomes 4kg of milk.

3. If equals are subtracted from equals, the remainders are equal.

Example: Suppose you and your brother have 10 chocolates and both eat 2 chocolates, then both have 8-8 chocolates each.

4. Things which coincide with one another are equal to one another.

Example: Suppose two bowls fit with each other, then these two bowls are equal to each other. Therefore, we can say that they are coinciding.

5. The whole is greater than the part.

Example: Suppose we have a chapati, then part of the chapati is always less the the whole.

6. Things which are double of the same things are equal to one another.

Example: Suppose Ram has double balls, then Piyush and Shyam have double balls, then Piyush, then Ram and Shyam both have an equal number of balls.

7. Things which are halves of the same things are equal to one another.

Example: Suppose Ram has half of the balls, then Piyush and Shyam have half of the balls, then Piyush, it implies that Ram and Shyam both have an equal number of balls.

Theorem

Two distinct lines can not have more than one point in common.

Proof: Suppose there are two lines, ‘P’ and ‘Q’, that have one common point.
Now, let us assume that ‘P' and ‘Q’ have two common points, named X and Y. Therefore, these two lines, P and Q, pass through two distinct points X and Y. But this assumption contradicts the assumption that only one line can pass through two distinct points. Therefore, the assumption we made is wrong, and the two lines ‘P' and ‘Q’ have only one common point.

Equivalent Versions of Euclid’s Fifth Postulate

(i) For every line l and every point P not lying on l, there exists a unique line ‘m’ passing through P and parallel to l’.
(ii) Two distinct intersecting lines cannot be parallel to the same line.

How to Use the Introduction to Euclid’s Geometry Class 9 Notes Effectively?

Euclid’s Geometry becomes easy to understand when we understand the basic ideas of points, lines, and the rules that define them. This chapter is mostly about learning Euclid’s definitions, axioms, and postulates in a simple way. Reading them efficiently helps us understand how all geometry starts, and the Class 9 Maths chapter 5 notes make this easier for us. Here are some more points on how these notes are important.

• Read each definition, axiom, and postulate carefully and try to relate them to simple shapes around us so they feel easy to understand.
• Make short summaries of the important axioms and keep them for quick revision before attempting any question.
• Use the NCERT Class 9 Maths chapter 5 notes while practising textbook questions to understand how these rules are applied.
• Follow the NCERT Class 9 Maths chapter 5 notes to build a strong base, because these ideas help us later in higher classes when geometry becomes more detailed.

NCERT Notes for Class 9 Chapter Wise

We at Careers360 compiled all the NCERT class 9 Maths notes in one place for easy student reference. The following links will allow you to access them.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 9 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

Before the start of a new academic year, students should refer to the latest syllabus to determine the chapters they’ll be studying. Below are the updated syllabus links, along with some recommended reference books.

• NCERT Books Class 9 Maths
• NCERT Syllabus Class 9 Maths
• NCERT Books Class 9
• NCERT Syllabus Class 9
• NCERT Books for Class 9 Science