NCERT Solutions for Exercise 2.4 Class 9 Maths Chapter 2 - Polynomials

Q1 (i) Determine which of the following polynomials has $(x+1)$ a factor : $x^3+x^2+x+1$

Answer:

Let p(x) = x³ + x² + x +1

Use the Factor Theorem, which says:

If p(–1) = 0, then (x + 1) is a factor of the polynomial p(x).

So, p(−1) = (−1)³ + (−1)² + (−1) + 1 = -1 + 1 - 1 + 1 = 0

Therefore, Yes, (x + 1) is a factor of polynomial $p(x)=x^3+x^2+x+1$

Q1 (ii) Determine which of the following polynomials has $(x+1)$ a factor : $x^4+x^3+x^2+x+1$

Answer:

Let p(x) = x⁴ + x³ + x² + x + 1

Use the Factor Theorem, which says:

If p(–1) = 0, then (x + 1) is a factor of the polynomial p(x).

So, p(−1) = (−1)⁴ + (−1)³ + (−1)² + (−1) + 1 = 1 - 1 + 1 - 1 + 1 = 1

Therefore, No, (x + 1) is not a factor of polynomial $p(x)=x^4+x^3+x^2+x+1$

Q1 (iii) Determine which of the following polynomials has $(x+1)$ a factor : $x^4+3x^3+3x^2+x+1$

Answer:

Let p(x)= x⁴ + 3x³ + 3x² + x + 1

Use the Factor Theorem, which says:

If p(–1) = 0, then (x + 1) is a factor of the polynomial p(x).

So, p(−1) = (−1)⁴ + 3(−1)³ + 3(−1)² + (−1) + 1 = 1 - 3 + 3 - 1 + 1 = 1

Therefore, No, (x + 1) is not a factor of polynomial $p(x)=x^4+3x^3+3x^2+x+1$

Q1 (iv) Determine which of the following polynomials has $(x+1)$ a factor : $x^3-x^2-(2+\sqrt{2})x+\sqrt{2}$

Answer:

Let p(x) = $x^3-x^2-(2+\sqrt{2})x+\sqrt{2}$

Use the Factor Theorem, which says:

If p(–1) = 0, then (x + 1) is a factor of the polynomial p(x).

So, $p(-1)=(-1{)}^3-(-1{)}^2-(2+\sqrt{2})(-1)+\sqrt{2}$ = $-1-1+2+\sqrt{2}+\sqrt{2}$ = $2\sqrt{2}\ne 0$

Therefore, No, (x + 1) is not a factor of polynomial p(x) = $x^3-x^2-(2+\sqrt{2})x+\sqrt{2}$

Q2 (i) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x)=2x^3+x^2-2x-1,g(x)=x+1$

Answer:

g(x) = 0

⇒ x + 1 = 0

⇒ x = −1

Now, p(−1) = 2(−1)³ + (−1)² – 2(−1) –1 = −2 + 1 + 2 −1 = 0

Therefore, Yes, g(x) is a factor of p(x)

Q2 (ii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x)=x^3+3x^2+3x+1,g(x)=x+2$

Answer:

g(x) = 0

⇒ x + 2 = 0

⇒ x = −2

Now,

p(−2) = (−2)³ + 3(−2)² + 3(−2) + 1

= − 8 + 12 − 6 + 1

= −1 ≠ 0

Therefore, No, g(x) is not a factor of p(x)

Q2 (iii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x)=x^3-4x^2+x+6,g(x)=x-3$

Answer:

g(x) = 0

⇒ x − 3 = 0

⇒ x = 3

Now,

p(3) = (3)³ − 4(3)² + (3) + 6

= 27 − 36 + 3 + 6

= 0

Therefore, yes, g(x) is a factor of p(x).

Q3 (i) Find the value of k , if $x-1$ is a factor of p(x) in the following case: $p(x)=x^2+x+k$

Answer:

As (x - 1) is a factor of p(x), it means that p(1) = 0

So, By the Factor Theorem

⇒ (1)² + (1) + k = 0

⇒ 1 + 1 + k = 0

⇒ 2 + k = 0

⇒ k = −2

Q3 (ii) Find the value of k , if $x-1$ is a factor of p(x) in the following case: $p(x)=2x^2+kx+\sqrt{2}$

Answer:

As (x - 1) is a factor of p(x), it means that p(1) = 0

So, by the factor theorem

⇒ $2(1{)}^2+k(1)+\sqrt{2}$ = 0

⇒ $2+k+\sqrt{2}$ = 0

⇒ k = $-2-\sqrt{2}$

Q3 (iii) Find the value of k , if $x-1$ is a factor of p(x) in the following case: $p(x)=k{x}^2-\sqrt{2}x+1$

Answer:

As (x - 1) is a factor of p(x), it means that p(1) = 0

So, by the factor theorem

⇒ $k(1{)}^2-\sqrt{2}(1)+1$ = 0

⇒ k = $-1+\sqrt{2}$

Q3 (iv) the value of k , if $x-1$ is a factor of p(x) in the following case: $p(x)=k{x}^2-3x+k$

Answer:

As (x - 1) is a factor of p(x), it means that p(1) = 0

So, by the factor theorem

⇒ $k(1)^2 -3 (1) + k$ = 0

⇒ k − 3 + k = 0

⇒ 2k − 3 = 0

⇒ k = $\frac{3}{2}$

Q4 (i) Factorise : $12x^2-7x+1$

Answer:

Given polynomial is $12x^2-7x+1$

We need to factorise the middle term into two terms such that their product is equal to $12\times 1=12$ and their sum is equal to $-7$

We can solve it as

$\Rightarrow 12x^2-7x+1$

$\Rightarrow 12x^2-3x-4x+1$ $(\because -3\times -4=12and-3+(-4)=-7)$

$\Rightarrow 3x(4x-1)-1(4x-1)$

$\Rightarrow (3x-1)(4x-1)$

Q4 (ii) Factorise : $2x^2+7x+3$

Answer:

Given polynomial is $2x^2+7x+3$

We need to factorise the middle term into two terms such that their product is equal to $2\times 3=6$ and their sum is equal to $7$

We can solve it as

$\Rightarrow 12x^2-7x+1$

$\Rightarrow 2x^2+6x+x+3$ $(\because 6\times 1=6and6+1=7)$

$\Rightarrow 2x(x+3)+1(x+3)$

$\Rightarrow (2x+1)(x+3)$

Q4 (iii) Factorise : $6x^2+5x-6$

Answer:

Given polynomial is $6x^2+5x-6$

We need to factorise the middle term into two terms such that their product is equal to $6\times -6=-36$ and their sum is equal to $5$

We can solve it as

$\Rightarrow 6x^2+5x-6$

$\Rightarrow 6x^2+9x-4x-6$ $(\because 9\times -4=-36and9+(-4)=5)$

$\Rightarrow 3x(2x+3)-2(2x+3)$

$\Rightarrow (2x+3)(3x-2)$

Q4 (iv) Factorise : $3x^2-x-4$

Answer:

Given polynomial is $3x^2-x-4$

We need to factorise the middle term into two terms such that their product is equal to $3\times -4=-12$ and their sum is equal to $-1$

We can solve it as

$\Rightarrow 3x^2-x-4$

$\Rightarrow 3x^2-4x+3x-4$ $(\because 3\times -4=-12and3+(-4)=-1)$

$\Rightarrow x(3x-4)+1(3x-4)$

$\Rightarrow (x+1)(3x-4)$

Q5 (i) Factorise : $x^3-2x^2-x+2$

Answer:

Given polynomial is $x^3-2x^2-x+2$

Now, by the hit and trial method, we observed that $(x+1)$ is one of the factors of the given polynomial.

By the long division method, we will get

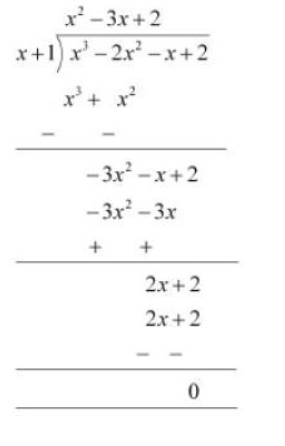We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^3-2x^2-x+2=(x+1)(x^2-3x+2)+0$

$=(x+1)(x^2-2x-x+2)$

$=(x+1)(x-2)(x-1)$

Therefore, on factorization of $x^3-2x^2-x+2$ we will get $(x+1)(x-2)(x-1)$

Q5 (ii) Factorise : $x^3-3x^2-9x-5$

Answer:

Given polynomial is $x^3-3x^2-9x-5$

Now, by the hit and trial method, we observed that $(x+1)$ is one of the factors of the given polynomial.

By the long division method, we will get

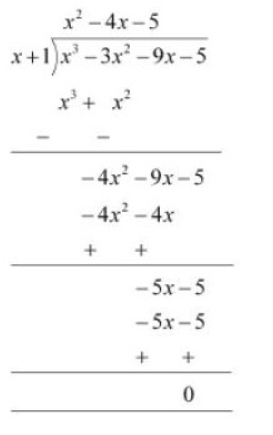We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^3-3x^2-9x-5=(x+1)(x^2-4x-5)$

$=(x+1)(x^2-5x+x-5)$

$=(x+1)(x-5)(x+1)$

Therefore, on factorization of $x^3-3x^2-9x-5$ we will get $(x+1)(x-5)(x+1)$

Q5 (iii) Factorise : $x^3+13x^2+32x+20$

Answer:

Given polynomial is $x^3+13x^2+32x+20$

Now, by the hit and trial method, we observed that $(x+1)$ is one of the factors of the given polynomial.

By the long division method, we will get

We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^3+13x^2+32x+20=(x+1)(x^2+12x+20)$

$=(x+1)(x^2+10x+2x+20)$

$=(x+1)(x+10)(x+2)$

Therefore, on factorization of $x^3+13x^2+32x+20$ we will get $(x+1)(x+10)(x+2)$

Q5 (iv) Factorise : $2y^3+y^2-2y-1$

Answer:

Given polynomial is $2y^3+y^2-2y-1$

Now, by the hit and trial method, we observed that $(y-1)$ is one of the factors of the given polynomial.

By the long division method, we will get

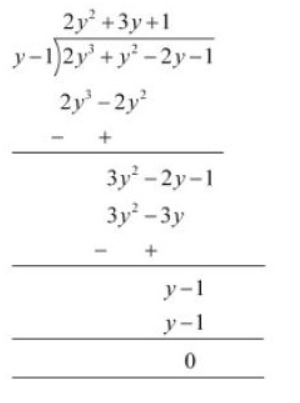We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$2y^3+y^2-2y-1=(y-1)(2y^2+3y+1)$

$=(y-1)(2y^2+2y+y+1)$

$=(y-1)(2y+1)(y+1)$

Therefore, on factorization of $2y^3+y^2-2y-1$ we will get $(y-1)(2y+1)(y+1)$