Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 - Introduction To Euclid's Geometry

NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 - Introduction To Euclid's Geometry

Updated on May 02, 2025 04:56 PM IST

The exercise establishes the fundamental basis of Euclidean geometry through its presentation. This turns toward knowing Euclid's method of constructing logical geometry with his definitions and axioms and postulates. The programmed approach created fundamentals to produce advanced geometrical theorems and constructions by tracing facts down from essential starting points thus establishing the core structure of classical geometry.

This Story also Contains
  1. NCERT Solutions Class 9 Maths Chapter 5: Exercise 5.1
  2. Topics Covered in Chapter 5 – Introduction to Euclid’s Geometry (Exercise 5.1)
  3. NCERT Solutions of Class 10 Subject Wise
  4. Subject-Wise NCERT Exemplar Solutions

Through this exercise students learn to differentiate between axioms and postulates by analyzing their importance as well as their application process for creating mathematical logic systems. Students can better comprehend complex abstract geometrical concepts through these guided NCERT Solutions which function perfectly with regular NCERT Books for constructing a firm foundation in geometry.

NCERT Solutions Class 9 Maths Chapter 5: Exercise 5.1

Q1 Which of the following statements are true and which are false? Give reasons for your answers.

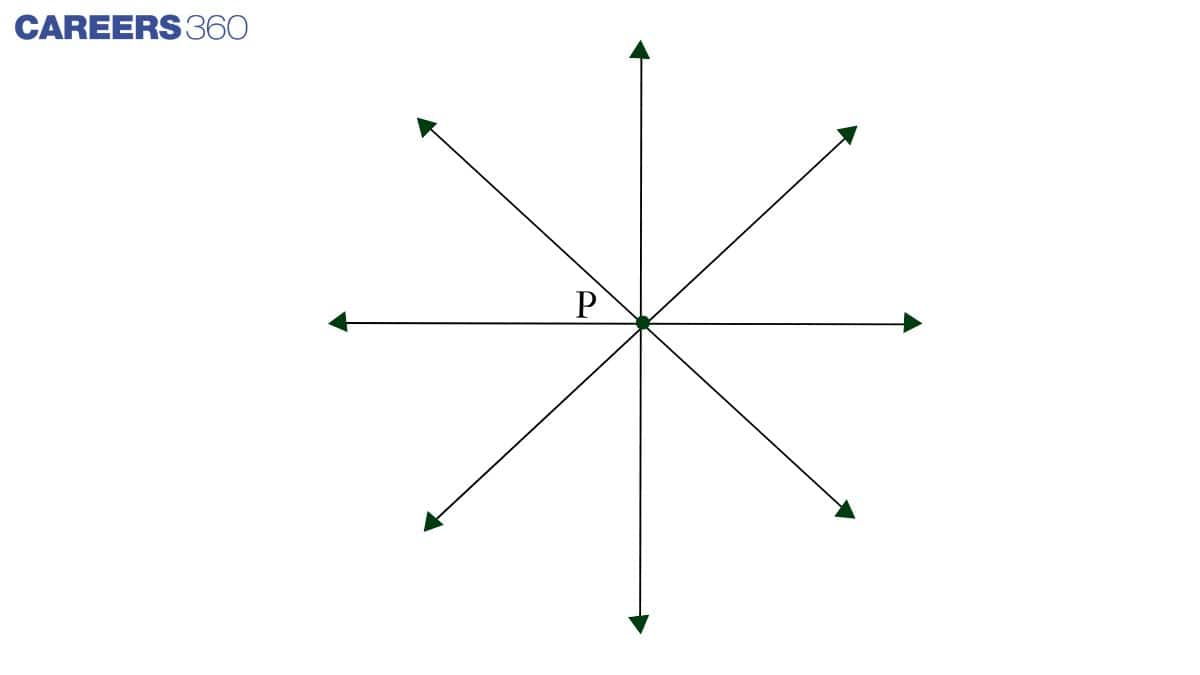
(i) Only one line can pass through a single point.

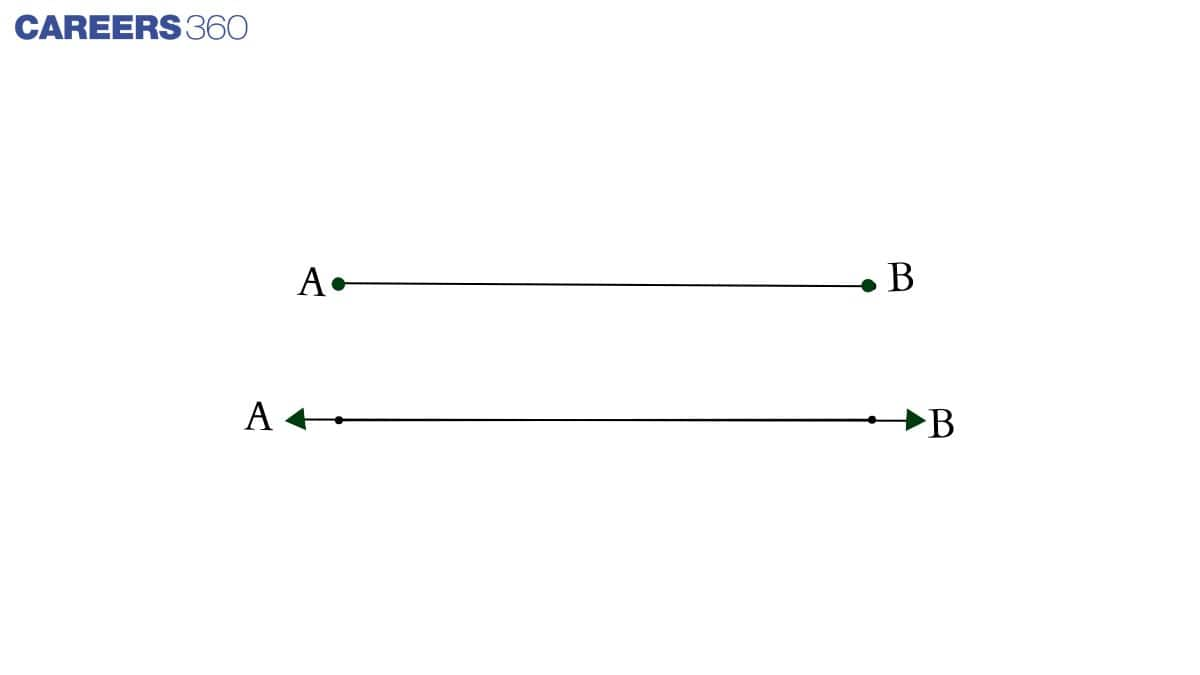
(ii) There are an infinite number of lines which pass through two distinct points.

(iii) A terminated line can be produced indefinitely on both the sides.

(iv) If two circles are equal, then their radii are equal.

(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.

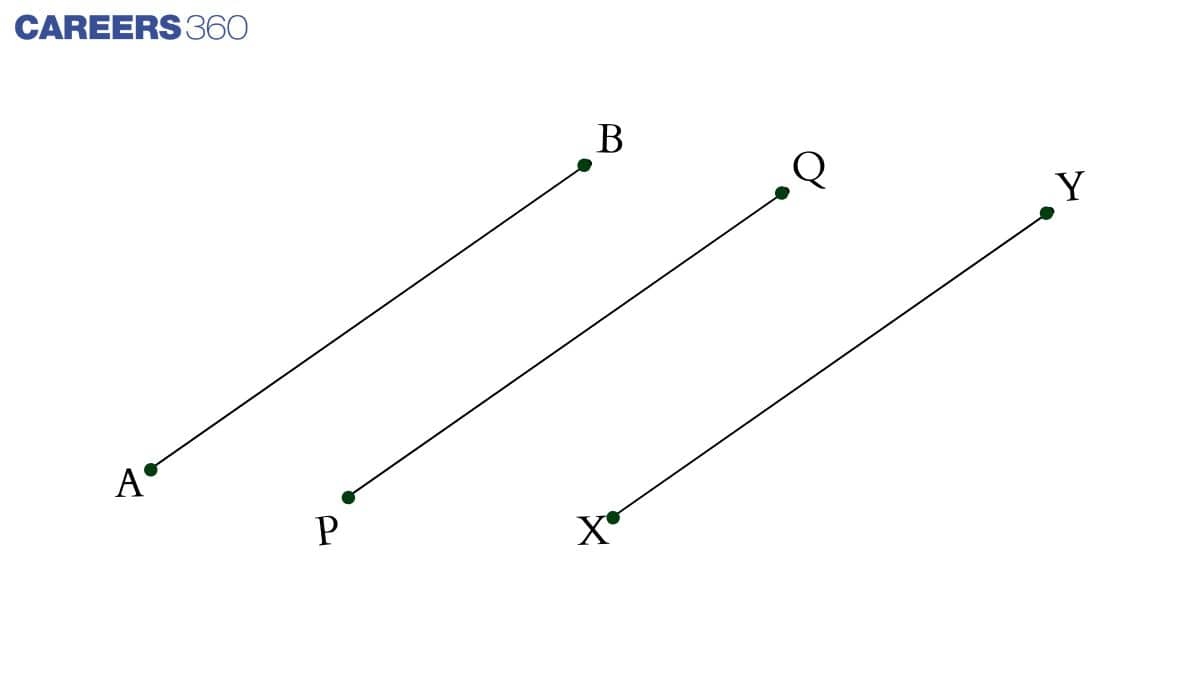
1000005886

Answer:

i) FALSE
Because, the single point allows an infinite number of parallel lines to be drawn through it. As shown in the diagram below
1000005890

ii) FALSE
Because, one line exists between two distinct points because of fundamental mathematical principles. As shown in the diagram below
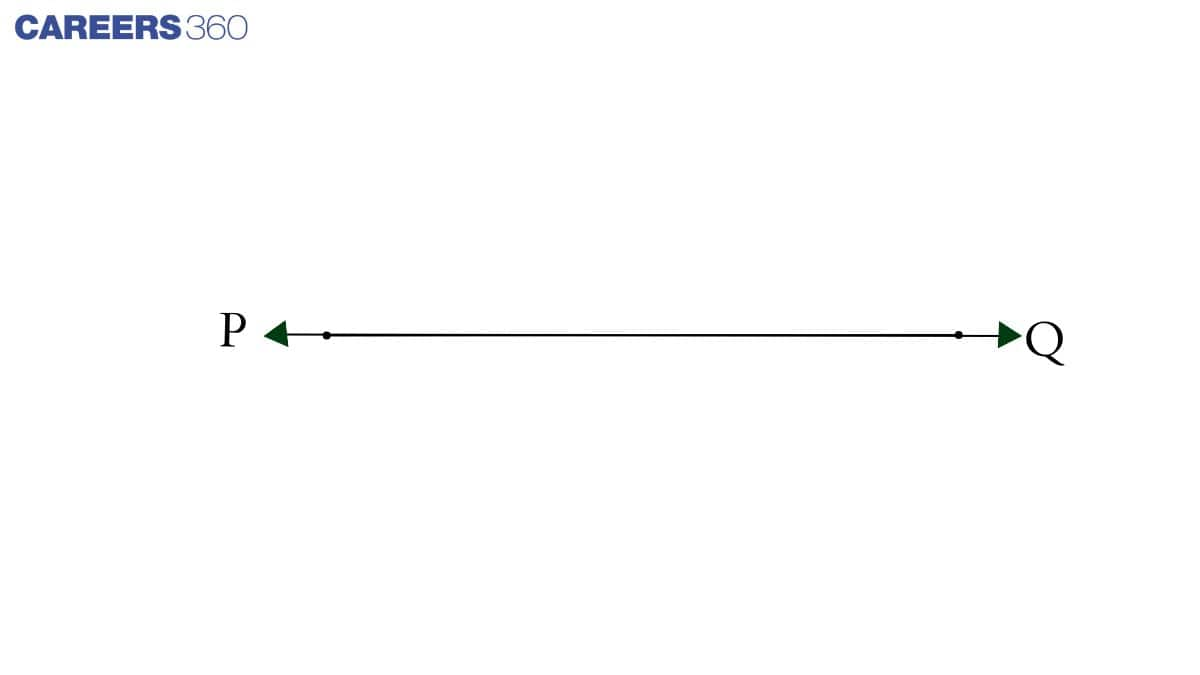
1000005888

iii) TRUE
Because, the production of a terminated line remains possible without limits from both sides. As shown in the diagram below
1000005882

iv) TRUE
Because, when two circles match in size then both their central points together with their outer boundaries align perfectly while their radii become equal with each other.

v) TRUE
By Euclid’s first axiom things which are equal to the same thing, are equal to one another.

Q2 (i) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: An infinite flat two-dimensional surface defines what a plane represents

Point: Points represent small dots which hold no dimensions like length, breadth or height and exist only to indicate position.

Line: The definition of a line describes an infinite straight one-dimensional shape without thickness which continues indefinitely forward and backward.

i) Parallel line:-
if two lines in a plane never cross one another and their perpendicular distance is always constant. Two lines are thus referred to as parallel lines.

Q2 (ii) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? (ii) perpendicular lines

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: An infinite flat two-dimensional surface defines what a plane represents

Point: Points represent small dots which hold no dimensions like length, breadth or height and exist only to indicate position.

Line: The definition of a line describes an infinite straight one-dimensional shape without thickness which continues indefinitely forward and backward.

ii) perpendicular line:-
If two lines intersect with each other and make a right angle at the point of intersection. Then, two lines are called perpendicular lines.

Q2 (iii) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? iii) line segment

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: An infinite flat two-dimensional surface defines what a plane represents

Point: Points represent small dots which hold no dimensions like length, breadth or height and exist only to indicate position.

Line: The definition of a line describes an infinite straight one-dimensional shape without thickness which continues indefinitely forward and backward.

iii) line segment:-
A line segment is a straight line having two end points that have a fixed length and cannot be stretched further.

Q2 (iv) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? iv) radius of circle

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: An infinite flat two-dimensional surface defines what a plane represents

Point: Points represent small dots which hold no dimensions like length, breadth or height and exist only to indicate position.

Line: The definition of a line describes an infinite straight one-dimensional shape without thickness which continues indefinitely forward and backward.

iv) Radius of the circle: -
The radius of a circle is the separation between the circle's center and any point on its circumference.

Q2 (v) Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them? v) square

Answer:

Yes, there are other terms that are needed to be defined first which are:

Plane: An infinite flat two-dimensional surface defines what a plane represents

Point: Points represent small dots which hold no dimensions like length, breadth or height and exist only to indicate position.

Line: The definition of a line describes an infinite straight one-dimensional shape without thickness which continues indefinitely forward and backward.

v) Square:-
Any quadrilateral with equal four sides and right angles at all interior angles is called a square.

Q3 Consider two ‘postulates’ given below:

(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.

(ii) There exist at least three points that are not on the same line.

Do these postulates contain any undefined terms? Are these postulates consistent?

Do they follow from Euclid’s postulates? Explain.

Answer:

The following postulates contain a number of undefined terms:

1) No information regarding the plane is provided, including whether or not the points are in the same plane.

2) A plane has an endless number of points. However, it is unclear from this point C's location whether it is on the line segment that joins AB or not.

Yes, these postulates hold true and consistent in the following two scenarios:

(i) Point C is located on the line segment that connects A and B.

(ii) The line segment connecting A and B does not contain Point C.

No, Euclid's postulates don't support them. They adhere to the principles.

Q4 If a point C lies between two points A and B such that AC = BC, then prove that AC = 1/2 AB. Explain by drawing the figure.

Answer:

Given, AC = BC
Now, draw the figure as below:
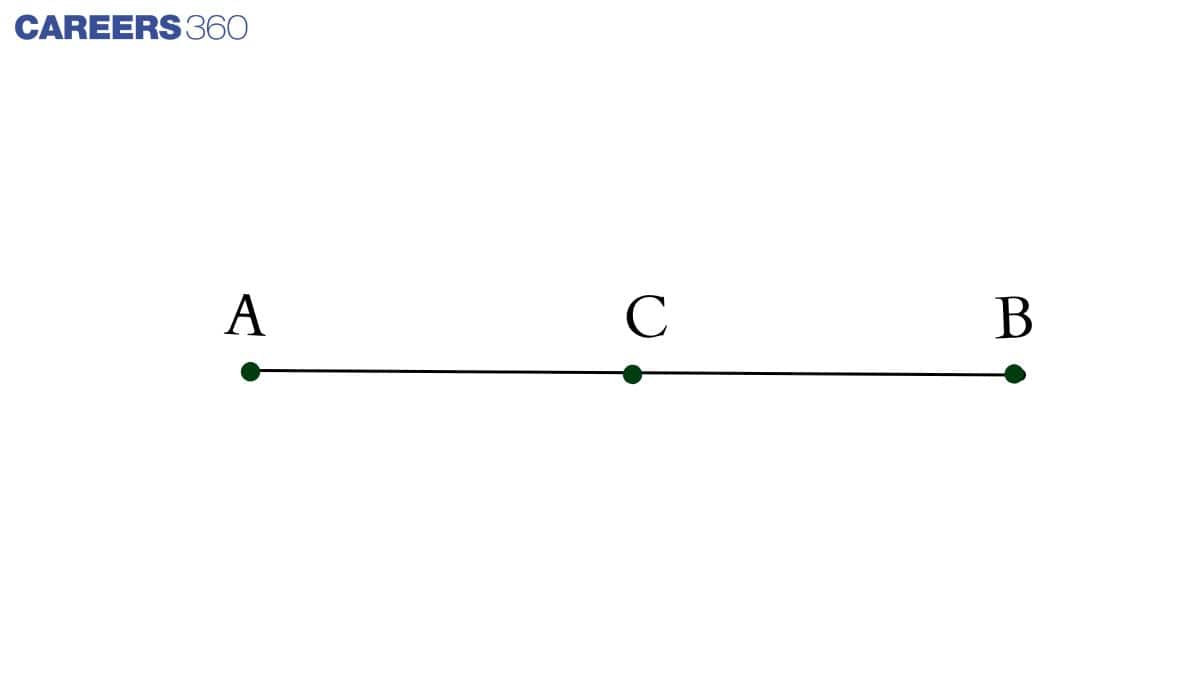
1000005874

In the figure, AB coincides with AC + BC.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. Hence, it is deduced that AC + BC = AB
So from this we can conclude; 2AC = AB (∵AC=BC)
Therefore, AC=12AB
Hence proved.

Q5 In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.

Answer:

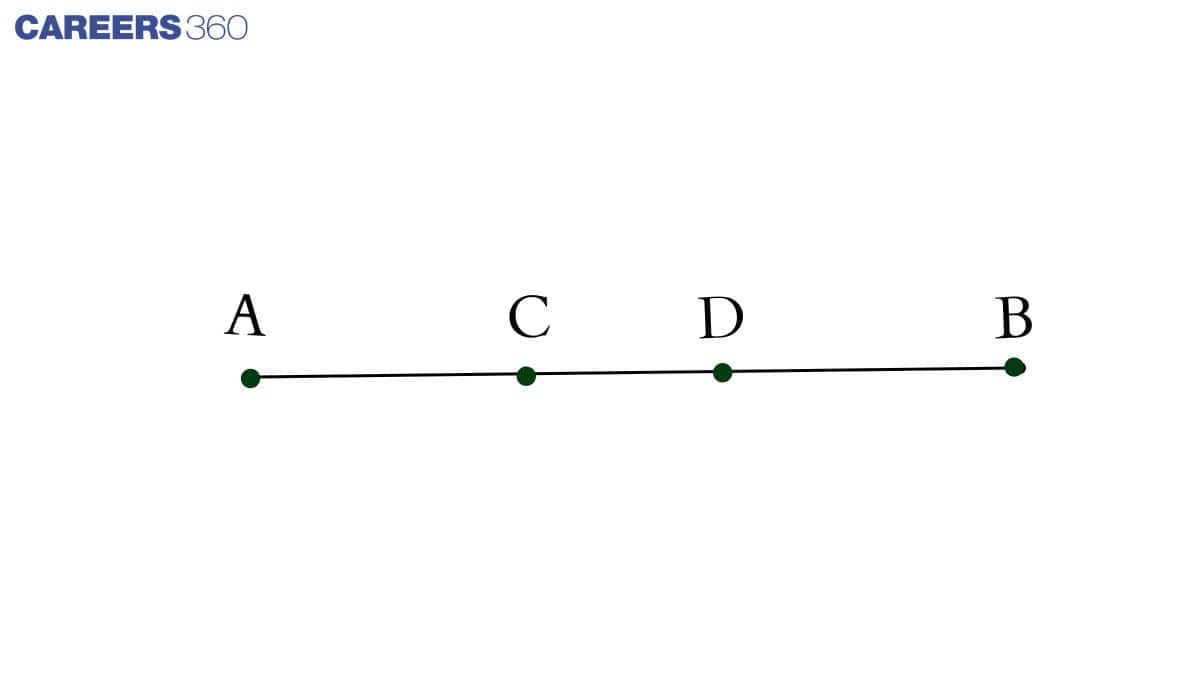
1000005884

Let's consider, there are two midpoints C and D of a line segment A and B.
Now, If C is the midpoint then, AC = BC
And, this concludes, AB coincides with AC + BC.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that AC + BC = AB
Therefore, we can say that
2AC = AB -(i)

Similarly, in case of point D.
If D is the midpoint then, AD = BD
And, when considering the figure we can conclude, AB coincides with AD + BD.
Also, Euclid’s Axiom (4) says that things which coincide with one another are equal to one another. So, it can be deduced that AD + BD = AB
From this, we can say that
2AD = AB -(ii)
Now,
From equation (i) and (ii) we get
AD = AC
and this is only possible when C and D are the same points
Hence, our assumption is wrong and there is only one midpoint of line segment AB.

Q6 In Fig. 5.10, if AC = BD, then prove that AB = CD.

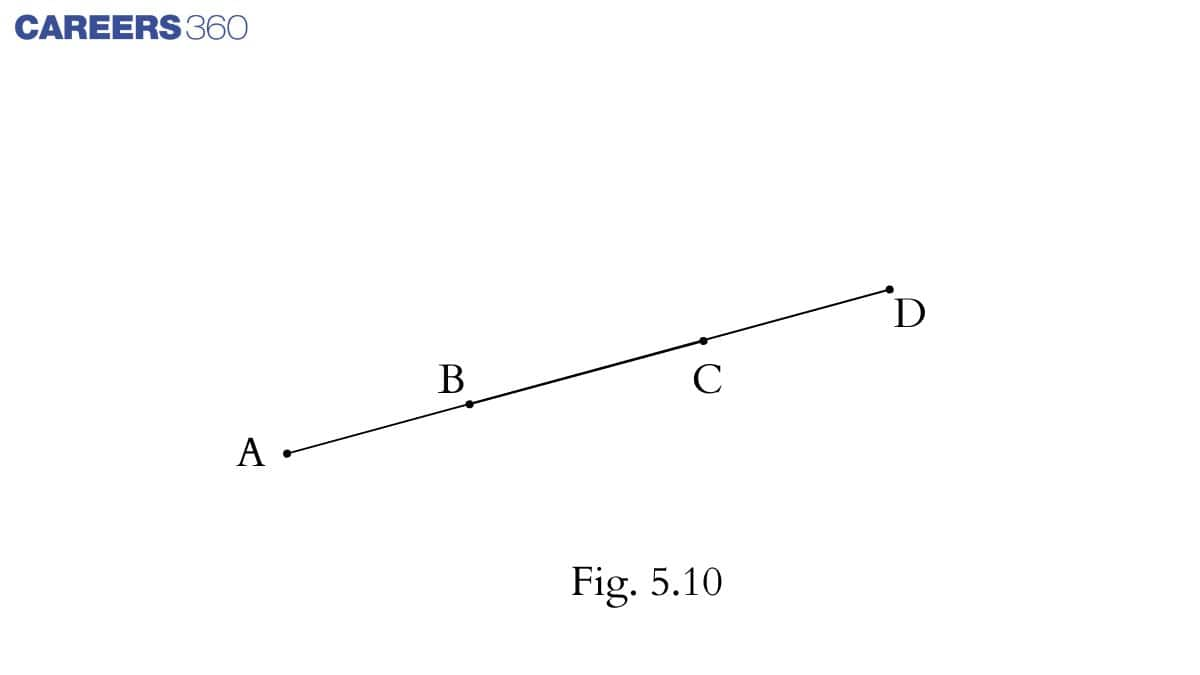
1000005880

Answer:

From the figure given,
We can say, AC = AB + BC and BD = BC + CD
It is given that AC = BD
Therefore, we can write:
AB + BC = BC + CD
Now, According to Euclid's axiom, when equals are subtracted from equals, the remainders are also equal. Subtracting BC from both sides.
We get: AB + BC - BC = BC + CD - BC
AB = CD

Hence proved

Q7 Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)

Answer:

Axiom 5 states that the whole is greater than the part.
Let's Understand with the help of an example:

Let A = x + y + z (where A , x , y , z all are positive numbers)
Now, we can clearly see that A > x , A > y , A > z
Hence, by this we can say that the whole (A) is greater than the parts. (x , y , z)

Other real life examples:

  • If you have a stick and break it into two parts, clearly the original stick (the whole) is longer than either of the parts.
  • In mathematics, if a number is divided into parts (say 10 into 4 and 6), then 10 (the whole) is greater than each part.


Topics Covered in Chapter 5 – Introduction to Euclid’s Geometry (Exercise 5.1)

  • Euclid’s definitions, axioms and postulates: Euclid laid the foundation of geometry using clearly defined terms, universally accepted truths (axioms), and basic assumptions (postulates). These formed the building blocks for all geometrical reasoning.
  • Application of axioms to solve reasoning questions: In geometric proofs, axioms are used to support logical stages. By applying fundamental facts to novel circumstances, this aids pupils in honing their reasoning abilities.
  • Consistency and independence of postulates: Euclid's postulates are independent, meaning no postulate can be inferred from the others, and consistent, meaning they do not contradict one another. This guarantees a solid foundation for geometric reasoning.
  • Basic construction of geometric proofs: At this stage students learn to build arguments by combining definitions with axioms and postulates. Student learning enables them to observe how advanced geometric theorems develop from basic well-defined principles.

Also see-

NEET/JEE Offline Coaching
Get up to 90% Scholarship on your NEET/JEE preparation from India’s Leading Coaching Institutes like Aakash, ALLEN, Sri Chaitanya & Others.
Apply Now

NCERT Solutions of Class 10 Subject Wise

Subject-Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. Define Euclid’s geometry , as per NCERT solutions for Class 9 Maths chapter 5 exercise 5.1 ?

Euclid's geometry is defined as the study of geometry based on undefined notions such as points, lines, and planes of flat spaces, according to NCERT solutions for Class 9 Maths chapter 5 exercise 5.1

2. Who introduced Euclid’s geometry?

Euclid’s geometry was introduced by Euclid. 

3. Euclid is the Father of ______.

Euclid is the Father of Geometry.

4. Define perpendicular lines , According to NCERT solutions for Class 9 Maths chapter 5 exercise 5.1.

The lines that intersect each other in a plane at right angles are said to be perpendicular to each other, according to NCERT solutions for Class 9 Maths chapter 5 exercise 5.1

5. The number of axiom of Euclid’s geometry is ______

The number of axioms of Euclid’s geometry is 7.

6. Rani is of the same age as vani . Sudha is also of the same age as vani . State the correct Euclid’s axiom that illustrates the relative ages of Rani and Sudha

The correct Euclid’s axiom that illustrates the relative ages of Rani and Sudha is the first axiom. According to the first axiom, Things that are equal to the same thing are equal to one another.

7. How many lines can pass through a given point?

There are an endless number of lines that can pass through a given spot.

8. Things that are similar to one another are referred to as _____

Things that are similar to one another are referred to as equal. 

Reason: According to axiom 4, things that are at the same place at the same time are equal.

9. A straight line segment can be drawn for any two given points is stated in the form of _______

A straight line segment can be drawn for any two given points as stated in the form of a postulate

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Admit Card Date:02 April,2025 - 19 May,2025

National Institute of Open Schooling 12th Examination

Admit Card Date:02 April,2025 - 19 May,2025

National Means Cum-Merit Scholarship

Application Date:13 April,2025 - 07 May,2025

Goa Board Higher Secondary School Certificate Examination

Admit Card Date:17 April,2025 - 17 May,2025

Bihar Board 12th Examination

Admit Card Date:20 April,2025 - 13 May,2025

View All School Exams

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Study Resources, Applications and Opportunities

ALLEN Coaching
ALLEN Coaching
Apply

Register for ALLEN Scholarship Test & get up to 90% Scholarship

NEET/JEE Coaching Scholarship
NEET/JEE Coaching Scholarship
Apply

Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes

NEET Most scoring concepts
NEET Most scoring concepts
Get now

This ebook serves as a valuable study guide for NEET 2025 exam.

NEET Previous 10 Year Questions
NEET Previous 10 Year Questions
Get now

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

JEE Main Important Physics formulas
Get now

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Get now

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

View All Application Forms
News and Notifications
Teen becomes first to clear class 10 exams in UP village since independence
Delhi CM meets parents of private school students; assures regulation, transparency in fee fixation
17-year-old gang-rape survivor appears for Class 11 exam in Rajasthan's Jhalawar
West Bengal Governor grants sanction to ED for prosecution of ex-Education Minister Partha Chatterjee
ACB files case against Sisodia, Jain for alleged corruption in classroom construction, AAP slams it as politic
Delhi School Fee Hike: How govt plans to check private schools with new bill and why it’s ‘complicated’
Three madrasa teachers held for assaulting minor students in Gujarat
Back to top