NCERT Exemplar Class 9 Maths Solutions Chapter 12 Herons Formula
Heron’s Formula is a method to calculate the area of a triangle. The only thing required is the measurement of each side of a triangle. This makes it very useful to find the area of a scalene triangle. For example, if a triangle has sides 5 cm, 6 cm, and 7 cm, then instead of using the base and height, we can apply Heron’s formula. You should know the concept of the semi-perimeter of the triangle ie, the semiperimeter is half of the sum of all sides of the triangle. The NCERT Exemplar Class 9 Chapter 12, Heron's Formula, provides you with a good number of questions to understand the concept of Heron's formula. The NCERT exemplar Class 9 Maths chapter 12 solutions are highly accurate and elaborate.
This Story also Contains
- Important Topics for NCERT Exemplar Solutions Class 9 Maths Chapter 12:
- NCERT Exemplar Class 9 Maths Solutions Chapter
- NCERT Class 9 Exemplar Solutions Subject-Wise:
- NCERT Solutions for Class 9 Mathematics: Chapter-wise
- NCERT Class 9 Exemplar Solutions for Other Subjects
- NCERT Solution Subject Wise
At Careers 360, highly skilled subject experts have prepared these NCERT Exemplar Class 9 Maths chapter 12 solutions to develop an organized learning flow for the students practicing the NCERT Class 9 Maths Book. These NCERT Exemplar Class 9 Maths Chapter 12 solutions build a strong foundation of Heron’s Formula and stick to the syllabus recommended by CBSE. For the NCERT syllabus, books, notes, and class-wise solutions, refer to the NCERT.
| NCERT Exemplar Class 9 Maths Solutions Chapter 12: Exercise 12.1 Page: 113-114, Total Questions: 9 |
Question:1 An isosceles right triangle has area $8\; cm^{^{2}}$. The length of its hypotenuse is
(A) $\sqrt{32}\; cm$
(B) $\sqrt{16}\; cm$
(C) $\sqrt{48}\; cm$
(D) $\sqrt{24}\; cm$
Answer:
An isosceles right triangle is given.According to the definition of a right triangle, one angle should be 90o
According to the definition of isosceles trian angle any two sides equal.
i.e., are AB = BC
Suppose equal sides of the triangle be = x cm
[AB = BC = x]
Area of isosceles triangle = $\frac{1}{2}$ × base × height
$\Rightarrow$ 8 cm2 = $\frac{1}{2}$ × AB × BC
$\Rightarrow$ 8 × 2 = x × x [$\Theta$ AB = BC = x]
$\Rightarrow$ 16 =$x^{2}$
$\Rightarrow$ x = $\sqrt{16}$
$\Rightarrow$ x = 4 cm
So AB = BC = 4 cm
In $\Delta$ABC, using Pythagoras theorem
(AC)2 = (AB)2 + (BC)2
(AC)2 = (4)2 + (4)2
(AC)2 = 16 + 16
AC = $\sqrt{32}\; cm$
Hence hypotenuse of DABC is $\sqrt{32}\; cm$.
Hence option (A) is correct.
Question:2 The perimeter of an equilateral triangle is 60 m. The area is
(A) $10\sqrt{3}\; m^{2}$
(B) $15\sqrt{3}\; m^{2}$
(C) $20\sqrt{3}\; m^{2}$
(D) $100\sqrt{3}\; m^{2}$
Answer:
Given the perimeter of the equilateral triangle = 60 mSuppose the sides of an equilateral triangle, AB = BC = CA = x m
We know that the perimeter of an equilateral triangle = 3 × side
60 = 3 × x
60 = 3x
$\frac{60}{3}\; = x$
x = 20 m
i.e., sides AB = BC = CA = 20 m
We know that
Area of equilateral triangle = $\frac{\sqrt{3}}{4}\; \times \; side^{2}$
$\frac{\sqrt{3}}{4}\; \times \; \left ( 20 \right )^{2}\; = \frac{\sqrt{3}}{4}\; \times \;20\times \; 20$
= $\sqrt{3}$ × 5 × 20 = $\sqrt{3}$ × 100 = $100\sqrt{3}\; m^{^{2}}$
Hence area of equilateral triangle is $100\sqrt{3}\; m^{^{2}}$.
Hence option (D) is correct.
Question:3 The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is
(A) 1322 cm2
(B) 1311 cm2
(C) 1344 cm2
(D) 1392 cm2
Answer:
Given; In DABC, a = 56 cm, b = 60 cm, c = 52 cm
(Semi perimeter) S = $\frac{a+b+c}{2}$
S = $\frac{56+60+52}{2}$
S = $\frac{168}{2}\; = \; 84\; cm$
Using Heron’s formula
Area of triangle $= \sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$= \sqrt{84\left ( 84-56 \right )\left ( 84-60 \right )\left ( 84-52 \right )}$
$= \sqrt{84\times 28\times 24\times 32}$
$= \sqrt{7\times 3\times 2\times 2\times 2\times 2\times 7\times 2\times 2\times 6\times 2\times 4\times 4}$
$= \sqrt{7\times 7\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 3\times 3\times 4\times 4\times 2}$
= 7 × 2 × 2 × 2 × 2 × 4 × 3 = 1344 $cm^{^{2}}$
Hence area of DABC is 1344 $cm^{^{2}}$.
Hence option (C) is correct.
Question:4 The area of an equilateral triangle with side 2$\sqrt{3}$ cm is
(A) 5.196 cm2
(B) 0.866 cm2
(C) 3.496 cm2
(D) 1.732 cm2
Answer:
Given side of equilateral triangle $= \; 2\sqrt{3\;}\; cm$We know that area of equilateral triangle $= \; \frac{\sqrt{3}}{4}\; \times \left ( side \right )^{2}$
$= \; \frac{\sqrt{3}}{4}\; \times \left ( 2\sqrt{3} \right )^{2}$
$= \; \frac{\sqrt{3}}{4}\; \times\; 4\; \times \left ( \sqrt{3} \right )^{2}$ $\left [ \left ( \sqrt{3} \right )^{2}\; = \; \sqrt{3}\times \sqrt{3}\; = 3 \right ]$
$\frac{\sqrt{3}}{4}\; \times 4\times 3$
$\sqrt{3}\times 3$ = 1.732 × 3 [$\therefore \; \sqrt{3 }$ = 1.732]
= 5.196 $cm^{2}$
Hence the area of equity lateral triangle is 5.196 $cm^{2}$.
Hence option (A) is correct.
Question:5 The length of each side of an equilateral triangle having an area of $9\sqrt{3}\; cm^{2}$ is
(A) 8 cm
(B) 36 cm
(C) 4 cm
(D) 6 cm
Answer:
Given area of equilateral triangle $9\sqrt{3}cm^{2}$Let the side of the equilateral triangle be = a cm
$So\; we\; know\; that\; area\; of\; triangle\; = \frac{\sqrt{3}}{4}\times \left ( side \right )^{2}$
$9\sqrt{3}= \frac{\sqrt{3}}{4}\times \left ( side \right )^{2}$
$9\sqrt{3}= \frac{\sqrt{3}}{4}\times \left ( a \right )^{2}$ [$\therefore$ side = a]
$9\sqrt{3}\times 4\; = \; \sqrt{3}\times a^{2}$
$a^{2}= \; \frac{36\sqrt{3}}{\sqrt{3}}$
a2 = 36
a = $\sqrt{36}$
a = 6 cm
Hence, the side of an equilateral triangle is 6 cm.
Hence, option (D) is correct.
Answer:
Given area of equilateral triangle = $16\sqrt{3}cm^{2}$Suppose the side of the equilateral triangle is = a cm
We know that,
Area of equilateral triangle $= \frac{\sqrt{3}}{4}\left ( side \right )^{2}$
$16\sqrt{3}\; = \frac{\sqrt{3}}{4}\times \left ( a \right )^{2}$
$16\times 4\times \sqrt{3}= \sqrt{3}\times \left ( a \right )^{2}$
$\frac{64\times \sqrt{3}}{\sqrt{3}}= a^{2}$
a2 = 64
a = $\sqrt{64}$
a = 8 cm
Perimeter = 3a = 3(8) = 24 cm
Hence option (B) is correct.
Question:7 The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
(A) $16\sqrt{5}cm$
(B) $10\sqrt{5}cm$
(C) $24\sqrt{5}cm$
(D) 28 $cm$
Answer:
$Given\; a= \; 35cm,\; b= 54cm\; ,c= 61cm$
$S= \frac{a+b+c}{2}$
$S= \frac{35+54+61}{2}$
$\Rightarrow S= 75cm$
Using Heron's formula area of triangle $= \; \sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$= \; \sqrt{75\left ( 75-35 \right )\left ( 75-54 \right )\left ( 75-61 \right )}$
$= \sqrt{75\times 40\times 21\times 14}$
$= \sqrt{5\times 5\times 3\times 5\times 4\times 2\times 7\times 3\times 7\times 2}= \sqrt{5\times 5\times 5\times 3\times 3\times 2\times 2\times 2\times 2\times 7\times 7}$
$=$$5\times 3\times 2\times 7\times 2\sqrt{5}$
$= 420\sqrt{5}cm^{2}$
We know that area of $\bigtriangleup$ABC $= \frac{1}{2}\times base\times altitude$
$420\sqrt{5}= \frac{1}{2}\times 35\times AD$
$420\sqrt{5}\times 2= 35\times altitude$
$\Rightarrow \frac{420\sqrt{5}\times 2}{35}= \; altitude$
$\Rightarrow \frac{60\sqrt{5}\times 2}{5}= \; altitude$
$\Rightarrow 24\sqrt{5}= \; altitude$
$Hence,altitude\; is \; 24\sqrt{5}cm$
Hence option (C) is correct.
Question:8 The area of an isosceles triangle having a base 2of cm and the length of one of the equal sides 4 cm, is
(A) $\sqrt{15}cm^{2}$
(B) $\sqrt{\frac{15}{2}}cm^{2}$
(C) $2\sqrt{15}cm^{2}$
(D) $4\sqrt{15}cm^{2}$
Answer:
$We\; know\; that,$$We\; know\; that,semi-perimeter$
$S= \frac{a+b+c}{2}$
$S= \frac{2+4+4}{2}$
$S= \frac{10}{2}= 2cm$
Using Heron’s formula area of $\Delta$ABC $= \sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$= \sqrt{5\left ( 5-2 \right )\left ( 5-4 \right )\left ( 5-4 \right )}$
$= \sqrt{5\times 3\times 1\times 1}$
$= \sqrt{15}cm^{2}$
Hence, the area of the given triangle is $\sqrt{15}cm^{2}$.
Hence option (A) is correct.
Question:9 The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per $cm^{2}$ is
(A) Rs 2.00
(B) Rs 2.16
(C) Rs 2.48
(D) Rs 3.00
Answer:
To find the cost of painting, we have to find the area of the triangular board
Let the sides be denoted as, a = 6 cm, b = 8 cm, c = 10 cm
$semi-perimeter,S= \frac{a+b+c}{2}$
$S= \frac{6+8+10}{2}= \frac{24}{2}= 12cm$
We know that,
Using Heron’s formula, area of triangle $= \sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$= \sqrt{12\left ( 12-6 \right )\left ( 12-8 \right )\left ( 12-10\right )}$
$= \sqrt{12\times 6\times 4\times 2}$
$= \sqrt{6\times 2\times 6\times 2\times 2\times 2}$
$6\times 2\times 2= 24cm^{2}$
$Now\; cost\; of\; painting\; 1cm^{2}= 9\; paise= \frac{9}{100}Rs= 0.09Rs.$
$\left [ 1Rs= 100paise,1\; paise= \frac{1}{100}Rs \right ]$
$\therefore\; cost\; of\; painting\; 24cm^{2}= 24\times 0.09= 24\times \frac{9}{100}= Rs2.16$
Hence the cost of painting is Rs. 2.16.
Hence option (B) is correct.
| NCERT Exemplar Class 9 Maths Solutions Chapter 12: Exercise 12.2 Page: 115, Total Questions: 9 |
Answer:
Given a base of 4 cm and height of 6 cmWe know that,
$Area\; of\; triangle\; = \frac{1}{2}\times base\times height$
$= \frac{1}{2}\times 6\times 4= 3\times 4= 12cm\; ^{2}$
Therefore the given statement is false.
Answer:
Given, AB = AC = 4 cm and $\angle$A = $90^{\circ}$
.We know that
$Area\; of\; triangle= \frac{1}{2}\times base\times height$
$= \frac{1}{2}\times 4\times\; 4= 4\times 2= 8cm^{2}$
Hence, area of $\Delta$ is 8 $cm^{2}$ is True.
Answer:
Given$Area\; of\; isosceles\; triangle= \frac{5}{4}\sqrt{11}cm^{2}$
$Perimeter\; of\; triangle= 11cm$
We know that
$Perimeter= x+x+5 \; \; \; \; \; \; \; \; \; \; \left [ \therefore Let\; equal\; sides\; of\; triangle= x \right ]$
$11cm-5cm= 2x$
$\Rightarrow 6cm= 2x\Rightarrow x= \frac{6}{2}cm$
$\Rightarrow x=3cm$
Now, in the right triangle ADB
Using Pythagoras theorem
$\left ( AB \right )^{2}=\left ( AD \right )^{2}+\left ( BD \right )^{2}$
$\left ( 3 \right )^{2}=\left ( AD \right )^{2}+\left ( \frac{5}{2} \right )^{2}$
$9-\frac{25}{4}=\left ( AD \right )^{2}$
$\Rightarrow AD= \sqrt{9-\frac{25}{4}}$
$\Rightarrow AD= \sqrt{\frac{36-25}{4}}$
$AD= \sqrt{\frac{11}{4}}=\frac{\sqrt{11}}{2}CM\; \; \; \; \; \; \; \left [ Q\sqrt{4} =\sqrt{2\times 2}=2\right ]$
$Area\; of\; isosceles\; triangle=\frac{1}{2}\times base\times height$
$= \frac{1}{2}\times 5\times\frac{\sqrt{11}}{2}=\frac{5\sqrt{11}}{4}cm^{2}$
Therefore the given statement is true.
Answer:
[False]$Area\; of\; equilateral\; triangle =\frac{\sqrt{3}}{4}side^{2}$
$Required \; area =\frac{\sqrt{3}}{4}\times \left ( 8 \right )^{2}$
$=\frac{\sqrt{3}}{4}\times 8\times 8\; =16\sqrt{3}cm^{2}$
Therefore the given statement is false.
Answer:
$Side\; of\; rhombus = 10 cm$$One\; Diagonal = 16 cm$
We know that the diagonals of a rhombus intersect each other at a right angle
$So\; In\; right\; \Delta AOB$
$Using\; Pythagoras\; theorem$
$(AB)^{2} = (OA)^{2} + (OB)^{2}$
$(10)^{2} = (8)^{2} + (OB)^{2}$
$100 = 64 + (OB)^{2}$
$100 -64=\left ( OB \right )^{2}$
$(OB)^{2} = 36$
$OB=\sqrt{36} \; \; \; \; \; \; \; \left [ Q\sqrt{36}=\sqrt{6\times 6}=6 \right ]$
$OB = 6 cm$
$\therefore BD = 2\; \times \; OB$
$BD = 2 \times 6 = 12 cm$
$Now, Area\; of\; rhombus = \frac{1}{2}\; \times product\; of \; its\; diagonals$
$= \frac{1}{2} \times BD \times AC$
$=\frac{1}{2} \times 12 \times 16$
$= 6 \times 16 = 96 cm^{2}$
Hence, the area of a rhombus is 96 $cm^{2}$
Therefore the given statement is true.
Answer:
We know that$Area\; of\; parallelogram = base \times height$
$= 10 \times 3.5$
$= 10 \times \frac{35}{10} =35cm^{2}$
Hence, the area of a parallelogram is $35cm^{2}$
Therefore the given statement is false.
Answer:
According to question$Area\; of\; regular\; hexagon = sum\; of\; area \; of\; five\; equilateral \; triangles$
We know that a regular hexagon is divided into 6 equilateral triangles by its diagonals.
$Area\; of\; 1\; equilateral\; triangle = \frac{\sqrt{3}}{4} \times a^{2}$
$Area\; of\; 6\; equilateral\; triangle =6\times \frac{\sqrt{3}}{4} \times a^{2}=\frac{3\sqrt{3}}{2}a^{2}$
$Area\; of\; 5\; equilateral\; triangle =5\times \frac{\sqrt{3}}{4} \times a^{2}=\frac{5\sqrt{3}}{2}a^{2}$
Therefore the given statement is false.
Answer:
$Let\; a = 51 \; m, b = 37\; m \; and \; c = 20\; m$
$S=\frac{51+37+20}{2}=\frac{108}{2}=54m$
We know that using Heron’s formula
$Area\; of \; triangle AB=\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{54\left ( 54-51 \right )\left ( 54-37 \right )\left ( 54-20 \right )}$
$=\sqrt{54\times 3\times 17\times 34}$
$=\sqrt{9\times 3\times 2\times 3\times 17\times 17\times 2}$
$=\sqrt{3\times3\times 3\times 3\times 2\times 2\times 17\times 17}$
=$3\times 3\times 2\times 17$
$= 306m^{2}$
To find cost :
Cost of levelling 1 m2 = Rs 3
$\therefore Cost\; of\; levelling\; 306\; m^{2} = \; 3 \times 306 = Rs.\; 918$
Therefore the given statement is true.
Answer:
$Let \; a\; =\; 11\; cm ;\; b\; =\; 12\; cm\; ;\; c = 13 cm$$Semi perimeter (S) = \frac{a+b+c}{2}$
$= \frac{11+12+13}{2}$
$= \frac{36}{2}=18cm$
$(Area\; of\; triangle \; ABC)\; by\; Heron's\; formula$
$=\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{18\left ( 18-11 \right )\left ( 18-12 \right )\left ( 18-13\right )}$
$= \sqrt{18\times 7\times 6\times 5}$
$= \sqrt{6\times 3\times 7\times 6\times 5}$
$= \sqrt{6^{2}\times 3\times 7\times 5}$
$= 6\sqrt{3\times 7\times 5}$
$= 6\sqrt{105}$ $\because \sqrt{105}=10.2469\simeq 10.25$
$= 6 \times 10.25$
$= 61.5 cm^{2}$
$Given\; altitude\; =\; 10.25\; cm\; and$
$Its \; corresponding\; base \; = \; 12\; cm$
$Area\; of \times triangle ABC = \frac{1}{2} \times Base \times corresponding\; Height$
$= \frac{1}{2} \times 12 \times 10.25$
$=61.5cm^{2}$
Hence the area obtained is the same.
Therefore the given statement is true.
| NCERT Exemplar Class 9 Maths Solutions Chapter 12: Exercise 12.3 Page: 117, Total Questions: 10 |
Answer:
$Rs.10500$To find the cost, firs,t we have to find the area of this triangular field.
$Let \; sides\; be\; a = 50\; cm ; b = 65\; cm ; c = 65 \; m$
$Semi\; perimeter(s) = \frac{a+b+c}{2}$
$= \frac{50+65+65}{2}$
$= \frac{180}{2}$
= 90
Area of Triangular field:
$By\; herons\; formula =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{90\left ( 90-50\right )\left ( 90-65 \right )\left ( 90-65 \right )}$
$=\sqrt{90\times 40\times 25\times 25}$
$=\sqrt{9\times 10\times 4\times 10\times \left ( 5^{} \right )^{2}\times \left ( 5 \right )^{2}}$
=$3\times 10\times 2\times 5^{2}$
= $30\times 2\times 25$
$= 1500m^{2}$
$Rate\; of\; laying \; grass = 7\; Rs \; per\; m^{2}$
$Cost\; of \; laying \; grass\; for\; 1500 m^{2} = Rs (7 \times 1500)$
$= 10500\; Rs$
$Hence\; the \; answer\; is\; 10500 Rs.$
Answer:
$Here \; sides\; of \; triangular\; walls\; are \; a = 14 m, b = 15 m \; and \; c = 13 m$
We have to find the area of this triangle
Using Heron’s formula, semi-perimeter:
$S=\frac{a+b+c}{2}=\frac{14+15+13}{2}=\frac{42}{2}=21m$
$The\; area\; of\; triangular\; wall =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{21\left ( 21-13\right )\left ( 21-14 \right )\left ( 21-15 \right )}$
$={\sqrt{21\times 8\times 7\times 6}}$
$= \sqrt{3\times 7\times 2\times 2\times 2\times 7\times 2\times 3}$
$= \sqrt{\left ( 2\times 2\times 2\times 2 \right )\times \left ( 3\times 3\times 7\times 7 \right )}$
$= 2\times 2\times 3\times 7=84m^{2}$
Given that the advertisements yield earnings per m2 for 1 year=RS 2000
$Earnings\; per\; m^{2} \; per\; month =Rs.\left ( \frac{2000}{12} \right )$
$Earnings\; per\; m^{2}\; for\; 6\; months =Rs.\; \left ( \frac{2000}{12}\times 6 \right )$
$Earnings\; for\; 84 m^{2}\; for\; 6 \; months =Rs\left ( \frac{2000}{2}\times 84 \right ) Rent \; the\; company\; has\; to\; pay$
$Rent \; the\; company \; has\; to\; pay = Rs. 2000 \times 42 = Rs. \; 84000$
$Hence\; company\; has\; to\; pay\; Rs.\; 84000.$
Answer:
Here $\Delta$ABC is an equilateral triangle i.e.AB = BC = CA = x (Let)
Now we can see here three perpendicular
$OX \perp AB, OZ \perp BC, OY \perp AC$
$OX = 10 cm, OY = 14 cm\; and\; OZ = 6 cm$
$So\; that\; area\; of\; \Delta ABC = Ar(\Delta AOC) + Ar(\Delta BOC) + Ar(\Delta AOB)$
$\frac{\sqrt{3}}{4} side^{2}=\frac{1}{2} \times base \times height + \frac{1}{2} \times base \times height + \frac{1}{2} \times base \times height$
$[\Theta \Delta ABC\; is\; equilateral\; \Delta ,so\; area\; of\; equilateral\; \Delta = \frac{\sqrt{3}}{4}side^{2} ]$
$\Rightarrow \frac{^{\sqrt{3}}}{4}\times x^{2}=\frac{1}{2}\times AC\times OY+\frac{1}{2}\times BC\times OZ+\frac{1}{2}\times AB\times OX$
$Taking\; \frac{1}{2} \; common$
$\frac{\sqrt{3}}{4}\times x^{2}=\frac{1}{2}\times \left [ AC\times OY+BC\times OZ+AB\times OX \right ]$
$\frac{\sqrt{3}}{4}\times x^{2}=\frac{1}{2}\times \left [ AC\times OY+AC\times OZ+AC\times OX \right ]$
[$\Theta$ AB = BC = AC, $\Delta$ABC equilateral triangle]
$\frac{\sqrt{3}}{4}\times x^{2}=\frac{1}{2}AC\times \left [ OY+OZ+OX \right ]$
$\frac{\sqrt{3}}{4}\times x^{2}=\frac{1}{2}AC\times \left [ 14+6+10 \right ]$
$\frac{\sqrt{3}}{4}\times x^{2}=\frac{1}{2}AC\times \left [ 30 \right ]$
$\frac{\sqrt{3}}{4}\times x^{2}=15\times AC$
$\sqrt{3}\times x^{2}=15\times x\times 4\; \; \; \; \; \; [\because AC = BC = AC = x]$
$\frac{x^{2}}{x}=\frac{15\times 4}{\sqrt{3}}$
$x=\frac{60}{\sqrt{3}}cm$
$Hence \; the\; length\; of\; the\; sides\; of\; \Delta ABC\; is\; \frac{60}{\sqrt{3}}cm$
$Area\; of\; \Delta ABC =\frac{\sqrt{3}}{4}\times \left ( \frac{60}{\sqrt{3}} \right )^{2}=\frac{\sqrt{3}}{4}\times \frac{60}{\sqrt{3}}\times \frac{60}{\sqrt{3}}$
$=\frac{15\times 60}{\sqrt{3}}=\frac{900}{\sqrt{3}}$
On rationalisation
$\frac{900}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{900\times \sqrt{3}}{3}=300\sqrt{3}cm^{2}$
Answer:
$Given\; perimeter\; of\; isosceles\; triangle = 32 cm$$We\; have\; ratio\; of\; equal\; side\; and\; base = 3 : 2$
$Thus,\; let\; the \; sides\; of\; triangle\; be\; AB = AC = 3x\; and\; BC = 2x$
$\therefore Perimeter \; of\; a\; triangle = 32 cm$
$3x + 3x + 2x = 32$
$8x = 32$
$x=\frac{32}{8}$
$x = 4 cm$
$So, AC = AB = 3 \times 4 cm\; and\; BC = 2 \times 4 cm$
$AC = AB = 12 cm\; and \; BC = 8 cm$
$Now, a = 8\; cm, b = 12\; cm, c = 12 \; cm$
Using Heron’s formula
$S= \frac{a+b+c}{2}=\frac{8+12+12}{2}=\frac{32}{2}=16cm$
$\therefore\; Area \; of\; isosceles\; triangle\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{16\left ( 16-8 \right )\left ( 16-12 \right )\left ( 16-12 \right )}$
$= \sqrt{16\times 8\times 4\times 4}$
$= \sqrt{4\times 4\times 4\times 2\times 4\times 4}$
$=4\times 4 \sqrt{ 2\times 2\times 2}=4\times 4\times 2\sqrt{2}=32\sqrt{2}\; cm^{2}$
$Hence,\; the\; area\; of\; isosceles \; triangle\; is\; 32\sqrt{2}\; cm^{2}$
Answer:
$Length\; of\; the\; altitude \; from\; vertex\; A\; on\; the\; side\; DC = 15\; cm$
We know $A B=C D$ and $A D=B C \quad[\because A B C D$ is a parallelogram $]$
$Area \; of\; parallelogram = 2 \times area \; of\; \Delta DBC$
$So \; here\; \Delta DBC\; sides\ having\; DB = 25 cm, BC = 17cm\;and\;CD = 12 cm$
Using Heron’s formula
$S=\frac{25+17+12}{2}=\frac{54}{2}=27cm$
$Area \; of\; \; triangle\; \Delta DBC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{27\left ( 27-25 \right )\left ( 27-17 \right )\left ( 27-12 \right )}$
$= \sqrt{27\times 2\times 10\times 15}$
$= \sqrt{9\times 3\times 2\times 5\times 2\times 5\times 3}$
$= \sqrt{3\times 3\times 3\times 3\times 5\times 5\times 2\times 2}$
$= 2\times 3\times 3\times 5=90\; cm^{2}$
$\\ Area\; of\; parallelogram \; ABCD = 2 \times Ar(\Delta DBC) = 2 \times 90 cm^{2} = 180 cm^{2}.$
$We \; know \; that\; area\; of\; parallelogram = base \times height$
$= base\; CD \times length\; of\; the \; altitude\; from \; vertex\; A \; on\; the\; side\; DC$
$180\; cm^{2} = 12\; cm \; (length\; of\; the \; altitude\; from\; vertex\; A\; on\; the\; side\; DC)$
$\\Length\; of\; the \; altitude\; from \; vertex\; A\; on\; the\; side\; DC=180/12 = 15 cm.$
Hence, the length of the altitude from vertex A on the side DC = 15 cm
Answer:
We know that ABCD is a parallelogramSo the opposite sides are equal.
AB = CD = 60 m, AD = BC = 40 m
$Thus, Area\; of\; parallelogram = 2 \times Ar(\Delta ABC)$
In $\Delta$ABC, using heron’s formula
$Semi perimeter, S =\frac{60+40+80}{2}=\frac{180}{2}=90m$
$Area \; of\; \; triangle\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{90\left ( 90-60 \right )\left ( 90-40 \right )\left ( 90-80 \right )}$
$=\sqrt{90\times 30\times 50\times 10}$
$=\sqrt{3\times 30\times 30\times 10\times 10\times 5}$
$= 30\times 10\sqrt{3\times 5}=300\sqrt{15}\; m^{2}$
$Hence,\; area\; of\; parallelogram =2\times 300\sqrt{15}\; m^{2}=600\sqrt{15}\; m^{2}$
Answer:
Given perimeter of a triangular field = 420 m and ratio of sides = 6 : 7 : 8Let the sides of triangular field be = 6x, 7x and 8x
$\therefore Perimeter\; of\; triangular\; field = 6x + 7x +\; 8x$
$420 = 6x + 7x + 8x$
$420 = 21x$
$x=\frac{420}{21}$
$x = 20$
$Then\; sides\; are\; 6 \times 20 = 120m, 7 \times 20 = 140m\; and \; 8 \times 20 = 160m$
Using Heron’s formula for finding the area of $\Delta$ABC
a = 120m, b = 140m, c = 160m
$S=\frac{a+b+c}{2}=\frac{120+140+160}{2}=\frac{420}{2}=210m$
$Area \; of\; \; triangle\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{210\left ( 210-120 \right )\left ( 210-140 \right )\left ( 210-160\right )}$
$= \sqrt{210\times 90\times 70\times 50}$
$= \sqrt{7\times 30\times 3\times 30\times 7\times 10\times 5\times 10}$
$= \sqrt{7\times 7\times 10\times 10\times 30\times 30\times 3\times 5}$
= $2100\sqrt{15}\; m^{2}$
Answer:
Here we have, AB = 6 cm, BC = 8 cm, CD = 12 cm and AD = 14 cmAccording to the question, the angle between AB and BC is $90^{\circ}$
Join AC
In Right $\Delta$ABC, [By Pythagoras theorem]
$AC^{2} = (6)^{2} + (8)^{2}$
$AC^{2} = 36 + 64$
$AC = \sqrt{100}$
$AC = 10 cm$
$Area\; of \; quadrilateral \: ABCD = Ar(\Delta ABC) + Ar(\Delta ACD)$
$Now, we\: find \; area\; of \; \Delta ABC = \frac{1}{2} \times base \times height$
$= \frac{1}{2}\times BC\times AB= \frac{1}{2}\times 8\times 6= (4 \times 6) cm^{2}$
$Area of \Delta ABC = 24 cm^{2}$
$In \Delta ACD, AC = a = 10 cm, CD = b = 12 cm, AD = c = 14 cm$
$S= \frac{a+b+c}{2}= \frac{10+12+14}{2}= \frac{36}{2}= 18cm$
$Using\; Heron's \; formula \; area \; of \Delta ACD=\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$= \sqrt{18\left ( 18-10 \right )\left ( 18-12 \right )\left ( 18-14 \right )}$
$= \sqrt{18\times 8\times 6\times 4}$
$= \sqrt{9\times 2\times 4\times 2\times 3\times 2\times 4}$
$= \sqrt{3\times 3\times 2\times 2\times 3\times 2\times 4\times 4}$
$= 3\times 2\times 4\times \sqrt{3\times 2}= 24\sqrt{6}\; cm^{2}$
$Hence, area \; of\; quadrilateral \; ABCD = 24cm^{2}+24\sqrt{6}\; cm^{2}$
Answer:
Let ABCD be a rhombus thus AB = BC = CD = DA = x (Let)
$We \; have\; perimeter \; of \; rhombus = 40 cm$
$\Rightarrow AB + BC + CD + DA = 40 cm$
$\Rightarrow x + x + x + x = 40 cm$
$\Rightarrow 4x = 40 cm$
$\Rightarrow x = \frac{40}{4} cm$
$\Rightarrow x = 10 cm$
$\therefore sides \; of \; rhombus \; AB = BC = CD = DA = 10 cm$
Area of rhombus = 2 $\times$ Ar($\Delta$ABC) [diagonal of rhombus divides it into two triangles of equal area]
Now, we find the area of the triangle using Heron’s formula
$In\; \Delta ABC, S=\frac{a+b+c}{2}= \frac{10+10+12}{2}= \frac{32}{2}= 16cm$
$Area \; of\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{16\left ( 16-10 \right )\left ( 16-10 \right )\left ( 16-12 \right )}$
$= \sqrt{16\times 6\times 6\times 4}$
$= \sqrt{8\times 8\times 6\times 6\times 4}$
$= \sqrt{4\times 4\times 6\times 6\times 4}$
$= 4\times 6\sqrt{2\times 2}$
$= 4\times 6\times 2= 48cm^{2}$
Now, Area of rhombus = 2 $\times$ Ar($\Delta$ABC)
$= 2\times 40cm^{2}= 96cm^{2}$
We find the cost of painting
Thus,
$\because cost\; of \; painting\; the\; sheet \; of\; 1 cm^{2} = Rs.\; 5$
$\therefore cost \; of\; painting\; the \; sheet\; of \; 96\; cm^{2}= Rs.\; 96 \times 5 = Rs.\; 480$
Hence, the cost of the painting on both sides of the sheet = 2 $\times$ 480 = Rs. 960.
Question:10 Find the area of the trapezium PQRS with height PQ given in Figure.
Answer:
$Firstly\; we\; have\; side \; PS = 12 m, SR = 13, QR = 7 m$
Join RT
So here PT = PS – ST
PT = 12 m – 5 m
PT = 7 m
and ST = PS – PT
$ST = \left ( 12-7 \right )m$
ST = 5 m
Now, In $\Delta$STR, Using Pythagoras theorem
$We\; get, (SR)^{2} = (ST)^{2} + (TR)^{2}$
$(13)^{2} = (5)^{2} + (TR)^{2}$
$169 = 25 + (TR)^{2}\; \; \; \; \; \; \; \; \; \; \; [(13)^{2} = 169 \; and\; (5)^{2} = 25]$
$169 - 25 = (TR)^{2}$
$144 = (TR)^{2}\; \; \; \; \; \; \; \; \; \; \; \; [ \sqrt{144} = 12]$
$TR = 12cm\; \; \; \; \; \; \; \; \; \; \; \; [ \sqrt{12\times 12} = 12]$
Now, we can find the area of the trapezium
$Area \; of\; trapezium = \frac{1}{2} \times [sum\; of \; parallel\; sides] \times height$
$= \frac{1}{2}\times \left [ 12+7 \right ]\times 12$
$= 19\times 6\; cm^{2}$
$= 114\; cm^{2}$
$Hence, the\; area\; of\; trapezium\; is\; 114\; cm^{2}.$
| NCERT Exemplar Class 9 Maths Solutions Chapter 12: Exercise 12.4 Page: 118-120, Total Questions: 8 |
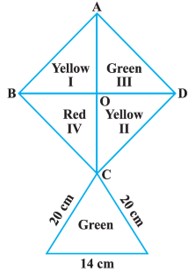
Answer:
$Red = 242 \; cm^{2}$$Yellow = 484\; cm^{2}$
$Green = 373.14 \; cm^{2}$
$Given,\; ABCD\; is\; a\; square.$
We know that all sides of a square are equal
AB = BC = CD = DA and
$\angle A = \angle B = \angle C = \angle D = 90^{\circ} [\because \; All\; angles\; of\; a\; square\; are\; 90^{\circ}]$
$In \Delta ABC,\; using \; Pythagoras \; theorem$
$(AC)^{2} = (AB)^{2}+ (BC)^{2}$
$(44)^{2} = (AB)^{2}+ (BC)^{2}\; \; \; \; \; \; \; \; [\Theta \; AB = BC\; equal\; sides]$
$44\times 44=2\left ( AB \right )^{2}$
$\frac{44\times 44}{2}=\left ( AB \right )^{2}$
$(AB)^{2} = 22 \times 44$
Taking square root on both sides
$\sqrt{\left ( AB \right )^{2}}=\sqrt{22\times 44}$
$AB=\sqrt{22\times 2\times 22}$
$AB=22\sqrt{2}$
$AB = BC = CD = DA =22\sqrt{2}\; cm$
$Now,\; Area\; of \; square\; ABCD = (side)^{2}$
$=\left ( 22\sqrt{2}\right )^{2}=22\times 22\times \sqrt{2}\times \sqrt{2}$
$= 484\times \sqrt{2\times 2}=484\times 2$
$Area\; of\; square\; ABCD = 968\; cm^{2}$
But square ABCD is divided into four coloured squares.
$So,\; area\; of\; Yellow \; I =\frac{968}{4}= 242 cm^{2}$
$Area\; of\; Yellow \; II =\frac{968}{4}= 242 \; cm^{2}$
$Area\; of\; Green \; III =\frac{968}{4}= 242 \; cm^{2}$
$Area\; of\; Red \; IV =\frac{968}{4}= 242 \; cm^{2}$
$Total\; yellow\; area\; = 242\; cm^{2} + 242\; cm^{2} = 484\; cm^{2}$
We have to find the lower triangle of green colour as well.
$Let\; a = 20\; cm, b = 20\; cm, c = 14\; cm$
$Semi\; perimeter(s) = \frac{a+b+c}{2}$
$= \frac{20+20+14}{2}$
$= \frac{54}{2}=27$
Area of Triangular field:
$By\; heron's\; formula =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{27\left ( 27-20\right )\left ( 27-20 \right )\left ( 27-14 \right )}$
$= \sqrt{3\times 3\times 3\times 7\times 7\times 13}$
$= 21\sqrt{3\times 13}$
$= 131.14\; cm^{2}$
$So\; total\; green\; area\; = 242 + 131.14 = 373.14\; cm^{2}$
$Hence,\; paper\; required$
$Red = 242\; cm^{2}$
$Yellow = 484\; cm^{2}$
$green = 373.14\; cm^{2}$
Answer:
$\left [ 20\sqrt{30}\; cm^{2} \right ]$Let the smaller side of the triangle be x cm
Let BC = x cm
According to the question,
One side of a triangle is 4 cm longer than the smaller side
Let this side be AC = x + 4
Also, the third side is 6 cm less than twice the smaller side
Let this side be AB = (2x - 6) cm
Given perimeter of $\Delta$ABC = 50 cm
x + x + 4 + 2x - 6 = 50
$4x - 2 = 50$
$4x = 50+2$
$4x = 52$
$x = \frac{52}{4}$
$x = 13 \; cm$
$So\; the\; side \; AC = (x + 4) = (13 + 4) = 17\; cm$
$Side\; AB = \left ( 2x-6 \right )\; cm= \left ( 26-6 \right )\; cm= 20\; cm$
Now in $\Delta$ABC, a = 13 cm, b = 17 cm, and c = 20 cm
Using Heron’s formula
$S= \frac{a+b+c}{2}= \frac{13+17+20}{2}= \frac{50}{2}= 25\; cm$
$Area \; of\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{25\left ( 25-13 \right )\left ( 25-17 \right )\left ( 25-20 \right )}$
$=\sqrt{25\times 12\times 8\times 5}$
$=\sqrt{5\times 5\times 2\times 2\times 3\times 2\times 2\times 2\times 5}$
$=\sqrt{5\times 5\times 5\times 2\times 2\times 2\times 2\times 2\times 3}$
$= 5\times 2\times 2\sqrt{30}$
$Area \; of \; \Delta ABC = 20\sqrt{30}\; cm^{2}$
$Hence\; the \; area\; of\; triangle\; is \; 20\sqrt{30}\; cm^{2}$
Answer:
Let the smaller parallel side be CD = x cm
The other parallel side AB = (x + 4) cm
Given, area of trapezium = 475 $cm^{2}$
Height DE = 19 cm
$We \; know \; that, \; Area \; of \: trapezium = \frac{1}{2} \times height \times (sum\; of \; parallel \; sides)$
$475= \frac{1}{2}\times DE\times \left ( DC+AB \right )$
$475\times 2= 19\times \left ( x+x+4 \right )$
$\frac{475\times 2}{19}= 2x+4$
25 $\times$ 2 = 2x + 4
50 = 2x + 4
50 - 4 = 2x
46 = 2x
$x= \frac{46}{2}$
x = 23 cm
So the smaller side CD is 23 cm and the other parallel side AB is (23 + 4) cm = 27 cm.
Answer:
Let ABCD be the rectangular plot,AB = 40 cm, AD = 15 cm
Given that a minimum of 3 m wide space should be left in the front and back
$length \; of \; PQ = [AB - (3 + 3)] \; m$
$PQ = [40 - 6] \; m$
$PQ = 34 \; m$
Similarly, RS = 34 m
Given that 2 m wide space on each of other sides is to be left
$Length\; of \; PS = [AD - (2 + 2)] \; m$
$PS = [15 - 4] \; m$
$PS = 11 \; m \; and$
$QR = 11 \; m$
So here PQRS is another rectangle formed in the rectangle ABCD
So, Area of rectangle PQRS = length $\times$ breadth
$= PQ\times PS= \left ( 34\times 11 \right )\; m^{2}= 374\; m^{2}$
Hence the area of the house can be constructed in 374 $m^{2}$
Answer:
Given, ABCD is trapezium having parallel side AB = 90 m, CD = 30 m
Draw DE parallel to CB
So, BE = 30 m
Now, AE = (AB - EB)
AE = (90 - 30) m
AE = 60 m
So, in right triangle $\Delta$AED
$\left ( AD \right )^{2}= (AE)^{2} + (DE)^{2} \: \; \; \; \; \; [Using Pythagoras theorem]$
$\left ( 100 \right )^{2}= (60)^{2} + (DE)^{2}$
$10000= 3600+(DE)^{2}$
$10000- 3600= (DE)^{2}$
$6400= (DE)^{2}$
Taking square root on both sides
$\sqrt{6400}= \sqrt{(DE)^{2}}$
DE = 80 m
$We\; know \; that\; the \; area \; of \; trapezium \; ABCD = \frac{1}{2} \times (sum \; of \; parallel \; sides) \times height$
$= \frac{1}{2} \times (AB+CD) \times DE$
$= \frac{1}{2} \times (90+30) \times 80$
$= 120\times 40= 4800\; m^{2}$
$\because \; cost \; of\; ploughing \; 1 m^{2} \; field = Rs \; 4$
$\therefore \; cost \; of \; ploughing \; 4800 \; m^{2}\; field = 4800 \times 4 = Rs. \; 19200$
Hence the total cost of ploughing the field is Rs. 19200.
Answer:
AB = 7.5 cm, AC = 6.5 cm, BC = 7 cm
Let a = 7.5 cm, b = 6.5 cm, c = 7 cm
$Now, S=\frac{a+b+c}{2}=\frac{7.5+6.5+7}{2}=\frac{21}{2}=10.5\; cm$
$Area\; of\; \Delta ABC,\; By\; heron's\; formula =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{10.5\left ( 10.5-7.5 \right )\left ( 10.5-6.5 \right )\left ( 10.5-7 \right )}$
$=\sqrt{10.5\times 3\times 4\times 3.5}$
$=\sqrt{\frac{105}{10}\times 3\times 4\times \frac{35}{10}}$
$=\sqrt{21\times 3\times 7}=\sqrt{3\times 7\times 3\times 7}=3\times 7=21\; cm^{2}$
$Now,\; we\; find\; the \; length\; DF \; of\; parallelogram\: DBCE$
$Area\; of\; parallelogram = base \times height = BC \times DF$
$Area\; of\; parallelogram = 7DF$
According to the question,
$Area\; of\; \Delta ABC = Area \; of\; parallelogram DBCE$
$21 = 7DF$
$\frac{21}{7}= DF$
$DF = 3\; cm$
$Hence\; height\; of\; parallelogram\; is\; 3\; cm.$
Answer:
$Given, BC = 51\; cm \; and \; CD = 25\; cm$$Area \; of\; rectangle\; ABCD = (51 \times 25) cm^{2}$
$In\; trapezium\; PQCD\; , parallel\; sides\; QC\; and\; PD\; are\; in\; the\; ratio\, 9:8$
Let length of QC = 9x and PD = 8x
$We\; have\: , Area\: of\: trapezium\: PQCD = \frac{5}{6}th\: part\; of\; Area(ABCD)$
$\frac{1}{2} \times (Sum\; of\; ||\; sides) \times height =\frac{5}{6} \times length \times breadth$
$\frac{1}{2}\times (PD + QC) \times CD = \frac{5}{6}\times BC \times CD$
$\frac{1}{2} \times (8x + 9x) \times 25 = \frac{5}{6}\times 51 \times 25$
$\frac{1}{2}\times 17x \times 25 = \frac{5}{6}\times 51 \times 25$
$\frac{25}{2}\times 17x = \frac{5}{6}\times 51 \times 25$
$x = \frac{5}{6}\times 51 \times 25\times \frac{1}{17}\times \frac{2}{25}$
$x = 5$
$PD = 8x$
$= 8\times 5$
$= 40\; cm$
$QC = 9x$
= 9 x 5 = 45
Answer:
We have the dimensions of the rectangle tile as 50 cm × 70 cmWe know that the area of a rectangle = length × breadth
Given sides of triangular design: 26 cm, 17 cm, 25 cm
To find the area using Heron’s formula
Let, a = 26 cm, b = 17 cm, c = 25 cm
$S=\frac{a+b+c}{2}=\frac{26+17+25}{2}=\frac{68}{2}=34\; cm$
$Area\; of\; triangle =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$
$=\sqrt{34\left ( 34-26 \right )\left ( 34-17 \right )\left ( 34-25 \right )}$
$= \sqrt{34\times 8\times 17\times 9}$
$= \sqrt{17\times 2\times 2\times 2\times 2\times 17\times 3\times 3}$
$= 2\times 2\times 3\times 17$
Area of $\Delta$ABC = 204 $cm^{2}$
But we have 8 triangles of equal area
So area of design = 8 × area of one $\Delta$
= 8 × 204 = 1632 $cm^{2}$The remaining area of tile = Area of tile - Area of design
= (3500 – 1632) $cm^{2}$ = 1868 $cm^{2}$
Hence the area of the design is 1632 $cm^{2}$ and the remaining area of the tile is 1868 $cm^{2}$.
Important Topics for NCERT Exemplar Solutions Class 9 Maths Chapter 12:
Key topics covered in NCERTExemplarr Class 9 Maths Solutions chapter 12 are:
- How to find out the area of a triangle using base length and height.
- How to find out the area of a triangle using Heron’s Formula.
- NCERT Exemplar Class 9 Maths Solutions Chapter 12 explains how Heron’s formula can be used to find out the area of a quadrilateral.
NCERT Exemplar Class 9 Maths Solutions Chapter
NCERT Class 9 Exemplar Solutions Subject-Wise:
Given below are the subject-wise exemplar solutions of class 9 NCERT:
NCERT Solutions for Class 9 Mathematics: Chapter-wise
NCERT Class 9 Exemplar Solutions for Other Subjects
NCERT Solution Subject Wise
Here are the subject-wise links for the NCERT solutions of class 9:
Check NCERT Notes Subject Wise
Given below are the subject-wise NCERT Notes of class 9:
Also, check NCERT Books and NCERT Syllabus here
Here are some useful links for NCERT books and the NCERT syllabus for class 9:
Frequently Asked Questions (FAQs)
Q: Is Heron’s formula applicable in finding the area of a scalene triangle?
A:
Yes, we can find out the area of any triangle if three sides of a triangle are known by using the heron’s formula.
Q: Is Heron Formula have any limitation to find out area of triangle?
A:
No, we can use heron’s formula to find out the area of any triangle if sides are given.
Q: If we know the perimeter of an equilateral triangle, can we find out the area of this triangle?
A:
In an equilateral triangle, all sides have equal length, therefore if we know the perimeter of triangle, we know each side length. Now by using hero formula we can find out area of this equilateral triangle.
Q: How we can find out area of triangle?
A:
We can find out area of triangle by two methods. If we know the base length and height of triangle then half of their product will give the area of triangle. If we know three sides of the triangle, we can use hero formula to find out area of triangle
Q: What is weightage of the chapter on Heron’s Formula in the final examination?
A:
This chapter concludes to around 5-7% marks of the final paper. Generally, the type of questions that can be expected from this chapter is MCQs and short answer-type questions. NCERT exemplar Class 9 Maths solutions chapter 12 is adequate to practice, understand and score well in the examinations.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters