NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
In the world of geometry, quadrilaterals teach us that shape and structure can come in many forms. Have you noticed that the things surrounding you, like windows, doors, your notebook or tablet, all have a similar four-sided shape? Well, these four-sided shapes are called quadrilaterals. The beauty of quadrilaterals lies in their diversity—trapeziums, parallelograms, rectangles, squares, and rhombuses all under one family. In the chapter Quadrilaterals, students will learn the concepts of Properties of a Parallelogram, theorems related to angles and sides, the Mid-point Theorem, etc. These NCERT Solutions for Class 9 will help the students grasp more advanced geometry concepts easily and enhance their problem-solving ability in real-world applications.
This Story also Contains
- Quadrilaterals Class 9 Questions And Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals: Exercise Questions
- Quadrilaterals Class 9 NCERT Solutions: Exercise-wise
- Class 11 Maths NCERT Chapter 8: Extra Question
- Quadrilaterals Class 9 Chapter 8: Topics
- Quadrilaterals Class 9 NCERT Solutions: Important Formulae And Points
- Approach to Solve Questions of Quadrilaterals Class 9
- NCERT Solutions For Class 9 Mathematics - Chapter Wise
Understanding the properties of sides, angles, and diagonals is key to mastering Quadrilaterals. These NCERT Solutions for class 9 Maths provide easy-to-follow step-by-step solutions for all the exercise problems. Students who are searching for Quadrilaterals class 9 solutions will find this article beneficial. The article covers all the important Class 9 Maths Chapter 8 question answers. These NCERT Solutions are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
Quadrilaterals Class 9 Questions And Answers PDF Free Download
To make maths learning easier, Careers360 experts have created these NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals: Exercise Questions
Below are the detailed NCERT Class 9 Maths Chapter 8 Quadrilaterals question answers provided in the textbook.
| Quadrilaterals Class 9 Question Answers: Exercise: 8.1 Page number: 110-111 Total Questions: 7 |
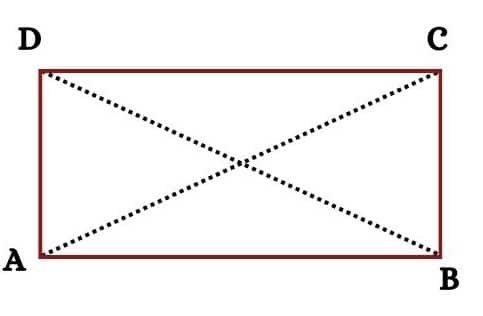
Question 1: If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Answer:
Given: ABCD is a parallelogram with AC=BD.
To prove: ABCD is a rectangle.
Proof: In △ ABC and △ BAD,
BC = AD (Opposite sides of a parallelogram)
AC=BD (Given)
AB=AB (common)
△ ABC $\cong$ △ BAD (By SSS)
$\angle$ABC=$\angle$BAD (CPCT)
and $\angle$ABC+$\angle$BAD=180° (co-interior angles)
2$\angle$BAD=180°
$\angle$BAD=90°
Hence, it is a rectangle.
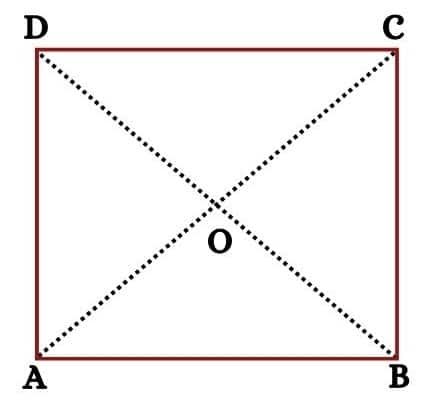
Question 2: Show that the diagonals of a square are equal and bisect each other at right angles.
Answer:
Given: ABCD is a square, i.e. AB=BC=CD=DA.
To prove: the diagonals of a square are equal and bisect each other at right angles, i.e. AC=BD, AO=CO, BO=DO and $\angle$COD=90°
Proof: In △ BAD and △ ABC,
$\angle$BAD=$\angle$ABC (Each 90° )
AD=BC (Given )
AB=AB (common)
△ BAD $\cong$ △ ABC (By SAS)
BD=AC (CPCT)
In △ AOB and △ COD,
$\angle$ OAB= $\angle$ OCD (Alternate angles)
AB=CD (Given )
$\angle$ OBA= $\angle$ ODC (Alternate angles)
△ AOB $\cong$ △ COD (By AAS)
AO=OC ,BO=OD (CPCT)
In △ AOB and △ AOD,
OB=OD (proved above)
AB=AD (Given )
OA=OA (COMMON)
△ AOB $\cong$ △ AOD (By SSS)
$\angle$ AOB= $\angle$ AOD (CPCT)
$\angle$ AOB+ $\angle$ AOD = 180°
2. $\angle$ AOB = 180°
$\angle$ AOB = 90°
Hence, the diagonals of a square are equal and bisect each other at right angles.
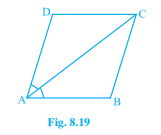
Question 3: (i) Diagonal AC of a parallelogram ABCD bisects $\angle$A (see Fig. 8.19 ). Show that it bisects $\angle$C also.
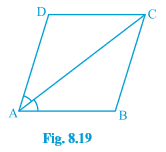
Answer:
Given: $\angle$ DAC= $\angle$ BAC ................1
$\angle$ DAC= $\angle$ BCA.................2 (Alternate angles)
$\angle$ BAC= $\angle$ ACD .................3 (Alternate angles)
From equations 1,2, and 3, we get
$\angle$ ACD= $\angle$ BCA...................4
Hence, diagonal AC bisects angle C also.
Question 3: (ii) Diagonal AC of a parallelogram ABCD bisects $\angle$A (see Fig. 8.19 ). Show that ABCD is a rhombus.
Answer:
Given: $\angle$ DAC= $\angle$ BAC ................1
$\angle$ DAC= $\angle$ BCA.................2 (Alternate angles)
$\angle$ BAC= $\angle$ ACD .................3 (Alternate angles)
From equations 1,2, and 3, we get
$\angle$ ACD= $\angle$ BCA...................4
From 2 and 4, we get
$\angle$ ACD= $\angle$ DAC
In △ ADC,
$\angle$ ACD= $\angle$ DAC (proved above )
AD=DC (In a triangle, sides opposite to equal angles are equal)
A parallelogram whose adjacent sides are equal is a rhombus.
Thus, ABCD is a rhombus.
Question 4: (i) ABCD is a rectangle in which diagonal AC bisects $\angle$A as well as $\angle$C . Show that: ABCD is a square.
Answer:
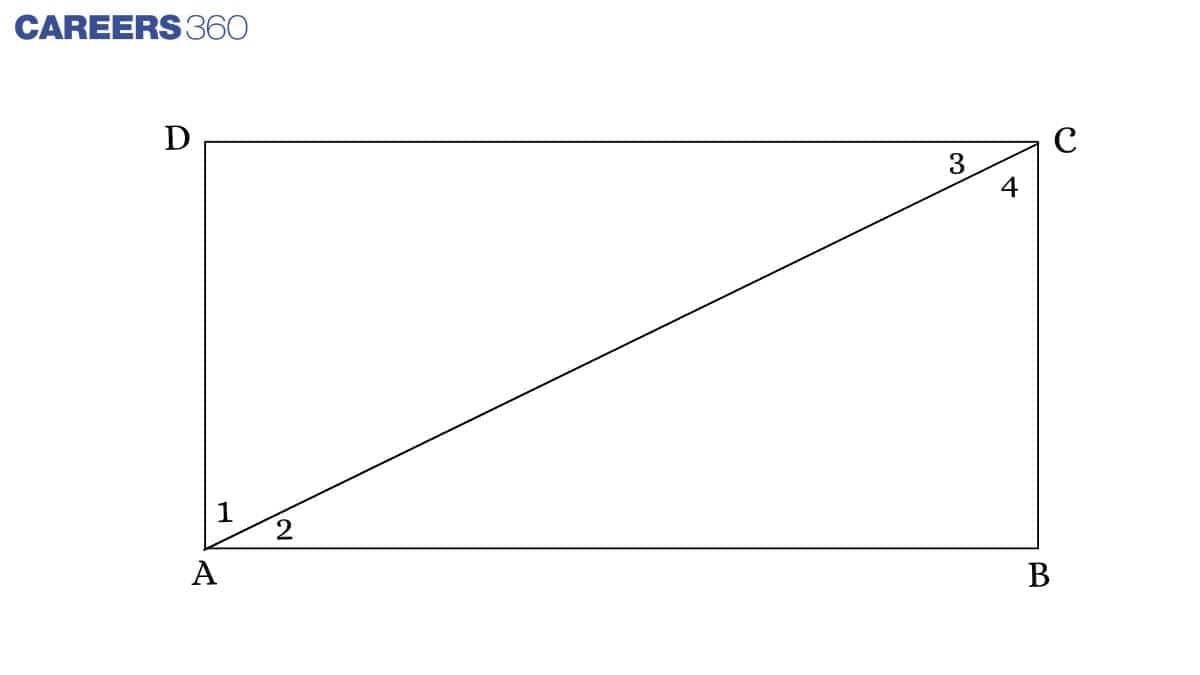
Given: ABCD is a rectangle with AB=CD and BC=AD $\angle$ 1= $\angle$ 2 and $\angle$ 3= $\angle$ 4.
To prove: ABCD is a square.
Proof : $\angle$ 1= $\angle$ 4 .............1(alternate angles)
$\angle$ 3= $\angle$ 4 ................2(given )
From 1 and 2, $\angle$ 1= $\angle$ 3.....................................3
In △ ADC,
$\angle$ 1= $\angle$ 3 (from 3 )
DC=AD (In a triangle, sides opposite to equal angles are equal )
A rectangle whose adjacent sides are equal is a square.
Hence, ABCD is a square.
Question 4: (ii) ABCD is a rectangle in which diagonal AC bisects $\angle$A as well as $\angle$C. Show that: Diagonal BD bisects $\angle$B as well as $\angle$D.
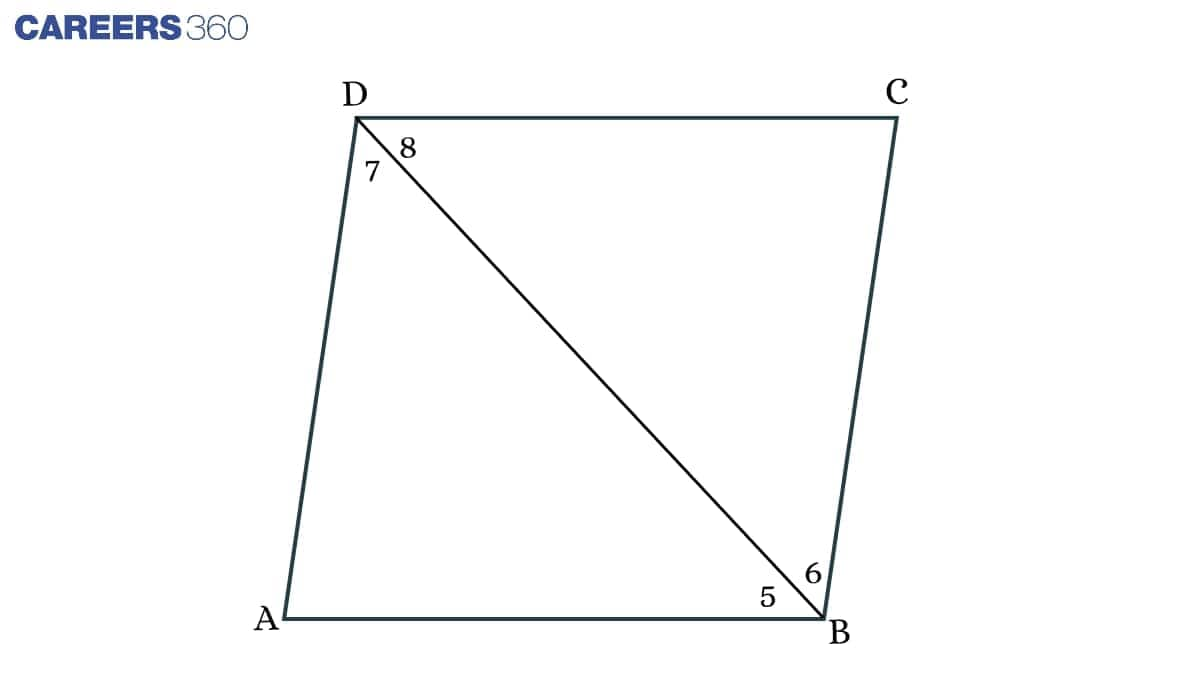
Answer:
In △ ADB,
AD = AB (ABCD is a square)
$\angle$ 5= $\angle$ 7.................1(angles opposite to equal sides are equal )
$\angle$ 5= $\angle$ 8.................2 (alternate angles)
From 1 and 2, we have
$\angle$ 7= $\angle$ 8.................3
and $\angle$ 7 = $\angle$ 6.................4(alternate angles)
From 1 and 4, we get
$\angle$ 5= $\angle$ 6.................5
Hence, from 3 and 5, diagonal BD bisects angles B as well as angle D.
Question 5: (i) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.20 ). Show that: ΔAPD$\cong$ΔCQB
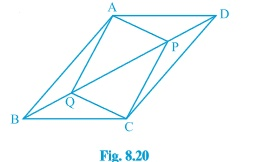
Answer:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: ΔAPD$\cong$ΔCQB
Proof :
In ΔAPDandΔCQB,
DP=BQ (Given )
$\angle$ ADP= $\angle$ CBQ (alternate angles)
AD=BC (opposite sides of a parallelogram)
ΔAPD$\cong$ΔCQB (By SAS)
Question 5: (ii) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.20 ). Show that: AP=CQ
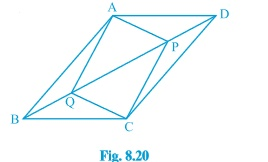
Answer:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: AP=CQ
Proof:
In ΔAPDandΔCQB,
DP=BQ (Given )
$\angle$ ADP= $\angle$ CBQ (alternate angles)
AD=BC (opposite sides of a parallelogram)
ΔAPD$\cong$ΔCQB (By SAS)
AP=CQ (CPCT)
Question 5: (iii) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.20 ). Show that: ΔAQB$\cong$ΔCPD
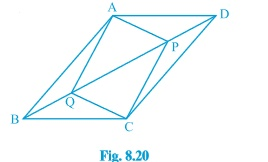
Answer:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: ΔAQB$\cong$ΔCPD
Proof :
In ΔAQB and ΔCPD,
DP=BQ (Given )
$\angle$ ABQ= $\angle$ CDP (alternate angles)
AB=CD (opposite sides of a parallelogram)
ΔAQB$\cong$ΔCPD (By SAS)
Question 5: (iv) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.20 ). Show that: AQ=CP
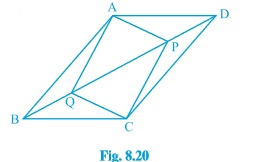
Answer:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: AQ=CP
Proof:
In ΔAQB and ΔCPD,
DP=BQ (Given )
$\angle$ ABQ= $\angle$ CDP (alternate angles)
AB=CD (opposite sides of a parallelogram)
ΔAQB$\cong$ΔCPD (By SAS)
AQ=CP (CPCT)
Question 5: (v) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.20 ). Show that: APCQ is a parallelogram
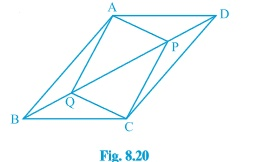
Answer:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: APCQ is a parallelogram
Proof:
In ΔAPD and ΔCQB,
DP=BQ (Given )
$\angle$ ADP= $\angle$ CBQ (alternate angles)
AD=BC (opposite sides of a parallelogram)
ΔAPD$\cong$ΔCQB (By SAS)
AP=CQ (CPCT)...............................................................(1)
Also,
In ΔAQB and ΔCPD,
DP=BQ (Given )
$\angle$ ABQ= $\angle$ CDP (alternate angles)
AB=CD (opposite sides of a parallelogram)
ΔAQB$\cong$ΔCPD (By SAS)
AQ=CP (CPCT)........................................(2)
From equations 1 and 2, we get
AP=CQ
AQ=CP
Thus, opposite sides of quadrilateral APCQ are equal so APCQ is a parallelogram.
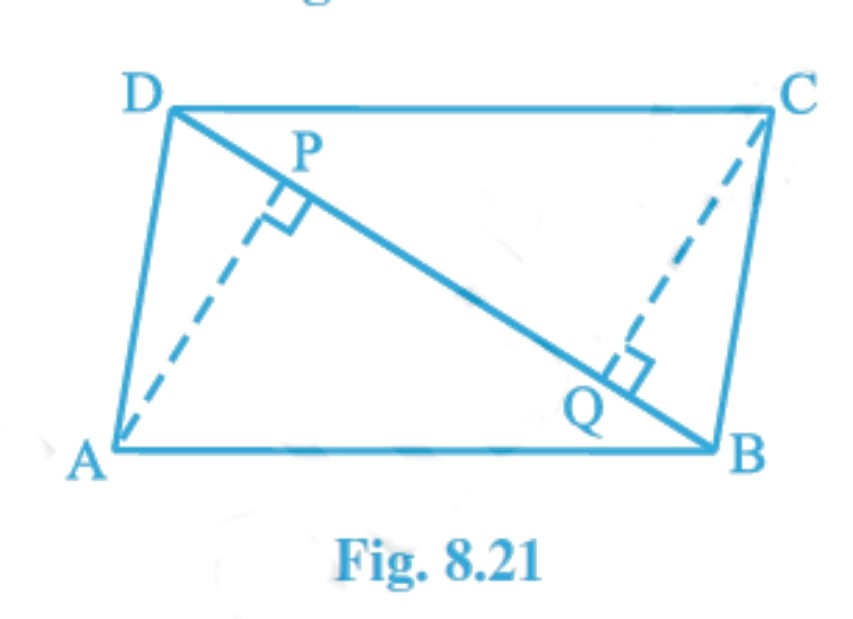
Question 6: (i) ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21 ). Show that ΔAPB$\cong$ΔCQD
Answer:
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD.
To prove: ΔAPB$\cong$ΔCQD
Proof: In ΔAPB and ΔCQD,
$\angle$ APB= $\angle$ CQD (Each 90° )
$\angle$ ABP= $\angle$ CDQ (Alternate angles)
AB=CD (Opposite sides of a parallelogram )
Thus, ΔAPB$\cong$ΔCQD (By SAS)
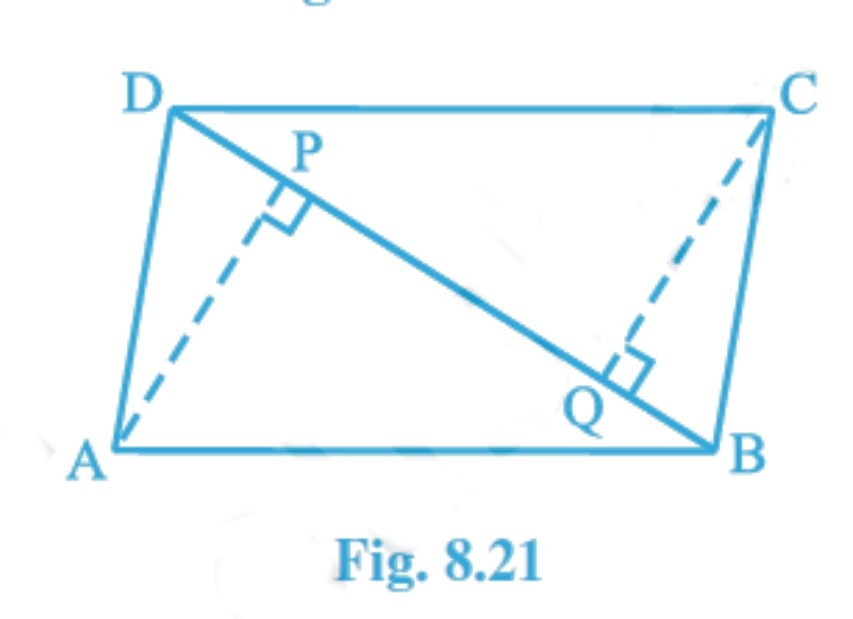
Question 6: (ii) ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21 ). Show that AP=CQ
Answer:
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD.
To prove: AP=CQ
Proof: In ΔAPB and ΔCQD,
$\angle$ APB= $\angle$ CQD (Each 90° )
$\angle$ ABP= $\angle$ CDQ (Alternate angles)
AB=CD (Opposite sides of a parallelogram )
Thus, ΔAPB$\cong$ΔCQD (By SAS)
AP=CQ (CPCT)
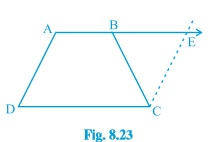
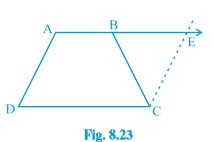
Question 7: (i) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.23 ). Show that $\angle$A=$\angle$B
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Answer:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: $\angle$A=$\angle$B
Proof: Let $\angle$ A be $\angle$ 1, $\angle$ ABC be $\angle$ 2, $\angle$ EBC be $\angle$ 3, $\angle$ BEC be $\angle$ 4.
In AECD,
AE||DC (Given)
AD||CE (By construction)
Hence, AECD is a parallelogram.
AD=CE...............(1)(opposite sides of a parallelogram)
AD=BC.................(2)(Given)
From equations 1 and 2, we get,
CE=BC
In △ BCE,
$\angle$3=$\angle$4 .................3 (opposite angles of equal sides)
$\angle$2+$\angle$3=180° ...................4(linear pairs)
$\angle$1+$\angle$4=180° .....................5(Co-interior angles)
From 4 and 5, we get
$\angle$2+$\angle$3=$\angle$1+$\angle$4
∴$\angle$2=$\angle$1→$\angle$B=$\angle$A (Since, $\angle$3=$\angle$4 )
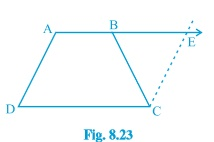
Question 7: (ii) ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that $\angle$C=$\angle$D
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Answer:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: $\angle$C=$\angle$D
Proof: Let $\angle$ A be $\angle$ 1, $\angle$ ABC be $\angle$ 2, $\angle$ EBC be $\angle$ 3, $\angle$ BEC be $\angle$ 4.
$\angle$1+$\angle$D=180° (Co-interior angles)
$\angle$2+$\angle$C=180° (Co-interior angles)
∴$\angle$1+$\angle$D=$\angle$2+$\angle$C
Thus, $\angle$C=$\angle$D (Since , $\angle$1=$\angle$2 )
Question 7: (iii) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.23 ). Show that ΔABC$\cong$ΔBAD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Answer:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: ΔABC$\cong$ΔBAD
Proof: In ΔABC and ΔBAD ,
BC=AD (Given )
AB=AB (Common )
$\angle$ABC=$\angle$BAD (proved in (i) )
Thus, ΔABC$\cong$ΔBAD (By SAS rule)
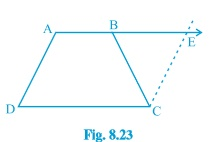
Question 7: (iv) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.23 ). Show that diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E]
Answer:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: diagonal AC = diagonal BD
Proof: In ΔABC and ΔBAD,
BC=AD (Given )
AB=AB (Common )
$\angle$ABC = $\angle$BAD (proved in (i) )
Thus, ΔABC$\cong$ΔBAD (By SAS rule)
diagonal AC = diagonal BD (CPCT)
| Quadrilaterals Class 9 Question Answers: Exercise: 8.2 Page Number: 113-114 Total Questions: 6 |
Answer:
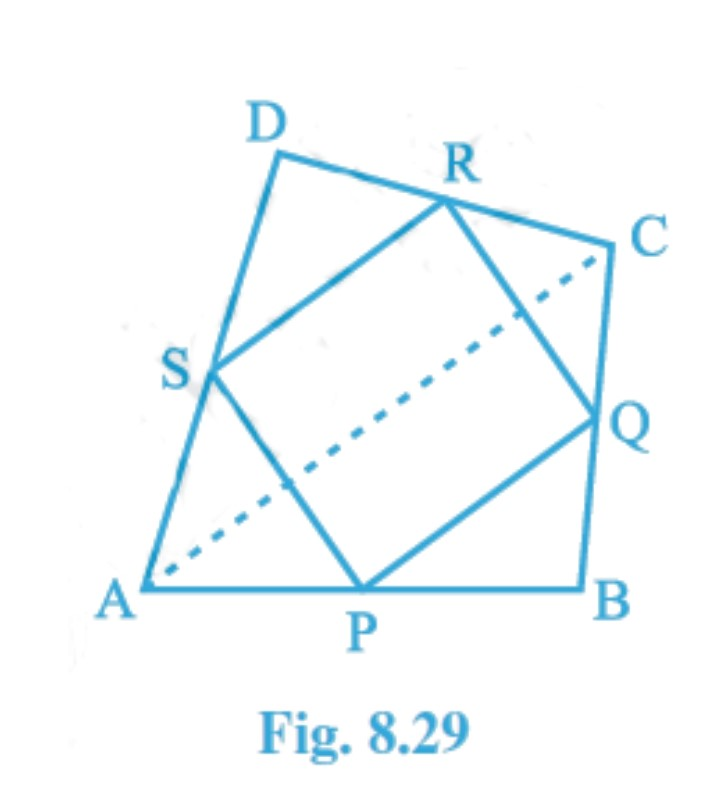
Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig. 8.29 ). AC is a diagonal.
To prove :
SR∥AC and SR=12AC
Proof: In △ ACD,
S is the midpoint of DA. (Given)
R is the midpoint of DC. (Given)
By the midpoint theorem,
SR∥AC and SR=12AC
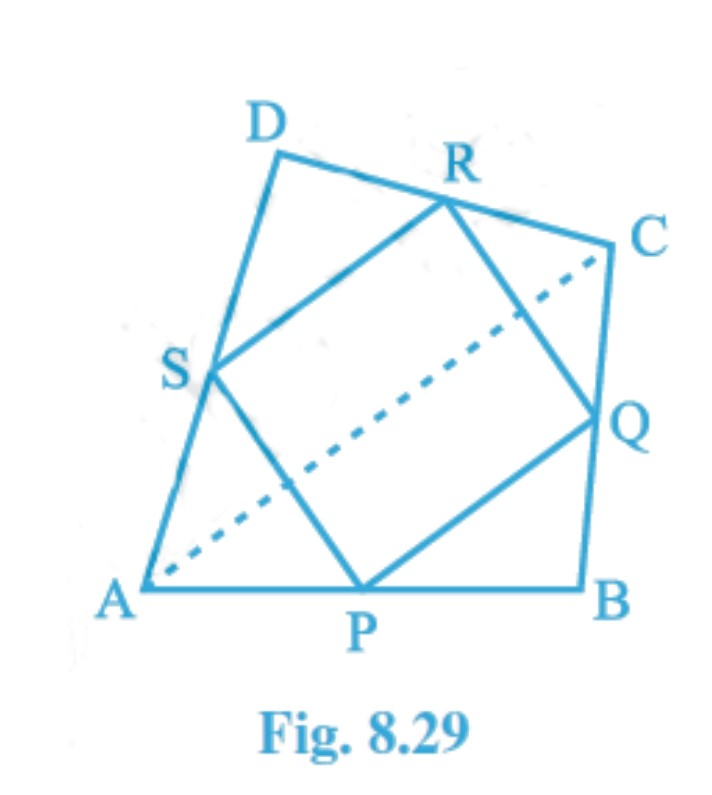
Question 1: (ii) ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29 ). AC is a diagonal. Show that : PQ=SR
Answer:
Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig. 8.29 ). AC is a diagonal.
To prove: PQ=SR
Proof: In △ ACD,
S is the midpoint of DA. (Given)
R is the midpoint of DC. (Given)
By the mid-point theorem,
SR∥AC and SR=12AC ...................................(1)
In △ ABC,
P is the midpoint of AB. (Given)
Q is the midpoint of BC. (Given)
By the mid-point theorem,
PQ∥AC and PQ=12AC .................................(2)
From equations 1 and 2, we get
PQ∥SR and PQ=SR=12AC
Thus, PQ=SR
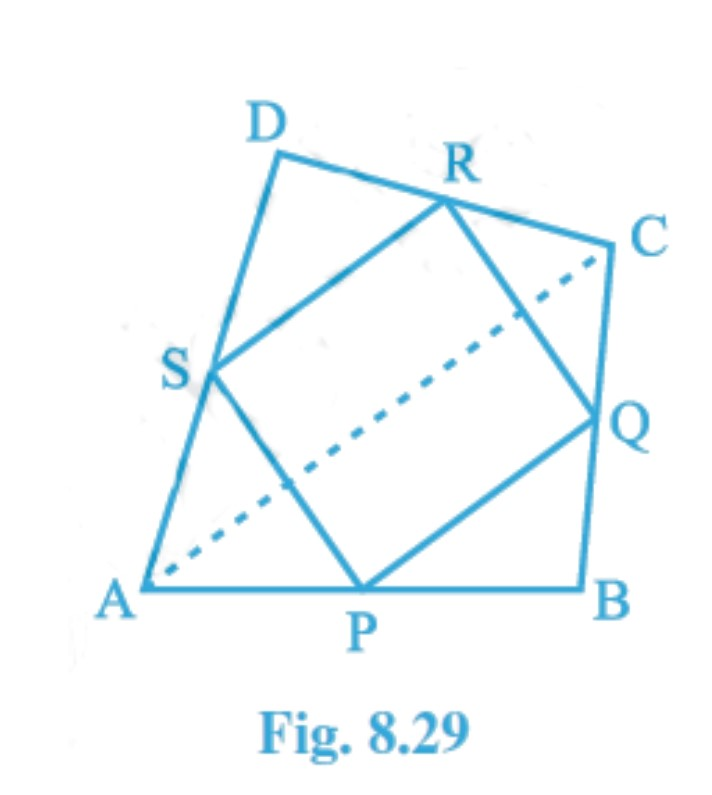
Answer:
Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig. 8.29 ). AC is a diagonal.
To prove: PQRS is a parallelogram.
Proof: In PQRS,
Since,
PQ∥SR and PQ=SR.
So, PQRS is a parallelogram.
Answer:
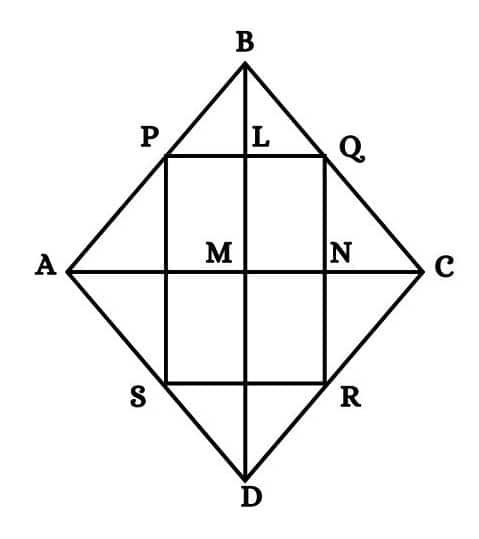
Given: ABCD is a rhombus in which P, Q, R and S are mid-points of the sides AB, BC, CD, and DA, AC and BD are diagonals.
To prove: the quadrilateral PQRS is a rectangle.
Proof: In △ ACD,
S is the midpoint of DA. (Given)
R is the midpoint of DC. (Given)
By the midpoint theorem,
SR∥AC and SR=12AC ...................................(1)
In △ ABC,
P is the midpoint of AB. (Given)
Q is the midpoint of BC. (Given)
By the mid-point theorem,
PQ∥AC and PQ=12AC .................................(2)
From 1 and 2, we get
PQ∥SR and PQ=SR=12AC
Thus, PQ=SR and PQ∥SR
So, the quadrilateral PQRS is a parallelogram.
Similarly, in △ BCD,
Q is the midpoint of BC. (Given)
R is the midpoint of DC. (Given)
By the midpoint theorem,
QR∥BD
So, QN || LM ...........(5)
LQ || MN ..........(6) (Since, PQ || AC)
From 5 and 6, we get
LMPQ is a parallelogram.
Hence, $\angle$ LMN= $\angle$ LQN (opposite angles of the parallelogram)
But, $\angle$ LMN = 90° (Diagonals of a rhombus are perpendicular)
so, $\angle$ LQN=90°
Thus, a parallelogram whose one angle is a right angle is a rectangle.
Hence, PQRS is a rectangle.
Answer:
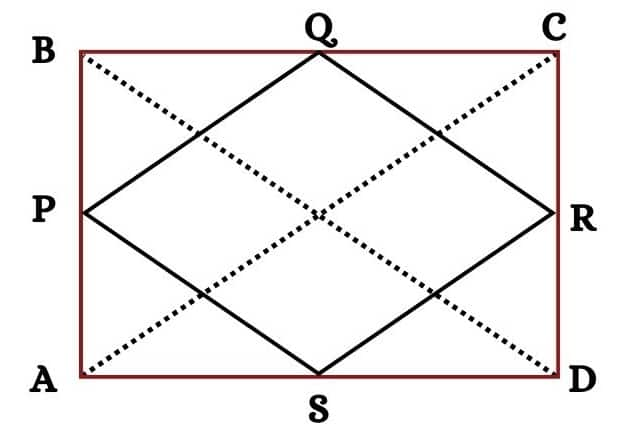
Given: ABCD is a rectangle and P, Q, R, and S are mid-points of the sides AB, BC, CD and DA, respectively.
To prove: the quadrilateral PQRS is a rhombus.
Proof :
In △ ACD,
S is the midpoint of DA. (Given)
R is the midpoint of DC. (Given)
By the midpoint theorem,
SR∥AC and SR=12AC ...................................(1)
In △ ABC,
P is the midpoint of AB. (Given)
Q is the midpoint of BC. (Given)
By the midpoint theorem,
PQ∥AC and PQ=12AC .................................(2)
From 1 and 2, we get
PQ∥SR and PQ=SR=12AC
Thus, PQ=SR and PQ∥SR
So, the quadrilateral PQRS is a parallelogram.
Similarly, in △ BCD,
Q is the midpoint of BC. (Given)
R is the midpoint of DC. (Given)
By the midpoint theorem,
QR∥BD and QR=12BD ...................(5)
AC = BD.......................(6)(diagonals )
From 2, 5 and 6, we get
PQ=QR
Thus, a parallelogram whose adjacent sides are equal is a rhombus. Hence, PQRS is a rhombus.
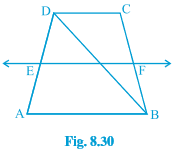
Answer:
Given: ABCD is a trapezium in which AB∥DC, BD is a diagonal, and E is the mid-point of AD. A line is drawn through E parallel to AB, intersecting BC at F (see Fig. 8.30 ).
To prove: F is the mid-point of BC.
In △ ABD,
E is the midpoint of AD. (Given)
EG || AB (Given)
By the converse of the midpoint theorem,
G is the midpoint of BD.
In △ BCD,
G is the midpoint of BD. (Proved above)
FG || DC (Given)
By the converse of the midpoint theorem,
F is the midpoint of BC.
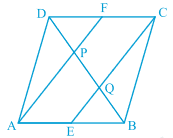
Answer:
Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively
To prove: the line segments AF and EC trisect the diagonal BD.
Proof: In quadrilateral ABCD,
AB=CD (Given)
12AB=12CD
⇒AE=CF (E and F are midpoints of AB and CD)
In quadrilateral AECF,
AE=CF (Given)
AE || CF (Opposite sides of a parallelogram)
Hence, AECF is a parallelogram.
In △ DCQ,
F is the midpoint of DC. (given )
FP || CQ (AECF is a parallelogram)
By the converse of the midpoint theorem,
P is the midpoint of DQ.
DP= PQ....................(1)
Similarly,
In △ ABP,
E is the midpoint of AB. (given )
EQ || AP (AECF is a parallelogram)
By the converse of the midpoint theorem,
Q is the midpoint of PB.
OQ= QB....................(2)
From 1 and 2, we have
DP = PQ = QB.
Hence, the line segments AF and EC trisect the diagonal BD.
Answer:
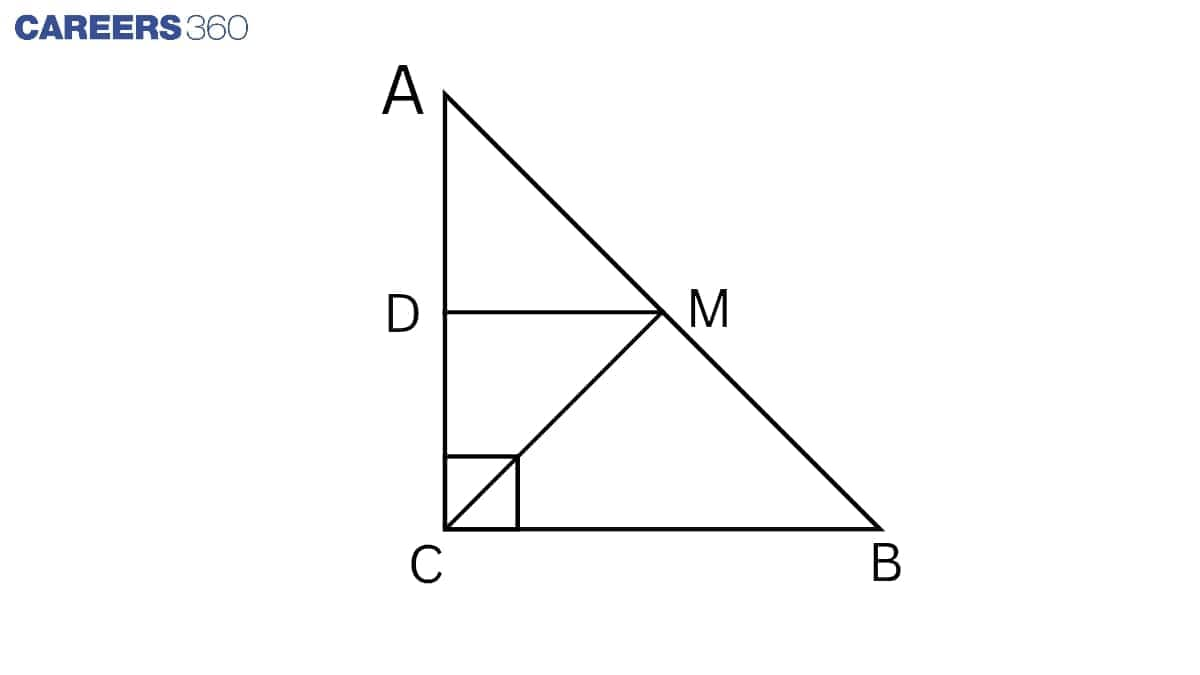
Given: ABC is a triangle right angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.
To prove :D is the midpoint of AC.
Proof: In △ ABC,
M is mid point of AB. (Given)
DM || BC (Given)
By the converse of mid point theorem,
D is the mid point of AC.
Question 6: (ii) ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC
Answer:
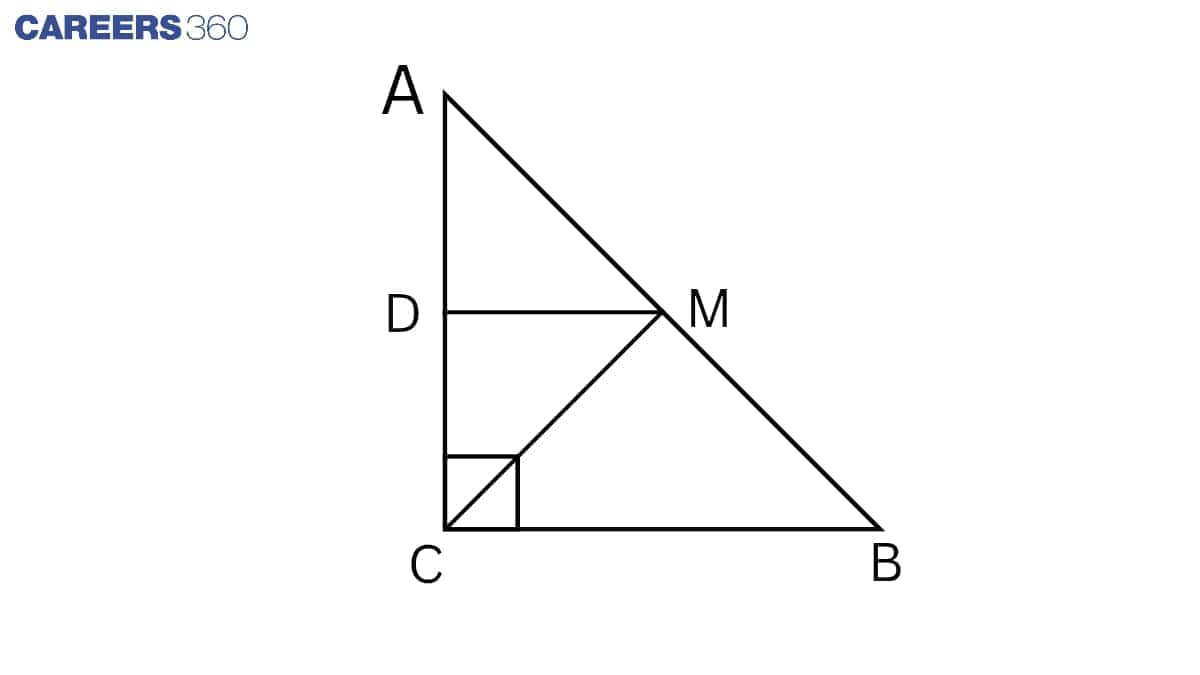
Given: ABC is a triangle right angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.
To prove: MD⊥AC
Proof : $\angle$ ADM = $\angle$ ACB (Corresponding angles)
$\angle$ ADM= 90° ( $\angle$ ACB = 90° )
Hence, MD⊥AC.
Question 6: (iii) ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM=MA=12AB
Answer:
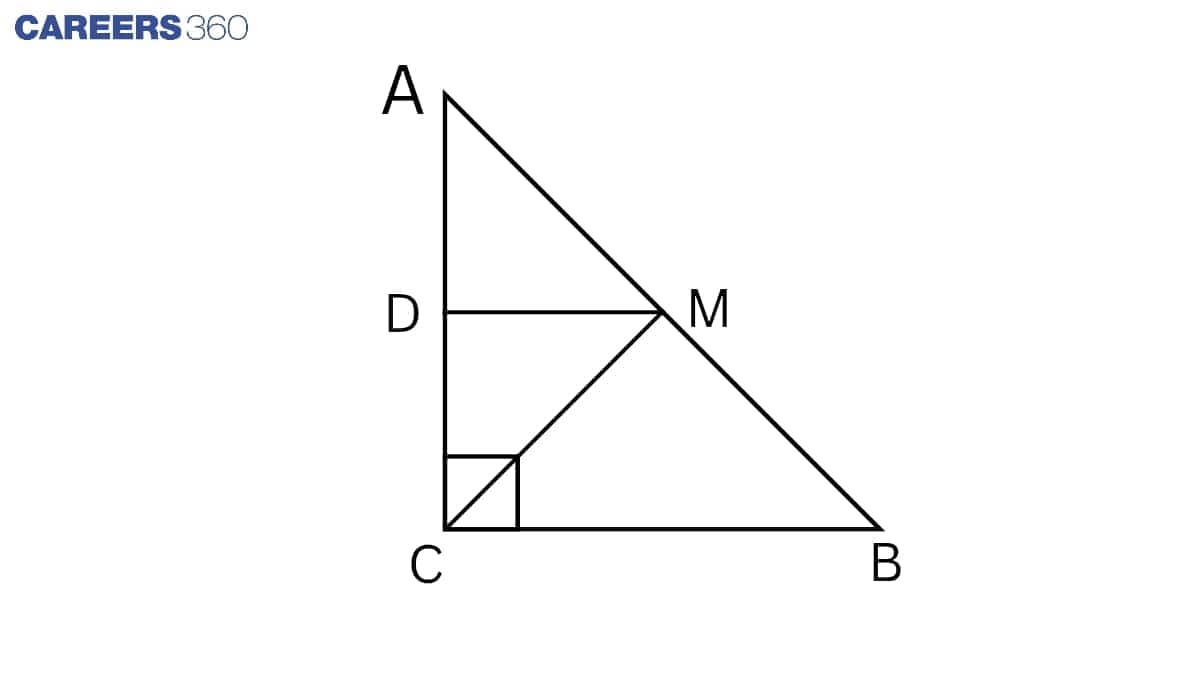
Given: ABC is a triangle right angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.
To prove: CM=MA=12AB
Proof: In △ ABC,
M is the midpoint of AB. (Given)
DM || BC (Given)
By the converse of the midpoint theorem,
D is the midpoint of AC i.e. AD = DC.
In △ AMD and △ CMD,
AD = DC (proved above)
$\angle$ ADM = $\angle$ CDM (Each right angle)
DM = DM (Common)
△ AMD $\cong$ △ CMD (By SAS)
AM = CM (CPCT)
But, AM=12AB
Hence, CM=MA=12AB.
Quadrilaterals Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Quadrilaterals Class 9 Maths Chapter 8 are provided in the link below.
Class 11 Maths NCERT Chapter 8: Extra Question
Question: In quadrilateral ABCD, AB is parallel to CD, and $\angle$A = 70°, $\angle$D = 110°. Find $\angle$B and $\angle$C.
Answer:
We know that, in a quadrilateral with one pair of opposite sides parallel, adjacent angles on the same side of a transversal are supplementary.
Now, by the angle sum property of a quadrilateral:
$\angle$A+$\angle$B+$\angle$C+$\angle$D = 360°
70°+\angle B+\angle C$ + 110° = 360°
$\angle$B + $\angle$C = 180°
As we are given that AB is parallel to CD
So, $\angle$B = $\angle$C (alternate interior angles)
Therefore, $\angle$B=$\angle$C = 90°
Quadrilaterals Class 9 Chapter 8: Topics
Students will explore the following topics in NCERT Class 9 Maths Chapter 8 Quadrilaterals:
- Properties of a Parallelogram
- The Mid-point Theorem
- Summary
Quadrilaterals Class 9 NCERT Solutions: Important Formulae And Points
Quadrilateral
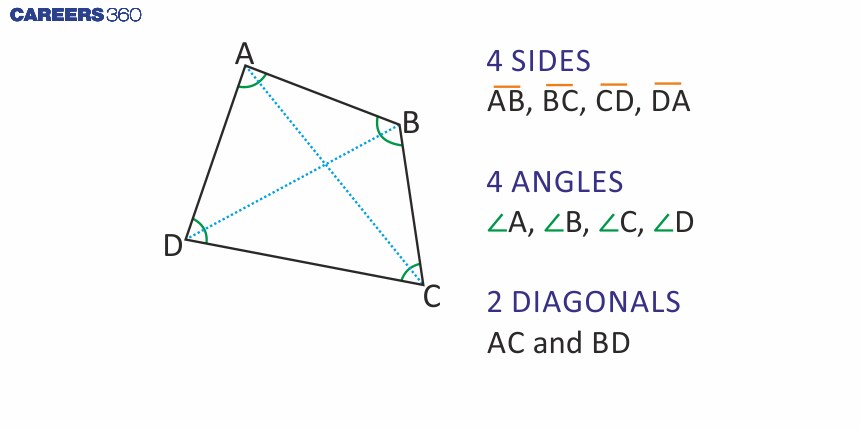
Quadrilaterals are an important part of geometry, having four sides. There are some important quadrilaterals, i.e. squares, rectangles, trapezium, rhombus, and parallelograms. A quadrilateral also has four angles, four vertices, 12 edges, and two diagonals.
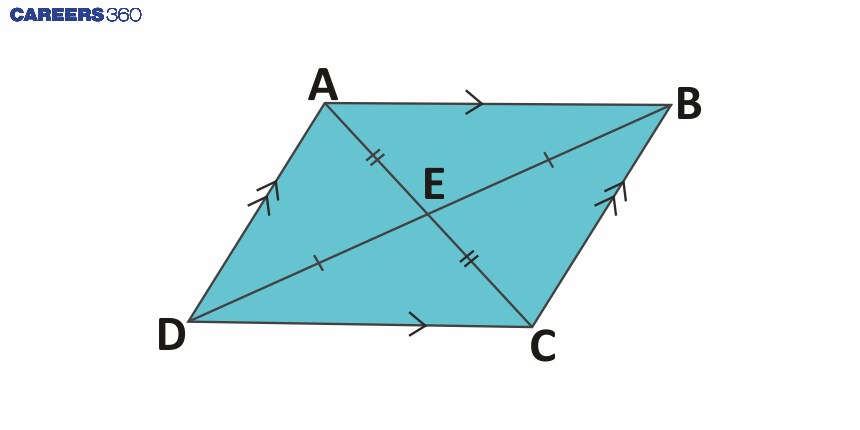
Parallelogram
-
A diagonal of a parallelogram divides it into two congruent triangles.
-
In a parallelogram, the diagonals bisect each other.
-
In a parallelogram, opposite angles are equal.
-
In a parallelogram, opposite sides are equal.
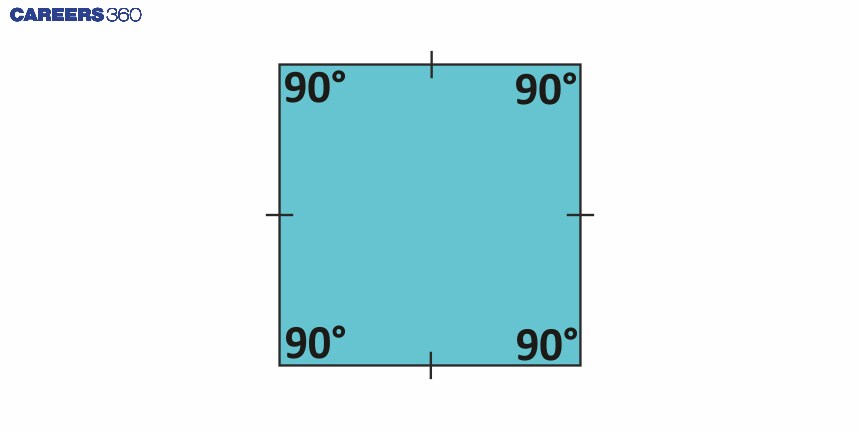
Square
-
Diagonals of a square bisect each other at right angles and are equal, and vice versa.
Triangle
-
A line through the midpoint of a side of a triangle parallel to another side bisects the third side (Midpoint theorem).
-
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and equal to half the third side.
Parallelogram Angle Bisectors
-
In a parallelogram, the bisectors of any two consecutive angles intersect at a right angle.
-
If a diagonal of a parallelogram bisects one of the angles of a parallelogram, it also bisects the second angle.
Rectangle
-
The angle bisectors of a parallelogram form a rectangle.
-
Each of the four angles of a rectangle is a right angle.
Rhombus
-
The diagonals of a rhombus are perpendicular to each other.
Perimeter of a Quadrilateral
|
Quadrilateral Name |
Perimeter |
|
Square |
4 × Side |
|
Rectangle |
2 × (Length + Breadth) |
|
Parallelogram |
2 × (Base + Side) |
|
Rhombus |
4 × Side |
|
Kite |
2 × (Sum of the unequal adjacent pairs) |
Area of Quadrilaterals
|
Quadrilateral Name |
Area |
|
Area of a Parallelogram |
Base × Height |
|
Area of a Rectangle |
Length × Breadth |
|
Area of a Square |
Side × Side |
|
Area of a Rhombus |
$\frac{1}{2}$ × Diagonal$_1$ × Diagonal$_2$ |
|
Area of a Kite |
$\frac{1}{2}$ × Diagonal$_1$ × Diagonal$_2$ |
Approach to Solve Questions of Quadrilaterals Class 9
Using these approaches, students can tackle the Quadrilaterals Class 9 Chapter 8 Question Answers with greater confidence.
1. Learn basic properties of quadrilaterals: Any shape that comprises four sides proves to be a quadrilateral, and its total internal angles create a 360-degree circle.
2. Identify types of quadrilaterals: The study of special parallelograms and rhombuses, rectangles, and trapeziums, along with their specific properties, should be studied.
3. Use angle sum property: Solving for unknown angles requires using the formula, which calculates that $\angle$A + $\angle$B + $\angle$C + $\angle$D = 360.
4. Apply properties of parallelograms: The shape contains equal and parallel sides, which have identical opposite angles.
5. Use diagonal properties: The diagonals of rectangles and rhombuses hold either equal measurement lengths or bisect each other, providing valuable tools for question verification.
6. Solve reasoning-based and proof questions: Develop proof statements together with supporting reasons to show whether a particular quadrilateral qualifies as a parallelogram.
NCERT Solutions For Class 9 Mathematics - Chapter Wise
For students' preparation, Careers360 has gathered all Class 9 Maths NCERT solutions here for quick and convenient access.
Also, read,
- NCERT Notes Class 9 Maths Chapter 8 Quadrilaterals
- NCERT Exemplar Solutions for Class 9 Maths Chapter 8 Quadrilaterals
NCERT Books and NCERT Syllabus
Given below are some useful links for NCERT books and the NCERT syllabus for class 9:
Frequently Asked Questions (FAQs)
Q: Where can I download NCERT Solutions for Quadrilaterals?
A:
Free downloadable NCERT Quadrilaterals Class 9 solutions PDFs are available on various trusted educational platforms, such as Careers360. Students can find the free downloadable PDF in this article itself.
Q: Why are NCERT Solutions for Chapter 8 useful?
A:
These solutions provide step-by-step proofs of all theorems, solved examples, and exercises with logical reasoning, making it easier for students to understand geometry.
Q: What are the important topics in maths chapter 8 class 9 Quadrilaterals?
A:
Angle sum property of a quadrilateral, properties of the parallelogram, another condition for a quadrilateral to be a parallelogram, and the mid-point theorem are the important topics covered in NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals.
Q: How does the NCERT solutions are helpful ?
A:
NCERT solutions are not only helpful for students if they get stuck while solving NCERT problems, but also it will provide them with new ways to solve the problems. We at Careers360 provide these solutions in a very detailed manner, giving students conceptual clarity.
Q: Which theorems are important to deal with class 9 maths chapter 8 question answer?
A:
Here is the list of theorems that are important for this chapter.
A diagonal of a parallelogram divides it into two congruent triangles.
Opposite sides of a parallelogram are equal.
Opposite angles of a parallelogram are equal.
Diagonals of a parallelogram bisect each other.
A quadrilateral is a parallelogram if opposite sides/angles are equal or if its diagonals bisect each other.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters