NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.1 - Quadrilaterals

Q1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Solution:
Given: ABCD is a parallelogram with AC = BD.
To prove: ABCD is a rectangle.
Proof: In △ ABC and △ BAD,

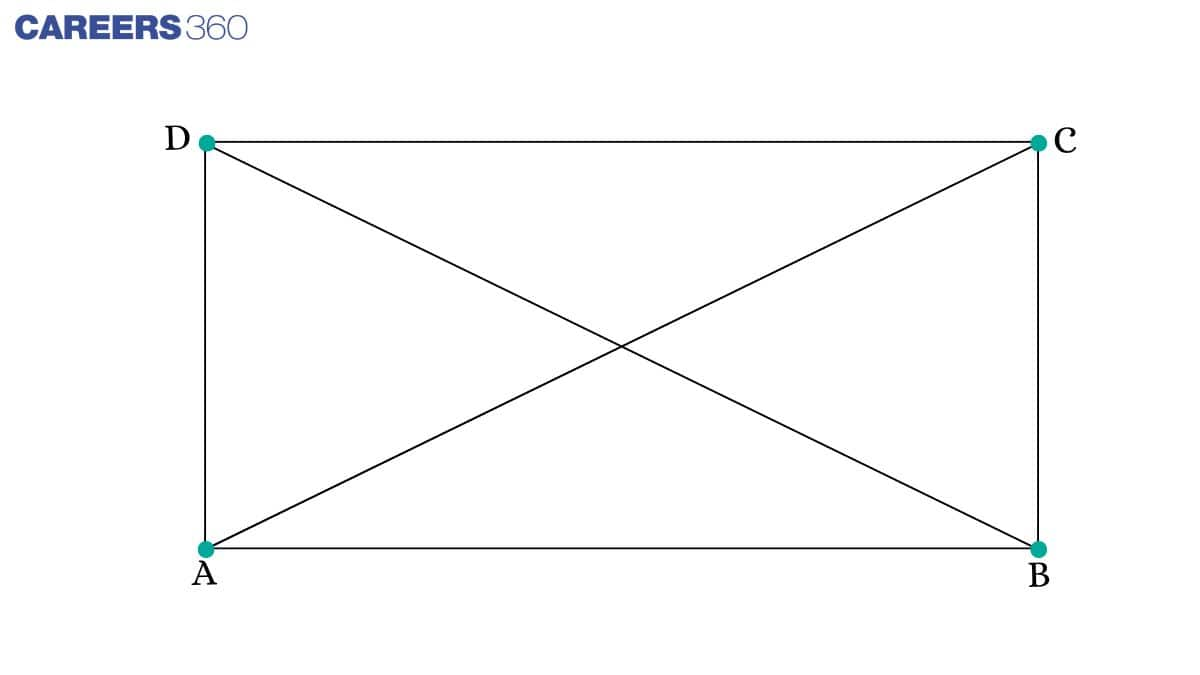
BC = AD (Opposite sides of a parallelogram)
AC = BD (Given)
AB = AB (Common)
△ ABC ≅ △ BAD (By SSS)
∠ABC=∠BAD (CPCT)
And ∠ABC+∠BAD=180∘ (Co - interior angles)
2∠BAD=180∘
∠BAD=90∘
Hence, it is a rectangle.

Q2. Show that the diagonals of a square are equal and bisect each other at right angles.

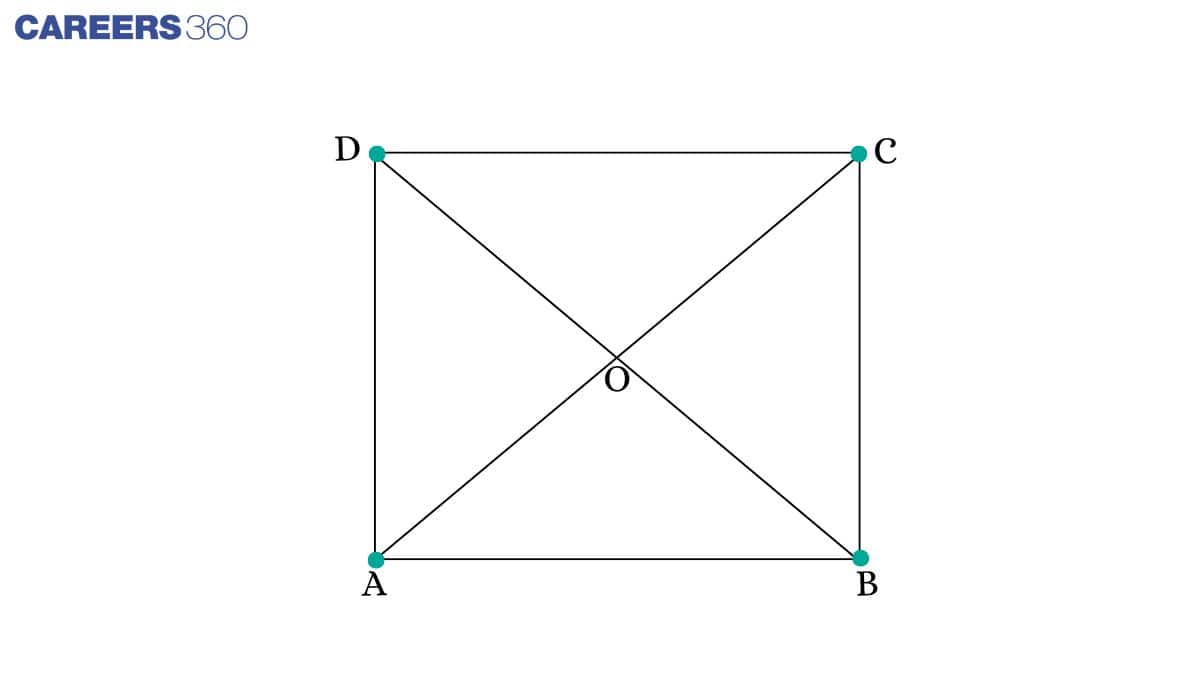
Solution:
Given: ABCD is a square, i.e. AB = BC = CD = DA.
To prove: the diagonals of a square are equal and bisect each other at right angles i.e. AC = BD, AO = CO, BO = DO and ∠COD=90∘
Proof: In △ BAD and △ ABC,
∠BAD=∠ABC (Each 90∘)
AD = BC (Given)
AB = AB (Common)
△ BAD ≅ △ ABC (By SAS)
BD = AC (CPCT)
In △ AOB and △ COD,
∠ OAB= ∠ OCD (Alternate angles)
AB = CD (Given)
∠ OBA= ∠ ODC (Alternate angles)
△ AOB ≅ △ COD (By AAS)
AO = OC, BO = OD (CPCT)
In △ AOB and △ AOD,
OB = OD (proved above)
AB = AD (Given)
OA = OA (Common)
△ AOB ≅ △ AOD (By SSS)
∠ AOB = ∠ AOD (CPCT)
∠ AOB+ ∠ AOD = 180∘
2∠ AOB = 180∘
∠ AOB = 90∘
Hence, the diagonals of a square are equal and bisect each other at right angles.

Q3 (i) Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19 ). Show that it bisects ∠C also.

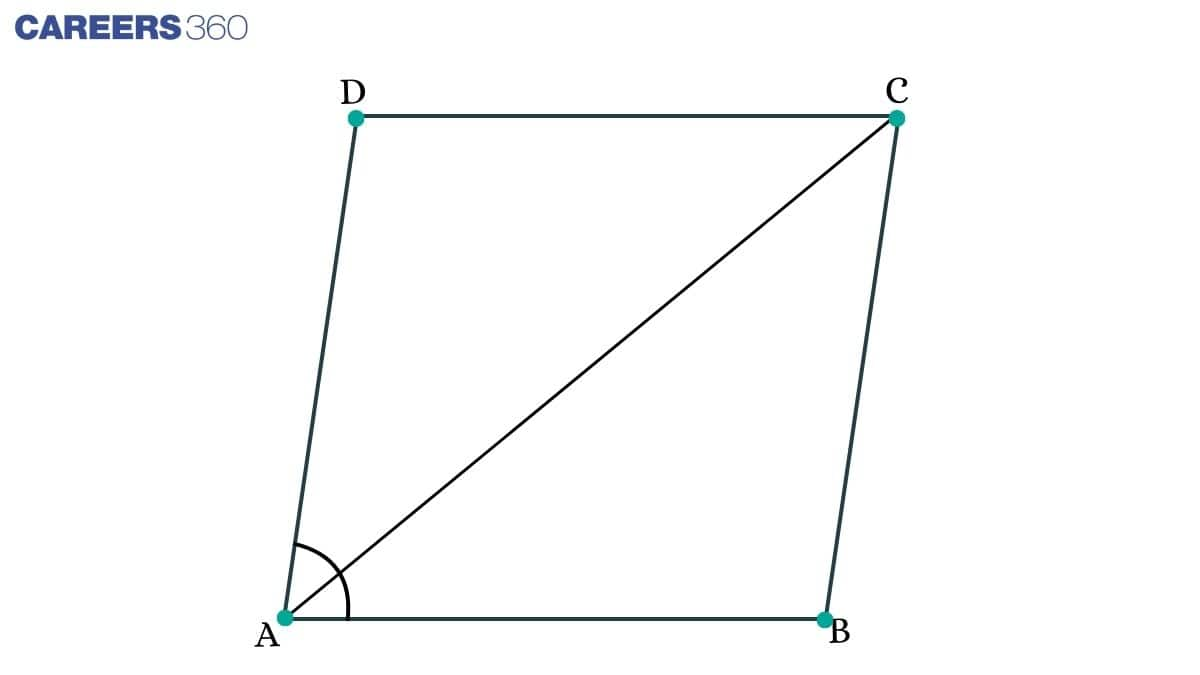
Solution:
Given: ∠ DAC= ∠ BAC ..........(1)
∠ DAC= ∠ BCA.............(2) (Alternate angles)
∠ BAC= ∠ ACD .............(3) (Alternate angles)
From equations (1), (2) and (3), we get
∠ ACD= ∠ BCA...............(4)
Hence, diagonal AC bisect angle C also.

Q3 (ii) Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19 ). Show that ABCD is a rhombus.

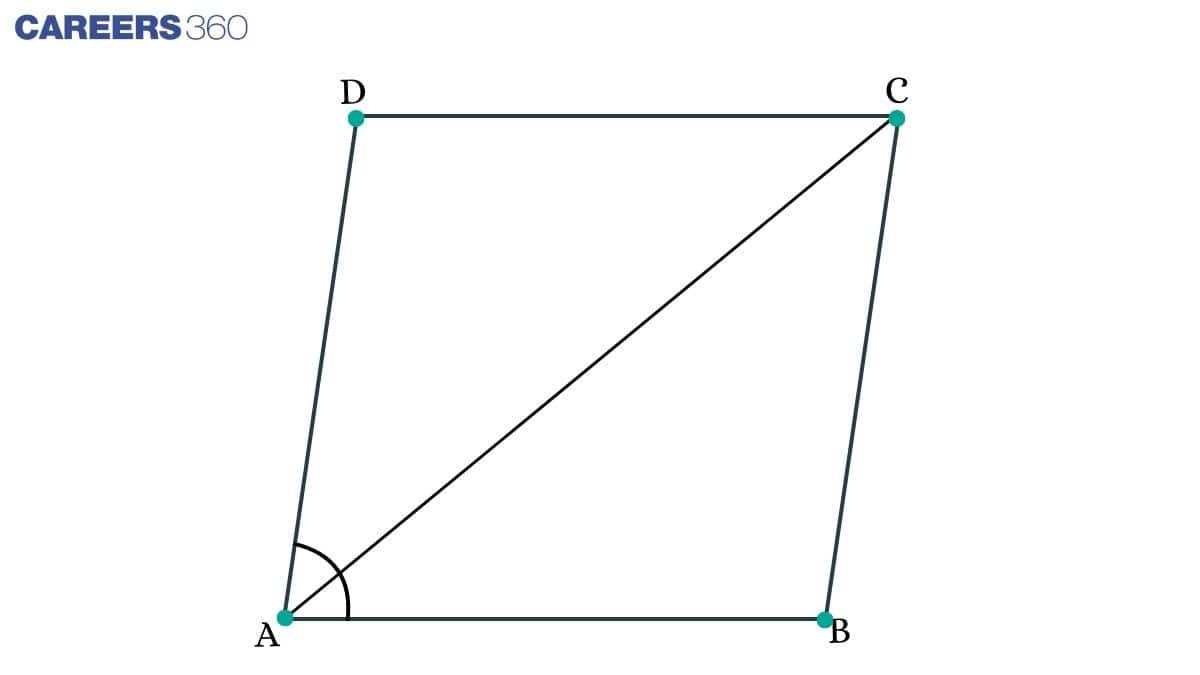
Solution:
Given: ∠ DAC= ∠ BAC .............(1)
∠ DAC= ∠ BCA..............(2) (Alternate angles)
∠ BAC= ∠ ACD ..............(3) (Alternate angles)
From equations (1), (2), and (3), we get
∠ ACD= ∠ BCA..............(4)
From 2 and 4, we get
∠ ACD= ∠ DAC
In △ ADC,
∠ ACD= ∠ DAC (proved above)
AD = DC (In a triangle, sides opposite to equal angles are equal)
A parallelogram whose adjacent sides are equal is a rhombus.

Thus, ABCD is a rhombus.

Q4 (i) ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: ABCD is a square

Solution:

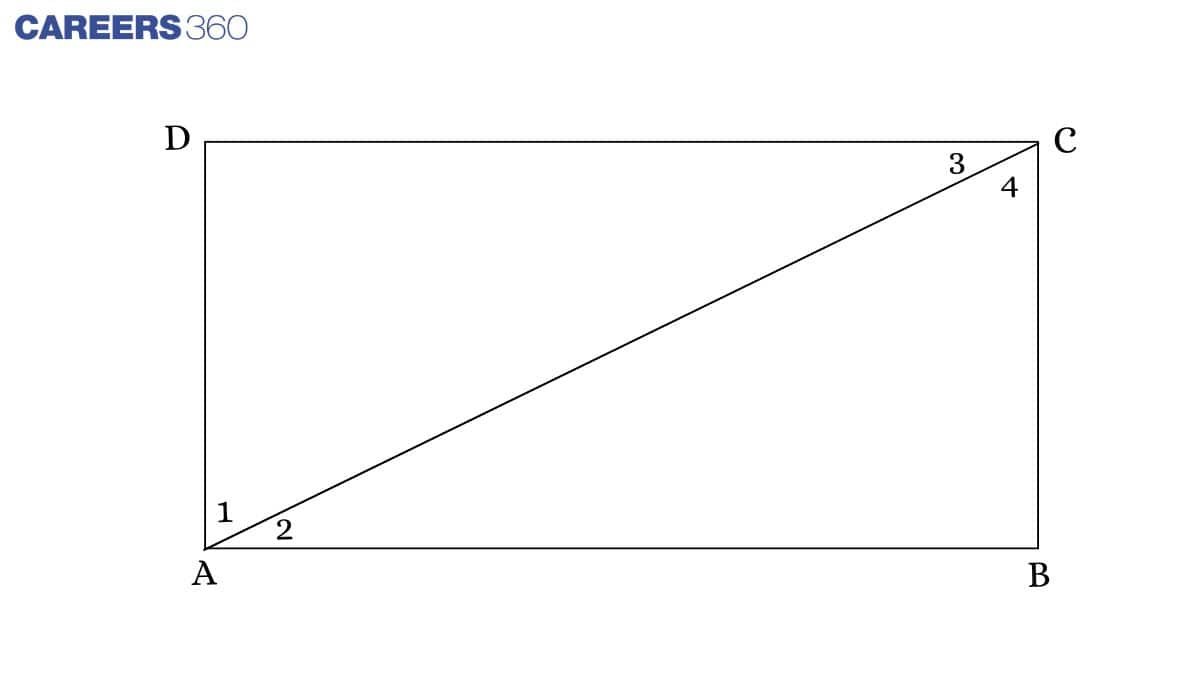
Given: ABCD is a rectangle with AB=CD and BC=AD ∠ 1= ∠ 2 and ∠ 3= ∠ 4.
To prove: ABCD is a square.
Proof : ∠ 1= ∠ 4 ............(1)(Alternate angles)
∠ 3= ∠ 4 ..............(2)(Given )
From 1 and 2, ∠ 1= ∠ 3.......................(3)
In △ ADC,
∠ 1= ∠ 3 (From 3 )
DC = AD (In a triangle, sides opposite to equal angles are equal)
A rectangle whose adjacent sides are equal is a square.
Hence, ABCD is a square.

Q4 (ii) ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: diagonal BD bisects ∠B as well as ∠D .

Solution:

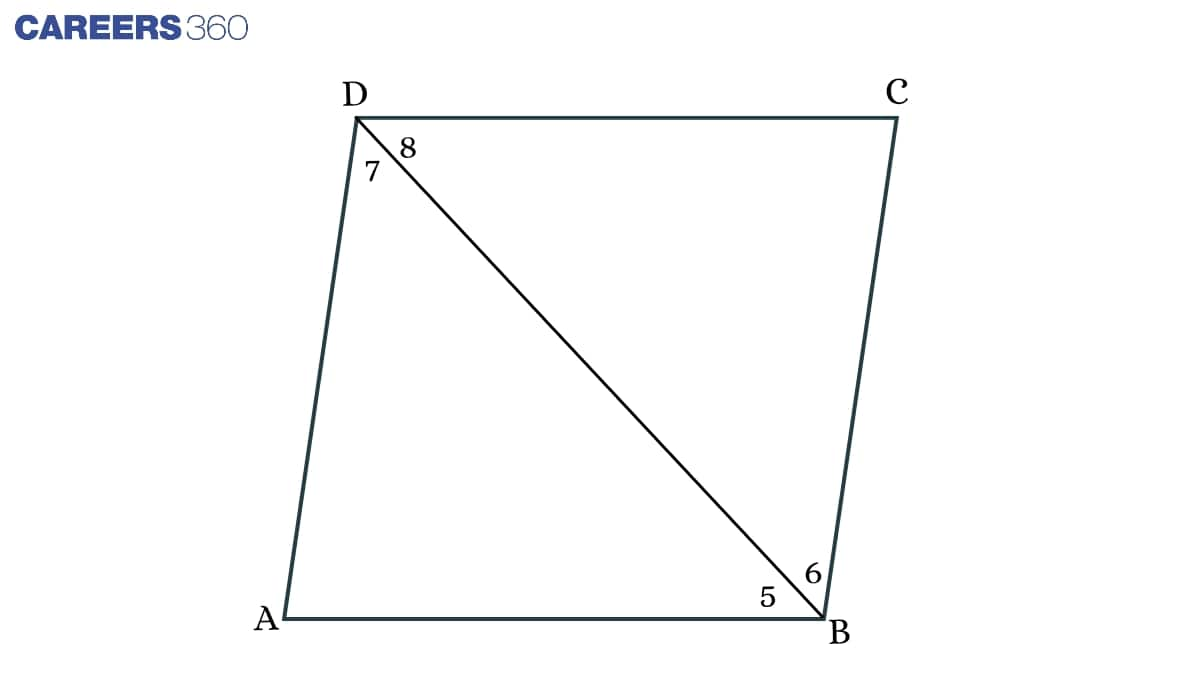
In △ ADB,
AD = AB (ABCD is a square)
∠ 5= ∠ 7...............(1) (Angles opposite to equal sides are equal)
∠ 5= ∠ 8...............(2) (Alternate angles)
From (1) and (2), we have
∠ 7= ∠ 8.............(3)
And ∠ 7 = ∠ 6.................4(Alternate angles)
From (1) and (4), we get
∠ 5= ∠ 6..............(5)
Hence, from 3 and 5, diagonal BD bisects angles B as well as angle D.

Q5 (i) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.12 ). Show that: ΔAPD≅ΔCQB

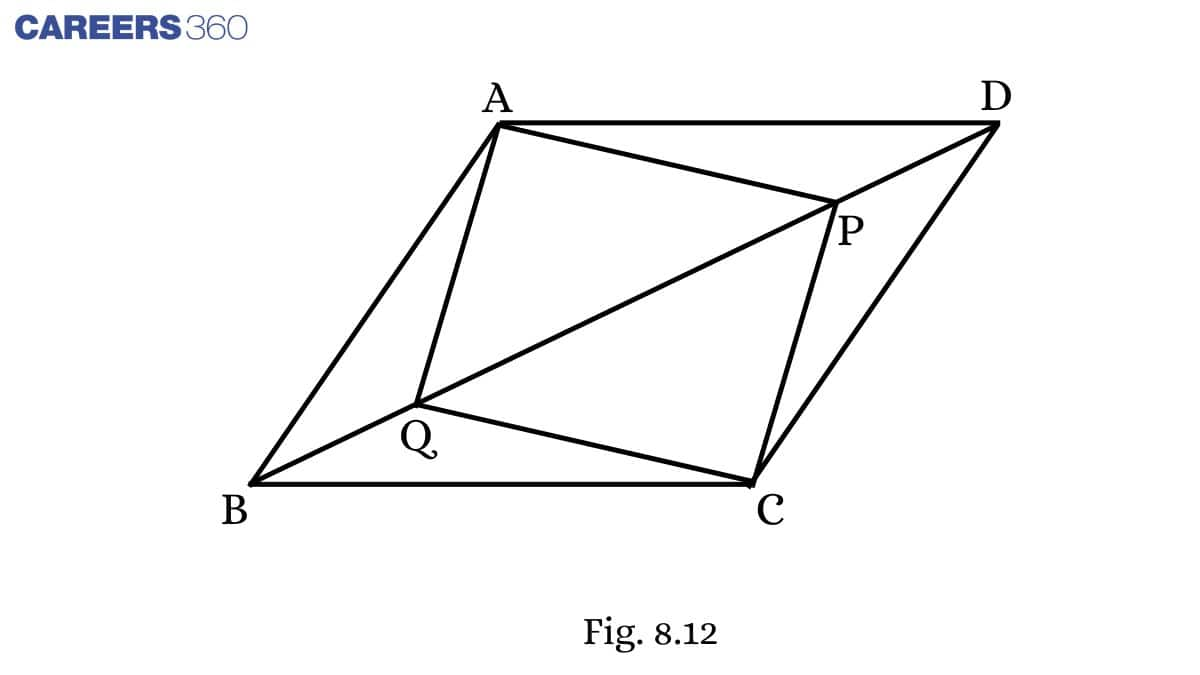
Solution:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove : ΔAPD≅ΔCQB
Proof:
In ΔAPDandΔCQB,
DP=BQ (Given)
∠ ADP= ∠ CBQ (Alternate angles)
AD = BC (Opposite sides of a parallelogram)
ΔAPD≅ΔCQB (By SAS)

Q5 (ii) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.12 ). Show that: AP=CQ

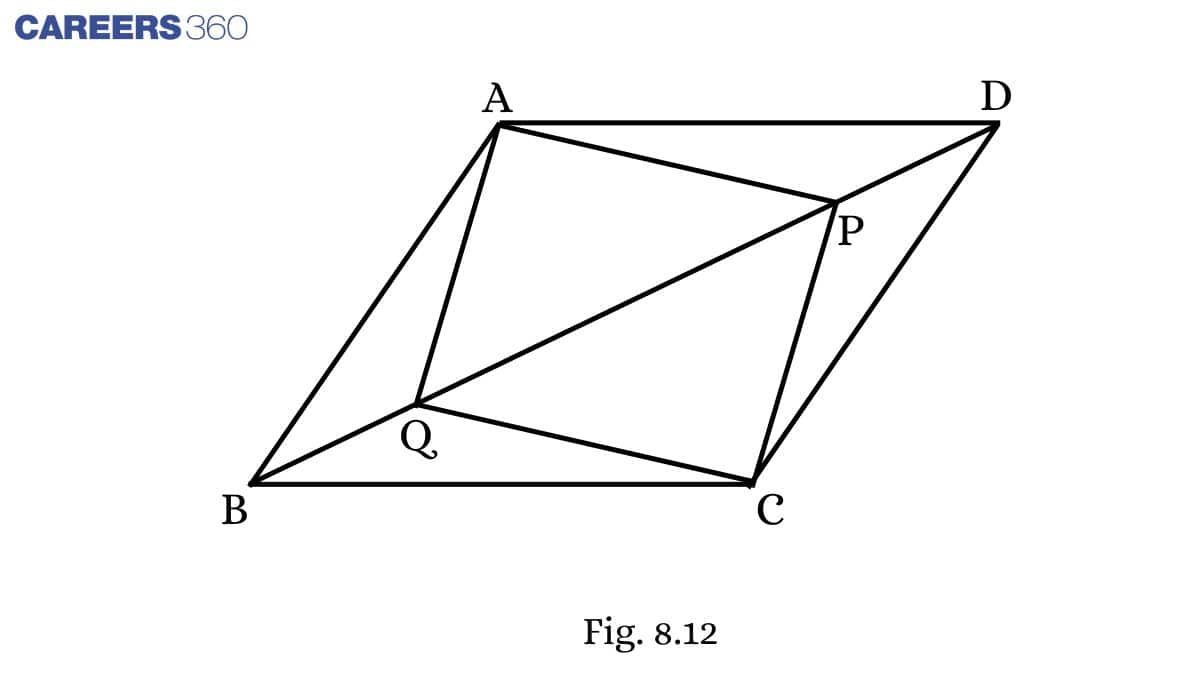
Solution:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: AP=CQ
Proof:
In ΔAPDandΔCQB,
DP=BQ (Given)
∠ ADP= ∠ CBQ (Alternate angles)
AD = BC (Opposite sides of a parallelogram)
ΔAPD≅ΔCQB (By SAS)
AP=CQ (CPCT)

Q5 (iii) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.12 ). Show that: ΔAQB≅ΔCPD

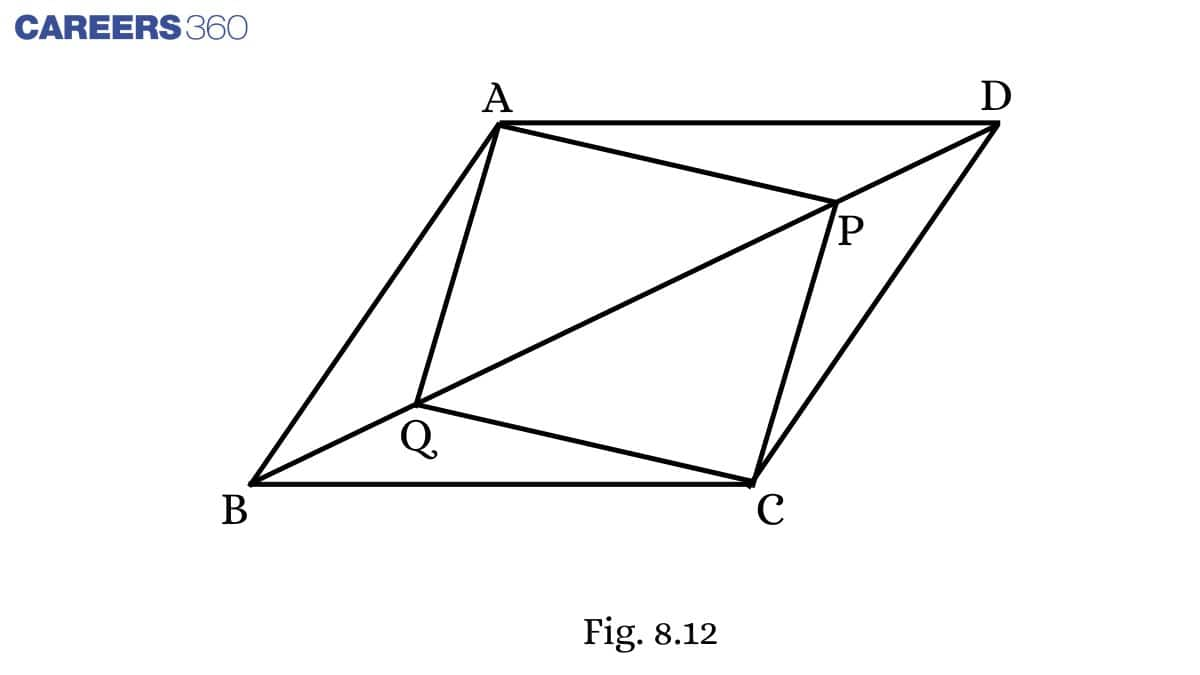
Solution:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: ΔAQB≅ΔCPD
Proof:
In ΔAQBandΔCPD,
DP = BQ (Given)
∠ ABQ= ∠ CDP (Alternate angles)
AB = CD (Opposite sides of a parallelogram)
ΔAQB≅ΔCPD (By SAS)

Q5 (iv) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.12 ). Show that: AQ=CP

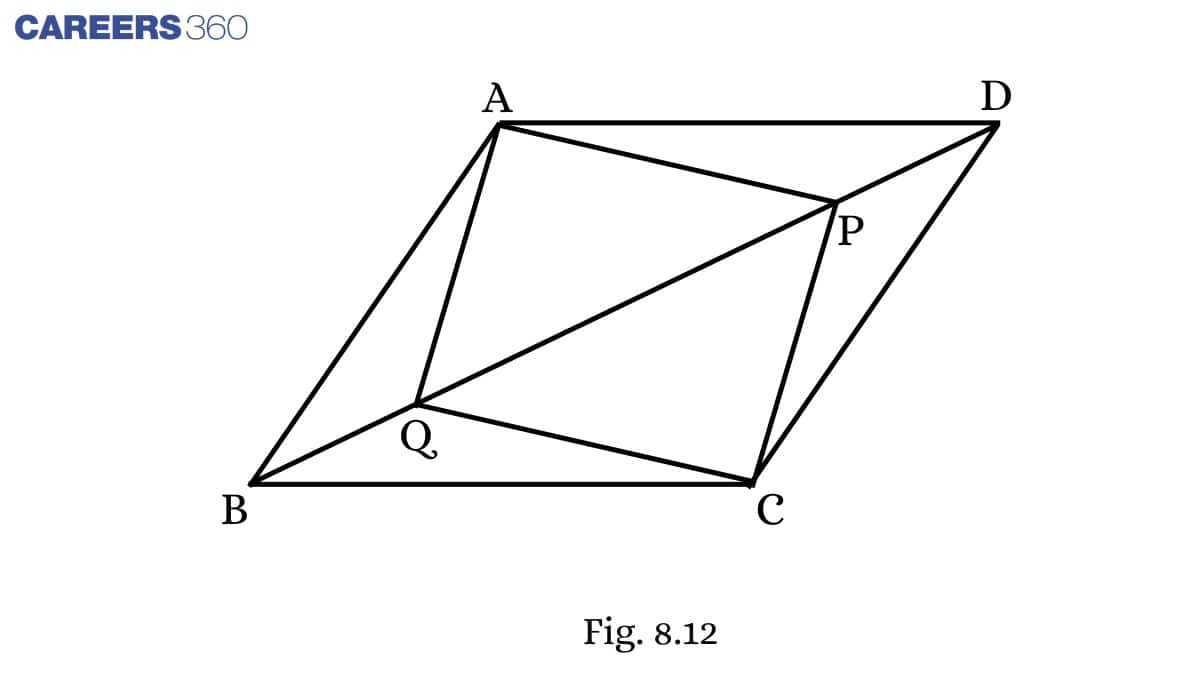
Solution:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: AQ=CP
Proof:
In ΔAQBandΔCPD,
DP = BQ (Given)
∠ ABQ= ∠ CDP (Alternate angles)
AB = CD (Opposite sides of a parallelogram)
ΔAQB≅ΔCPD (By SAS)
AQ=CP (CPCT)

Q5 (v) In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ (see Fig. 8.12 ). Show that: APCQ is a parallelogram

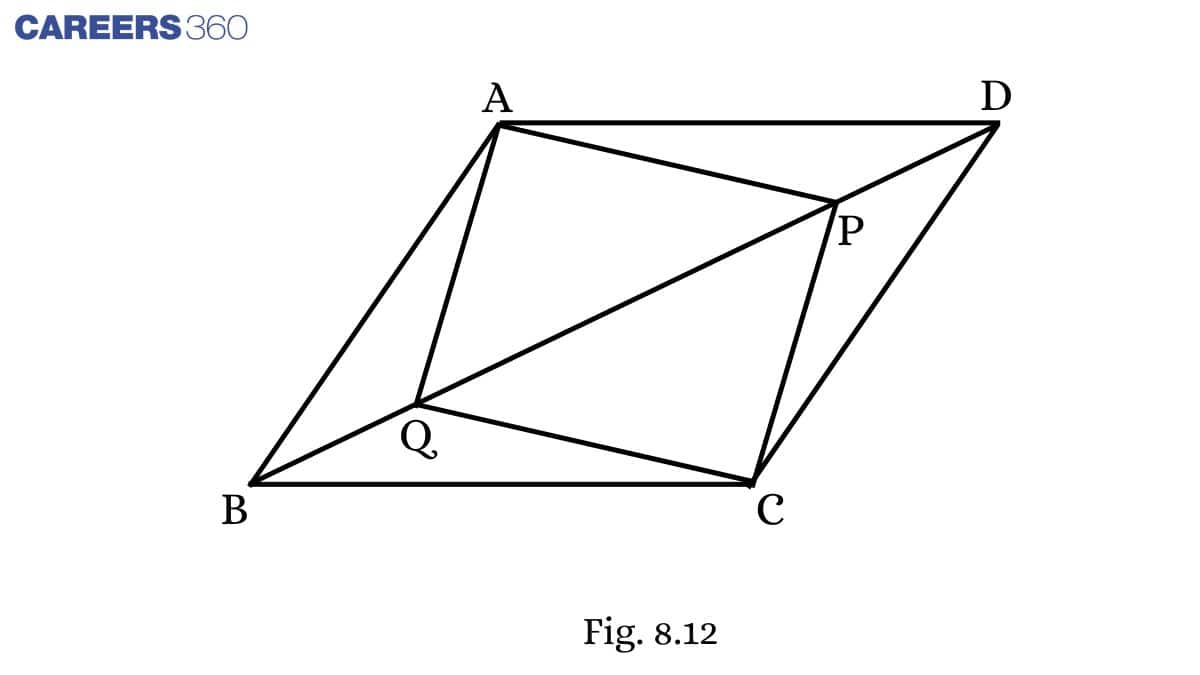
Solution:
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ.
To prove: APCQ is a parallelogram
Proof:
In ΔAPDandΔCQB,
DP = BQ (Given)
∠ ADP= ∠ CBQ (alternate angles)
AD = BC (Opposite sides of a parallelogram)
ΔAPD≅ΔCQB (By SAS)
AP=CQ (CPCT)..............(1)
Also,
In ΔAQBandΔCPD,
DP = BQ (Given)
∠ ABQ= ∠ CDP (Alternate angles)
AB = CD (Opposite sides of a parallelogram)
ΔAQB≅ΔCPD (By SAS)
AQ=CP (CPCT)................(2)
From equations 1 and 2, we get
AP=CQ
AQ=CP
Thus, opposite sides of quadrilateral APCQ are equal, so APCQ is a parallelogram.

Q6 (i) ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.13 ). Show that ΔAPB≅ΔCQD

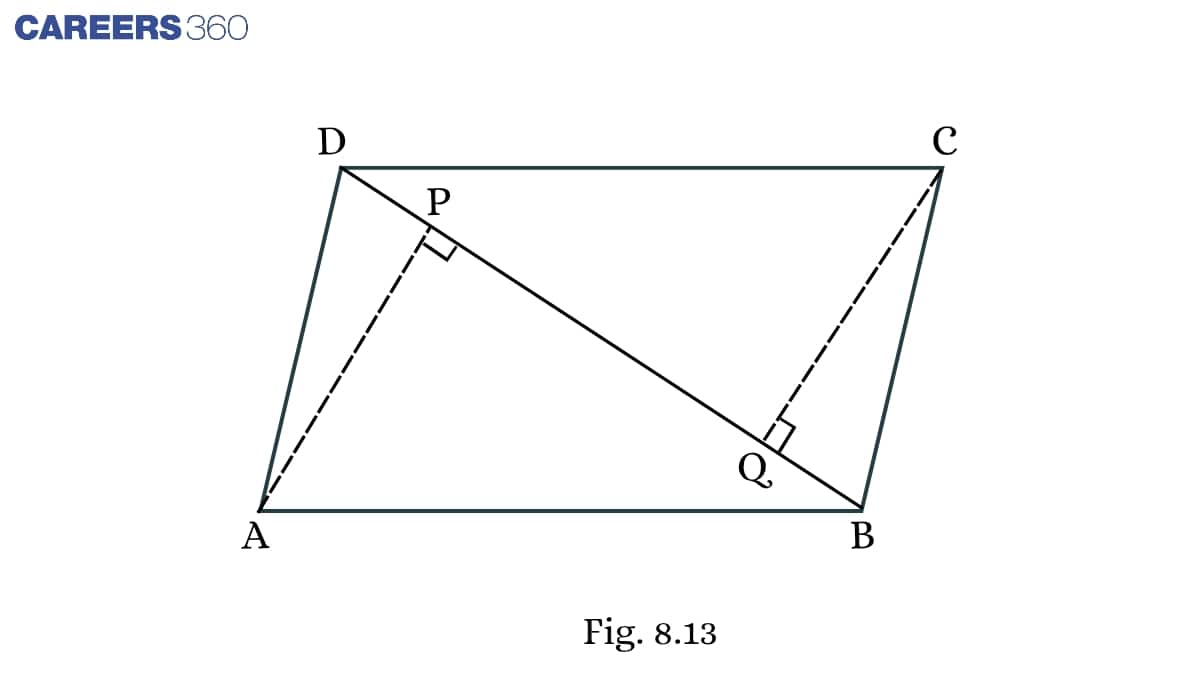
Solution:
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD.
To prove: ΔAPB≅ΔCQD
Proof: In ΔAPBandΔCQD,
∠ APB= ∠ CQD (Each 90∘)
∠ ABP= ∠ CDQ (Alternate angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAPB≅ΔCQD (By SAS)

Q6 (ii) ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.13 ). Show that AP=CQ

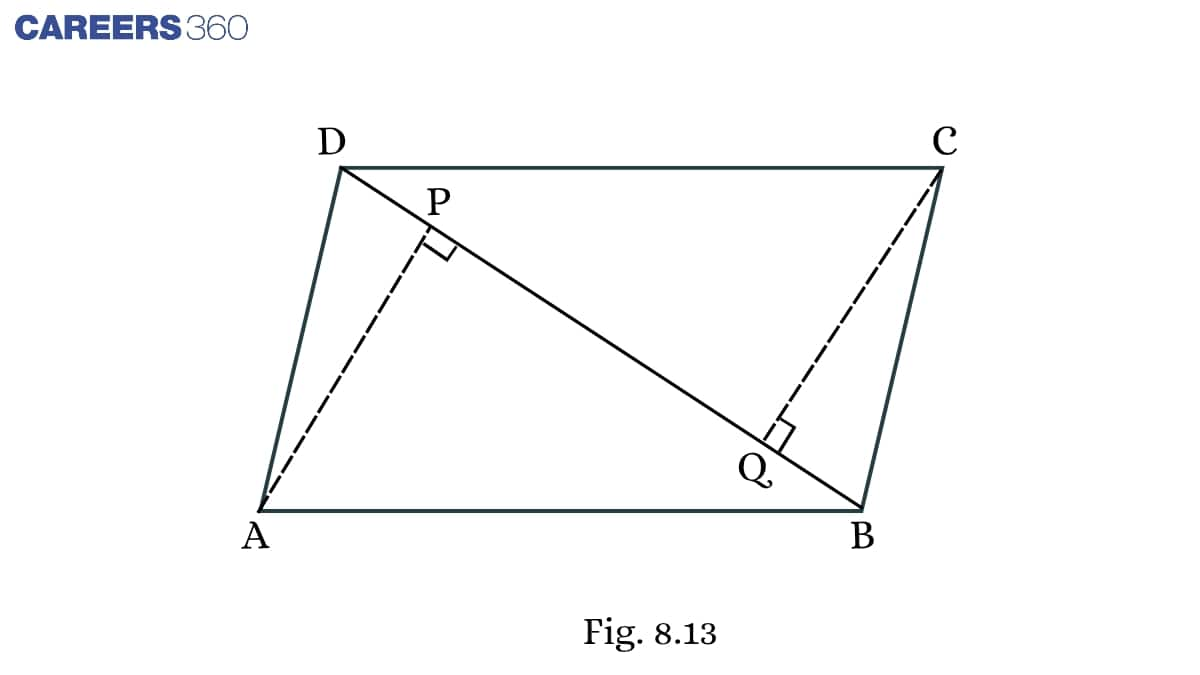
Solution:
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD.
To prove: AP=CQ
Proof: In ΔAPBandΔCQD,
∠ APB= ∠ CQD (Each 90∘)
∠ ABP= ∠ CDQ (Alternate angles)
AB = CD (Opposite sides of a parallelogram )
Thus, ΔAPB≅ΔCQD (By SAS)
AP=CQ (CPCT)

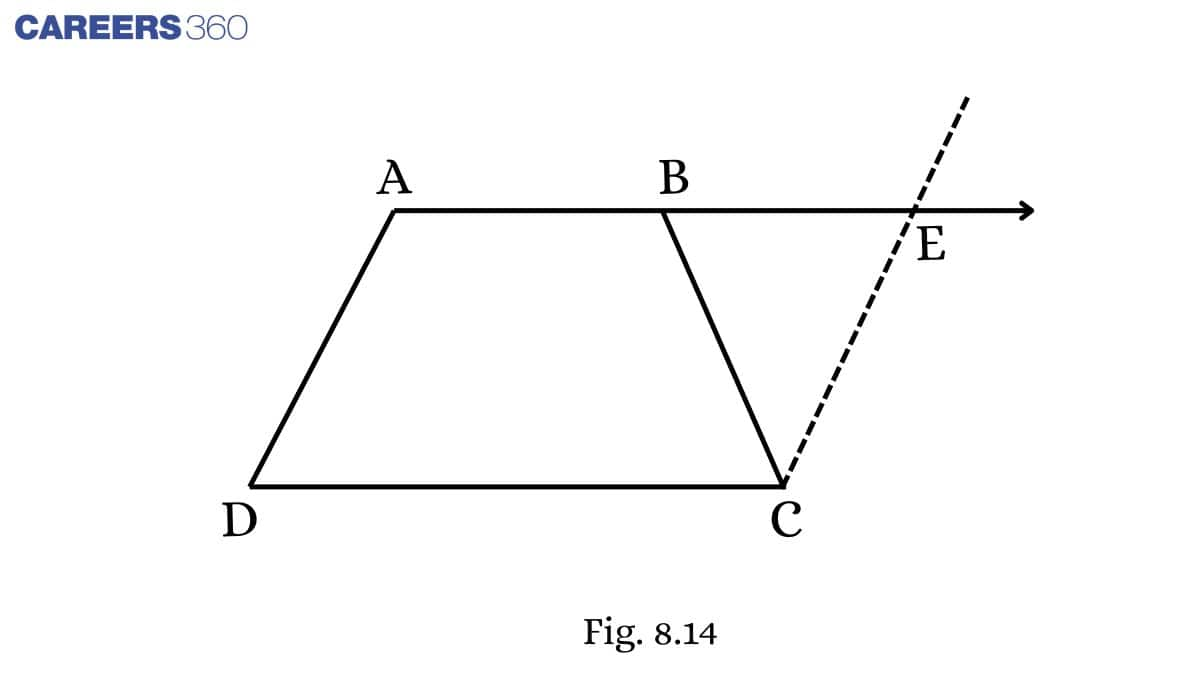
Q7 (i) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.14 ). Show that ∠A=∠B
[ Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

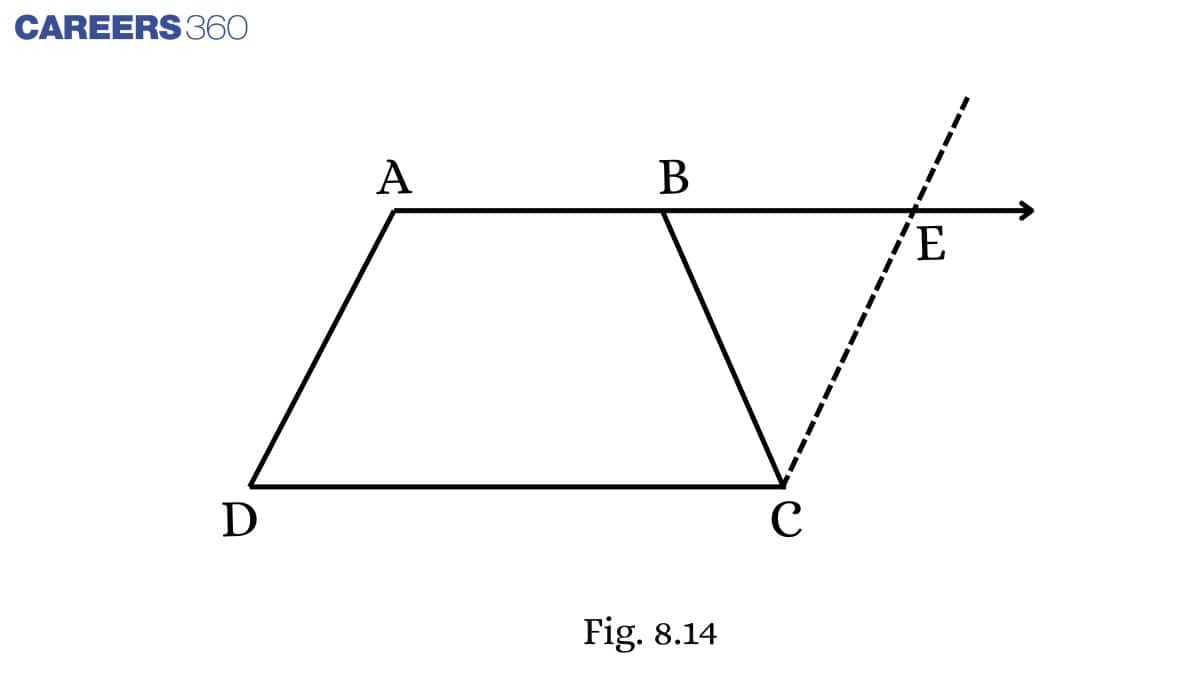
Solution:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: ∠A=∠B
Proof: Let ∠ A be ∠ 1, ∠ ABC be ∠ 2, ∠ EBC be ∠ 3, ∠ BEC be ∠ 4.
In AECD,
AE || DC (Given)
AD || CE (By construction)
Hence, AECD is a parallelogram.
AD = CE.........(1) (Opposite sides of a parallelogram)
AD = BC...........(2) (Given)
From (1) and (2), we get
CE = BC
In △ BCE,
∠3=∠4 ...............(3) (Opposite angles of equal sides)
∠2+∠3=180∘ ..............(4) (Linear pairs)
∠1+∠4=180∘ ...............(5) (Co-interior angles)
From (4) and (5), we get
∠2+∠3=∠1+∠4
∴∠2=∠1→∠B=∠A (Since, ∠3=∠4 )

Q7 (ii) ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that ∠C=∠D [Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

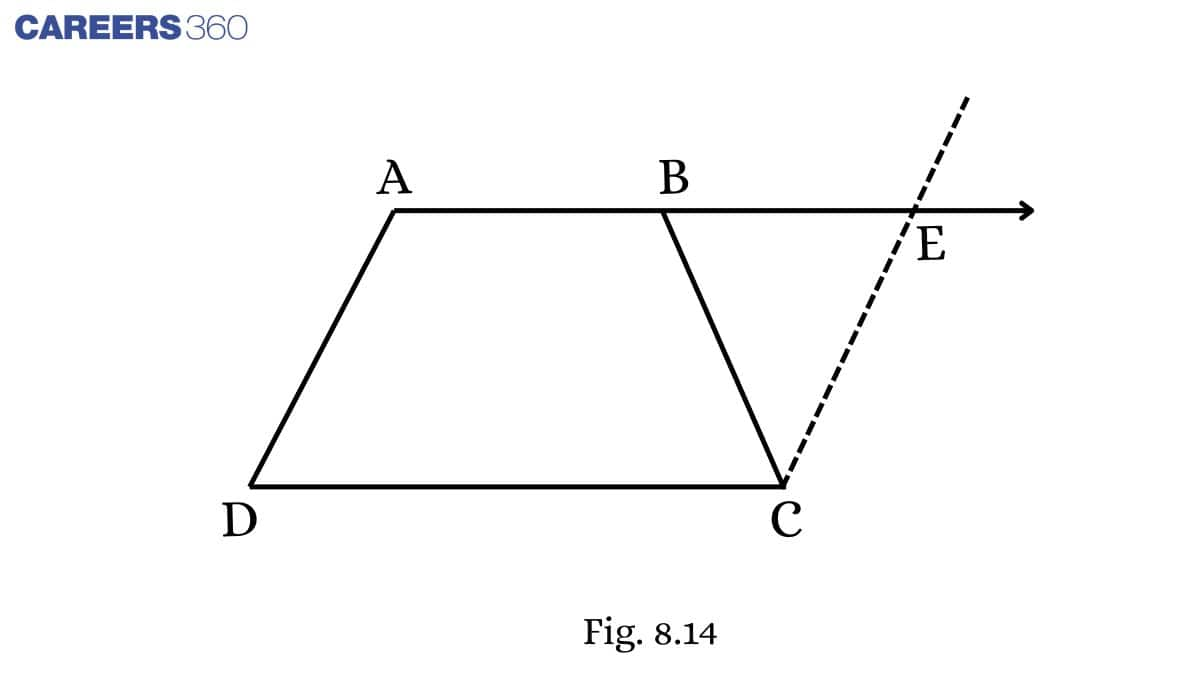
Solution:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: ∠C=∠D
Proof: Let ∠ A be ∠ 1, ∠ ABC be ∠ 2, ∠ EBC be ∠ 3, ∠ BEC be ∠ 4.
∠1+∠D=180∘ (Co-interior angles)
∠2+∠C=180∘ (Co-interior angles)
∴∠1+∠D=∠2+∠C
Thus, ∠C=∠D (Since , ∠1=∠2 )

Q7 (iii) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.13 ). Show that ΔABC≅ΔBAD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

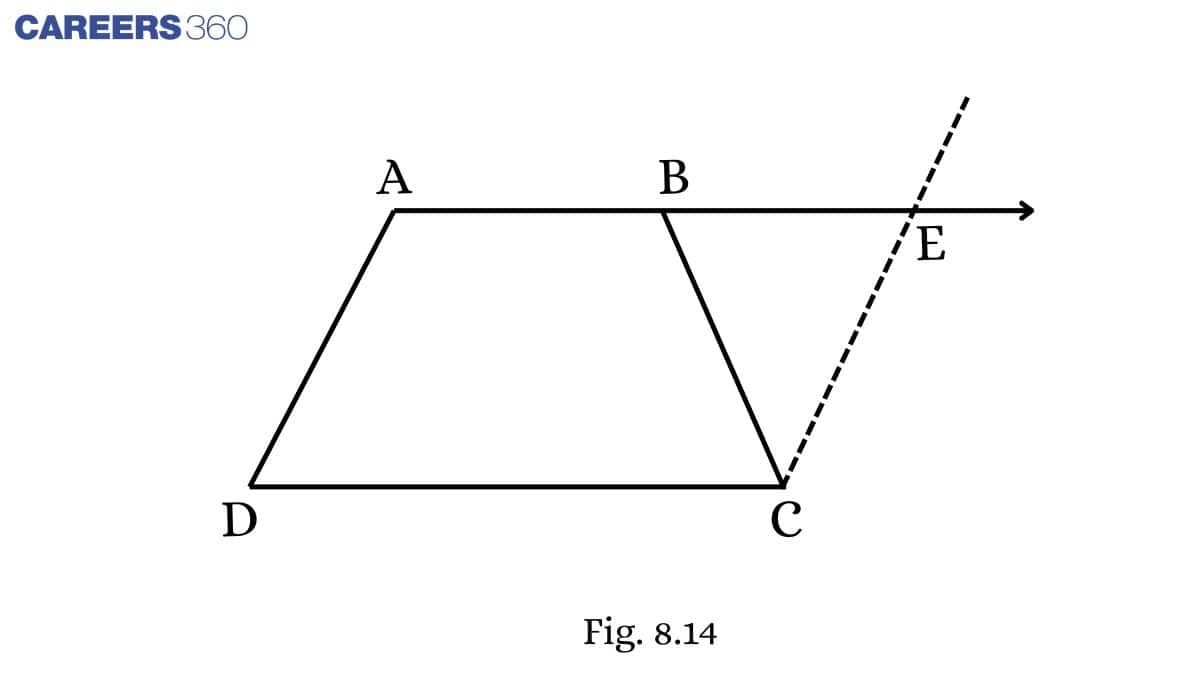
Solution:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: ΔABC≅ΔBAD
Proof: In ΔABCandΔBAD,
BC = AD (Given)
AB = AB (Common)
∠ABC=∠BAD (Proved in (i))
Thus, ΔABC≅ΔBAD (By SAS rule)

Q7 (iv) ABCD is a trapezium in which AB∥CD and AD=BC (see Fig. 8.13 ). Show that diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

Solution:
Given: ABCD is a trapezium in which AB∥CD and AD=BC
To prove: diagonal AC = diagonal BD
Proof: In ΔABCandΔBAD,
BC = AD (Given)
AB = AB (Common)
∠ABC=∠BAD (Proved in (i))
Thus, ΔABC≅ΔBAD (By SAS rule)
diagonal AC = diagonal BD (CPCT)