NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

Edited By Ramraj Saini | Updated on Oct 06, 2023 08:02 AM IST

NCERT Solutions For Class 9 Maths Chapter 1 Number Systems

Number Systems Class 9 Questions And Answers are provided here. These NCERT solutions are prepared by expert team at Careers360 according to latest CBSE syllabus 2023-24. Apart from school exams, the solutions are also beneficial if you are aiming for exams like- National Talent Search Examination (NTSE), Indian National Olympiad (INO), SSC, CAT, etc. The Chapter starts with an introduction which includes rational numbers, whole numbers, and integers followed by important topics like irrational numbers, real numbers, how to represent real numbers on the number line, operations on real numbers, and many more.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions For Class 9 Maths Chapter 1 Number Systems
Number Systems Class 9 Questions And Answers PDF Free Download
Number Systems Class 9 Solutions - Important Formulae
Number Systems Class 9 NCERT Solutions (Intext Questions and Exercise)
Number systems class 9 solutions - Topics
Key Features of NCERT Solutions for Class 9 Maths Chapter 1 Number Systems
NCERT Solutions for Class 9 - Chapter Wise
NCERT Solitions for Class 9 - Subject Wise
NCERT Books And NCERT Syllabus

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

With the understanding of rational numbers, we will also study how to represent square roots of 2, 3, 5, and other non-rational numbers. NCERT solutions for Class 9 Maths chapter 1 Number Systems are written keeping important basics in mind so that a student can get 100% out of it. students can find all the NCERT solutions for class 9 here. practice these to command the concepts.

Number Systems Class 9 Questions And Answers PDF Free Download

Download PDF

Number Systems Class 9 Solutions - Important Formulae

Any unique real number can be represented on a number line.

1696559183963

If r = rational number and s = irrational number

Then (r + s), (r – s), (r × s), and (r ⁄ s) all are irrational.

Rules for positive real numbers:

√ab = √a × √b
√(a/b) = √a/√b
(√a + √b) × (√a – √b) = a−b
(a + √b) × (a − √b) = a² − b
(√a+√b)² = a² + 2√ab + b

To rationalise the denominator of 1/√(a + b), one must multiply it by √(a – b) / √(a – b), where a and b are both integers.

Suppose a = real number (greater than 0) and p and q are rational numbers:

a^p × b^p = (ab)^(p)
(a^p)^q = a^pq
a^p / a^q = (a)^(p-q)
a^p / b^p = (a/b)^p

Free download NCERT Solutions for Class 9 Maths Chapter 1 Number Systems for CBSE Exam.

Number Systems Class 9 NCERT Solutions (Intext Questions and Exercise)

Number systems class 9 questions and answers - Exercise 1.1

Q1 Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0?

Answer:

Any number that can represent in the form of $\frac{p}{q}$ $(where \ q \neq 0)$ is a rational number

Now, we can write 0 in the form of $\frac{p}{q}$ for eg. $\frac{0}{1},\frac{0}{2},\frac{0}{-1}$ etc.

Therefore, 0 is a rational number.

Q2 Find six rational numbers between 3 and 4.

Answer:

There are an infinite number of rational numbers between 3 and 4. one way to take them is
$\Rightarrow 3 = \frac{21}{7} \ and \ 4 = \frac{28}{7}$
Therefore, six rational numbers between 3 and 4 are $\frac{22}{7}, \frac{23}{7},\frac{24}{7},\frac{25}{7},\frac{26}{7},\frac{27}{7}$

Q3 Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ .

Answer:

We can write
$\Rightarrow \frac{3}{5}= \frac{3\times 6}{5\times 6} = \frac{18}{30}$
And
$\Rightarrow \frac{4}{5}= \frac{4\times 6}{5\times 6} = \frac{24}{30}$
Therefore, five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ . are $\frac{19}{30},\frac{20}{30},\frac{21}{30},\frac{22}{30},\frac{23}{30},$

Q4 (i) State whether the following statements are true or false. Give reasons for your answers. (i)Every natural number is a whole number.

Answer:

(i) TRUE
The number that is starting from 1, i.e 1, 2, 3, 4, 5, 6, .................. are natural numbers
The number that is starting from 0. i.e, 0, 1, 2, 3, 4, 5.............are whole numbers
Therefore, we can clearly see that the collection of whole numbers contains all natural numbers.

Q4 (ii) State whether the following statements are true or false. Give reasons for your answers. (ii) Every integer is a whole number.

Answer:

(ii) FALSE
Because integers may be negative or positive but whole numbers are always positive. for eg. -1 is an integer but not a whole number.

Q4 (iii) State whether the following statements are true or false. Give reasons for your answers.(iii) Every rational number is a whole number.

Answer:

(iii) FALSE
Numbers that can be represented in the form of $\frac{p}{q} \ ( where \ q \neq 0)$ are a rational number.
And numbers that are starting from 0 i.e. 0,1,2,3,4,......... are whole numbers
Therefore, we can clearly see that every rational number is not a whole number for eg. $\frac{3}{4}$ is a rational number but not a whole number

Class 9 maths chapter 1 question answer - Exercise 1.2

Q1 (i) State whether the following statements are true or false. Justify your answers. (i) Every irrational number is a real number.

Answer:

(i) TRUE
Since the real numbers are the collection of all rational and irrational numbers.

Q1 (ii) State whether the following statements are true or false. Justify your answers. (ii) Every point on the number line is of the form $\sqrt{m}$ , where m is a natural number.

Answer:

(ii) FALSE
Because negative numbers are also present on the number line and no negative number can be the square root of any natural number

Q1 (iii) State whether the following statements are true or false. Justify your answers. (iii) Every real number is an irrational number.

Answer:

(iii) FALSE
As real numbers include both rational and irrational numbers. Therefore, every real number cannot be an irrational number.

For eg. 4 is a real number but not an irrational number

Q2 Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Answer:

NO, Square root of all positive integers is not irrational. For the eg square of 4 is 2 which is a rational number.

Q3 Show how $\sqrt{5}$ can be represented on the number line.

Answer:

We know that
$\sqrt{5} = \sqrt{(2)^2+(1)^2}$
Now,
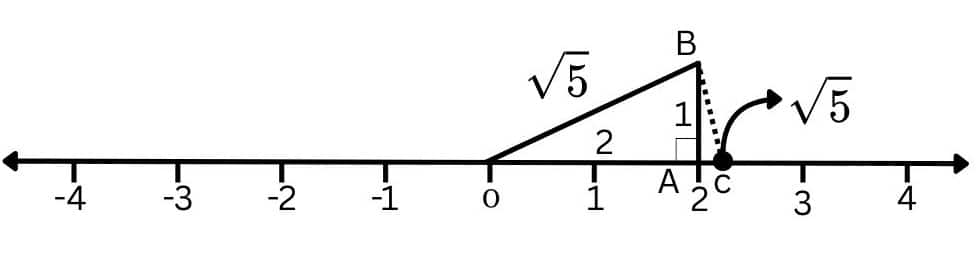
1639723473448 Let OA be a line of length 2 unit on the number line. Now, construct AB of unit length perpendicular to OA. and join OB.
Now, in right angle triangle OAB, by Pythagoras theorem
$OB = \sqrt{(2)^2+(1)^2}=\sqrt{5}$
Now, take O as centre and OB as radius, draw an arc intersecting number line at C. Point C represent $\sqrt{5}$ on a number line.

Class 9 maths chapter 1 question answer - Exercise: 1.3

Q1 (i) Write the following in decimal form and say what kind of decimal expansion each has : (i) $\frac{36}{100}$

Answer:

We can write $\frac{36}{100}$ as
$\Rightarrow \frac{36}{100}= 0.36$
Since the decimal expansion ends after a finite number of steps. Hence, it is terminating

Q1 (ii) Write the following in decimal form and say what kind of decimal expansion each has : (ii) $\frac{1}{11}$

Answer:

We can rewrite $\frac{1}{11}$ as

$\Rightarrow \frac{1}{11}= 0.09090909..... = 0.\overline{09}$
Since decimal expansion repeats itself so it is a non-terminating recurring decimal expansion.

Q1 (iii) Write the following in decimal form and say what kind of decimal expansion each has : (iii) $4\frac{1}{8}$

Answer:

We can rewrite $4\frac{1}{8}$ as

$\Rightarrow 4\frac{1}{8} = \frac{33}{8}= 4.125$
Since the decimal expansion ends after a finite number. Therefore, it is terminating

Q1 (iv) Write the following in decimal form and say what kind of decimal expansion each has : (iv) $\frac{3}{13}$

Answer:

We can rewrite $\frac{3}{13}$ as

$\Rightarrow \frac{3}{13} = 0.230769230769 = 0.\overline{230769}$
Since decimal expansion repeats itself so it is a non-terminating recurring decimal expansion.

Q1 (v) Write the following in decimal form and say what kind of decimal expansion each has: (v) $\frac{2}{11}$

Answer:

We can rewrite $\frac{2}{11}$ as

$\Rightarrow \frac{2}{11} = 0.181818......= 0.\overline{18}$
Since decimal expansion repeats itself so it is a non-terminating recurring decimal expansion.

Q1 (vi) Write the following in decimal form and say what kind of decimal expansion each has : (vi) $\frac{329}{400}$

Answer:

We can rewrite $\frac{329}{400}$ as

$\Rightarrow \frac{329}{400}= 0.8225$
Since decimal expansion ends after finite no. of figures. Hence, it is terminating.

Q2 You know that $\frac{1}{7}=0.\overline{142857}$ Can you predict what the decimal expansions of $\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7}$ are, without actually doing the long division? If so, how?

Answer:

It is given that $\frac{1}{7}=0.\overline{142857}$

Therefore,

$\Rightarrow \frac{2}{7} = 2\times \frac{1}{7} = 2 \times 0.\overline{142857}= 0.\overline{285714}$

Similarly,

$\Rightarrow \frac{3}{7} = 3\times \frac{1}{7} = 3 \times 0.\overline{142857}= 0.\overline{428571}$

$\Rightarrow \frac{4}{7} = 4\times \frac{1}{7} = 4 \times 0.\overline{142857}= 0.\overline{571428}$

$\Rightarrow \frac{5}{7} = 5\times \frac{1}{7} = 5 \times 0.\overline{142857}= 0.\overline{714285}$

$\Rightarrow \frac{6}{7} = 6\times \frac{1}{7} = 6 \times 0.\overline{142857}= 0.\overline{857142}$

Q3 (i) Express the following in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0. (i) $0.\bar{6}$

Answer:

Let $x = 0.\overline6= 0.6666....$ -(i)

Now, multiply by 10 on both sides

$10x= 6.6666...$

$\Rightarrow 10x = 6 + x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \(using \ (i))$

$\Rightarrow 9x = 6$

$\Rightarrow x = \frac{6}{9} = \frac{2}{3}$

Therefore, $\frac{p}{q}$ form of $0.\bar{6}$ is $\frac{2}{3}$

Q3 (ii) Express the following in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0. (ii) $0.4\bar{7}$

Answer:

We can write $0.4\overline7$ as

$\Rightarrow 0.4\overline7 = \frac{4}{10}+ \frac{0.777..}{10}$ -(i)

Now,

Let $x = 0.\overline7= 0.7777....$ -(ii)

Now, multiply by 10 on both sides

$10x= 7.7777...$

$\Rightarrow 10x = 7 + x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \(using \ (ii))$

$\Rightarrow 9x = 7$

$\Rightarrow x = \frac{7}{9}$
Now, put the value of x in equation (i). we will get

$\Rightarrow 0.4\overline7 = \frac{4}{10}+ \frac{7}{10\times 9}= \frac{4}{10}+ \frac{7}{90} = \frac{36+7}{90} = \frac{43}{90}$

Therefore, $\frac{p}{q}$ form of $0.4\overline7$ is $\frac{43}{90}$

Q3 (iii) Express the following in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0. (iii) $0.\overline{001}$

Answer:

Let $x = 0.\overline{001}= 0.001001....$ -(i)

Now, multiply by 1000 on both sides

$1000x= 1.001001...$

$\Rightarrow 1000x = 1 + x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \(using \ (i))$

$\Rightarrow 999x = 1$

$\Rightarrow x = \frac{1}{999}$

Therefore, $\frac{p}{q}$ form of $0.\overline{001}$ is $\frac{1}{999}$

Q4 Express 0.99999 .... in the form $\frac{p}{q}$ . Are you surprised by your answer?

Answer:

Let $x = 0.\overline{9}= 0.9999....$ -(i)

Now, multiply by 10 on both sides

$10x= 9.999....$

$\Rightarrow 10x = 9 + x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \(using \ (i))$

$\Rightarrow 9x = 9$

$\Rightarrow x = \frac{9}{9} = 1$

Therefore, $\frac{p}{q}$ form of $0.999....$ is 1

The difference between 1 and 0.999999 is o.000001 which is almost negligible.

Therefore, 0.999 is too much closer to 1. Hence, we can write 0.999999.... as 1

Q5 What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.

Answer:

We can rewrite $\frac{1}{17}$ as

$\Rightarrow \frac{1}{17} = 0.05882352941176470588235294117647= 0.\overline{0588235294117647}$
Therefore, there are total 16 number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$

Q6 Look at several examples of rational numbers in the form $\frac{p}{q}$ (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Answer:

We can observe that when q is 2, 4, 5, 8, 10… then the decimal expansion is terminating. For example:

$\frac{3}{2}= 1.5$ , denominator $q = 2^1$

$\frac{8}{5}= 1.6$ , denominator $q = 5^1$

$\frac{15}{10} = 1.5$ , denominator $q =10=2\times 5= 2^1 , 5^1$

Therefore,

It can be observed that the terminating decimal can be obtained in a condition where prime factorization of the denominator of the given fractions has the power of 2 only or 5 only or both.

Q7 Write three numbers whose decimal expansions are non-terminating non-recurring.

Answer:

Three numbers whose decimal expansions are non-terminating non-recurring are
1) 0.02002000200002......
2) 0.15115111511115.......
3) 0.27227222722227.......

Q8 Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ .

Answer:

We can write $\frac{5}{7}$ as

$\Rightarrow \frac{5}{7} = 0.714285714285.... = 0.\overline{714285}$

And $\frac{9}{11}$ as

$\Rightarrow \frac{9}{11} = 0.818181.... = 0.\overline{81}$
Therefore, three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ are

1) 0.72737475....
2) 0.750760770780...
3) 0.790780770760....

Q9 (i) Classify the following numbers as rational or irrational : $\sqrt{23}$

Answer:

We can rewrite $\sqrt{23}$ in decimal form as

$\Rightarrow \sqrt{23} = 4.7958152....$

Now, as the decimal expansion of this number is non-terminating non-recurring.

Therefore, it is an irrational number.

Q9 (ii) Classify the following numbers as rational or irrational : $\sqrt{225}$

Answer:

We can rewrite $\sqrt{225}$ as

$\Rightarrow \sqrt{225} = 15$
We can clearly see that it is a rational number because we can represent it in $\frac{p}{q}$ form

Q9 (iii) Classify the following numbers as rational or irrational : 0.3796

Answer:

We can rewrite 0.3796 as

$\Rightarrow 0.3796 = \frac{3796}{10000}$
Now, we can clearly see that it is a rational number as the decimal expansion of this number is terminating and we can also write it in $\frac{p}{q}$ form.

Q9 (iv) Classify the following numbers as rational or irrational : 7.478478....

Answer:

We can rewrite 7.478478.... as

$\Rightarrow 7.478478.... = 7.\overline{478}$
Now, as the decimal expansion of this number is non-terminating recurring. Therefore, it is a rational number.

Q9 (v) Classify the following numbers as rational or irrational : 1.101001000100001...

Answer:

In the case of number 1.101001000100001...
As the decimal expansion of this number is non-terminating non-repeating. Therefore, it is an irrational number.

Class 9 maths chapter 1 NCERT solutions - Exercise: 1.4

Q1 Visualise 3.765 on the number line, using successive magnification.

Answer:

3.765 can be visualised as in the following steps.
First, we draw a number line and mark points on it after that we will divide the number line between points 3 and 4. And then we will divide the points between 3.7 and 3.8 as the number is between both of them.
1639723522139

Q2 Visualise $4.\overline{26}$ on the number line, up to 4 decimal places.

Answer:

We can rewrite $4.\overline{26}$ as $\Rightarrow 4.\overline{26}= 4.262626...$
Now, 4.2626 can be visualised as in the following steps.

1639723563861

Class 9 maths chapter 1 NCERT solutions - Exercise: 1.5

Q1 (i) Classify the following numbers as rational or irrational: $2-\sqrt{5}$

Answer:

Value of $\sqrt{5}$ is 2.23606798....
Now,
$\Rightarrow 2 - \sqrt{5} = 2 - 2.23606798... = -0.23606798...$
Now,
Since the number is in non-terminating non-recurring. Therefore, it is an irrational number.

Q1 (ii) Classify the following numbers as rational or irrational: $\left ( 3+\sqrt{23} \right )-\sqrt{23}$

Answer:

Given number is $\left ( 3+\sqrt{23} \right )-\sqrt{23}$

$\Rightarrow \left ( 3+\sqrt{23} \right )-\sqrt{23} = 3+\sqrt{23}-\sqrt{23} = 3$
Now, it is clearly a rational number because we can represent it in the form of $\frac{p}{q}$

Q1 (iii) Classify the following numbers as rational or irrational: $\frac{2\sqrt{7}}{7\sqrt{7}}$

Answer:

Given number is $\frac{2\sqrt{7}}{7\sqrt{7}}$

$\Rightarrow \frac{2\sqrt{7}}{7\sqrt{7}} = \frac{2}{7}$
As we can clearly see that it can be represented in $\frac{p}{q}$ form. Therefore, it is a rational number.

Q1 (iv) Classify the following numbers as rational or irrational: $\frac{1}{\sqrt{2}}$

Answer:

Given number is $\frac{1}{\sqrt{2}}$

$\Rightarrow \frac{1}{\sqrt{2}}= \frac{\sqrt{2}}{2}=\frac{1.41421356..}{2} =0.7071068...$
Now,
Clearly, as the decimal expansion of this expression is non-terminating and non-recurring. Therefore, it is an irrational number.

Q1 (v) Classify the following numbers as rational or irrational: $2\pi$

Answer:

Given number is $2\pi$
We know that the value of $\pi = 3.14159265...$
Now,
$\Rightarrow 2\pi = 2\times 3.14159265... = 6.2831853...$
Now,
Clearly, as the decimal expansion of this expression is non-terminating and non-recurring. Therefore, it is an irrational number.

Q2 (i) Simplify each of the following expressions: $(3+\sqrt{3})(2+\sqrt{2})$

Answer:

Given number is $(3+\sqrt{3})(2+\sqrt{2})$
Now, we will reduce it into
$\Rightarrow (3+\sqrt{3})(2+\sqrt{2})= 3.2+3.\sqrt{2}+\sqrt{3}.2+\sqrt{3}.\sqrt{2}$
$= 6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$

Therefore, answer is $6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$

Q2 (ii) Simplify each of the following expressions: $\left (3+\sqrt{3} \right )\left ( 3-\sqrt{3} \right )$

Answer:

Given number is

$\left (3+\sqrt{3} \right )\left ( 3-\sqrt{3} \right )$
Now, we will reduce it into
$\Rightarrow (3+\sqrt{3})(3-\sqrt{3})= \left ( (3)^2-(\sqrt{3})^2 \right )$ $\left ( using \ (a+b)(a-b)=a^2-b^2 \right )$
$=9 - 3 = 6$

Therefore, answer is 6

Q2 (iii) Simplify each of the following expressions: $\left (\sqrt{5}+\sqrt{2} \right )^{2}$

Answer:

Given number is $\left (\sqrt{5}+\sqrt{2} \right )^{2}$

Now, we will reduce it into
$\Rightarrow \left (\sqrt{5}+\sqrt{2} \right )^{2} = \left ( (\sqrt{5})^2+(\sqrt{2})^2+2.\sqrt{5}.\sqrt{2} \right )$ $\left ( using \ (a+b)^2=a^2+b^2 +2ab\right )$
$=5+2+2\sqrt{10}$
$=7+2\sqrt{10}$

Therefore, the answer is $7+2\sqrt{10}$

Q2 (iv) Simplify each of the following expressions: $\left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )$

Answer:

Given number is $\left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )$

Now, we will reduce it into
$\Rightarrow \left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )= \left ( (\sqrt{5})^2-(\sqrt{2})^2 \right )$ $\left ( using \ (a+b)(a-b)=a^2-b^2\right )$
$=5-2$
$=3$

Therefore, the answer is 3 .

Q3 Recall, $\pi$ is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, $\pi=\frac{c}{d}$ ⋅ This seems to contradict the fact that $\pi$ is irrational. How will you resolve this contradiction?

Answer:

There is no contradiction.
When we measure a length with scale or any other instrument, we only obtain an approximate rational value. We never obtain an exact value.
For this reason, we cannot say that either c or d is irrational.
Therefore, the fraction $\frac{c}{d}$ is irrational. Hence, the value of $\pi$ is approximately equal to $\frac{22}{7} = 3.142857....$

Therefore, $\pi$ is irrational.

Q4 Represent $\sqrt{9.3}$ on the number line.

Answer:

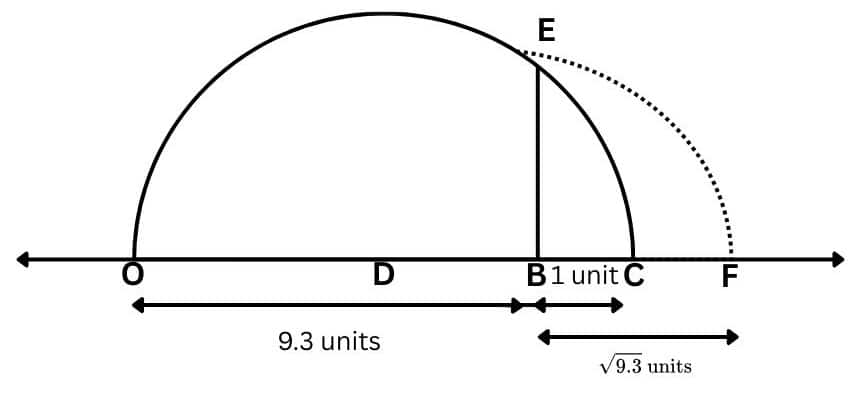
1639723609742 Draw a line segment OB of 9.3 unit. Then, extend it to C so that BC = 1 unit. Find the mid-point D of OC and draw a semi-circle on OC while taking D as its centre and OD as the radius. Now, Draw a perpendicular to line OC passing through point B and intersecting the semi-circle at E. Now, Take B as the centre and BE as radius, draw an arc intersecting the number line at F. the length BF is $9\sqrt{3}$ units.

Q5 (i) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}}$

Answer:

Given number is $\frac{1}{\sqrt{7}}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7} = \frac{1}{\sqrt 7}\times \frac{\sqrt 7}{\sqrt 7 } = \frac{\sqrt7}{7}$

Therefore, the answer is $\frac{\sqrt7}{7}$

Q5 (ii) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}-\sqrt{6}}$

Answer:

Given number is $\frac{1}{\sqrt{7}-\sqrt{6}}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7-\sqrt6} = \frac{1}{\sqrt 7-\sqrt 6}\times \frac{\sqrt 7+\sqrt 6 }{\sqrt 7+\sqrt 6 } = \frac{\sqrt7+\sqrt 6}{(\sqrt7)^2-(\sqrt6)^2} = \frac{\sqrt7+\sqrt6}{7-6}$ $= \sqrt7+\sqrt6$

Therefore, the answer is $\sqrt7+\sqrt6$

Q5 (iii) Rationalise the denominators of the following: $\frac{1}{\sqrt{5}+\sqrt{2}}$

Answer:

Given number is $\frac{1}{\sqrt{5}+\sqrt{2}}$

Now, on rationalisation, we will get

$\\= \frac{1}{\sqrt 5+\sqrt2} \\\\= \frac{1}{\sqrt 5+\sqrt 2}\times \frac{\sqrt 5-\sqrt 2 }{\sqrt 5-\sqrt 2 }\\\\ = \frac{\sqrt5-\sqrt 2}{(\sqrt5)^2-(\sqrt2)^2} \\\\= \frac{\sqrt5-\sqrt2}{5-2}$
$= \frac{\sqrt5-\sqrt2}{3}$

Therefore, the answer is $\frac{\sqrt5-\sqrt2}{3}$

Q5 (iv) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}-2}$

Answer:

Given number is $\frac{1}{\sqrt{7}-2}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7-2} = \frac{1}{\sqrt 7- 2}\times \frac{\sqrt 7+ 2 }{\sqrt 7+ 2 } = \frac{\sqrt7+ 2}{(\sqrt7)^2-(2)^2} = \frac{\sqrt7+2}{7-4}$
$= \frac{\sqrt7+2}{3}$

Therefore, answer is $\frac{\sqrt7+2}{3}$

Class 9 number systems ncert solutions - Exercise: 1.6

Q1 (i) Find : $64^{\frac{1}{2}}$

Answer:

Given number is $64^{\frac{1}{2}}$

Now, on simplifying it we will get

$\Rightarrow 64^{\frac{1}{2}} = (8^2)^\frac{1}{2} = 8$

Therefore, answer is 8

Q1 (ii) Find : $32^{\frac{1}{5}}$

Answer:

Given number is $32^{\frac{1}{5}}$

Now, on simplifying it we will get

$\Rightarrow 32^{\frac{1}{5}} = (2^5)^\frac{1}{5} = 2$

Therefore, the answer is 2

Q1 (iii) Find : $125^{\frac{1}{3}}$

Answer:

Given number is $125^{\frac{1}{3}}$

Now, on simplifying it we will get

$\Rightarrow 125^{\frac{1}{3}} = (5^3)^\frac{1}{3} = 5$

Therefore, the answer is 5

Q2 (i) Find : $9^{\frac{3}{2}}$

Answer:

Given number is $9^{\frac{3}{2}}$

Now, on simplifying it we will get

$\Rightarrow 9^{\frac{3}{2}} = (3^2)^\frac{3}{2} = 3^3 = 27$

Therefore, the answer is 27

Q2 (ii) Find : $32^{\frac{2}{5}}$

Answer:

Given number is $32^{\frac{2}{5}}$

Now, on simplifying it we will get

$\Rightarrow 32^{\frac{2}{5}} = (2^5)^\frac{2}{5} = 2^2 = 4$

Therefore, the answer is 4

Q2 (iii) Find : $16^{\frac{3}{4}}$

Answer:

Given number is $16^{\frac{3}{4}}$

Now, on simplifying it we will get

$\Rightarrow 16^{\frac{3}{4}} = (2^4)^\frac{3}{4} = 2^3 = 8$

Therefore, the answer is 8

Q2 (iv) Find : $125^{\frac{-1}{3}}$

Answer:

Given number is $125^{\frac{-1}{3}}$

Now, on simplifying it we will get

$\Rightarrow 125^{\frac{-1}{3}} = (5^3)^\frac{-1}{3} = 5^{-1} = \frac{1}{5}$
Therefore, the answer is $\frac{1}{5}$

Q3 (i) Simplify : $2^{\frac{2}{3}}.2^{\frac{1}{5}}$

Answer:

Given number is $2^{\frac{2}{3}}.2^{\frac{1}{5}}$

Now, on simplifying it we will get

$\Rightarrow 2^{\frac{2}{3}}.2^{\frac{1}{5}} = 2^{\frac{2}{3}+\frac{1}{5}} = 2^{\frac{10+3}{15}} = 2^\frac{13}{15}$ $\left ( \because a^n.a^m = a^{n+m} \right )$

Therefore, the answer is $2^{\frac{13}{15}}$

Q3 (ii) Simplify : $\left (\frac{1}{3^{3}} \right )^{7}$

Answer:

Given number is $\left (\frac{1}{3^{3}} \right )^{7}$

Now, on simplifying it we will get

$\Rightarrow \left ( \frac{1}{3^3} \right )^7= \frac{1^7}{3^{3\times7}} = \frac{1}{3^{21}} = 3^{-21}$ $\left ( \because (a^n)^m = a^{n.m} \ and \ \frac{1}{a^m}= a^{-m}\right )$

Therefore, the answer is $3^{-21}$

Q3 (iii) Simplify : $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}$

Answer:

Given number is $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}$

Now, on simplifying it we will get

$\Rightarrow \frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}} = 11^{\frac{1}{2}-\frac{1}{4}}= 11^{\frac{2-1}{4}} = 11^\frac{1}{4}$ $\left ( \because \frac{a^n}{a^m}= a^{n-m}\right )$
Therefore, the answer is $11^{\frac{1}{4}}$

Q3 (iv) Simplify : $7^{\frac{1}{2}}.8^{\frac{1}{2}}$

Answer:

Given number is $7^{\frac{1}{2}}.8^{\frac{1}{2}}$

Now, on simplifying it we will get

$\Rightarrow 7^{\frac{1}{2}}.8^{\frac{1}{2}}= (7\times8)^{\frac{1}{2}} = 56^{\frac{1}{2}}$ $\left ( \because a^n.b^n=(a.b)^n\right )$
Therefore, the answer is $56^{\frac{1}{2}}$

Number systems class 9 solutions - Topics

Irrational Numbers
Real Numbers and their Decimal Expansions
Representing Real Numbers on the Number Line
Operations on Real Numbers
Laws of Exponents for Real Numbers

Also Read :

Key Features of NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

In-depth Knowledge: This chapter provides in-depth knowledge of numbers and their applications.
Conceptual Clarity: By studying this chapter, you will gain a profound conceptual understanding of the number system.
Assistance: NCERT solutions for Class 9 Maths Chapter 1 are available to assist you when you encounter difficulties with problems related to this chapter.
Total Exercises: The chapter consists of a total of 6 exercises.
Number of Questions: These exercises encompass 27 questions in total.
Weightage: Chapter 1 holds a weightage of 8 marks in the CBSE Class 9 final examination.
Comprehensive Solutions: NCERT maths chapter 1 class 9 cover the solutions to each and every question present in the practice exercises of the NCERT syllabus.

Interested students can practice class 9 maths ch 1 question answer using the following exercises.

NCERT Solutions for Class 9 - Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Number Systems
Chapter 2	Polynomials
Chapter 3	Coordinate Geometry
Chapter 4	Linear Equations In Two Variables
Chapter 5	Introduction to Euclid's Geometry
Chapter 6	Lines And Angles
Chapter 7	Triangles
Chapter 8	Quadrilaterals
Chapter 9	Areas of Parallelograms and Triangles
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Heron’s Formula
Chapter 13	Surface Area and Volumes
Chapter 14	Statistics
Chapter 15	Probability

NCERT Solitions for Class 9 - Subject Wise

NCERT Solutions for Class 9 Maths

NCERT Solutions for Class 9 Science

How to Use NCERT Solutions for Class 9 Maths Chapter 1 Number Systems?

First of all, go through the conceptual text given in the book before the exercises.
After covering the conceptual theory, you must go through some examples to understand the application of that particular concept.
After observing the application, come to the practice exercises available in the textbook
While solving the practice exercises, you can take the help of NCERT solutions for Class 9 Maths chapter 1 Number Systems to boost your preparation.

NCERT Books And NCERT Syllabus

Keep working hard & happy learning!

Frequently Asked Questions (FAQs)

1. What are the important topics in NCERT class 9 maths chapter 1 Number Systems ?

The basic concept of the number system, rational numbers, whole numbers, and integers, irrational numbers, real numbers, representation of real numbers on the number line, operations on real numbers are the important topics of this chapter. Students can practice math 9th class chapter 1 solutions to get in-depth understanding of concepts.

2. Which are the most difficult chapters of NCERT Class 9 Maths syllabus?

Most of the students consider geometry especially triangles as the most difficult chapter in the CBSE Class 9 Maths. To solve more problems students can also refer to NCERT exemplar questions.

3. Does CBSE provides the solutions of NCERT for Class 9 Maths ?

No, CBSE doesn’t provide NCERT solutions for any class or subject. To get a good score in CBSE exams students can follow NCERT syllabus and book.

4. Where can I find the complete solutions of NCERT for Class 9 Maths ?

Here, students can get detailed NCERT solutions for Class 9 Maths by clicking on the link. practicing these real numbers class 9 solutions are important as these provide confidence to students which ultimately lead to high score.

5. How does the NCERT solutions are helpful ?

NCERT solutions are helpful for the students if they stuck while solving NCERT problems. Also, these solutions are provided in a very detailed manner which will give them conceptual clarity.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

IGNOU BEd Answer Key 2025: Download OMR Sheet Here

Dec 13, 2024

TOSS Admission 2024-25: Apply for SSC & Inter TS Open School Admission @telanganaopenschool.org

Dec 13, 2024

IGNOU Registration 2025 (Statred), January Session, Last Date, Fess, Link, Apply Online

Dec 12, 2024

10 Ways To Think Straight, Without Bias

Dec 12, 2024

5 Apps To Help You Avoid Distractions, Become More Productive

Dec 12, 2024

Class 9 NSTSE 5-Year Analysis: Know Which Topics Get More Weightage And Why

Dec 12, 2024

How to Make APAAR ID via School, DigiLocker : Step-by-Step Guide

Dec 11, 2024

DBSE Admit Card 2025 for Class 10th and 12th

Dec 11, 2024

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Admit Card

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Result

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

NCERT Solutions For Class 9 Maths Chapter 1 Number Systems

Number Systems Class 9 Questions And Answers PDF Free Download

Number Systems Class 9 Solutions - Important Formulae

Number Systems Class 9 NCERT Solutions (Intext Questions and Exercise)

Number systems class 9 solutions - Topics

Key Features of NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

NCERT Solutions for Class 9 - Chapter Wise

NCERT Solitions for Class 9 - Subject Wise

NCERT Books And NCERT Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

National Means Cum-Merit Scholarship

Himachal Pradesh Board of Secondary Education 10th Examination

West Bengal Board 12th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app