Careers360 Logo
Management and Business Administration
Search Colleges, Exams, Schools & more

Popular Searches

    NCERT Exemplar Class 9 Maths Solutions Chapter 1 Number Systems

    Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with

    Plan, Prepare & Make the Best Career Choices

    NCERT Exemplar Class 9 Maths Solutions Chapter 1 Number Systems

    Edited By Ravindra Pindel | Updated on Aug 31, 2022 11:38 AM IST

    NCERT Exemplar Class 9 Maths solutions chapter 1 provide detailed answers for questions related to Number System. These problems and their solutions are devised for a better knowledge of the chapter 1 of NCERT Class 9 Maths Book. These solutions are extremely useful in understanding the concepts and know-how of real numbers. Experts have created these NCERT exemplar solutions for Class 9 Maths chapter 1 with a thorough analysis.

    This Story also Contains
    1. NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.1
    2. NCERT Exemplar Maths Solutions Class 9 Chapter 1: Exercise-1.2
    3. Question:1
    4. NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.3
    5. NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.4
    6. Question:1
    7. NCERT Exemplar Solutions Class 9 Maths Chapter 1 Number System Important Topics:
    8. NCERT Class 9 Maths Exemplar Solutions for Other Chapters:
    9. Features of NCERT Exemplar Class 9 Maths Solutions Chapter 1 Number System:

    The NCERT exemplar Class 9 Maths chapter 1 solutions provided for exemplar problems are detailed and expressive. These are helpful to pinpoint the critical understanding of concepts. The NCERT exemplar Class 9 Maths solutions chapter 1 are in accord with the CBSE syllabus for Class 9.

    Also, read - NCERT Solutions for Class 9 Maths

    NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.1

    Question:1

    Every rational number is:
    (A)A natural number
    (B)An integer
    (C)A real number
    (D) A whole number

    Answer:

    Answer: [C]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Examples: 4/5, 2/3, -6/7
    (A) All the positive integers from 1 to infinity are natural numbers. These cannot be fractions.
    Examples: 1, 2, 3, 4 and so on
    (B) An integer is a number which can be written without fractional components or decimal representation. They can be positive, negative or zero.
    Examples: \left \{ .......,-4,-3,-2,-1,0,1,2,3,4,......... \right \}
    (C) All numbers that we generally use are real numbers. They can be positive, negative, decimal, whole, natural, integer etc.
    Examples: 0.123, -2.5,0,2,5,6.3456
    (D) All the positive integers from 0 to infinity are whole numbers. These cannot be fractions.
    Examples: 0, 1, 2, 3, 4 and so on
    From the above definitions we can easily see that every rational number is a real number. Therefore option (C) is correct.

    Question:2

    Between two rational numbers:

    (A)There is no rational number
    (B)there is exactly one rational number
    (C)there are infinitely many rational numbers
    (D)no irrational number

    Answer:

    Answer: [C]
    Solution.
    Firstly let us define a rational number.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Examples: 4/5, 2/3, -6/7
    So we can say that it is a type of real number.
    Similarly we can see that irrational numbers are real numbers which cannot be represented as simple fractions.
    Examples: \sqrt{2},\sqrt{3},\pi
    So we can say that between two rational numbers, there are infinitely many rational numbers.
    For Example: between rational numbers 5 and 4, there are rational numbers like 4.1, 4.11, 4.12, 4.13………and so on.
    Therefore option (C) is correct.

    Question:3

    Decimal representation of a rational number cannot be :
    (A)Terminating
    (B)non-terminating
    (C)non-terminating repeating
    (D)non-terminating non-repeating

    Answer:

    Answer: [D]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Examples: 4/5, 2/3, -6/7
    Terminating decimals have a finite number of digits after decimal point,
    Examples: 1/2 = 0.5, 3/5 = 0.6
    Non terminating decimals are the ones which keep on continuing after decimal point.
    Examples: 1/3 = 0.3333..., 5/11 = 0.454545....
    Recurring decimals are those non terminating decimals which have a particular pattern/sequence that keeps on repeating itself after the decimal point. They are also called repeating decimals.
    Examples: 1/3 = 0.33333....., 4/11 = 0.363636....
    Non-Recurring decimals are those non terminating decimals which do not have a particular pattern/sequence after the decimal point. They are also called non repeating decimals.
    Examples:
    \sqrt{2}=1.414213562373
    \sqrt{3}=1.732050807568
    \pi =3.14159265359
    So by the above definitions we can see that the decimal representation of a rational number cannot be non-terminating non repeating because decimal expansion of rational number is either terminating or non-terminating recurring (repeating).
    Therefore option (D) is correct.

    Question:4

    The product of any two irrational number is
    (A)always an irrational number
    (B)always a rational number
    (C)always an integer
    (D)sometimes rational, sometimes irrational

    Answer:

    Answer: [D]
    Solution.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Examples: \sqrt{2},\sqrt{3},\pi
    The product of two irrational numbers can be rational or irrational depending on the two numbers.
    For example, \sqrt{2}\times \sqrt{2} is 2 which is a rational number
    whereas \sqrt{2}\times \sqrt{3} is \sqrt{6} which is an irrational number.
    Therefore option (D) is correct.

    Question:5

    The decimal expansion of the number \sqrt{2} is.
    (A) A finite decimal
    (B) 1.41421
    (C) non-terminating recurring
    (D) non-terminating non-recurring

    Answer:

    Answer: [D]
    Solution.
    Terminating decimals have a finite number of digits after decimal point,
    Examples: 1/2 = 0.5, 3/5 = 0.6
    Non terminating decimals are the ones which keep on continuing after decimal point.
    Examples: 1/3 = 0.33333...., 5/11 = 0.454545...
    Recurring decimals are those non terminating decimals which have a particular pattern/sequence that keeps on repeating itself after the decimal point. They are also called repeating decimals.
    Examples: 1/3 = 0.33333..., 4/11 = 0.363636....
    Non-Recurring decimals are those non terminating decimals which do not have a particular pattern/sequence after the decimal point. They are also called non repeating decimals.
    Examples:
    \sqrt{2}=1.414213562373
    \sqrt{3}=1.732050807568
    \pi =3.14159265359
    So, the decimal expansion of the number \sqrt{2} is non-terminating non-recurring. It is an irrational number which is a non-terminating non-recurring decimal expansion.
    Therefore option (D) is correct.

    Question:6

    Which of the following is irrational?
    (A) \sqrt{\frac{4}{9}}
    (B) \frac{\sqrt{12}}{\sqrt{3}}
    (C) \sqrt{7 }
    (D) \sqrt{81}

    Answer:

    Answer: [C]
    Solution.

    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Examples: \sqrt{2},\sqrt{3},\pi
    \sqrt{\frac{4}{9}}=\frac{2}{3} (rational)
    \frac{\sqrt{12}}{\sqrt{3}}=\frac{2\sqrt{3}}{\sqrt{3}}=2 (rational)
    \sqrt{81}=9 (rational)
    but \sqrt{7} is an irrational number.
    Therefore option (C) is correct.

    Question:7

    Which of the following is irrational?
    (A) 0.14
    (B) 0.14\overline{16}
    (C) 0.\overline{1416}
    (D) 0.4014001400014

    Answer:

    Answer: [D]
    Solution.

    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Examples: \sqrt{2},\sqrt{3},\pi
    Irrational cannot be expressed in form of p/q form and its decimal expansion is non- terminating non-recurring decimal expansions.
    Non-Recurring non terminating decimals do not have a particular pattern/sequence after the decimal point. They are also called non repeating decimals.
    Examples:
    \sqrt{2}=1.414213562373
    \sqrt{3}=1.732050807568
    \pi =3.14159265359
    In the given options, only option D is non-terminating non-recurring decimal as it satisfies the above definition.
    Therefore option (D) is correct.

    Question:8

    A rational number between \sqrt{2} and \sqrt{3} is –
    (A) \frac{\sqrt{2}+\sqrt{3}}{2}
    (B) \frac{\sqrt{2}.\sqrt{3}}{2}
    (C) 1.5
    (D) 1.8

    Answer:

    Answer: [C]
    Solution.

    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Now, we have \sqrt{2}=1.414 and \sqrt{3}= 1.732
    (A) \frac{\sqrt{2}+\sqrt{3}}{2} cannot be represented as simple fraction hence it is irrational.
    (B) \frac{\sqrt{2}.\sqrt{3}}{2} =\frac{\sqrt{3}}{\sqrt{2}}=\sqrt{\frac{3}{2}}=\sqrt{1.5} cannot be represented as simple fraction hence it is irrational.
    (C) 1.5 is a rational number between \sqrt{2}=1.414 and \sqrt{3}= 1.732
    Q 1.414 < 1.5 < 1.732
    (D) 1.8 is a rational number but does not lie between     \sqrt{2}=1.414 and \sqrt{3}= 1.732.
    Q 1.732 < 1.8

    Therefore option (C) is correct.

    Question:9

    The value of 1.999 ___in the form \frac{p}{q} where p and q are integers and q \neq0, is
    (A)\frac{19}{10}
    (B)\frac{1999}{1000}
    (C)2
    (D)\frac{1}{9}

    Answer:

    Answer. [C]
    Solution.
    Let x = 1.999……
    Since, one digit is repeating, we multiply x by 10
    we get, 10x = 19.999……..
    so, 10x = 18 + 1.999………
    10x = 18 + x
    Therefore, 10x – x = 18, i.e., 9x = 18
    i.e., x= \frac{18}{9}= \frac{2}{1}= 2
    Hence option C is correct answer.

    Question:10

    2\sqrt{3}+\sqrt{3} is equal to –
    (A).2\sqrt{6}
    (B) 6
    (C)3\sqrt{3}
    (D) 4\sqrt{6}

    Answer:

    Answer. [C]
    Solution.
    We can see that both the numbers \sqrt{3} and 2\sqrt{3} are irrational numbers.
    So their decimal representation will be non terminating, non repeating. So we
    cannot find the exact answer by adding their decimal representations.
    Now 2\sqrt{3}+\sqrt{3} can be written as
    = \sqrt{3}\left ( 2+1 \right ) Taking \sqrt{3} common
    Hence the correct answer is 3\sqrt{3}

    Question:11

    \sqrt{10}\times \sqrt{15}is equal to :
    (A)6\sqrt{5}
    (B)5\sqrt{6}
    (C)\sqrt{25}
    (D)10\sqrt{5}

    Answer:

    Answer. [B] 5\sqrt{6}
    Solution.
    We know that
    10= 5\times 2
    15= 5\times 3
    So we have,
    \sqrt{10}\times \sqrt{15}= \sqrt{5\times 2}\times \sqrt{5\times 3}
    This can be written as
    = \sqrt{5\times 5\times2\times3}
    =5 \sqrt{2\times 3}
    =5 \sqrt{6}
    Therefore option (B) is correct.

    Question:12

    The number obtained on rationalizing the denominator of \frac{1}{\sqrt{7}-2} is :
    (A) \frac{\sqrt{7}+2}{3}
    (B)\frac{\sqrt{7}-2}{3}
    (C)\frac{\sqrt{7}+2}{5}
    (D)\frac{\sqrt{7}+2}{45}

    Answer:

    Answer. [A]
    Solution    .
    We have, \frac{1}{\sqrt{7}-2}
    We have to rationalize it
    \frac{1}{\sqrt{7}-2}\times \frac{\sqrt{7}+2}{\sqrt{7}+2} [Multiplying numerator and denominator by \sqrt{7}+2]
    = \frac{\sqrt{7}+2}{\left ( \sqrt{7} \right )^{2}-\left ( 2 \right )^{2}} [\because (a – b) (a + b) = a2 – b2]
    = \frac{\sqrt{7}+2}{7-4}
    = \frac{\sqrt{7}+2}{3}
    Hence option A is correct.

    Question:13

    \frac{1}{\sqrt{9}-\sqrt{8}} is equal to :
    (A) \frac{1}{2}\left ( 3-2\sqrt{2} \right )
    (B) \frac{1}{3+2\sqrt{2}}
    (C)3-2\sqrt{2}
    (D) 3+2\sqrt{2}

    Answer:

    Answer.[D]
    Solution.
    We have, \frac{1}{\sqrt{9}-\sqrt{8}}
    We have to rationalize it
    \frac{1}{\sqrt{9}-\sqrt{8}}\times \frac{\sqrt{9}+\sqrt{8}}{\sqrt{9}+\sqrt{8}} [Multiplying and dividing by \sqrt{9}+\sqrt{8}]
    = \frac{\sqrt{9}+\sqrt{8}}{\left ( \sqrt{9} \right )^{2}-\left ( \sqrt{8} \right )^{2}} [\because (a – b) (a + b) = a2 – b2]
    =\frac{3+2\sqrt{2}}{9-8}
    = 3+2\sqrt{2}
    Hence option D is correct.

    Question:14

    After rationalizing the denominator of \frac{7}{3\sqrt{3}-2\sqrt{2}} we get the denominator as:
    (A)13
    (B)19
    (C)5
    (D)35

    Answer:

    Answer. [B]
    Solution.
    We have,\frac{7}{3\sqrt{3}-2\sqrt{2}}
    We have to rationalize it
    \frac{7}{3\sqrt{3}-2\sqrt{2}}\times \frac{3\sqrt{3}+2\sqrt{2}}{3\sqrt{3}+2\sqrt{2}}
    [Multiplying numerator and denominator by 3\sqrt{3}+2\sqrt{2}]
    = \frac{7\left ( 3\sqrt{3}+2\sqrt{2} \right )}{\left ( 3\sqrt{3} \right )^{2}-\left ( 2\sqrt{2} \right )^{2}} [\because (a – b) (a + b) = a2 – b2]
    \frac{7\left ( 3\sqrt{3} \right )+2\sqrt{2}}{27-8}
    = \frac{7\left ( 3\sqrt{3} \right )+2\sqrt{2}}{19}
    Therefore we get the denominator as 19.
    Hence (B) is the correct option.

    Question:15

    The value of \frac{\sqrt{32}+\sqrt{48}}{\sqrt{8}+\sqrt{12}} is equal to :
    (A) \sqrt{2}
    (B) 2
    (C)4
    (D) 8

    Answer:

    Answer. [B]
    Solution.
    \sqrt{32}+\sqrt{48}= \sqrt{16\times 2}+\sqrt{16\times3}= 4\left ( \sqrt{2}+\sqrt{3} \right )
    \sqrt{8}+\sqrt{12}= \sqrt{4\times 2}+\sqrt{4\times3}= 2\left ( \sqrt{2}+\sqrt{3} \right )
    \frac{\sqrt{32}+\sqrt{48}}{\sqrt{8}+\sqrt{12}}= \frac{4\left ( \sqrt{2}+\sqrt{3} \right )}{2\left ( \sqrt{2} \right )+\sqrt{3}}= 2
    Hence (B) is the correrct option.

    Question:16

    If \sqrt{2}= 1\cdot 4142 = 1.4142 then \sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}} is equal to :
    (A)2.4142
    (B)5.8282
    (C)0.4142
    (D)0.1718

    Answer:

    Answer. [C]
    Solution
    We have, \sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}
    We have to rationalize it
    \sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}\times \frac{\sqrt{2}-1}{\sqrt{2}-1}} [Multiplying numerator and denominator by \sqrt{2}-1]
    = \frac{\sqrt{\left ( \sqrt{2}-1 \right )\times\left ( \sqrt{2} -1\right ) }}{\sqrt{\left ( \sqrt{2} \right )^{2}-\left ( 1 \right )^{2}}} [\because (a – b) (a + b) = a2 – b2]
    = \frac{\sqrt{\left ( \sqrt{2}-1 \right )^{2}}}{1}
    \sqrt{\left ( \sqrt{2}-1 \right )^{2}}
    =\sqrt{2}-1
    =1\cdot 4142-1
    =0.4142
    Hence option C is correct.

    Question:17

    \sqrt[4]{\sqrt[3]{2^{2}}} equals :-
    (A) 2^{-\frac{1}{6}}
    (B)2-6
    (C) 2^{\frac{1}{6}}
    (D) 2^{6}

    Answer:

    Answer. [C]
    Solution.
    We have, \sqrt[4]{\sqrt[3]{2^{2}}} =\left ( \left ( 2^{2} \right )^{}\frac{1}{3} \right )^{\frac{1}{4}}
    \because \sqrt[n]{a}= \left ( a \right )^{\frac{1}{n}}
    \because \left ( a^{m} \right )^{n}= a^{m\times n}
    So we get,
    \left ( 2 \right )^{2\times \frac{1}{3}\times \frac{1}{4}}
    = \left ( 2 \right )^{\frac{1}{3}\times \frac{1}{2}}
    = \left ( 2 \right )^{\frac{1}{6}}
    Hence option C is correct.

    Question:18

    The product \sqrt[3]{2}.\sqrt[4]{2}.\sqrt[12]{32} equals:
    (A)\sqrt{2}
    (B)2
    (C)12\sqrt{2}
    (D)12\sqrt{32}
    Answer:

    Answer. [B]
    Solution.
    We have, \sqrt[3]{2}.\sqrt[4]{2}.\sqrt[12]{32}
    We know that \sqrt[n]{a}= \left ( a \right )^{\frac{1}{n}}
    \sqrt[3]{2}.\sqrt[4]{2}.\sqrt[12]{32}=\left ( 2 \right )^{\frac{1}{3}}\left ( 2 \right )^{\frac{1}{4}}\left ( 2\cdot 2\cdot 2\cdot 2\cdot 2 \right )^{\frac{1}{12}}
    = \left ( 2 \right )^{\frac{1}{3}}\left ( 2 \right )^{\frac{1}{4}}\left ( 2^{5} \right )^{\frac{1}{12}}
    = \left ( 2 \right )^{\frac{1}{3}}\left ( 2 \right )^{\frac{1}{4}}\left ( 2 \right )^{\frac{5}{12}} \because \left ( a^{m} \right )^{n}= a^{m\times n}
    = \left ( 2 \right )^{\frac{1}{3}+ \frac{1}{4}+\frac{5}{12}}
    \because a^{m}\times a^{n}= a^{m+n}
    Now, \frac{1}{3}+\frac{1}{4}+\frac{5}{12}= \frac{4+3+5}{12}= \frac{12}{12}= 1
    So, \left ( 2 \right )^{\frac{1}{3}+\frac{1}{4}+\frac{5}{12}}=2^{1}= 2
    Hence option B is correct.

    Question:19

    The value of \sqrt[4]{\left ( 81 \right )^{-2}}is :
    (A)\frac{1}{9}
    (B)\frac{1}{3}
    (C)9
    (D)\frac{1}{81}

    Answer:

    Answer. [A]
    Solution.
    We have, \sqrt[4]{\left ( 81 \right )^{-2}}
    We know that \sqrt[n]{a}= \left ( a \right )^{\frac{1}{n}}
    So,
    \sqrt[4]{\left ( 81 \right )^{-2}}= \left ( \left ( 81 \right )^{-2} \right )^{\frac{1}{4}}
    =\left ( 81 \right )^{-2\times \frac{1}{4}} \because \left ( a^{m} \right )^{n}= a^{m\times n}
    = 81^{-\frac{1}{2}}= \left ( \frac{1}{81} \right )^{\frac{1}{2}} \because \left ( a^{-m}= \left ( \frac{1}{a} \right )^{m} \right )
    = \sqrt{\frac{1}{81}}
    =\frac{1}{9}
    Hence option A is correct

    Question:20

    Value of (256)0.16 × (256)0.09 is :
    (A) 4
    (B) 16
    (C) 64
    (D) 256.25

    Answer:

    Answer. [A]
    Solution.     We have,
    (256)0.16 × (256)0.09 [\because am × an = am+n]
    = (256)0.16 + 0.09
    = (256)0.25
    = \left ( 256 \right )^{\frac{25}{100}}
    = \left ( 256 \right )^{\frac{1}{4}}
    Now 256 = 28 = (22)4 = 44
    = (44)1/4 [\because (am)n = amn]
    = 4
    Hence option A is correct.

    Question:21

    Which of the following is equal to x?
    (A)x^{\frac{12}{7}}+x^{\frac{5}{7}}
    (B)\sqrt[12]{\left ( x^{4} \right )^{\frac{1}{3}}}
    (C)\left ( \sqrt{x^{3}} \right )^{\frac{2}{3}}
    (D)x^{\frac{12}{7}}\times x^{\frac{7}{12}}

    Answer:

    Answer. [C]
    Solution.
    (A) We have,
    x^{\frac{12}{7}}+x^{\frac{5}{7}}= x^{\frac{1}{7}\left ( 12 \right )}+x^{\frac{1}{7}\left ( 5 \right )}
    = x^{\frac{1}{7}}\left ( x^{12} +x^{5}\right )\neq x
    (B) We have,
    \sqrt[12]{\left ( x^{4} \right )^{\frac{1}{3}}}=\left ( \left ( x^{4} \right ) ^{\frac{1}{3}}\right )^{\frac{1}{12}} \left ( \sqrt[n]{a} = \left ( a \right )^{\frac{1}{n}}\right )
    = x^{4\times ^{\frac{1}{3}\times \frac{1}{12}}}= x^{\frac{1}{9}} \because \left ( a^{m} \right )^{n}= a^{m\times n}
    \neq x
    (C) We have,
    \left ( \sqrt{x^{3}} \right )^{\frac{2}{3}}= \left ( \left ( x^{3} \right ) ^{\frac{2}{3}}\right )^{\frac{1}{2}} \left ( \sqrt[n]{a} = \left ( a \right )^{\frac{1}{n}}\right )
    = x^{3\times \frac{2}{3}\times \frac{1}{2}} \because \left ( a^{m} \right )^{n}= a^{m\times n}
    = x
    (D) We have,
    x^{\frac{12}{7}}\times x^{\frac{7}{12}}= x^{\frac{12}{7}+\frac{7}{12}}= x^{\frac{144+49}{84}}\neq x
    \because a^{m}\times a^{n}= a^{m+n}
    Hence option C is correct.

    NCERT Exemplar Maths Solutions Class 9 Chapter 1: Exercise-1.2

    Question:1

    Let x and y be rational and irrational number respectively. Is x + y necessarily an irrational number?
    Give an example in support of your answer.

    Answer:

    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Given that x and y be rational and irrational number respectively.
    So, (x + y) is necessarily an irrational number.
    For example, let x=2,y=\sqrt{3}
    Then, x + y = 2+\sqrt{3}
    If possible, let us assume x + y = 2+\sqrt{3} be a rational number.
    Consider a = 2 + \sqrt{3}
    On squaring both sides, we get
    a^{2}=(2+\sqrt{3})^{2}     (using identity (a + b)^{2} = a^{2} + b^{2} + 2ab)
    \Rightarrow a^{2}=2^{2}+(\sqrt{3})^{2}+2(2)(\sqrt{3})
    \Rightarrow a^{2}=4+3+4\sqrt{3}
    \Rightarrow \frac{a^{2}-7}{4}=\sqrt{3}
    But we have assumed a is rational
    \Rightarrow \frac{a^{2}-7}{4}is rational
    \Rightarrow \sqrt{3} is rational which is not true.
    Hence our assumption was incorrect, so 2+ \sqrt{3}is irrational.
    Hence proved

    Question:2

    Let x be rational and y be irrational. Is xy necessarily irrational? Justify your answer by an example.

    Answer:

    Answer: [xy is not necessarily an irrational number.]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Given that x and y be rational and irrational number respectively.
    Let x = 0 (a rational number) and y=\sqrt{3}be an irrational number. then,
    xy=0(\sqrt{3})=0, which is not an irrational number.
    Hence, xy is not necessarily an irrational number.

    Question:3

    (i) State whether the given statement is true or false? Justify your answer by an example. \frac{\sqrt{2}}{3} is a rational number.
    (ii) State whether the given statement is true or false? Justify your answer by an example. There are infinitely many integers between any two integers.
    (iii) State whether the given statement is true or false? Justify your answer by an example. Number of rational numbers between 15 and 18 is finite.
    (iv) State whether the given statement is true or false? Justify your answer by an example. There are numbers which cannot be written in the form \frac{p}{q} ,q \neq 0, p and q both are integers.

    (v) State whether the given statement is true or false? Justify your answer by an example. The square of an irrational number is always rational.
    (vi) State whether the given statement is true or false? Justify your answer by an example. \frac{\sqrt{12}}{\sqrt{3}} is not a rational number as \sqrt{12} and \sqrt{3} are not integers.
    (vii) State whether the given statement is true or false? Justify your answer by an example. \frac{\sqrt{15}}{\sqrt{3}}is written in the form \frac{p}{q}, q \neq 0and so it is a rational number.

    Answer:

    (i)
    Answer: False
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Examples: 4/5, 2/3, -6/7
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    Examples: \sqrt{2},\sqrt{3},\pi
    The given number is \frac{\sqrt{2}}{3}.
    Here \sqrt{2} is an irrational number and 3 is a rational number, we know that when we divide irrational number by non-zero rational it always gives an irrational number.
    Hence the given number is irrational.
    Therefore the given statement is False.

    (ii)
    Answer: False
    Solution.
    An integer is a number which can be written without fractional components or decimal representation. They can be positive, negative or zero.
    Examples: \left \{ .....-4,-3,-2,-1,0,1,2,3,4,..... \right \}
    The given statement is “There are infinitely many integers between any two integers.”
    This is false, because between two integers (like 1 and 9), there does not exist infinite integers.
    Also, if we consider two consecutive integers (like 8 and 9), there does not exist any integer between them.
    Therefore the given statement is False.

    (iii)
    Answer: False
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. So it is basically a fraction with non-zero denominator.
    Examples: 4/5, 2/3, -6/7
    So, it is a type of real number.
    The given statement is: Number of rational numbers between 15 and 18 is finite.
    If we see the definition of rational numbers as mentioned above, the given statement is false, because between any two rational numbers there exist infinitely many rational numbers.
    Here we have rational numbers between 15 and 18 as:
    16,16.1\left ( =\frac{161}{10} \right ),16.2\left ( =\frac{162}{10} \right ),16.12\left ( =\frac{1612}{100} \right ),..... and infinitely more.
    Therefore the given statement is False.

    (iv) Answer: True,
    Solution:
    There are infinitely many numbers which cannot be written in the form \frac{p}{q} ,q \neq 0, p and q both are integers. These numbers are called irrational numbers
    (v)
    Answer: False
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    The given statement is: The square of an irrational number is always rational.
    This is False, e.g., let us consider irrational numbers \sqrt{2} and \sqrt[4]{2}
    (a)(\sqrt{2})^{2}=2,which is a rational number.
    (b)(\sqrt[4]{2})^{2}=\sqrt{2}, which is an irrational number.
    Hence, square of an irrational number is not always a rational number.
    Therefore the given statement is False.
    (vi)
    Answer: False
    Solution:
    \frac{\sqrt{12}}{\sqrt{3}}=\frac{\sqrt{4 \times 3}}{\sqrt{3}}=\frac{\sqrt{4} \times \sqrt{3}}{\sqrt{3}}=2 \times 1=2which is a rational number.
    (vii)
    Answer: False
    Solution:
    \frac{\sqrt{15}}{\sqrt{3}}=\frac{\sqrt{5 \times 3}}{\sqrt{3}}=\frac{\sqrt{5} \times \sqrt{3}}{\sqrt{3}}=\sqrt{5}which is an irrational number.

    Question:4

    (i) Classify the given number as rational or irrational with justification.\sqrt{196}.
    (ii) Classify the given number as rational or irrational with justification 3\sqrt{18}
    (iii) Classify the given number as rational or irrational with justification.\sqrt{\frac{9}{27}}
    (iv) Classify the given number as rational or irrational with justification.\frac{\sqrt{28}}{\sqrt{343}}
    (v) Classify the given number as rational or irrational with justification.-\sqrt{0\cdot 4}
    (vi) Classify the given number as rational or irrational with justification.\frac{\sqrt{12}}{\sqrt{75}}
    (vii) Classify the given number as rational or irrational with justification.0.5918
    (viii) Classify the given number as rational or irrational with justification.\left ( 1+\sqrt{5} \right )-\left ( 4+\sqrt{5} \right )
    (ix) Classify the given number as rational or irrational with justification.10.124124 ………..
    (x) Classify the given number as rational or irrational with justification.1.010010001 ………….

    Answer:

    (i)Answer. [Rational]
    Solution.
    We have,
    \sqrt{196} = 14 = \frac{14}{1} which follows rule of rational number.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.

    So, \sqrt{196} is a rational number.

    (ii)Answer. [Irrational]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    We have,
    3\sqrt{18}= 3\sqrt{9\times 2}
    = 3\sqrt{9}\sqrt{2}
    = 3\times 3\sqrt{2}= 9\sqrt{2}
    So, it can be written in the form of \frac{p}{q} as \frac{9\sqrt{2}}{1}
    But we know that 9\sqrt{2} is irrational
    (Irrational numbers are real numbers which cannot be represented as simple fractions.)
    Hence, 3\sqrt{18} is an irrational number
    (iii)Answer. [Irrational]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    We have,
    \sqrt{\frac{9}{27}}= \sqrt{\frac{3\times 3}{3\times 3\times 3}}
    = \sqrt{\frac{1}{3}}= \frac{\sqrt{1}}{\sqrt{3}}= \frac{1}{\sqrt{3}}
    So this can be written in the form of \frac{p}{q} as \frac{1}{\sqrt{3}} but we can see that \sqrt{3} (denominator) is irrational.
    (Irrational numbers are real numbers which cannot be represented as simple fractions.)
    Hence \sqrt{\frac{9}{27}} is irrational

    (iv)Answer. [Rational]
    Solution.
    We have,
    \frac{\sqrt{28}}{\sqrt{343}}= \frac{\sqrt{4\times 7}}{\sqrt{49\times 7}}
    = \frac{2\times \sqrt{7}}{7\times \sqrt{7}}= \frac{2}{7}
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Hence \frac{\sqrt{28}}{\sqrt{343}} is a rational number.
    (v)Answer. [Irrational]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    We have,
    -\sqrt{0\cdot 4}= -\sqrt{\frac{4}{10}}
    = -\sqrt{\frac{2}{5}}= -\frac{\sqrt{2}}{\sqrt{5}}
    So, it can be written in the form of \frac{p}{q} as \frac{-\sqrt{2}}{\sqrt{5}}
    But we know that both \sqrt{2},\sqrt{5} are irrational
    (Irrational numbers are real numbers which cannot be represented as simple fractions.)
    Hence, -\sqrt{0\cdot 4} is an irrational number

    (vi)Answer. [Rational]
    Solution.
    We have,
    \frac{\sqrt{12}}{\sqrt{75}}= \frac{\sqrt{4\times 3}}{\sqrt{25\times 3}}
    = \frac{\sqrt{4}\sqrt{3}}{\sqrt{25}\sqrt{3}}= \frac{\sqrt{4}}{\sqrt{25}}
    = \frac{2}{5}
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q
    should be rational when the fraction is expressed in the simplest form.
    So, \frac{\sqrt{12}}{\sqrt{75}} is a rational number.
    (vii)Answer. [Rational]
    Solution.
    We have,
    0\cdot 5918= \frac{0\cdot 5918\times 10000}{1\times 10000}
    = \frac{5918}{10000}= \frac{2959}{5000}
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Also we can see that 0.5918 is a terminating decimal number hence it must be rational.
    So, 0.5918 is a rational number.
    (viii)Answer. [Rational]
    Solution.
    We have,
    \left ( 1+\sqrt{5} \right )-\left ( 4+\sqrt{5} \right )
    = 1+\sqrt{5}-4-\sqrt{5}
    = -3= \frac{-3}{1}
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    So, \left ( 1+\sqrt{5} \right )-\left ( 4+\sqrt{5} \right ) is a rational number.

    (ix)Answer. [Rational]
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    All non-terminating recurring decimal numbers are rational numbers.
    Non terminating Recurring decimals are those decimals which have a particular pattern/sequence that keeps on repeating
    itself after the decimal point. They are also called repeating decimals.
    Examples: 1/3 = 0.33333…, 4/11 = 0.363636…
    Now, 10.124124 ………. is a decimal expansion which is a non-terminating recurring.
    So, it is a rational number.
    (x)Answer. [Irrational]
    Solution    .
    Non terminating Recurring decimals are those decimals which have a particular pattern/sequence that keeps on repeating itself after the decimal point.
    All non-terminating recurring decimal numbers are rational numbers.
    Non terminating Non Recurring decimals are those decimals which do not have a particular pattern/sequence after the decimal point and it does not end.
    All non-terminating non-recurring decimal numbers are irrational numbers.
    1.010010001 ………. is non-terminating non-recurring decimal number, therefore it cannot be written in the form \frac{p}{q};q\neq 0,with p,q both as integers.
    Thus, 1.010010001 ……….. is an irrational number.

    NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.3

    Question:1

    (i)Find whether variable x represent rational number or an irrational number.x2 = 5
    (ii)Find whether variable x represent rational number or an irrational number.y2 = 9
    (iii)Find whether variable x represent rational number or an irrational number.z2 = 0.04
    (iv)Find whether variable x represent rational number or an irrational number.u2 = \frac{17}{4}

    Answer:

    (i)Answer. [Irrational]
    Solution.
    Given that
    x2 = 5
    On taking square root on both sides, we get
    \Rightarrow x= \pm \sqrt{5}
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    So, x is an irrational number

    (ii)Answer. [Rational]
    Solution.
    We have
    y2 = 9
    On taking square root on both sides, we get
    \Rightarrow x= \pm 3
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q
    should be rational when the fraction is expressed in the simplest form.
    So, y can be written as \frac{3}{1},\frac{-3}{1} where 1, 3, -3 are rational numbers.
    Hence y is rational.
    (iii)Answer. [Rational]
    Solution.
    We have
    z2 = 0.04 =\frac{4}{100}
    On taking square root on both sides, we get
    \Rightarrow z= \pm \frac{2}{10}= \pm \frac{1}{5}
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q
    should be rational when the fraction is expressed in the simplest form.
    So, z can be written as \pm \frac{1}{5} where 1, 5, -5 are rational numbers.
    Hence z is rational.
    (iv)Answer. [Irrational]
    Solution.
    Given that
    u2 = \frac{17}{4}
    On taking square root on both sides, we get
    \Rightarrow u= \sqrt{\frac{17}{4}}= \pm \frac{\sqrt{17}}{2}
    Any number which can be represented in the form of p/q where q is not equal to zero
    is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    So, u can be written as \pm \frac{\sqrt{17}}{2} where \sqrt{17} is irrational.
    Hence u is irrational.

    Question:2

    (i) Find three rational numbers between – 1 and – 2
    (ii) Find three rational numbers between 0.1 and 0.11
    (iii)Find three rational numbers between \frac{5}{7} and \frac{6}{7}
    (iv)Find three rational numbers between \frac{1}{4} and \frac{1}{5}

    Answer:

    (i)Answer.
    -\frac{11}{10}, -\frac{6}{5}    and-\frac{5}{4}
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.

    Between -1 and -2, many rational number can be written as:
    -1\cdot 1=-\frac{11}{10}
    -1\cdot 2=-\frac{12}{10}= -\frac{6}{5}
    -1\cdot 25=-\frac{125}{100}= -\frac{5}{4}
    -1\cdot 3=-\frac{13}{10}
    -1\cdot 4=-\frac{14}{10}= -\frac{7}{5}
    (ii) Answer: \frac{103}{1000},\frac{104}{1000},\frac{105}{1000}
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.

    Between 0.1 and 0.11, many rational number can be written as:

    0.103 = \frac{103}{1000}

    0.104 = \frac{104}{1000}

    0.105 = \frac{105}{1000}


    (iii)Answer. \frac{51}{70},\frac{52}{70}and\frac{53}{70}
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    We can write \frac{5}{7}as \frac{5\times 10}{7\times 10}= \frac{50}{70} and \frac{6}{7} as \frac{6\times 10}{7\times 10}= \frac{60}{70}
    So, three rational number between \frac{5}{7}and\frac{6}{7} are \frac{51}{70},\frac{52}{70}and\frac{53}{70}

    (iv)Answer. \frac{41}{200},\frac{42}{200},\frac{43}{200}
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    L.C.M. of 4 and 5 is 20.
    We can write \frac{1}{4} as \frac{1\times 40}{4\times 50}= \frac{50}{200}
    and \frac{1}{5}\, as\, \frac{1\times 40}{5\times 40}= \frac{40}{200}
    So, three rational number between \frac{1}{4}\, and\,\frac{1}{5} are
    \frac{41}{200},\frac{42}{200},\frac{43}{200}

    Question:3

    (i)Insert a rational number and an irrational number between the following. 2 and 3
    (ii)Insert a rational number and an irrational number between the following.0.1 and 0.1
    (iii)Insert a rational number and an irrational number between the following.\frac{1}{3}\, and\, \frac{1}{2}
    (iv)Insert a rational number and an irrational number between the following.\frac{-2}{5}\, and\, \frac{1}{2}
    (v)Insert a rational number and an irrational number between the following.0.15 and 0.16
    (vi)Insert a rational number and an irrational number between the following.\sqrt{2} and \sqrt{3}
    (vii)Insert a rational number and an irrational number between the following.2.357 and 3.121
    (viii)Insert a rational number and an irrational number between the following..0001 and .001
    (ix)Insert a rational number and an irrational number between the following.3.623623 and 0.484848
    (x) Insert a rational number and an irrational number between the following.6.375289 and 6.375738
    Answer:

    (i) Answer. Rational number: \frac{5}{2}
    Irrational number: 2.040040004 ……….
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 2 and 3
    Rational number: 2.5 = \frac{25}{10}= \frac{5}{2}
    and irrational number : 2.040040004

    (ii) Answer. Rational number: \frac{19}{1000}
    Irrational number 0.0105000500005 ……..
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 0 and 0.1:
    0.1 can be written as 0.10
    Rational number: 0.019 = \frac{19}{1000}
    and irrational number 0.0105000500005

    (iii)Answer. Rational number \frac{21}{60}
    Irrational number : 0.414114111 ……
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions. They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    LCM of 3 and 2 is 6.
    We can write \frac{1}{3} as \frac{1\times 20}{3\times 20}= \frac{20}{60}
    and \frac{1}{2} as \frac{1\times 30}{3\times 30}= \frac{30}{60}
    Also, \frac{1}{3} = 0.333333….
    And \frac{1}{2}= 0\cdot 5
    So, rational number between \frac{1}{3} and \frac{1}{2} is \frac{21}{60}
    and irrational number : 0.414114111 ……

    (iv)Answer. Rational number: 0
    Irrational number: 0.151551555 …….
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    \frac{-2}{5}= -0\cdot 4 and \frac{1}{2}= -0\cdot 5
    Rational number between -0.4 and 0.5 is 0
    And irrational number: 0.151551555 …….
    (v) Answer. Rational number: \frac{151}{1000}
    Irrational number: 0.151551555 ……….
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 0.15 and 0.16
    Rational number : 0.151 = \frac{151}{1000}
    and irrational number 0.151551555

    (vi) Answer. Rational number: \frac{3}{2}
    Irrational number: 1.585585558 ………
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions. They are non-terminating non-recurring in nature.
    Between \sqrt{2}\, and\, \sqrt{3}
    \sqrt{2}= 1\cdot 414213562373
    \sqrt{3}= 1\cdot 732050807568
    Rational number: 1.5 = \frac{3}{2}
    and irrational number: 1.585585558

    (vii) Answer. Rational number: 3
    Irrational number: 3.101101110………
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 2.357 and 3.121
    Rational number: 3
    Irrational number: 3.101101110………
    (viii) Answer. Rational number: \frac{2}{10000}
    Irrational number: 0.000113133133 ……….
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 0.0001 and 0.001
    Rational number: 0.0002 = \frac{2}{10000}
    Irrational number: 0.000113133133

    (ix) Answer. Rational number: 1
    Irrational number: 1.909009000 ……
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 3.623623 and 0.484848
    A rational number between 3.623623 and 0.484848 is 1.
    An irrational number between 3.623623 and 0.484848 is 1.909009000 ……

    (x) Answer. A rational number is \frac{63753}{10000}
    An irrational number is 6.375414114111……..
    Solution.
    Any number which can be represented in the form of p/q where q is not equal to zero is a rational number. Also, both p and q should be rational when the fraction is expressed in the simplest form.
    Irrational numbers are real numbers which cannot be represented as simple fractions.
    They are non-terminating non-recurring in nature. It means they keep on continuing after decimal point and do not have a particular pattern/sequence after the decimal point.
    Between 6.375289 and 6.375738:
    A rational number is 6.3753 = \frac{63753}{10000}
    An irrational number is 6.375414114111……..

    Question:4

    Represent the following numbers on the number line. 7, 7.2, -\frac{3}{2},-\frac{12}{5}

    Answer:

    Solution.
    Firstly we draw a number line whose mid-point is O. Mark positive numbers on right hand side of O and negative numbers on left hand side of O.
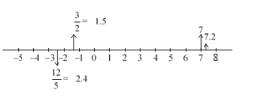
    FireShot%20Capture%20003%20-%20Careers360%20CMS%20-%20cms-article%20-%20learn(i) Number 7 is a positive number. So we mark a number 7 on the right
    hand side of O, which is at a 7 units distance form zero.
    (ii) Number 7.2 is a positive number. So, we mark a number 7.2 on the right hand side of O, which is 7.2 units distance from zero.
    (iii) Number -\frac{3}{2} or – 1.5 is a negative number so, we mark a number 1.5 on the left hand side of zero, which is at 1.5 units distance from zero.
    (iv) Number -\frac{12}{5} or –2.4 is a negative number. So, we mark a number 2.4 on the left hand side of zero, which is at 2.4 units distance from zero.

    Question:5

    Locate \sqrt{5},\sqrt{10} and \sqrt{17} on the number line

    Answer:

    Hint.
    Solution.
    Step I- Draw number line shown in the figure.
    Let the point O represent 0 (zero) and point A represent 2 units from O.
    58373
    Step II- Draw perpendicular AX from A on the number line and cut off arc AB = 1 unit
    We have OA = 2 units and AB = 1 unit
    Using Pythagoras theorem, we have.
    OB2 = OA2 + AB2
    OB2 = (2)2 + (1)2 = 5
    OB = \sqrt{5}
    Taking O as the centre and OB = \sqrt{5} as radius draw an arc cutting the line at C.
    Clearly, OC = OB = \sqrt{5}.
    Hence, C represents \sqrt{5} on the number line.
    Similarly for \sqrt{10} and \sqrt{17}we can plot the points as follows:
    \sqrt{10}= \sqrt{3^{2}+1^{2}}
    \sqrt{17}= \sqrt{4^{2}+1^{2}}
    583731
    583732

    Question:6

    (i) Represent geometrically the following numbers on the number line : \sqrt{4\cdot 5}
    (ii) Represent geometrically the following numbers on the number line : \sqrt{5\cdot 6}
    (iii) Presentation of \sqrt{8\cdot 1} on number line :
    (iv) Presentation of \sqrt{2\cdot 3} on number line:

    Answer:

    (i) Solution. AB = 4.5 units, BC = 1 unit
    58395
    OC = OD = \frac{5\cdot 5}{2} = 2.75 units
    OD2 = OB2 + BD2
    \left ( \frac{4\cdot 5}{2} \right )^{2}= \left ( \frac{4\cdot 5}{2} -1\right )^{2}+\left ( BD \right )^{2}
    \Rightarrow BD^{2}= \left ( \frac{4\cdot 5+1}{2} \right )^{2}- \left ( \frac{4\cdot 5-1}{2} \right )^{2}
    \Rightarrow BD^{2}= 4. 5
    \Rightarrow BD= \sqrt{4. 5}
    So the length of BD will be the required one so mark an arc of length BD on number line, this will result in the required length.

    (ii) Solution. Presentation of \sqrt{5. 6}on number line.
    Mark the distance 5.6 units from a fixed point A on a given line to obtain a point B such that AB = 5.6 units. From B mark a distance of 1 unit and mark a new point C. Find the mid point of AC and mark that point as O. Draw a semicircle with center O and radius OC. Draw a line
    perpendicular to AC passing through B and intersecting the semicircle at O. Then BD = \sqrt{5\cdot 6}

    583951
    (iii) Solution
    Mark the distance 8.1 units from a fixed point A on a given line to obtain a point B such that AB = 8.1 units. From B mark a distance of 1 unit and mark the new point AB. Find the mid point of AC and mark a point as O. Draw a semi circle with point O and radius OC. Draw a line perpendicular to AC passing through B and intersecting
    the semicircle at D. Then BD -     \sqrt{8. 1}
    583952
    (iv) Solution
    Mark the distance 2.3 unit from a fixed point A on a given line. To obtain a point B such that AB = 2.3 units. From B mark a distance of 1 unit and mark a new point as C. Find the mid point of AC and mark the point asO. Draw a line perpendicular to AC passing through B and intersecting the semicircle at D. Then BD = \sqrt{2. 3}
    583953

    Question:7

    (i) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0. 0.2
    (ii) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0.
    0.888…….
    (iii) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0.5.\bar{2}
    (iv) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0.0\cdot \overline{001}
    (v) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0.0.2555……
    (vii) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0..00323232…..
    (viii) Express the following in the form \frac{p}{q}, where p and q are integers and q\neq 0..404040……..

    Answer:

    (i) Answer.\frac{1}{5}
    Solution. We know that
    0.2 can be written as \frac{2}{10}
    Now,
    \frac{2}{10}= \frac{1}{5}
    Hence the answer is \frac{1}{5}

    (ii) Answer.\frac{8}{9}
    Solution. Let x = 0.888….. .…(i)
    Multiply RHS and LHS by 10
    10 x = 8.88……. …(ii)
    Subtracting equation (i) from (ii)
    We get
    10x – x = 8.8 – 0.8
    \Rightarrow 9x= 8
    \Rightarrow x= \frac{8}{9}
    Hence answer is \frac{8}{9}

    (iii) Answer.\frac{47}{9}
    Solution. Let x = 5\cdot \bar{2} …eq. (1)
    Multiply by 10 on both sides
    10x = 52\cdot \bar{2} …eq (2)
    Subtracting equation (1) from (2)
    We get
    10x – x = 52\cdot \bar{2} – 5\cdot \bar{2}
    \Rightarrow 9x = 47
    \Rightarrow x = \frac{47}{9}
    Hence the answer is \frac{47}{9}

    (iv) Answer.\frac{1}{999}
    Solution. Let x = 0\cdot \overline{001} …. Eq. (1)
    Multiply by 1000 on both sides
    1000 x = 1\cdot \overline{001} …eq.(2)
    Subtracting eq. (1) from (2)
    We get
    1000 x – x = 1\cdot \overline{001} – 1\cdot \overline{001}
    \Rightarrow 999x = 1
    \Rightarrow x = \frac{1}{999}
    Hence the answer is \frac{1}{999}
    (v) Answer.\frac{23}{90}
    Solution. Let x = 0.2555 ….. …eq.(1)
    Multiply by 10 on both sides
    10x = 2.555… …eq.(2)
    Multiply by 100 on both sides
    100x = 25.55… …eq. (3)
    Subtracting eq. (2) from (3),
    We get
    100x – 10x = 25.555… – 2.555…
    \Rightarrow 90x = 23
    \Rightarrow x = \frac{23}{90}
    Hence the answer is \frac{23}{90}

    (vii) Answer.\frac{8}{2475}
    Solution. Let x = 0.00323232….. …eq.(1)
    Multiply with 100 on both sides.
    We get
    100x = 0.3232… …eq(2)
    Multiply again with 100 on both sides,
    10000x = 32.3232… …eq(3)
    Equation (3) – (2)
    we get,
    10000 x – 100x = 32.3232… – 0.3232…
    \Rightarrow 9900x = 32
    \Rightarrow x = \frac{32}{9900}
    x = \frac{8}{2475}
    Hence the answer is \frac{8}{2475}

    (viii) Answer.\frac{40}{99}
    Solution. Let x = 0.404040……. …(1)
    Multiplying by 100 on both sides
    we get
    100x = 40.40… …(2)
    Subtracting equation (1) from (2)
    we get
    100x – x = 40.40 – 0.40
    \Rightarrow99x = 40
    \Rightarrow x = \frac{40}{99}
    Hence the answer is \frac{40}{99}

    Question:8

    Show that 0.142857142857 ……. = \frac{1}{7}

    Answer:

    Solution. Let, x = 0.142857142857… …(i)
    Multiply (i) by 1000000, we get
    1000000 x = 142857.142857… …(ii)
    Subtracting equation (i) from (ii), we get
    1000000 x – x = 142857.142857… - 0.142857…
    999999 x = 142857
    x= \frac{142857}{999999}= \frac{47619}{333333}= \frac{15873}{111111}= \frac{5291}{37037}
    = \frac{481}{3367}= \frac{1}{7}
    Hence, 0.142857 ……. \frac{1}{7}
    Hence proved

    Question:9

    (i) Simplify the following : \sqrt{45}-3\sqrt{20}+4\sqrt{5}
    (ii) Simplify the following : \frac{\sqrt{24}}{8}+\frac{\sqrt{54}}{9}
    (iii) Simplify the following : 4\sqrt{12}\times 7\sqrt{6}
    (iv) Simplify the following : 4\sqrt{28}\div 3\sqrt{7}\div 3\sqrt{7}
    (v) Simplify the following : 3\sqrt{3}+2\sqrt{27}+\frac{7}{\sqrt{3}}
    (vi) Simplify the following : \left ( \sqrt{3}-\sqrt{2} \right )^{2}
    (vii) Simplify the following : \sqrt[4]{81}- 8\sqrt[3]{216}+15\sqrt[5]{32}+\sqrt{255}
    (viii) Simplify the following : \frac{3}{\sqrt{8}}+\frac{1}{\sqrt{2}}
    (ix) Simplify the following : \frac{2\sqrt{3}}{3}-\frac{\sqrt{3}}{6}

    Answer:

    (i) Answer.\sqrt{5}
    Solution. \sqrt{45}-3\sqrt{20}+4\sqrt{5}
    We know that,
    45 = 3\times 3\times 5
    20 = 2\times 2\times 5
    So we get
    \sqrt{3\times3\times5 }-3\sqrt{2\times2\times5}+4\sqrt{5}
    = 3\sqrt{5}-3\left ( 2\sqrt{5} \right )+4\sqrt{5}
    = 3\sqrt{5}-6\sqrt{5}+4\sqrt{5}
    = 7\sqrt{5}-6\sqrt{5}
    = \sqrt{5}
    Hence the answer is \sqrt{5}

    (ii) Answer. \frac{7\sqrt{6}}{12}
    Solution. We have, \frac{\sqrt{24}}{8}+\frac{\sqrt{54}}{9}
    We know that,
    24= 6\times 4= 3\times 2\times 2\times 2
    54= 9\times 6= 3\times 3\times 3\times 2
    So we get
    \frac{\sqrt{24}}{8}+\frac{\sqrt{54}}{9}= \frac{2\sqrt{6}}{8}+\frac{3\sqrt{6}}{9}
    = \frac{\sqrt{6}}{4}+\frac{\sqrt{6}}{3}
    Taking LCM (3,4) = 12
    = \frac{3\sqrt{6}+4\sqrt{6}}{12}
    = \frac{7\sqrt{6}}{12}
    (iii) Answer. \sqrt[28]{2^{18} \times 3^{11}}
    Solution. We have
    \sqrt[4]{12}\times \sqrt[7]{6}
    We know that
    12 = 2\times 2\times 3
    6 = 2\times 3
    So we get,
    =\sqrt[4]{2\times 2\times 3}\times \sqrt[7]{2\times 3}
    =2^{1 / 4} \cdot 2^{1 / 4} \cdot 3^{1 / 4} \cdot 2^{1 / 7} \cdot 3^{1 / 7}
    =2^{\frac{1}{4}+\frac{1}{4}+\frac{1}{7}} \times 3^{\frac{1}{4}+\frac{1}{7}}
    =2^{9 / 14} \times 3^{11 / 28}
    =\sqrt[28]{2^{18} \times 3^{11}}
    Hence the number is \sqrt[28]{2^{18} \times 3^{11}}.

    (iv)Answer. \frac{8}{\left ( 3\times \sqrt[3]{7} \right )}
    Solution. We have, 4\sqrt{28}\div 3\sqrt{7}\div \sqrt[3]{7}
    We know that
    28 = 4\times 7
    So we can write,
    4\sqrt{28}\div 3\sqrt{7}\div \sqrt[3]{7}= \left [ \frac{4\sqrt{28}}{3\sqrt{7}} \right ]\div 7^{\frac{1}{3}}
    = \left [ \frac{4\sqrt{4\times 7}}{3\sqrt{7}} \right ]\div 7^{\frac{1}{3}}
    = \left [ \frac{4\times 2\sqrt{ 7}}{3\sqrt{7}} \right ]\div 7^{\frac{1}{3}}
    = \frac{8}{3}\div 7^{\frac{1}{3}}
    = \frac{8}{\left ( 3\times 7^{\frac{1}{3}} \right )}
    = \frac{8}{\left ( 3\times \sqrt[3]{7} \right )}
    Hence the answer is \frac{8}{\left ( 3\times \sqrt[3]{7} \right )}

    (v) Answer.3\sqrt{3}+2\sqrt{27}+\frac{7}{\sqrt{3}}
    We know that
    27 = 3\times 3\times 3
    So, 3\sqrt{3}+2\sqrt{27}+\frac{7}{\sqrt{3}} = 3\sqrt{3}+2\sqrt{3\times 3\times 3}+\frac{7}{\sqrt{3}}

    = 3\sqrt{3}+2\left ( 3\sqrt{3} \right )+\frac{7}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}
    (Rationalising the denominator)
    = 3\sqrt{3}+6\left ( \sqrt{3} \right )+\frac{7\sqrt{3}}{3}

    = \left ( 3+6+\frac{7}{3} \right )\sqrt{3} (Taking \sqrt{3} common)
    Now LCM (1,1,3) = 3
    = \left ( \frac{9+18+7}{3} \right )\sqrt{3}
    = \frac{34}{3}\sqrt{3}
    = 19\cdot 63
    Hence the answer is 19.63
    (vi) Answer.5-2\sqrt{6}
    Solution. Given, \left ( \sqrt{3}-\sqrt{2} \right )^{2}
    We know that (a + b)2 = a2 – 2ab + b2
    Comparing the given equation with the identity, we get:
    \left ( \sqrt{3}-\sqrt{2} \right )^{2}= \left ( \sqrt{3} \right )^{2}-2\left ( \sqrt{3} \right )\left ( \sqrt{2} \right )+\left ( \sqrt{2} \right )^2
    = 3 + 2 – 2\sqrt{3\times 2}
    = 5-2\sqrt{6}
    Hence the answer is 5-2\sqrt{6}

    (vii) Answer. 0
    Solution. We have, \sqrt[4]{81}-8 \sqrt[3]{216}+15\sqrt[5]{32}+\sqrt{225}
    We know that
    81 = 3\times 3\times3\times3
    216 = 6\times 6\times6
    32 = 2\times 2\times2\times2\times2
    225 = 15\times 15
    So,\sqrt[4]{81}-8 \sqrt[3]{216}+15\sqrt[5]{32}+\sqrt{225}
    = \sqrt[4]{3\times3\times3\times3 }-8\sqrt[3]{6\times6\times6}+15\sqrt[5]{2\times2\times2\times2\times2}+\sqrt{15\times15}
    = 3 – 8 × 6 + 15 × 2 + 15
    = 3 – 48 + 30 + 15
    = – 45 + 45
    = 0
    Hence the answer is 0

    (viii) Answer. \frac{5}{2\sqrt{2}}
    Solution. We have, \frac{3}{\sqrt{8}}+\frac{1}{\sqrt{2}}
    We know that, 8 =2\times 2\times 2
    So,
    \frac{3}{\sqrt{8}}+\frac{1}{\sqrt{2}} = \frac{3}{\sqrt{2\times 2\times 2}}+\frac{1}{\sqrt{2}}
    = \frac{3}{2\sqrt{2}}+\frac{1}{\sqrt{2}}
    = \frac{3}{2\sqrt{2}}+\frac{2}{2\sqrt{2}}
    = \frac{5}{2\sqrt{2}}
    Hence the answer is \frac{5}{2\sqrt{2}}

    (ix) Answer. \frac{\sqrt{3}}{2}
    Solution. We have, \frac{2\sqrt{3}}{3}-\frac{\sqrt{3}}{6}
    LCM (3,6) = 6
    \frac{2\sqrt{3}}{3}-\frac{\sqrt{3}}{6}= \frac{4\sqrt{3}}{6}-\frac{\sqrt{3}}{6}
    = \frac{4\sqrt{3}-\sqrt{3}}{6}
    = \frac{3\sqrt{3}}{6}
    = \frac{\sqrt{3}}{2}
    Hence the answer is \frac{\sqrt{3}}{2}.

    Question:10

    (i) Rationalise the denominator of the following : \frac{2}{3\sqrt{3}}
    (ii)Rationalise the denominator of the following : \frac{\sqrt{40}}{\sqrt{3}}
    (iii) Rationalise the denominator of the following : \frac{3+\sqrt{2}}{4\sqrt{2}}
    (iv)Rationalise the denominator of the following :\frac{16}{\sqrt{41}-5}
    (v) Rationalise the denominator of the following : \frac{2+\sqrt{3}}{2-\sqrt{3}}
    (vi) Rationalise the denominator of the following : \frac{\sqrt{6}}{\sqrt{2}+\sqrt{3}}
    (vii) Rationalise the denominator of the following : \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}
    (viii) Rationalise the denominator of the following : \frac{3 \sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}
    (ix) Rationalise the denominator of the following : \frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}

    Answer:

    (i) Answer.\frac{2\sqrt{3}}{9}
    Solution. We have, \frac{2}{3\sqrt{3}}
    Rationalising the denominator, we get:
    \frac{2}{3\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}
    = \frac{2\sqrt{3}}{3\sqrt{3}\sqrt{3}}
    = \frac{2\sqrt{3}}{9}
    Hence the answer is \frac{2\sqrt{3}}{9}

    (ii) Answer.\frac{2\sqrt{30}}{3}
    Solution. We have ,\frac{\sqrt{40}}{\sqrt{3}}
    We know that, 40 = (2) (2) (10)
    \frac{\sqrt{40}}{\sqrt{3}}= \frac{\sqrt{2\cdot 2\cdot 10}}{\sqrt{3}}= \frac{2\sqrt{10}}{\sqrt{3}}
    Rationalising the denominator, we get:
    = \frac{2\sqrt{10}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}
    = \frac{2\sqrt{10}\sqrt{3}}{\sqrt{3}\sqrt{3}}
    = \frac{2\sqrt{30}}{3}
    Hence the answer is: \frac{2\sqrt{30}}{3}

    (iii) Answer. \frac{3\sqrt{2}+2}{8}
    Solution. We have \frac{3+\sqrt{2}}{4\sqrt{2}}
    Rationalising the denominator, we get:
    \frac{3+\sqrt{2}}{4\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}
    = \frac{\left ( 3+\sqrt{2} \right )\sqrt{2}}{4\sqrt{2}\sqrt{2}}
    = \frac{3\sqrt{2}+2}{8}
    Hence the answer is \frac{3\sqrt{2}+2}{8}

    (iv) Answer. \sqrt{41}+5
    Solution. We have \frac{16}{\sqrt{41}-5}
    Rationalising the denominator, we get:
    \frac{16}{\sqrt{41}-5}\times \frac{\sqrt{41}+5}{\sqrt{41}+5}
    = \frac{16\left ( \sqrt{41}+5 \right )}{\left ( \sqrt{41}-5 \right )\sqrt{41}+5}
    Using the identity (a – b) (a + b) = a2 – b2
    We get:
    = \frac{16\left ( \sqrt{41}+5 \right )}{\left ( \sqrt{41} \right )^{2}-\left ( 5 \right )^{2}}
    = \frac{16\left ( \sqrt{41}+5 \right )}{41-25}
    = \frac{16\left ( \sqrt{41}+5 \right )}{16}
    = \sqrt{41}+5
    Hence the answer is \sqrt{41}+5

    (v) Answer.7+4\sqrt{3}
    Solution. We have, \frac{2+\sqrt{3}}{2-\sqrt{3}}
    Rationalising the denominator, we get:
    \frac{2+\sqrt{3}}{2-\sqrt{3}}\times \frac{2+\sqrt{3}}{2-\sqrt{3}}
    = \frac{\left ( 2+\sqrt{3} \right )^{2}}{\left ( 2-\sqrt{3} \right )\left ( 2+\sqrt{3} \right )}
    Using (a – b) (a + b) = a2 – b2
    and (a + b)2 = a2 + b2 + 2ab
    = \frac{2^{2}+\left ( \sqrt{3} \right )^{2}+2\cdot 2\cdot \sqrt{3}}{2^{2}-\left ( \sqrt{3} \right )^{2}}
    = \frac{4+3+4\sqrt{3}}{4-3}
    = 7+4\sqrt{3}
    Hence the answer is 7+4\sqrt{3}
    (vi)Answer. 3\sqrt{2}-2\sqrt{3}
    Solution. We have, \frac{\sqrt{6}}{\sqrt{2}+\sqrt{3}}
    Rationalising the denominator, we get:
    = \frac{\sqrt{6}}{\sqrt{2}+\sqrt{3}}\times \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}
    = \frac{\sqrt{6}\left ( \sqrt{3}-\sqrt{2} \right )}{\left ( \sqrt{2}+\sqrt{3} \right )\left ( \sqrt{3}-\sqrt{2} \right )}
    Using the identity (a – b) (a + b) = a2 – b2
    We get:
    = \frac{\sqrt{18}-\sqrt{12}}{\left ( \sqrt{3} \right )^{2}\left ( \sqrt{2} \right )^{2}}
    = \frac{\sqrt{3\cdot 3\cdot 2}-\sqrt{2\cdot 2\cdot 3}}{3-2}
    = \frac{3\sqrt{2}-2\sqrt{3}}{1}
    = 3\sqrt{2}-2\sqrt{3}
    Hence the answer 3\sqrt{2}-2\sqrt{3}
    (vii) Answer. 5+2\sqrt{6}
    Solution. We have, \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}
    Rationalising the denominator, we get:
    \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\times \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}
    = \frac{\left ( \sqrt{3} +\sqrt{2}\right )^{2}}{\left ( \sqrt{3} -\sqrt{2} \right )\left ( \sqrt{3} +\sqrt{2} \right )}
    Using (a – b) (a + b) = a2 – b2
    and (a + b)2 = a2 + b2 + 2ab
    = \frac{\left ( \sqrt{3} \right )^{2}+\left ( \sqrt{2} \right )^{2}+2\sqrt{3}\sqrt{2}}{\left ( \sqrt{3} \right )^{2}-\left ( \sqrt{2} \right )^{2}}
    = \frac{3+2+2\sqrt{6}}{3-2}
    = 5+2\sqrt{6}
    Hence the answer is 5+2\sqrt{6}
    (viii)
    Answer:9+2 \sqrt{15}
    Solution:
    We have \frac{3 \sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}
    Rationalize
    =\frac{3 \sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}} \times \frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{3 \sqrt{5}(\sqrt{5}+\sqrt{3})+\sqrt{3}(\sqrt{5}+\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}
    =\frac{15+3 \sqrt{15}+\sqrt{15}+3}{5-3}=\frac{18+4 \sqrt{15}}{2}
    =9+2 \sqrt{15}
    (ix) Answer:\frac{9+4 \sqrt{6}}{15}
    Solution:
    We have \frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}
    =\frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}=\frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{16 \times 3}+\sqrt{9 \times 2}}=\frac{4 \sqrt{3}+5 \sqrt{2}}{4 \sqrt{3}+3 \sqrt{2}}
    Rationalize
    =\frac{4 \sqrt{3}+5 \sqrt{2}}{4 \sqrt{3}+3 \sqrt{2}} \times \frac{(4 \sqrt{3}-3 \sqrt{2})}{(4 \sqrt{3}-3 \sqrt{2})}
    =\frac{4 \sqrt{3}(4 \sqrt{3}-3 \sqrt{2})+5 \sqrt{2}(4 \sqrt{3}-3 \sqrt{2})}{(4 \sqrt{3})^{2}-(3 \sqrt{2})^{2}}
    =\frac{48-12 \sqrt{6}+20 \sqrt{6}-30}{30}
    =\frac{18+8 \sqrt{6}}{30}
    =\frac{9+4 \sqrt{6}}{15}

    Question:11

    (i) Find the values of a in each of the following : \frac{5+2\sqrt{3}}{7+4\sqrt{3}}= a-6\sqrt{3}
    (ii) Find the values of a in the following : \frac{3-\sqrt{5}}{3+2\sqrt{5}}= a\sqrt{5}-\frac{19}{11}
    (iii) Find the values of b in the following : \frac{\sqrt{2}+\sqrt{3}}{3 \sqrt{2}-2 \sqrt{3}}=2-b \sqrt{6}
    (iv) Find the values of a and b in the following : \frac{7+\sqrt{5}}{7-\sqrt{5}}-\frac{7-\sqrt{5}}{7+\sqrt{5}}= a+\frac{7}{11}\sqrt{5b}

    Answer:

    (i) Answer. a = 11
    Solution. We have, \frac{5+2\sqrt{3}}{7+4\sqrt{3}}= a-6\sqrt{3}
    LHS = \frac{5+2\sqrt{3}}{7+4\sqrt{3}}
    Rationalising the denominator, we get:
    = \frac{5+2\sqrt{3}}{7+4\sqrt{3}}\times \frac{7-4\sqrt{3}}{7-4\sqrt{3}}
    = \frac{\left ( 5+2\sqrt{3} \right )\left ( 7-4\sqrt{3} \right )}{\left ( 7+4\sqrt{3} \right )\left ( 7-4\sqrt{3} \right )}
    {Using (a – b) (a + b) = a2 – b2}

    = \frac{35+14\sqrt{3}-20\sqrt{3}-24}{7^{2}-\left ( 4\sqrt{3} \right )^{2}}
    = \frac{11-6\sqrt{3}}{49-48}
    = 11-6\sqrt{3}
    Now RHS = a-6\sqrt{3}
    \Rightarrow 11-6\sqrt{3}= a-6\sqrt{3}
    \Rightarrow 11-6\sqrt{3}= a-6\sqrt{3}
    \Rightarrow a= 11
    Hence a = 11 is the required answer

    (ii)Answer.a= \frac{9}{11}
    Solution. Given that, \frac{3-\sqrt{5}}{3+2\sqrt{5}}= a\sqrt{5}-\frac{19}{11}
    LHS = \frac{3-\sqrt{5}}{3+2\sqrt{5}}
    Rationalising the denominator, we get:
    LHS = \frac{3-\sqrt{5}}{3+2\sqrt{5}}\times \frac{3-2\sqrt{5}}{3-2\sqrt{5}}
    {Using (a – b) (a + b) = a2 – b2}
    = \frac{9-3\sqrt{5}-6\sqrt{5}+10}{3^{2}-\left ( 2\sqrt{5} \right )^{2}}
    = \frac{19-9\sqrt{5}}{9-20}
    Now RHS = a\sqrt{5}-\frac{19}{11}
    \Rightarrow \frac{9\sqrt{5}}{11}-\frac{19}{11}= a\sqrt{5}-\frac{19}{11}
    Comparing both , we get
    \Rightarrow a= \frac{9}{11}
    Hence a= \frac{9}{11}is the correct answer
    (iii) Answer:b = -\frac{5 }{6}
    Solution:
    Given:
    \frac{\sqrt{2}+\sqrt{3}}{3 \sqrt{2}-2 \sqrt{3}}=2-b \sqrt{6}
    LHS = \frac{\sqrt{2}+\sqrt{3}}{3 \sqrt{2}-2 \sqrt{3}}
    Rationalize
    = \frac{\sqrt{2}+\sqrt{3}}{3 \sqrt{2}-2 \sqrt{3}} \times \frac{3 \sqrt{2}+2 \sqrt{3}}{3 \sqrt{2}+2 \sqrt{3}}
    =\frac{\sqrt{2}(3 \sqrt{2}+2 \sqrt{3})+\sqrt{3}(3 \sqrt{2}+2 \sqrt{3})}{(3 \sqrt{2})^{2}-(2 \sqrt{3})^{2}}
    = \frac{6+2 \sqrt{6}+3 \sqrt{6}+6}{18-12}
    = 2+\frac{5 \sqrt{6}}{6}
    2+\frac{5 \sqrt{6}}{6}=2-b \sqrt{6}
    b = -\frac{5 }{6}

    (iv) Answer. a = 0, b = 1
    Solution. Given,
    \frac{7+\sqrt{5}}{7-\sqrt{5}}-\frac{7-\sqrt{5}}{7+\sqrt{5}}= a+\frac{7}{11}\sqrt{5b}
    LHS = \frac{7+\sqrt{5}}{7-\sqrt{5}}-\frac{7-\sqrt{5}}{7+\sqrt{5}}
    =\frac{\left ( 7+\sqrt{5} \right )\times\left ( 7+\sqrt{5} \right )-\left ( 7-\sqrt{5} \right ) \times \left ( 7-\sqrt{5} \right )}{\left (7 -\sqrt{5} \right )\left (7 +\sqrt{5} \right )}
    Using (a – b) (a + b) = a2 – b2
    (a + b)2 = a2 + b2 + 2ab
    (a - b)2 = a2 + b2 - 2ab
    = \frac{\left ( 7^{2} +\sqrt{5}^{2}+2\cdot 7\cdot \sqrt{5}\right )-\left ( 7^{2} +\sqrt{5}^{2}-2\cdot 7\cdot \sqrt{5} \right )}{7^{2}-\sqrt{5}^{2}}
    = \frac{\left ( 49+5+14\sqrt{5} \right )-\left ( 49+5-14\sqrt{5} \right )}{49-5}
    = \frac{54+14\sqrt{5}-54+14\sqrt{5}}{44}
    = \frac{28\sqrt{5}}{44}
    RHS = a+\frac{7}{11}\sqrt{5b}
    Now LHS = RHS
    \Rightarrow \frac{28\sqrt{5}}{44}= a+\frac{7}{11}\sqrt{5b}
    \Rightarrow 0+\left ( \frac{4}{4} \right )\frac{7}{11}\sqrt{5}= a+\frac{7}{11}\sqrt{5b}
    \Rightarrow a = 0, b = 1
    Hence the answer is a = 0, b = 1

    Question:12

    If a = 2 + \sqrt{3} then find the value of a-\frac{1}{a}

    Answer:

    Answer. 2\sqrt{3}
    Solution. Given that a = 2\sqrt{3}
    \therefore We have \frac{1}{a}= \frac{1}{2+\sqrt{3}}
    Rationalising,
    \Rightarrow \frac{1}{a}= \frac{1}{2+\sqrt{3}}\times \frac{2-\sqrt{3}}{2-\sqrt{3}}
    Using (a – b) (a + b) = a2 – b2
    \Rightarrow \frac{1}{a}= \frac{2-\sqrt{3}}{2^{2}-\sqrt{3}^{2}}= \frac{2-\sqrt{3}}{4-3}
    \Rightarrow \frac{1}{a}=2-\sqrt{3}
    Now, a- \frac{1}{a}=2+\sqrt{3}-\left ( 2-\sqrt{3} \right )
    \Rightarrow a- \frac{1}{a}=2\sqrt{3}
    Hence the answer is 2\sqrt{3}

    Question:13

    (i) Rationalize the denominator in each of the following and hence evaluate by taking \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732 and \sqrt{5}= 2\cdot 236, upto three places of decimal : \frac{4}{\sqrt{3}}
    (ii) Rationalize the denominator in each of the following and hence evaluate by taking \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732 and \sqrt{5}= 2\cdot 236, upto three places of decimal : \frac{6}{\sqrt{6}}
    (iii) Rationalize the denominator in each of the following and hence evaluate by taking \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732 and \sqrt{5}= 2\cdot 236, upto three places of decimal : \frac{\sqrt{10}-\sqrt{5}}{\sqrt{2}}
    (iv) Rationalize the denominator in each of the following and hence evaluate by taking \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732 and \sqrt{5}= 2\cdot 236, upto three places of decimal : \frac{2}{2+\sqrt{2}}
    (v) Rationalize the denominator in each of the following and hence evaluate by taking \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732 and \sqrt{5}= 2\cdot 236, upto three places of decimal : \frac{1}{\sqrt{3}+\sqrt{2}}

    Answer:

    (i) Answer. 2.3093
    Solution. Given: \frac{4}{\sqrt{3}}
    Rationalising,
    \frac{4}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}= \frac{4\sqrt{3}}{3}
    (Given that \sqrt{3}= 1.732)
    = \frac{4\times 1\cdot 732}{3}
    = 2.3093
    Hence the answer is 2.3093

    (ii) Answer. 2.449
    Solution. Given: \frac{6}{\sqrt{6}}
    Rationalising,
    \frac{6}{\sqrt{6}}\times \frac{\sqrt{6}}{\sqrt{6}}= \frac{6\sqrt{6}}{6}
    = \frac{6\times \sqrt{2}\sqrt{3}}{6}
    Putting the given values,
    \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732
    We get :
    = \sqrt{2}\cdot \sqrt{3}
    = 1\cdot 414\times 1\cdot 732= 2\cdot 449
    Hence the answer is 2.449

    (iii) Answer. 0.462852
    Solution. Given that \frac{\sqrt{10}-\sqrt{5}}{2}
    This can be written as
    \frac{\sqrt{2}\times \sqrt{5}-\sqrt{5}}{2}
    Now putting the given values,
    \sqrt{2}= 1\cdot 414,\sqrt{5}= 2\cdot 236
    We get :
    \Rightarrow \frac{1\cdot 414\times 2\cdot 236-2\cdot 236}{2}
    = 0.462852
    Hence the answer is 0.462852
    (iv) Answer. 0.414
    Solution. Given: \frac{\sqrt{2}}{2+\sqrt{2}}
    Rationalising,
    \frac{\sqrt{2}}{2+\sqrt{2}}\times \frac{2-\sqrt{2}}{2-\sqrt{2}}
    Using (a – b) (a + b) = a2 – b2
    = \frac{\sqrt{2}\left ( 2-\sqrt{2} \right )}{2^{2}-\sqrt{2}^{2}}
    = \frac{2\sqrt{2}-2}{4-2}
    = \frac{2\left ( \sqrt{2}-1 \right )}{2}
    = \sqrt{2}-1
    Putting the given value of \sqrt{2}= 1\cdot 414
    We get
    = 1.414 – 1
    = 0.414
    Hence the answer is 0.414

    (v) Answer. 0.318
    Solution. Given that \frac{1}{\sqrt{3}+\sqrt{2}}
    Rationalising,
    \frac{1}{\sqrt{3}+\sqrt{2}}\times \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}
    Using (a – b) (a + b) = a2 – b2
    = \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}^{2}-\sqrt{2}^{2}}
    = \frac{\sqrt{3}-\sqrt{2}}{3-2}
    = \sqrt{3}-\sqrt{2}
    Putting the given values, \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732
    We get,
    = 1.732 – 1.414
    = 0.318
    Hence the answer is 0.318

    Question:14

    (i) Simplify :- (13 + 23 + 33)1/2
    (ii)     Simplify :- \left ( \frac{3}{5} \right )^{4}\left ( \frac{8}{5} \right )^{-12}\left ( \frac{32}{5} \right )^{6}
    (iii) Simplify :- \left ( \frac{1}{27} \right )^{-\frac{2}{3}}
    (iv) Simplify :- \left [ \left \{ \left ( 625 \right )^{-\frac{1}{2}} \right \}^{-\frac{1}{4}} \right ]^{2}
    (v) Simplify :- \frac{9^{\frac{1}{3}}\times 27^{\frac{1}{2}}}{3^{\frac{1}{6}}\times 9^{-\frac{2}{3}}}
    (vi) Simplify :-64^{-\frac{1}{3}}\left ( 64^{\frac{1}{3}}-64^{\frac{2}{3}} \right )
    (vii) Simplify :- \frac{8^{\frac{1}{3}}\times 16^{\frac{1}{3}}}{32^{-\frac{1}{3}}}
    Answer:

    (i) Answer. 6
    Solution. (13 + 23 + 33)1/2
    We know that
    13 = 1.1.1 = 1
    23 = 2.2.2 = 8
    33 = 3.3.3 = 27
    Putting these values we get
    (13 + 23 + 33)1/2= \sqrt{1+8+27}
    =\sqrt{36}= 6
    Hence the answer is 6

    (ii) Answer.\frac{2025}{64}
    Solution.\left ( \frac{3}{5} \right )^{4}\left ( \frac{8}{5} \right )^{-12}\left ( \frac{32}{5} \right )^{6}
    We know that
    8 = 2.2.2 = 23
    32 = 2.2.2.2.2 = 25
    \left ( \frac{3}{5} \right )^{4}\left ( \frac{8}{5} \right )^{-12}\left ( \frac{32}{5} \right )^{6}= \left ( \frac{3}{5} \right )^{4}\left ( \frac{2^{3}}{5} \right )^{-12}\left ( \frac{2^{5}}{5} \right )^{6}
    = \frac{3^{4}\left ( 2^{3} \right )^{-12}\left ( 2^{5} \right )^{6}}{5^{4}5^{-12}5^{6}} \because \left ( \frac{a}{b} \right )^{m}= \frac{a^{m}}{b^{m}}
    = \frac{3^{4}2^{-36}2^{30}}{5^{4}5^{-12}5^{6}} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = \frac{3^{4}\times 2^{-36+30}}{5^{4-12+6}} \because \left ( a \right )^{m}\left ( a \right )^{n}= \left ( a \right )^{m+n}
    = \frac{3^{4}\times 2^{-6}}{5^{-2}}
    = \frac{3^{4}\times 5^{2}}{2^{6}} \because \left ( a \right )^{-m}= \left ( \frac{1}{a} \right )^{m}
    = \frac{81\times 25}{64}
    = \frac{2025}{64}
    Hence the answer is \frac{2025}{64}

    (iii) Answer. 9
    Solution. Given \left ( \frac{1}{27} \right )^{-\frac{2}{3}}
    We know that
    27 = 3.3.3 = 33
    \left ( \frac{1}{27} \right )^{-\frac{2}{3}}= \left ( \frac{1}{3^{3}} \right )^{-\frac{2}{3}}
    = \left ( 3^{3} \right )^{\frac{2}{3}} \because \left ( a \right )^{-m}= \left ( \frac{1}{a} \right )^{m}
    = \left ( 3 \right )^{3\times \frac{2}{3}} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = 32 = 9
    Hence the answer is 9

    (iv) Answer. 5
    Solution. Given \left [ \left \{ \left ( 625 \right )^{-\frac{1}{2}} \right \}^{-\frac{1}{4}} \right ]^{2}
    We know that
    625= \left ( 25 \right )\left ( 25 \right )= 5\cdot 5\cdot 5\cdot 5= 5^{4}
    \left [ \left \{ \left ( 625 \right )^{-\frac{1}{2}} \right \}^{-\frac{1}{4}} \right ]^{2}= \left [ \left \{ \left ( \left ( 5 \right )^{4} \right )^{-\frac{1}{2}} \right \} ^{-\frac{1}{4}}\right ]^{2}
    = 5^{4\times \frac{-1}{2}\times \frac{-1}{4}\times 2} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = 51 = 5
    Hence the answer is 5

    (v) Answer.\sqrt[3]{\frac{1}{3}}
    Solution. We have \frac{9^{\frac{1}{3}}\times 27^{\frac{1}{2}}}{3^{\frac{1}{6}}\times 9^{-\frac{2}{3}}}
    Now we know that
    9 = 3.3 = 32
    27 = 3.3.3 = 33
    \frac{9^{\frac{1}{3}}\times 27^{\frac{1}{2}}}{3^{\frac{1}{6}}\times 9^{-\frac{2}{3}}}= \frac{\left ( 3^{2} \right )^{\frac{1}{3}}\times \left ( 3^{3} \right )^{\frac{1}{2}}}{\left ( 3 \right )^{\frac{1}{6}}\times \left ( 3^{2} \right )^{\tfrac{-2}{3}}}
    = \frac{\left ( 3\right )^{2\times \frac{1}{3}}\times \left ( 3 \right )^{3\times \frac{-1}{2}}}{\left ( 3 \right )^{\frac{1}{6}}\times \left ( 3 \right )^{\tfrac{-2}{3}}} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = \frac{\left ( 3 \right )^{\frac{2}{3}-\frac{3}{2}}}{\left ( 3 \right )^{\frac{1}{6}-\frac{2}{3}}} \because \left ( a \right )^{m}\left ( a \right )^{n}= \left ( a \right )^{m+n}
    = \frac{3^{\frac{4-9}{6}}}{3^{\frac{1-4}{6}}}
    =\frac{3^{-\frac{5}{6}}}{3^{-\frac{3}{6}}}
    = 3^{\frac{-5}{6}-\left ( \frac{-3}{6} \right )} \because \frac{\left ( a \right )^{m}}{\left ( a \right )^{n}}= \left ( a \right )^{m-n}
    = 3^{-\frac{2}{6}}
    = \left ( \frac{1}{3} \right )^{\frac{1}{3}} \because \left ( a \right )^{-m}= \left ( \frac{1}{a} \right )^{m}
    = \sqrt[3]{\frac{1}{3}}
    Hence the answer is \sqrt[3]{\frac{1}{3}}

    (vi) Answer. – 3
    Solution. We have ,64^{-\frac{1}{3}}\left ( 64^{\frac{1}{3}}-64^{\frac{2}{3}} \right )
    We know that 64 =4.4.4=43
    = \left ( 4^{3} \right )^{\frac{-1}{3}}\left \{ \left ( \left ( 4^{3} \right ) ^{\frac{1}{3}}-\left ( 4^{3} \right ) ^{\frac{2}{3}}\right )\right \}
    = \left ( 4 \right )^{3\times \frac{-1}{3}}\left \{ \left ( \left ( 4 \right )^{3\times \frac{1}{3}}-\left ( 4 \right )^{3\times \frac{2}{3}} \right ) \right \} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = 4^{-1}\left ( 4-4^{2} \right )
    = \frac{1}{4}\left ( 4-16 \right ) \because \left ( a \right )^{-m}= \left ( \frac{1}{a} \right )^{m}
    = \frac{1}{4}\left ( -12 \right )
    = – 3
    Hence the answer is – 3

    (vii) Answer. 16
    Solution.     Given ,\frac{8^{\frac{1}{3}}\times 16^{\frac{1}{3}}}{32^{-\frac{1}{3}}}
    We know that
    8 = 2.2.2 = 23
    16 = 2.2.2.2 = 24
    32 = 2.2.2.2.2 = 25
    \frac{8^{\frac{1}{3}}\times 16^{\frac{1}{3}}}{32^{-\frac{1}{3}}}= \frac{\left ( 2^{3} \right )^{\frac{1}{3}}\times\left ( 2^{4} \right )^{\frac{1}{3}}}{\left ( 2^{5} \right )^{-\frac{1}{3}}}
    = \frac{2^{3\times\frac{1}{3}}\times2^{4\times\frac{1}{3}}}{2^{5\times\frac{-1}{3}}} \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = 2^{1+\frac{4}{3}+\frac{5}{3}} \because \left ( a \right )^{m}\left ( a \right )^{n}= \left ( a \right )^{m+n} and
    \because \frac{\left ( a \right )^{m}}{\left ( a \right )^{n}}= \left ( a \right )^{m-n}
    = 2^{\frac{3+4+5}{3}}= 2^{\frac{12}{3}}
    = 2^{4}= 16
    Hence the answer is 16.

    NCERT Exemplar Class 9 Maths Solutions Chapter-1: Exercise-1.4

    Question:1

    Express 0.6 + 0\cdot \bar{7}+0\cdot \overline{47} in the form \frac{p}{q} where p and q are integers and q\neq 0.
    Answer:

    Answer. \frac{167}{90}
    Solution. Let x = 0.6
    Multiply by 10 on LHS and RHS
    10x = 6
    x= \frac{6}{10}
    x= \frac{3}{5}
    So, the \frac{p}{q} from of 0.6 = \frac{3}{5}
    Let y = 0\cdot \bar{7}
    Multiply by 10 on LHS and RHS
    10y = 7.7777 …….
    10y – y = 7\cdot \bar{7}-0\cdot \bar{7}
    = 7.77777 ….. – 0.77777 ……
    9y = 7
    y= \frac{7}{9}
    So the \frac{p}{q} from of 0.7777 = \frac{7}{9}
    Let z = 0.47777…
    Multiply by 10 on both side
    10z = 4.7777 ….
    10z – z = 4\cdot \bar{7}-0\cdot4\bar{7}
    9z = 4.3
    z\approx \frac{4\cdot 3}{9}
    z= \frac{43}{90}
    So the \frac{p}{q}from of 0.4777 …. = \frac{43}{90}
    Therefore, \frac{p}{q} form of 0.6 + 0\cdot \bar{7}+0\cdot4\bar{7} is,
    x+y+z= \frac{3}{5}+\frac{7}{9}+\frac{43}{90}
    = \frac{\left ( 54+70+43 \right )}{90}
    = \frac{167}{90}
    Hence the answer is \frac{167}{90}

    Question:2

    Simplify :- \frac{7\sqrt{3}}{\sqrt{10}+\sqrt{3}}-\frac{2\sqrt{5}}{\sqrt{6}+\sqrt{5}}-\frac{3\sqrt{2}}{\sqrt{15}+3\sqrt{2}}

    Answer:

    Answer. 1
    Solution.     \frac{7\sqrt{3}}{\sqrt{10}+\sqrt{3}}-\frac{2\sqrt{5}}{\sqrt{6}+\sqrt{5}}-\frac{3\sqrt{2}}{\sqrt{15}+3\sqrt{2}}
    Rationalise the denominators:
    \Rightarrow \left ( \frac{7\sqrt{3}}{\sqrt{10}+\sqrt{3}}\times \frac{\sqrt{10}-\sqrt{3}}{\sqrt{10}-\sqrt{3}} \right )-\left ( \frac{2\sqrt{5}}{\sqrt{6}+\sqrt{3}} \times \frac{\sqrt{6}-\sqrt{5}}{\sqrt{6}-\sqrt{5}}\right )-\left ( \frac{3\sqrt{2}}{\sqrt{15}+3\sqrt{2} } \times\frac{\sqrt{15}-3\sqrt{2}}{\sqrt{15}-3\sqrt{2}}\right )
    \Rightarrow \frac{7\sqrt{3}\left ( \sqrt{10} -\sqrt{3}\right )}{10-3}-\frac{2\sqrt{5}\left ( \sqrt{6}-\sqrt{5} \right )}{6-5}-\frac{3\sqrt{2}\left ( \sqrt{15}-3\sqrt{2} \right )}{15-8}
    \left [ \because a^{2}-b^{2} = \left ( a+b \right )\left ( a-b \right )\right ]
    \Rightarrow \frac{7\sqrt{3}\left ( \sqrt{10} -\sqrt{3}\right )}{7}-\frac{2\sqrt{5}\left ( \sqrt{6}-\sqrt{5} \right )}{1}-\frac{3\sqrt{2}\left ( \sqrt{15}-3\sqrt{2} \right )}{3}
    \Rightarrow \frac{7\sqrt{30}-21}{7}-\frac{2\sqrt{30}-10}{1}+\frac{3\sqrt{30}-18}{3}
    \Rightarrow \frac{21\sqrt{30}-63-42\sqrt{30}+210+21\sqrt{30}-126}{21}
    \Rightarrow \frac{21}{21}= 1
    Hence the answer is 1.

    Question:3

    If \sqrt{2}= 1\cdot 414 and \sqrt{3}= 1\cdot 732 then find the value of \frac{4}{3\sqrt{3}-2\sqrt{2}}+\frac{3}{3\sqrt{3}+2\sqrt{2}}

    Answer:

    Answer. 2.0632
    Solution. Given that :
    \sqrt{2}= 1\cdot 414,\sqrt{3}= 1\cdot 732
    \frac{4}{3\sqrt{3}-2\sqrt{2}}+\frac{3}{3\sqrt{3}+2\sqrt{2}}
    = \frac{4\left ( 3\sqrt{3}+2\sqrt{2} \right )}{\left ( 3\sqrt{3}-2\sqrt{2} \right )\left ( 3\sqrt{3}+2\sqrt{2} \right )}+\frac{3\left ( 3\sqrt{3}-2\sqrt{2} \right )}{\left ( 3\sqrt{3}+2\sqrt{2} \right )\left (3\sqrt{3}-2\sqrt{2} \right )}
    = \frac{4\left ( 3\sqrt{3}+2\sqrt{2} \right )+3\left ( 3\sqrt{3}-2\sqrt{2} \right )}{\left ( 3\sqrt{3}-2\sqrt{2} \right )\left ( 3\sqrt{3}+2\sqrt{2} \right )}
    Using (a – b) (a + b) = a2 – b2
    = \frac{12\sqrt{3}+8\sqrt{2}+9\sqrt{3}-6\sqrt{2}}{\left ( 3\sqrt{3} \right )^{2}-\left ( 2\sqrt{2} \right )^{2}}
    = \frac{21\sqrt{3}+2\sqrt{2}}{27-8}
    = \frac{21\sqrt{3}+2\sqrt{2}}{19}
    Putting the given values,= \frac{21\left ( 1\cdot 732 \right )+2\left ( 1\cdot 414 \right )}{19}
    =\frac{39\cdot 2014}{19}
    = 2.0632
    Hence the answer is 2.0632.

    Question:4

    If a= \frac{3+\sqrt{5}}{2} then find the value of a^{2}= \frac{1}{a^{2}}

    Answer:

    Answer. 7
    Solution.    Given that :- a= \frac{3+\sqrt{5}}{2}
    \therefore \frac{1}{a}= \frac{2}{3+\sqrt{5}}
    On rationalizing the denominator, we get
    \frac{1}{a}= \frac{2\left ( 3-\sqrt{5} \right )}{\left ( 3+\sqrt{5} \right )\left ( 3-\sqrt{5} \right )}
    Using (a – b) (a + b) = a2 – b2
    = \frac{6-2\sqrt{5}}{3^{2}-\sqrt{5}^{2}}
    = \frac{6-2\sqrt{5}}{9-5}
    = \frac{6-2\sqrt{5}}{4}
    = \frac{3-\sqrt{5}}{2}
    Also, \left ( a+\frac{1}{a} \right )^{2}= a^{2}+\frac{1}{a^{2}}+2
    Substituting the values of a and \frac{1}{a}
    We get, \left ( \frac{3+\sqrt{5}}{2}+\frac{3-\sqrt{5}}{2} \right )^{2}= \left ( a^{2}+\frac{1}{a^{2}}+2 \right )
    \therefore a^{2}+\frac{1}{a^{2}}+2= \left ( \frac{3+\sqrt{5}+3-\sqrt{5}}{2} \right )^{2}
    = (3)2 = 9
    \therefore a^{2}+\frac{1}{a^{2}}= 9-2= 7
    Hence the correct answer is 7.

    Question:5

    If x= \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} and y= \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}} then find the value of x2 + y2.

    Answer:

    Answer. 98
    Solution.We use the identity \left ( a+b \right )^{2}= a^{2}+b^{2}+2ab
    So, \left ( \sqrt{a}+\sqrt{b} \right )^{2}= a+2\sqrt{ab}+b
    x^{2}+y^{2}= \left ( \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} \right )^{2}+\left ( \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}} \right )^{2}
    = \frac{3+2\sqrt{6}+2}{3-2\sqrt{6}+2}+\frac{3-2\sqrt{6}+2}{3+2\sqrt{6}+2}
    = \frac{5+2\sqrt{6}}{5-2\sqrt{6}}+\frac{5-2\sqrt{6}}{5+2\sqrt{6}}
    = \frac{\left ( 5+2\sqrt{6} \right )^{2}+\left ( 5-2\sqrt{6} \right )^{2}}{\left ( 5-2\sqrt{6} \right ){\left ( 5+2\sqrt{6} \right )}}
    = \frac{\left ( 25+20\sqrt{6}+24 \right )+\left ( 25-20\sqrt{6} +24\right )}{25-24}

    Using (a – b) (a + b) = a2– b2= 98
    Hence the answer is 98.

    Question:6

    Simplify : \left ( 256 \right )^{-\left ( 4^{\frac{-3}{2}} \right )}

    Answer:

    Answer. 248
    Solution. Given, \left ( 256 \right )^{-\left ( 4^{\frac{-3}{2}} \right )}
    We know that,
    256 = 2.2.2.2.2.2.2.2 = 28
    \left ( 256 \right )^{-\left ( 4^{\frac{-3}{2}} \right )} = \left ( 2^{8} \right )^{\left ( -4 \right )\times \left ( -\frac{3}{2} \right )}
    \because \left ( \left ( a \right ) ^{m}\right )^{n}= \left ( a \right )^{mn}
    =\left ( 2 \right )^{8\times \left ( -4 \right )\times \left ( -\frac{3}{2} \right )}
    = 2^{8\times 4\times \frac{3}{2}}= 2^{8\times 2\times 3}= 2^{48}
    Hence the answer is 248

    Question:7

    Find the value of \frac{4}{\left ( 216 \right )^{\frac{-2}{3}}}+\frac{1}{\left ( 256 \right )^{\frac{-3}{4}}}+\frac{2}{\left ( 243 \right )^{\frac{-1}{5}}}.

    Answer:

    Answer. 214
    Solution. We have, \frac{4}{\left ( 216 \right )^{\frac{-2}{3}}}+\frac{1}{\left ( 256 \right )^{\frac{-3}{4}}}+\frac{2}{\left ( 243 \right )^{\frac{-1}{5}}}
    We know that
    216 = 6.6.6 = 63
    256 = 4.4.4.4 = 44
    243 = 3.3.3.3.3 = 35
    So, \frac{4}{\left ( 216 \right )^{\frac{-2}{3}}}+\frac{1}{\left ( 256 \right )^{\frac{-3}{4}}}+\frac{2}{\left ( 243 \right )^{\frac{-1}{5}}}
    = \frac{4}{\left ( 6^{3} \right )^{\frac{-2}{3}}}+\frac{1}{\left ( 4^{4} \right )^{\frac{-3}{4}}}+\frac{2}{\left ( 3 ^{5}\right )^{-\frac{1}{5}}}
    = \frac{4}{\left ( 6 \right )^{3\times \frac{-2}{3}}}+\frac{1}{\left ( 4 \right )^{4\times \frac{-3}{4}}}+\frac{2}{\left ( 3 \right )^{5\times \frac{-1}{5}}}
    \because \left ( \left ( a \right )^{m} \right )^{n}= \left ( a \right )^{mn}
    = \frac{4}{6^{-2}}+\frac{1}{4^{-3}}+\frac{2}{3^{-1}}
    = 4 × 62 + 43 + 2 × 3
    \because \frac{1}{\left ( a \right )^{-n}}= \left ( a \right )^{n}
    = 4 × 36 + 64 + 6
    = 144 + 70
    = 214
    Hence the answer is 214

    NCERT Exemplar Solutions Class 9 Maths Chapter 1 Number System Important Topics:

    Topics covered in NCERT exemplar Class 9 Maths solutions chapter 1 deals with the understanding of:

    ◊ Real Numbers as Rational numbers and Irrational numbers.

    ◊ Problems to find a rational number between two given numbers or to find an irrational number between two given numbers are dealt with here.

    ◊ The concepts of the number line and locating rational number and irrational numbers on the number line are explained.

    ◊ The decimal expressions of real numbers and fractions are explained in categories like terminating or non-terminating as well as recurring or non-recurring.

    ◊ Questions based on operations performed on real numbers and exponents for real numbers are explained appropriately.

    ◊ Laws of exponents for real numbers such as dealing with multiplications of powers and addition of powers of real numbers are explained through NCERT exemplar Class 9 Maths solutions chapter 1.

    ◊ The concept of rationalising the denominator by multiplication of conjugate of an irrational number is explained through NCERT exemplar solutions for Class 9 Maths chapter 1.

    NCERT Class 9 Maths Exemplar Solutions for Other Chapters:

    Features of NCERT Exemplar Class 9 Maths Solutions Chapter 1 Number System:

    These Class 9 Maths NCERT exemplar solutions chapter 1 will help the students to understand the concept and knowledge of the real numbers. Students of Class 9 can use these solutions as reference material for better study and practice sums of real numbers.

    The NCERT exemplar Class 9 Maths solutions chapter 1 Number System will be adequate to solve problems of other reference books such as NCERT Class 9 Maths, RD Sharma Class 9 Maths or RS Aggarwal Class 9 Maths etcetera.

    NCERT exemplar Class 9 Maths solutions chapter 1 pdf download will be made available to resolve the doubts encountered while attempting the exemplar of chapter 1.

    NCERT Class 9 Exemplar Solutions for Other Subjects:

    Check NCERT Solutions for questions given in book

    Also, check NCERT Solution Subject Wise

    Also, check NCERT Notes Subject Wise

    NCERT Notes for Class 9 Science
    NCERT Notes for Class 9 Maths

    Also Check NCERT Books and NCERT Syllabus here

    Frequently Asked Question (FAQs)

    1. What is the weightage of Number System in Class 9 Maths?

    Number system weighs approximately 8-10% (discretional to the paper setters; varies from school to school for Class 9 Maths)  of the total marks of the paper, however, being one on the basic building blocks for Maths of higher Classes (Class 10, Class 11 and Class 12), the student should understand and practice NCERT exemplar Class 9 Maths chapter 1.

    2. Will these problems of exemplar require additional knowledge of real number?

    The NCERT exemplar Class 9 Maths solutions chapter 1 equip the student with a multidimensional approach to the problems and understanding the concept of Number System.

    3. What is the weightage of Real Numbers in JEE Main and JEE Advanced?

    A clear understanding of Real Number can prepare a student in solving the problems based on fundamentals of maths which ranges from 2-5% marks of the whole paper.

    4. Will it be beneficial to refer NCERT exemplar Class 9 Maths solutions for competitive exams?

    NCERT exemplar Class 9 Maths solutions chapter 1 will provide the student multifaceted problems to hone the skills and prepare well for the competitive exams such as JEE Main.

    5. Why π is an irrational number even its value is 22/7?

    Pi is an irrational number because it is a non-terminating non-recurring decimal number. Recently, a tech company employee has broken the Guinness World Record by calculating Pi till 31.4 trillion (1012) decimal places (See it is never-ending…..)

    6. Is the number of rational numbers more than the number of irrational numbers?

    NCERT exemplar Class 9 Maths solutions chapter 1 explains that both the sets of rational and irrational numbers are infinite; hence, it cannot be deduced.

    Also Read

    Articles

    Upcoming School Exams

    All India Sainik Schools Entrance Examination

    Application Date:06 November,2023 - 15 December,2023

    National Institute of Open Schooling 12th Examination

    Application Date:20 November,2023 - 19 December,2023

    National Institute of Open Schooling 10th examination

    Application Date:20 November,2023 - 19 December,2023

    National Means Cum-Merit Scholarship

    Admit Card Date:22 November,2023 - 02 December,2023

    National Level Science Talent Search Examination

    Exam Date:30 November,2023 - 30 November,2023

    View All School Exams
    Get answers from students and experts

    Popular Questions

    A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

    Option 1)

    0.34\; J

    		 Option 2)

    0.16\; J
    Option 3)

    1.00\; J

    		 Option 4)

    0.67\; J
    Read More

    A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

    Option 1)

    2.45×10−3 kg

    		 Option 2)

     6.45×10−3 kg
    Option 3)

     9.89×10−3 kg

    		 Option 4)

    12.89×10−3 kg

     
    Read More

    An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

    Option 1)

    2,000 \; J - 5,000\; J

    		 Option 2)

    200 \, \, J - 500 \, \, J
    Option 3)

    2\times 10^{5}J-3\times 10^{5}J

    		 Option 4)

    20,000 \, \, J - 50,000 \, \, J
    Read More

    A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

    Option 1)

    K/2\,

    		 Option 2)

    \; K\;
    Option 3)

    zero\;

    		 Option 4)

    K/4
    Read More

    In the reaction,

    2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

    Option 1)

    11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

    		 Option 2)

    6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
    Option 3)

    33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

    		 Option 4)

    67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
    Read More

    How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

    Option 1)

    0.02

    		 Option 2)

    3.125 × 10-2
    Option 3)

    1.25 × 10-2

    		 Option 4)

    2.5 × 10-2
    Read More

    If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

    Option 1)

    decrease twice

    		 Option 2)

    increase two fold
    Option 3)

    remain unchanged

    		 Option 4)

    be a function of the molecular mass of the substance.
    Read More

    With increase of temperature, which of these changes?

    Option 1)

    Molality

    		 Option 2)

    Weight fraction of solute
    Option 3)

    Fraction of solute present in water

    		 Option 4)

    Mole fraction.
    Read More

    Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

    Option 1)

    twice that in 60 g carbon

    		 Option 2)

    6.023 × 1022
    Option 3)

    half that in 8 g He

    		 Option 4)

    558.5 × 6.023 × 1023
    Read More

    A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

    Option 1)

    less than 3

    		 Option 2)

    more than 3 but less than 6
    Option 3)

    more than 6 but less than 9

    		 Option 4)

    more than 9
    Read More

    Colleges After 12th

    Popular Course After 12th

    Explore Career Options (By Industry)

    Bio Medical Engineer

    The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary. 

    4 Jobs Available
    Data Administrator

    Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.

    4 Jobs Available
    Cartographer

    How fascinating it is to represent the whole world on just a piece of paper or a sphere. With the help of maps, we are able to represent the real world on a much smaller scale. Individuals who opt for a career as a cartographer are those who make maps. But, cartography is not just limited to maps, it is about a mixture of art, science, and technology. As a cartographer, not only you will create maps but use various geodetic surveys and remote sensing systems to measure, analyse, and create different maps for political, cultural or educational purposes.

    3 Jobs Available
    Operations Manager

    Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.

    3 Jobs Available
    GIS Expert

    GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.

    3 Jobs Available
    Ethical Hacker

    A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.

    3 Jobs Available
    Database Architect

    If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi. 

    3 Jobs Available
    Data Analyst

    The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

    Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

    3 Jobs Available
    Bank Probationary Officer (PO)

    A career as Bank Probationary Officer (PO) is seen as a promising career opportunity and a white-collar career. Each year aspirants take the Bank PO exam. This career provides plenty of career development and opportunities for a successful banking future. If you have more questions about a career as  Bank Probationary Officer (PO), what is probationary officer or how to become a Bank Probationary Officer (PO) then you can read the article and clear all your doubts. 

    3 Jobs Available
    Operations Manager

    Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.

    3 Jobs Available
    Data Analyst

    The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

    Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

    3 Jobs Available
    Finance Executive

    A career as a Finance Executive requires one to be responsible for monitoring an organisation's income, investments and expenses to create and evaluate financial reports. His or her role involves performing audits, invoices, and budget preparations. He or she manages accounting activities, bank reconciliations, and payable and receivable accounts.  

    3 Jobs Available
    Investment Banker

    An Investment Banking career involves the invention and generation of capital for other organizations, governments, and other entities. Individuals who opt for a career as Investment Bankers are the head of a team dedicated to raising capital by issuing bonds. Investment bankers are termed as the experts who have their fingers on the pulse of the current financial and investing climate. Students can pursue various Investment Banker courses, such as Banking and Insurance, and Economics to opt for an Investment Banking career path.

    3 Jobs Available
    Bank Branch Manager

    Bank Branch Managers work in a specific section of banking related to the invention and generation of capital for other organisations, governments, and other entities. Bank Branch Managers work for the organisations and underwrite new debts and equity securities for all type of companies, aid in the sale of securities, as well as help to facilitate mergers and acquisitions, reorganisations, and broker trades for both institutions and private investors.

    3 Jobs Available
    Treasurer

    Treasury analyst career path is often regarded as certified treasury specialist in some business situations, is a finance expert who specifically manages a company or organisation's long-term and short-term financial targets. Treasurer synonym could be a financial officer, which is one of the reputed positions in the corporate world. In a large company, the corporate treasury jobs hold power over the financial decision-making of the total investment and development strategy of the organisation.

    3 Jobs Available
    Product Manager

    A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

    3 Jobs Available
    Transportation Planner

    A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.

    3 Jobs Available
    Construction Manager

    Individuals who opt for a career as construction managers have a senior-level management role offered in construction firms. Responsibilities in the construction management career path are assigning tasks to workers, inspecting their work, and coordinating with other professionals including architects, subcontractors, and building services engineers.

    2 Jobs Available
    Carpenter

    Carpenters are typically construction workers. They stay involved in performing many types of construction activities. It includes cutting, fitting and assembling wood.  Carpenters may help in building constructions, bridges, big ships and boats. Here, in the article, we will discuss carpenter career path, carpenter salary, how to become a carpenter, carpenter job outlook.

    2 Jobs Available
    Welder

    An individual who opts for a career as a welder is a professional tradesman who is skilled in creating a fusion between two metal pieces to join it together with the use of a manual or fully automatic welding machine in their welder career path. It is joined by intense heat and gas released between the metal pieces through the welding machine to permanently fix it. 

    2 Jobs Available
    Environmental Engineer

    Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems. 

    2 Jobs Available
    Naval Architect

    A Naval Architect is a professional who designs, produces and repairs safe and sea-worthy surfaces or underwater structures. A Naval Architect stays involved in creating and designing ships, ferries, submarines and yachts with implementation of various principles such as gravity, ideal hull form, buoyancy and stability. 

    2 Jobs Available
    Welding Engineer

    Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues. 

    2 Jobs Available
    Field Surveyor

    Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials. 

    2 Jobs Available
    Orthotist and Prosthetist

    Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

    6 Jobs Available
    Pathologist

    A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.

    5 Jobs Available
    Veterinary Doctor

    A veterinary doctor is a medical professional with a degree in veterinary science. The veterinary science qualification is the minimum requirement to become a veterinary doctor. There are numerous veterinary science courses offered by various institutes. He or she is employed at zoos to ensure they are provided with good health facilities and medical care to improve their life expectancy.

    5 Jobs Available
    Gynaecologist

    Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth. 

    4 Jobs Available
    Oncologist

    An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.

    3 Jobs Available
    Surgical Technologist

    When it comes to an operation theatre, there are several tasks that are to be carried out before as well as after the operation or surgery has taken place. Such tasks are not possible without surgical tech and surgical tech tools. A single surgeon cannot do it all alone. It’s like for a footballer he needs his team’s support to score a goal the same goes for a surgeon. It is here, when a surgical technologist comes into the picture. It is the job of a surgical technologist to prepare the operation theatre with all the required equipment before the surgery. Not only that, once an operation is done it is the job of the surgical technologist to clean all the equipment. One has to fulfil the minimum requirements of surgical tech qualifications. 

    Also Read: Career as Nurse

    3 Jobs Available
    Critical Care Specialist

    A career as Critical Care Specialist is responsible for providing the best possible prompt medical care to patients. He or she writes progress notes of patients in records. A Critical Care Specialist also liaises with admitting consultants and proceeds with the follow-up treatments. 

    2 Jobs Available
    Ophthalmologist

    Individuals in the ophthalmologist career in India are trained medically to care for all eye problems and conditions. Some optometric physicians further specialize in a particular area of the eye and are known as sub-specialists who are responsible for taking care of each and every aspect of a patient's eye problem. An ophthalmologist's job description includes performing a variety of tasks such as diagnosing the problem, prescribing medicines, performing eye surgery, recommending eyeglasses, or looking after post-surgery treatment. 

    2 Jobs Available
    Actor

    For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs. 

    4 Jobs Available
    Acrobat

    Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.

    3 Jobs Available
    Video Game Designer

    Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages. Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.

    3 Jobs Available
    Talent Agent

    The career as a Talent Agent is filled with responsibilities. A Talent Agent is someone who is involved in the pre-production process of the film. It is a very busy job for a Talent Agent but as and when an individual gains experience and progresses in the career he or she can have people assisting him or her in work. Depending on one’s responsibilities, number of clients and experience he or she may also have to lead a team and work with juniors under him or her in a talent agency. In order to know more about the job of a talent agent continue reading the article.

    If you want to know more about talent agent meaning, how to become a Talent Agent, or Talent Agent job description then continue reading this article.

    3 Jobs Available
    Radio Jockey

    Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.

    A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.

    3 Jobs Available
    Social Media Manager

    A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.

    2 Jobs Available
    Choreographer

    The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.

    2 Jobs Available
    Talent Director

    Individuals who opt for a career as a talent director are professionals who work in the entertainment industry. He or she is responsible for finding out the right talent through auditions for films, theatre productions, or shows. A talented director possesses strong knowledge of computer software used in filmmaking, CGI and animation. A talent acquisition director keeps himself or herself updated on various technical aspects such as lighting, camera angles and shots. 

    2 Jobs Available
    Copy Writer

    In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook. 

    5 Jobs Available
    Editor

    Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.

    3 Jobs Available
    Journalist

    Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.

    3 Jobs Available
    Publisher

    For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.

    3 Jobs Available
    Vlogger

    In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion. Ever since internet cost got reduced the viewership for these types of content has increased on a large scale. Therefore, the career as vlogger has a lot to offer. If you want to know more about the career as vlogger, how to become a vlogger, so on and so forth then continue reading the article. Students can visit Jamia Millia Islamia, Asian College of Journalism, Indian Institute of Mass Communication to pursue journalism degrees.

    3 Jobs Available
    Travel Journalist

    The career of a travel journalist is full of passion, excitement and responsibility. Journalism as a career could be challenging at times, but if you're someone who has been genuinely enthusiastic about all this, then it is the best decision for you. Travel journalism jobs are all about insightful, artfully written, informative narratives designed to cover the travel industry. Travel Journalist is someone who explores, gathers and presents information as a news article.

    2 Jobs Available
    Videographer

    Careers in videography are art that can be defined as a creative and interpretive process that culminates in the authorship of an original work of art rather than a simple recording of a simple event. It would be wrong to portrait it as a subcategory of photography, rather photography is one of the crafts used in videographer jobs in addition to technical skills like organization, management, interpretation, and image-manipulation techniques. Students pursue Visual Media, Film, Television, Digital Video Production to opt for a videographer career path. The visual impacts of a film are driven by the creative decisions taken in videography jobs. Individuals who opt for a career as a videographer are involved in the entire lifecycle of a film and production. 

    2 Jobs Available
    SEO Analyst

    An SEO Analyst is a web professional who is proficient in the implementation of SEO strategies to target more keywords to improve the reach of the content on search engines. He or she provides support to acquire the goals and success of the client’s campaigns. 

    2 Jobs Available
    Product Manager

    A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

    3 Jobs Available
    Quality Controller

    A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product. 

    A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.

    3 Jobs Available
    Production Manager

    Production Manager Job Description: A Production Manager is responsible for ensuring smooth running of manufacturing processes in an efficient manner. He or she plans and organises production schedules. The role of Production Manager involves estimation, negotiation on budget and timescales with the clients and managers. 

    Resource Links for Online MBA 

    3 Jobs Available
    Team Lead

    A Team Leader is a professional responsible for guiding, monitoring and leading the entire group. He or she is responsible for motivating team members by providing a pleasant work environment to them and inspiring positive communication. A Team Leader contributes to the achievement of the organisation’s goals. He or she improves the confidence, product knowledge and communication skills of the team members and empowers them.

    2 Jobs Available
    Quality Systems Manager

    A Quality Systems Manager is a professional responsible for developing strategies, processes, policies, standards and systems concerning the company as well as operations of its supply chain. It includes auditing to ensure compliance. It could also be carried out by a third party. 

    2 Jobs Available
    Merchandiser

    A career as a merchandiser requires one to promote specific products and services of one or different brands, to increase the in-house sales of the store. Merchandising job focuses on enticing the customers to enter the store and hence increasing their chances of buying a product. Although the buyer is the one who selects the lines, it all depends on the merchandiser on how much money a buyer will spend, how many lines will be purchased, and what will be the quantity of those lines. In a career as merchandiser, one is required to closely work with the display staff in order to decide in what way a product would be displayed so that sales can be maximised. In small brands or local retail stores, a merchandiser is responsible for both merchandising and buying. 

    2 Jobs Available
    Procurement Manager

    The procurement Manager is also known as  Purchasing Manager. The role of the Procurement Manager is to source products and services for a company. A Procurement Manager is involved in developing a purchasing strategy, including the company's budget and the supplies as well as the vendors who can provide goods and services to the company. His or her ultimate goal is to bring the right products or services at the right time with cost-effectiveness. 

    2 Jobs Available
    Production Planner

    Individuals who opt for a career as a production planner are professionals who are responsible for ensuring goods manufactured by the employing company are cost-effective and meets quality specifications including ensuring the availability of ready to distribute stock in a timely fashion manner. 

    2 Jobs Available
    ITSM Manager

    ITSM Manager is a professional responsible for heading the ITSM (Information Technology Service Management) or (Information Technology Infrastructure Library) processes. He or she ensures that operation management provides appropriate resource levels for problem resolutions. The ITSM Manager oversees the level of prioritisation for the problems, critical incidents, planned as well as proactive tasks. 

    3 Jobs Available
    Information Security Manager

    Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack 

    3 Jobs Available
    Computer Programmer

    Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.

    3 Jobs Available
    Product Manager

    A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

    3 Jobs Available
    IT Consultant

    An IT Consultant is a professional who is also known as a technology consultant. He or she is required to provide consultation to industrial and commercial clients to resolve business and IT problems and acquire optimum growth. An IT consultant can find work by signing up with an IT consultancy firm, or he or she can work on their own as independent contractors and select the projects he or she wants to work on.

    2 Jobs Available
    Data Architect

    A Data Architect role involves formulating the organisational data strategy. It involves data quality, flow of data within the organisation and security of data. The vision of Data Architect provides support to convert business requirements into technical requirements. 

    2 Jobs Available
    Security Engineer

    The Security Engineer is responsible for overseeing and controlling the various aspects of a company's computer security. Individuals in the security engineer jobs include developing and implementing policies and procedures to protect the data and information of the organisation. In this article, we will discuss the security engineer job description, security engineer skills, security engineer course, and security engineer career path.

    2 Jobs Available
    UX Architect

    A UX Architect is someone who influences the design processes and its outcomes. He or she possesses a solid understanding of user research, information architecture, interaction design and content strategy. 

     

    2 Jobs Available

    Applications for Admissions are open.

    NEET 2024 Most scoring concepts
    NEET 2024 Most scoring concepts
    Apply

    Just Study 32% of the NEET syllabus and Score upto 100% marks

    ETS ® TOEFL ®
    ETS ® TOEFL ®
    Apply

    Thinking of Studying Abroad? Think the TOEFL® test & make your dreams come true

    JEE Main high scoring chapters and topics
    JEE Main high scoring chapters and topics
    Apply

    As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

    NEET previous year papers with solutions
    NEET previous year papers with solutions
    Apply

    Solve NEET previous years question papers & check your preparedness

    JEE Main Important Mathematics Formulas
    JEE Main Important Mathematics Formulas
    Apply

    As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

    JEE Main Important Physics formulas
    JEE Main Important Physics formulas
    Apply

    As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

    View All Application Forms
    News and Notifications
    37,484 chairs, 6,246 desks ordered for 800 schools of MCD: Official
    22/09/2023, 02:01:05
    CBI books Kendriya Vidyalaya principal for admitting 193 students on fake certificates
    21/09/2023, 17:04:41
    Aadhaar card not mandatory for EWS admission in private schools: Delhi High Court
    21/09/2023, 11:34:59
    25 Assam schools have 0 students; those lacking ‘sustainable' enrolment will be merged, says Ranoj Pegu
    21/09/2023, 11:15:37
    Tamil Nadu Rains: Schools closed in Vellore for Class 1 to 5 due to heavy rainfall
    21/09/2023, 05:22:28
    MCD to open 5 new schools soon, start work on 5 more by December: Officials
    20/09/2023, 17:20:17
    Odisha primary school teachers to hold demonstration outside assembly on September 26
    20/09/2023, 16:17:14

    Everything about Education

    Latest updates, Exclusive Content, Webinars and more.

    Subscribe to Premium
    Back to top