NCERT Solutions for Class 9 Maths Chapter 11 Surface Area and Volumes
Suppose you want to make custom-made conical hats for everyone at your birthday party. Additionally, consider decorating the room with handmade colored balls featuring designs for a more visually appealing look. Now, you need to calculate the amount of materials needed to fulfil these criteria without wastage. For these purposes, one has to know about the Surface Areas and Volumes of a cone and a sphere. Surface Area refers to the total area that the surface of a 3D object covers, while volume measures how much space it occupies. The primary benefit of NCERT Solutions for Class 9 is that they provide clear explanations, making learning simpler and more effective.
This Story also Contains
- Surface Areas and Volumes Class 9 Questions and Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
- Surface Areas and Volumes Class 9 NCERT Solutions: Exercise-wise
- Class 9 Maths NCERT Chapter 11: Extra Question
- Surface Areas and Volumes Class 9 Chapter 11: Topics
- NCERT Surface Areas and Volumes Class 9 Solutions - Important Formulae
- Approach to Solve Questions of Surface Areas and Volumes Class 9
- NCERT Solutions for Class 9 Mathematics: Chapter-wise
Students can find real-life applications of this chapter in many fields, including designing, packaging, decorating, engineering, and event planning. These Surface Areas and Volumes NCERT Solutions for Class 9 Maths are not only important for class 9 board exams but also for higher-class exams and almost every competitive exam. These NCERT Solutions are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
Surface Areas and Volumes Class 9 Questions and Answers PDF Free Download
These NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. You can also download the solutions in PDF format.
NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
|
Class 9 Maths Chapter 11 Question Answers: Exercise: 11.1
Total Questions: 8
Page number: 140-141
|
Answer:
Given,
Base diameter of the cone = $d=10.5\ cm$
Slant height = $l=10\ cm$
We know, Curved surface area of a cone $= \pi r l$
$\therefore$ Required curved surface area of the cone=
$\\ = \frac{22}{7}\times \frac{10.5}{2}\times10 \\ \\ = 165\ cm^2$
Answer:
Given,
Base diameter of the cone = $d=24\ m$
Slant height = $l=21\ cm$
We know, Total surface area of a cone = Curved surface area + Base area
$= \pi r l + \pi r^2 = \pi r (l + r)$
$\therefore$ Required total surface area of the cone=
$\\ = \frac{22}{7}\times\frac{24}{2}\times(21+12) \\ \\ =\frac{22}{7}\times\frac{24}{2}\times33 \\ = 1244.57 \ m^2$
Question 3: (i) Curved surface area of a cone is $\small 308\hspace{1mm}cm^2$, and its slant height is 14 cm. Find the radius of the base.
Answer:
Given,
The curved surface area of a cone = $\small 308\hspace{1mm}cm^2$
Slant height $= l = 14\ cm$
Let the radius of the cone be $r\ cm$
We know, the curved surface area of a cone = $\pi rl$
$\therefore$ $\\ \pi rl = 308 \\ \\ \Rightarrow \frac{22}{7}\times r\times14 = 308 \\ \Rightarrow r = \frac{308}{44} = 7$
Therefore, the radius of the cone is $7\ cm$
Answer:
Given,
The curved surface area of a cone = $\small 308\hspace{1mm}cm^2$
Slant height $= l = 14\ cm$
The radius of the cone is $r =$ $7\ cm$
(ii) We know the total surface area of a cone = the Curved surface area + the Base area
$= \pi r l + \pi r^2$
$\\ = 308+\frac{22}{7}\times 7^2 $
$= 308+154 $
$= 462\ cm^2$
Therefore, the total surface area of the cone is $462\ cm^2$
Question 4: (i) A conical tent is 10 m high, and the radius of its base is 24 m. Find the slant height of the tent.
Answer:
Given,
Base radius of the conical tent = $r=24\ m$
Height of the conical tent = $h=10\ m$
$\therefore$ Slant height, $l=\sqrt{h^2+r^2}$
$\\ =\sqrt{10^2+24^2}$
$ = \sqrt{676}$
$= 26\ m$
Therefore, the slant height of the conical tent is $26\ m$
Answer:
Given,
Base radius of the conical tent = $r=24\ m$
Height of the conical tent = $h=10\ m$
$\therefore$ Slant height = $l=\sqrt{h^2+r^2} = 26\ m$
We know the curved surface area of a cone $= \pi r l$
$\therefore$ Curved surface area of the tent
$\\ = \frac{22}{7}\times24\times26$
$=\frac{13728}{7}\ m^2$
Cost of $1\ m^2$ of canvas = $Rs.\ 70$
$\therefore$ Cost of $\frac{13728}{7}\ m^2$ of canvas
$=Rs.\ (\frac{13728}{7}\times70)$
$ = Rs.\ 137280$
Therefore, the required cost of canvas to make a tent is $Rs.\ 137280$.
Answer:
Given,
Base radius of the conical tent = $r =6\ m$
Height of the tent = $h =8\ m$
We know,
Curved surface area of a cone = $\pi rl = \pi r\sqrt{h^2 + r^2}$
$\therefore$ Area of tarpaulin required = Curved surface area of the tent
$\\ =3.14\times6\times \sqrt{8^2+ 6^2} $
$= 3.14\times6\times 10 $
$= 188.4\ m^2$
Now, let the length of the tarpaulin sheet be $x\ m$
Since $20\ cm$ is wasted, effective length = $x - 20 cm = (x - 0.2)\ m$
Breadth of tarpaulin = $3\ m$
$\\ \therefore [(x - 0.2) \times 3] = 188.4 $
$ \Rightarrow x - 0.2 = 62.8 $
$ \Rightarrow x = 63\ m$
Therefore, the length of the required tarpaulin sheet will be 63 m.
Answer:
Given, a conical tomb
The base diameter of the cone = $d =14\ m$
Slant height $= l = 25\ m$
We know the curved surface area of a cone $= \pi r l$
$\\ = \frac{22}{7}\times\frac{14}{2}\times25 $
$= 22\times25 $
$ = 550\ m^2$
Now, Cost of whitewashing per $\small 100\hspace{1mm}m^2$ = $\small Rs.\ 210$
$\therefore$ Cost of whitewashing per $\small 550\hspace{1mm}m^2$
= $\small \\ Rs. (\frac{210}{100}\times550 )$
$\small \\ = Rs.\ (21\times55 ) = Rs.\ 1155$
Therefore, the cost of whitewashing its curved surface of the tomb is $\small Rs.\ 1155$.
Answer:
Given a right circular cone cap (which means no base)
Base radius of the cone = $r=7\ cm$
Height $= h = 24\ cm$
$\therefore l = \sqrt{h^2+r^2}$
We know the curved surface area of a right circular cone $= \pi r l$
$\therefore$ The curved surface area of a cap =
$\\ = \frac{22}{7}\times7\times\sqrt{24^2+7^2}$
$ = 22\times\sqrt{625} $
$ = 22\times25$
$ = 550\ cm^2$
$\therefore$ The curved surface area of 10 caps
= $550\times10 = 5500\ cm^2$
Therefore, the area of the sheet required for 10 caps = $5500\ cm^2$
Answer:
Given, hollow cone.
The base diameter of the cone = $d = 40\ cm = 0.4\ m$
Height of the cone = $h = 1\ m$
$\therefore$ Slant height = $l = \sqrt{h^2+r^2}$ $= \sqrt{1^2+0.2^2}$
We know, Curved surface area of a cone = $\pi r l = \pi r\sqrt{h^2+r^2}$
$\therefore$ The curved surface area of 1 cone
$= 3.14\times0.2\times\sqrt{1.04}$
$ = 3.14\times0.2\times1.02$
$= 0.64056\ m^2$
$\therefore$ The curved surface area of 50 cones $= (50\times0.64056)\ m^2$
$= 32.028\ m^2$
Now, the cost of painting $\small 1\ m^2$ area = $\small Rs.\ 12$
$\therefore$ Cost of the painting $32.028\ m^2$ area
$= Rs.\ (32.028\times12)$
$= Rs.\ 384.336$
Therefore, the cost of painting 50 such hollow cones is $Rs.\ 384.34$ (approx).
|
Class 9 Maths Chapter 11 Question Answers: Exercise: 11.2 |
Question 1: (i) Find the surface area of a sphere of radius: $\small 10.5\hspace{1mm}cm$.
Answer:
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area = $4\times\frac{22}{7} \times(10.5)^2$
$\\ =88\times1.5\times10.5 \\ = 1386\ cm^2$
Question 1: (ii) Find the surface area of a sphere of radius: $\small 5.6\hspace{1mm}cm$
Answer:
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area = $4\times\frac{22}{7} \times(5.6)^2$
$\\ =88\times0.8\times5.6 \\ = 394.24\ cm^2$
Question 1: (iii) Find the surface area of a sphere of radius: $\small 14\hspace{1mm}cm$
Answer:
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area
$= 4\times\frac{22}{7} \times(14)^2$
$\\ = 88\times2\times14$
$= 2464 \ cm^2$
Question 2: (i) Find the surface area of a sphere of diameter: 14 cm
Answer:
Given,
The diameter of the sphere = $14\ cm$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area
$=4\times\frac{22}{7} \times\left (\frac{14}{2} \right )^2$
$= 4\times\frac{22}{7} \times\frac{14}{2}\times\frac{14}{2}$
$\\ = 22\times2\times14 \\ = 616\ cm^2$
Question 2: (ii) Find the surface area of a sphere of diameter: 21 cm
Answer:
Given,
The diameter of the sphere = $21\ cm$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area
$=4\times\frac{22}{7} \times\left (\frac{21}{2} \right )^2$
$= 4\times\frac{22}{7} \times\frac{21}{2}\times\frac{21}{2}$
$\\ = 22\times3\times21 \\ = 1386\ cm^2$
Question 2: (iii) Find the surface area of a sphere of diameter: $\small 3.5\hspace{1mm}m$
Answer:
Given,
The diameter of the sphere = $3.5\ m$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ Required surface area
$=4\times\frac{22}{7} \times\left (\frac{3.5}{2} \right )^2$
$= 4\times\frac{22}{7} \times\frac{3.5}{2}\times\frac{3.5}{2}$
$\\ = 22\times0.5\times3.5 \\ = 38.5\ m^2$
Question 3: Find the total surface area of a hemisphere of radius 10 cm. (Use $\small \pi =3.14$ )
Answer:
We know,
The total surface area of a hemisphere = Curved surface area of hemisphere + Area of the circular end
$= 2\pi r^2 + \pi r^2 = 3\pi r^2$
$\therefore$ The required total surface area of the hemisphere
$=3\times3.14\times(10)^2$
$\\ = 942\ cm^2$
Answer:
Given,
$r_1 = 7\ cm$
$r_2 = 14\ cm$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ The ratio of surface areas of the ball in the two cases
= $\frac{Initial}{Final} = \frac{4\pi r_1^2}{4\pi r_2^2}$
$= \frac{r_1^2}{r_2^2}$
$\\ = \left (\frac{7}{14} \right )^2$
$= \left (\frac{1}{2} \right )^2$
$= \frac{1}{4}$
Therefore, the required ratio is $1:4$
Answer:
Given,
The inner radius of the hemispherical bowl = $r = \frac{10.5}{2}\ cm$
We know,
The curved surface area of a hemisphere = $2\pi r^2$
$\therefore$ The surface area of the hemispherical bowl
$=2\times\frac{22}{7}\times\left (\frac{10.5}{2} \right )^2$
$=11\times1.5\times10.5$
$= 173.25 \ cm^2$
Now,
Cost of tin-plating $\small 100\hspace{1mm}cm^2$ = Rs 16
$\therefore$ Cost of tin-plating $\small 33\hspace{1mm}cm^2$
= $\small \\ Rs. \left (\frac{16}{100}\times173.25 \right )$
$\small = Rs. 27.72$
Therefore, the cost of tin-plating it on the inside is $\small Rs. 27.72$
Question 6: Find the radius of a sphere whose surface area is $\small 154\hspace{1mm}cm^2$.
Answer:
Given,
The surface area of the sphere = $\small 154\hspace{1mm}cm^2$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore 4\pi r^2 = 154$
$\\ \Rightarrow 4\times\frac{22}{7}\times r^2 = 154$
$\\ \Rightarrow r^2 = \frac{154\times7}{4\times22} = \frac{7\times7}{4}$
$\\ \Rightarrow r = \frac{7}{2}$
$\\ \Rightarrow r = 3.5\ cm$
Therefore, the radius of the sphere is $3.5\ cm$
Answer:
Let the diameter of the Moon be $d_m$ and the diameter of Earth be $d_e$
We know,
The surface area of a sphere of radius $r$ = $4\pi r^2$
$\therefore$ The ratio of their surface areas = $\frac{\text{Surface area of moon}}{\text{Surface area of Earth}}$
$= \frac{4\pi \left (\frac{d_m}{2} \right )^2}{4\pi \left (\frac{d_e}{2} \right )^2}$
$= \frac{d_m^2}{d_e^2}$
$=\left ( \frac{\frac{1}{4}d_e}{d_e} \right )^2$
$= \frac{1}{16}$
Therefore, the ratio of the surface areas of the moon and earth is $= 1:16$
Answer:
Given,
The inner radius of the bowl = $r_1 = 5\ cm$
The thickness of the bowl = $\small 0.25\hspace{1mm}cm$
$\therefore$ Outer radius of the bowl = (Inner radius + thickness) =
$r_2 = 5+0.25 = 5.25\ cm$
We know the curved surface area of a hemisphere of radius $r$ = $2\pi r^2$
$\therefore$ The outer curved surface area of the bowl = $2\pi r_2^2$
$= 2\times\frac{22}{7}\times (5.25)^2$
$= 2\times\frac{22}{7}\times5.25\times5.25 = 173.25\ cm^2$
Therefore, the outer curved surface area of the bowl is $173.25\ cm^2$.
Question 9: (i) A right circular cylinder just encloses a sphere of radius $\small r$ (see Fig. $\small 13.22$ ). Find the surface area of the sphere,
Answer:
Given,
The radius of the sphere = $r$
$\therefore$ Surface area of the sphere = $4\pi r^2$
Question 9: (ii) A right circular cylinder just encloses a sphere of radius $\small r$ (see Fig. $\small 13.22$ ). Find the curved surface area of the cylinder,
Answer:
Given,
The radius of the sphere = $r$
$\therefore$ The surface area of the sphere = $4\pi r^2$
According to the question, the cylinder encloses the sphere.
Hence, the diameter of the sphere is the diameter of the cylinder.
Also, the height of the cylinder is equal to the diameter of the sphere.
We know the curved surface area of a cylinder
= $2\pi rh$
$= 2\pi r(2r) = 4\pi r^2$
Therefore, the curved surface area of the cylinder is $4\pi r^2$
Question 9: (iii) A right circular cylinder just encloses a sphere of radius $\small r$ (see Fig. $\small 13.22$ ). Find the ratio of the areas obtained in (i) and (ii).
Answer:
The surface area of the sphere = $4\pi r^2$
And, the Surface area of the cylinder = $4\pi r^2$
So, the ratio of the areas = $\frac{4\pi r^2}{4\pi r^2} = 1$
|
Class 9 Maths Chapter 11 Question Answers: Exercise: 11.3 |
Question 1: (i) Find the volume of the right circular cone with radius 6 cm, height 7 cm
Answer:
Given,
Radius = $r =6\ cm$
Height = $h =7\ cm$
We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ Required volume
$=\frac{1}{3}\times\frac{22}{7}\times6^2\times7$
$\\ = 22\times2\times6$
$= 264\ cm^3$
Question 1 (ii) Find the volume of the right circular cone with radius $\small 3.5$ cm, height 12 cm
Answer:
Given,
Radius = $r =3.5\ cm$
Height = $h =12\ cm$
We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ Required volume
$=\frac{1}{3}\times\frac{22}{7}\times3.5^2\times12$
$\\ = 22\times0.5\times3.5\times4 $
$= 11\times14$
$ = 154\ cm^3$
Question 2: (i) Find the capacity in litres of a conical vessel with radius 7 cm, slant height 25 cm
Answer:
Given,
Radius = $r =7\ cm$
Slant height = $l = \sqrt{r^2 + h^2} = 25\ cm$
Height = $h =\sqrt{l^2-r^2}$
$ = \sqrt{25^2-7^2}$
$= \sqrt{(25-7)(25+7)}$
$ = \sqrt{(18)(32)}$
$= 24\ cm$
We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ Volume of the vessel
$=\frac{1}{3}\times\frac{22}{7}\times7^2\times24$
$\\ = 22\times7\times8$
$= 154\times8 $
$= 1232\ cm^3$
$\therefore$ Required capacity of the vessel
$= \frac{1232}{1000} = 1.232\ litres$
Question 2: (ii) Find the capacity in litres of a conical vessel with height 12 cm, slant height 13 cm
Answer:
Given,
Height = $h =12\ cm$
Slant height = $l = \sqrt{r^2 + h^2} = 13\ cm$
Radius = $r =\sqrt{l^2-h^2} $
$= \sqrt{13^2-12^2}$
$= \sqrt{(13-12)(13+12)} $
$= \sqrt{(1)(25)}$
$= 5\ cm$
We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ Volume of the vessel
$=\frac{1}{3}\times\frac{22}{7}\times5^2\times12$
$\\ = \frac{22}{7}\times25\times4$
$= \frac{2200}{7}\ cm^3$
$\therefore$ Required capacity of the vessel
$= \frac{2200}{7\times1000} $
$= \frac{11}{35}\ litres$
Answer:
Given,
Height of the cone = $h =15\ cm$
Let the radius of the base of the cone be $r\ cm$
We know,
The volume of a right circular cone
$=\frac{1}{3}\pi r^2 h$
$\therefore$ $\frac{1}{3}\times3.14\times r^2\times15 = 1570$
$\Rightarrow 3.14\times r^2\times5 = 1570$
$ \Rightarrow r^2 = \frac{1570}{15.7} $
$ \Rightarrow r^2 = 100$
$ \Rightarrow r = 10\ cm$
Answer:
Given,
Height of the cone = $h =9\ cm$
Let the radius of the base of the cone be $r\ cm$
We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ $\frac{1}{3}\times\pi\times r^2\times9 = 48\pi$
$\\ \Rightarrow 3r^2 = 48$
$ \Rightarrow r^2 = 16$
$ \Rightarrow r = 4\ cm$
Therefore, the diameter of the right circular cone is $8\ cm$
Question 5: A conical pit of top diameter $\small 3.5$ m is 12 m deep. What is its capacity in kilolitres?
Answer:
Given,
Depth of the conical pit = $h =12\ m$
The top radius of the conical pit = $r = \frac{3.5}{2}\ m$
We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ The volume of the conical pit
$= \frac{1}{3}\times\frac{22}{7}\times \left (\frac{3.5}{2} \right )^2\times12$
$\\ = \frac{1}{3}\times\frac{22}{7}\times \frac{3.5\times 3.5}{4}\times12 $
$= 22\times 0.5\times 3.5 $
$ = 38.5\ m^3$
Now, $1\ m^3 = 1\ kilolitre$
$\therefore$ The capacity of the pit = $38.5\ kilolitre$
Question 6: (i) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$. If the diameter of the base is 28 cm, find the height of the cone
Answer:
Given a right circular cone.
The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$
The volume of the cone = $\small 9856\hspace{1mm}cm^3$
(i) Let the height of the cone be $h\ m$.
We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$
$\therefore$ $\frac{1}{3}\times\frac{22}{7}\times(14)^2\times h = 9856$
$\\ \Rightarrow \frac{1}{3}\times\frac{22}{7}\times14\times14\times h = 9856$
$ \Rightarrow \frac{1}{3}\times22\times2\times14\times h = 9856$
$ \Rightarrow h = \frac{9856\times3}{22\times2\times14} $
$ \Rightarrow h =48\ cm$
Therefore, the height of the cone is $48\ cm$
Question 6: (ii) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$. If the diameter of the base is 28 cm, find the Slant height of the cone
Answer:
Given a right circular cone.
The volume of the cone = $\small 9856\hspace{1mm}cm^3$
The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$
And the height of the cone = $h = 48\ cm$
(ii) We know the slant height, $l = \sqrt{r^2+h^2}$
$ \Rightarrow l = \sqrt{14^2+48^2}$
$ \Rightarrow l = \sqrt{196+2304} = \sqrt{2500} $
$ \Rightarrow l = 50\ cm$
Therefore, the slant height of the cone is $50\ cm$.
Question 6: (iii) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$. If the diameter of the base is 28 cm, find the curved surface area of the cone
Answer:
Given a right circular cone.
The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$
And Slant height of the cone = $l = 50\ cm$
(iii) We know,
The curved surface area of a cone = $\pi r l$
$\therefore$ Required curved surface area
$=\frac{22}{7}\times14\times50$
$\\ = 22\times2\times50$
$= 2200\ cm^2$
Answer:
When a right-angled triangle is revolved about the perpendicular side, a cone is formed whose,
Height of the cone = Length of the axis= $h = 12\ cm$
Base radius of the cone = $r = 5\ cm$
And, Slant height of the cone = $l = 13\ cm$
We know,
The volume of a cone = $\frac{1}{3}\pi r^2 h$
The required volume of the cone formed
$=\frac{1}{3}\times\pi\times5^2\times12$
$\\ = \pi\times25\times4 $
$ = 100\pi\ cm^3$
Therefore, the volume of the solid cone obtained is $100\pi\ cm^3$.
Answer:
When a right-angled triangle is revolved about the perpendicular side, a cone is formed whose,
Height of the cone = Length of the axis= $h = 5\ cm$
Base radius of the cone = $r = 12\ cm$
And, Slant height of the cone = $l = 13\ cm$
We know,
The volume of a cone = $\frac{1}{3}\pi r^2 h$
The required volume of the cone formed
$=\frac{1}{3}\times\frac{22}{7}\times12^2\times5$
$\\ = \pi\times4\times60$
$ = 240\pi\ cm^3$
Now, the Ratio of the volumes of the two solids
$\\ = \frac{100\pi}{240\pi}$
$\\ = \frac{5}{12}$
Therefore, the required ratio is $5:12$.
Answer:
Given,
Height of the conical heap = $h = 3\ m$
Base radius of the cone = $r = \frac{10.5}{2}\ m$
We know,
The volume of a cone = $\frac{1}{3}\pi r^2 h$
The required volume of the cone formed
$=\frac{1}{3}\times\frac{22}{7}\times\left (\frac{10.5}{2} \right )^2\times3$
$\\ = 22\times\frac{1.5\times10.5}{4}$
$ = 86.625\ m^3$
Now,
The slant height of the cone, $l = \sqrt{r^2+h^2}$
$\Rightarrow l = \sqrt{3^2+5.25^2} = \sqrt{9+27.5625} \approx 6.05$
We know the curved surface area of a cone = $\pi r l$
The required area of the canvas to cover the heap
$=\frac{22}{7}\times\frac{10.5}{2}\times6.05$
$= 99.825\ m^2$
|
Class 9 Maths Chapter 11 Question Answers: Exercise: 11.4
Total Questions: 10 Page number: 150 |
Question 1: (i) Find the volume of a sphere whose radius is 7 cm
Answer:
Given,
The radius of the sphere = $r = 7\ cm$
We know, Volume of a sphere = $\frac{4}{3}\pi r^3$
The required volume of the sphere
$=\frac{4}{3}\times\frac{22}{7}\times (7)^3$
$\\ = \frac{4}{3}\times22\times 7\times 7$
$\\ = \frac{4312}{3}$
$\\ = 1437\frac{1}{3}\ cm^3$
Question 1 (ii) Find the volume of a sphere whose radius is $\small 0.63\hspace{1mm}m$
Answer:
Given,
The radius of the sphere = $r = 0.63\ m$
We know, Volume of a sphere = $\frac{4}{3}\pi r^3$
The required volume of the sphere
$=\frac{4}{3}\times\frac{22}{7}\times (0.63)^3$
$\\ = 4\times22\times 0.03\times 0.63\times 0.63$
$\\ = 1.048\ m^3$
$\\ = 1.05\ m^3$ (approx)
Question 2: (i) Find the amount of water displaced by a solid spherical ball of a diameter of 28 cm
Answer:
The solid spherical ball will displace water equal to its volume.
Given,
The radius of the sphere = $r = \frac{28}{2}\ cm = 14\ cm$
We know, Volume of a sphere = $\frac{4}{3}\pi r^3$
$\therefore$ The required volume of the sphere
$=\frac{4}{3}\times\frac{22}{7}\times (14)^3$
$\\ = \frac{4}{3}\times22\times 2\times 14\times 14$
$\\ = \frac{34469}{3} $
$ = 11489\frac{2}{3}\ cm^3$
Therefore, the amount of water displaced will be $11489\frac{2}{3}\ cm^3$.
Question 2: (ii) Find the amount of water displaced by a solid spherical ball of diameter $\small 0.21\hspace{1mm}m$
Answer:
The solid spherical ball will displace water equal to its volume.
Given,
The radius of the sphere = $r = \frac{0.21}{2}\ m$
We know, Volume of a sphere = $\frac{4}{3}\pi r^3$
$\therefore$ The required volume of the sphere
$=\frac{4}{3}\times\frac{22}{7}\times \left(\frac{0.21}{2} \right )^3$
$\\ = 4\times22\times \frac{0.01\times 0.21\times 0.21}{8}$
$\\ = 11\times 0.01\times 0.21\times 0.21$
$\\ =0.004851\ m^3$
Therefore, the amount of water displaced will be $0.004851\ m^3$.
Answer:
Given,
The radius of the metallic sphere = $r = \frac{4.2}{2}\ cm = 2.1\ cm$
We know, Volume of a sphere = $\frac{4}{3}\pi r^3$
$\therefore$ The required volume of the sphere
$=\frac{4}{3}\times\frac{22}{7}\times 2.1^3$
$ = 4\times22\times 0.1\times 2.1\times 2.1$
$ =38.808\ cm^3$
Now, the density of the metal is $\small 8.9\hspace{1mm}g$ per $\small cm^3$, which means,
Mass of $\small 1\ cm^3$ of the metallic sphere = $\small 8.9\hspace{1mm}g$
Mass of $38.808\ cm^3$ of the metallic sphere = $\small (8.9\times38.808)\ g$
$\small \approx 345.39\ g$
Answer:
Given,
Let $d_e$ be the diameter of Earth.
$\therefore$ The diameter of the Moon = $d_m = \frac{1}{4}d_e$
We know the volume of a sphere
$=\frac{4}{3}\pi r^3$
$ =\frac{4}{3}\pi \left (\frac{d}{2} \right )^3$
$ = \frac{1}{6}\pi d^3$
$\therefore$ The ratio of the volumes
$=\frac{\text{Volume of the Earth}}{\text{Volume of the Moon}}$
$= \frac{\frac{1}{6}\pi d_e^3}{\frac{1}{6}\pi d_m^3} $
$= \frac{ d_e^3}{(\frac{d_e}{4})^3} $
$= 64: 1$
Therefore, the required ratio of the volume of the moon to the volume of the earth is $1: 64$.
Question 5: How many litres of milk can a hemispherical bowl of diameter $\small 10.5\hspace{1mm}cm$ hold?
Answer:
The radius of the hemispherical bowl = $r = \frac{10.5}{2}\ cm$
We know, Volume of a hemisphere = $\frac{2}{3}\pi r^3$
The volume of the given hemispherical bowl = $\frac{2}{3}\times\frac{22}{7}\times \left (\frac{10.5}{2} \right )^3$
$= \frac{2}{3\times8}\times22\times1.5\times10.5\times10.5$
$= 303.1875\ cm^3$
The capacity of the hemispherical bowl
$= \frac{303.1875}{1000} \approx 0.303\ litres$ (approx).
Answer:
Given,
Inner radius of the hemispherical tank = $r_1 = 1\ m$
Thickness of the tank = $1\ cm = 0.01\ m$
$\therefore$ Outer radius = Internal radius + thickness = $r_2 = (1+0.01)\ m = 1.01\ m$
We know, Volume of a hemisphere = $\frac{2}{3}\pi r^3$
$\therefore$ Volume of the iron used = Outer volume - Inner volume
$= \frac{2}{3}\pi r_2^3 - \frac{2}{3}\pi r_1^3$
$= \frac{2}{3}\times\frac{22}{7}\times (1.01^3 - 1^3)$
$= \frac{44}{21}\times0.030301$
$= 0.06348\ m^3$ (approx)
Question 7: Find the volume of a sphere whose surface area is $\small 154\hspace{1mm}cm^2$.
Answer:
Given,
The surface area of the sphere = $\small 154\hspace{1mm}cm^2$
We know the surface area of a sphere = $4\pi r^2$
$\therefore 4\pi r^2 = 154$
$\\ \Rightarrow 4\times\frac{22}{7}\times r^2 = 14\times11$
$ \Rightarrow r^2 = \frac{7\times7}{4} $
$ \Rightarrow r = \frac{7}{2} $
$ \Rightarrow r = 3.5\ cm$
$\therefore$ The volume of the sphere
$=\frac{4}{3}\pi r^3$
$= \frac{4}{3}\times\frac{22}{7}\times (3.5)^3$
$= 179\frac{2}{3}\ cm^3$
Answer:
Given,
$\small Rs\hspace{1mm}20$ is the cost of white-washing $1\ m^2$ of the inside area
$\small Rs\hspace{1mm}4989.60$ is the cost of white-washing of:
$\frac{1}{20}\times4989.60\ m^2 = 249.48\ m^2$ of inside area
(i) Therefore, the surface area of the inside of the dome is $249.48\ m^2$
Answer:
Let the radius of the hemisphere be $r\ m$
Inside the surface area of the dome = $249.48\ m^2$
We know the surface area of a hemisphere = $2\pi r^2$
$\\ \therefore 2\pi r^2 = 249.48 $
$ \Rightarrow r^2 = \frac{249.48\times7}{2\times22} $
$ \Rightarrow r = 6.3\ m$
$\therefore$ The volume of the hemisphere
$=\frac{2}{3}\pi r^3$
$= \frac{2}{3}\times\frac{22}{7}\times (6.3)^3$
$= 523.908\ m^3$
Answer:
Given,
The radius of a small sphere = $r$
The radius of the bigger sphere = $r'$
$\therefore$ The volume of each small sphere= $\frac{4}{3}\pi r^3$
And, Volume of the big sphere of radius $r'$ = $\frac{4}{3}\pi r'^3$
According to the question,
$27\times\frac{4}{3}\pi r^3=\frac{4}{3}\pi r'^3$
$\\ \Rightarrow r'^3 = 27\times r^3 $
$ \Rightarrow r' = 3\times r$
$\therefore r' = 3r$
Question 9: (ii) Twenty-seven solid iron spheres, each of radius r and surface area S, are melted to form a sphere with surface area $\small S'$. Find the ratio of S and $\small S'$.
Answer:
Given,
The radius of a small sphere = $r$
The surface area of a small sphere = $S$
The radius of the bigger sphere = $r'$
The surface area of the bigger sphere = $S'$
And, $r' = 3r$
We know the surface area of a sphere = $4\pi r^2$
$\therefore$ The ratio of their surface areas
$=\frac{4\pi r'^2}{4\pi r^2}$
$\\ = \frac{ (3r)^2}{ r^2} \\ = 9$
Therefore, the required ratio is $1:9$.
Answer:
Given,
The radius of the spherical capsule = $r =\frac{3.5}{2}$
$\therefore$ The volume of the capsule = $\frac{4}{3}\pi r^3$
$= \frac{4}{3}\times\frac{22}{7}\times(\frac{3.5}{2})^3$
$= \frac{4}{3}\times22\times\frac{0.5\times3.5\times3.5}{8}$
$= 22.458\ mm^3 \approx 22.46\ mm^3$ (approx)
Therefore, approximately $22.46\ mm^3$ of medicine is needed to fill the capsule.
Surface Areas and Volumes Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Surface Areas and Volumes Class 9 Maths Chapter 11 are provided in the link below.
Class 9 Maths NCERT Chapter 11: Extra Question
Question: A cylindrical water tank has a radius of 3.5 m and a height of 5 m. Find the total surface area of the tank (including top and bottom).
Answer:
Total area of Cylinder = 2πr (r + h)
Given: Radius = 3.5 m and Height = 5 m
So, after putting values, we get;
= $2 \times \frac{22}{7} \times 3.5 \times (3.5 + 5) = 2 \times \frac{22}{7} \times 3.5 \times 8.5$
= $2 \times \frac{22}{7} \times 29.75 = \frac{44 \times 29.75}{7} = \frac{1309}{7}$ = 187 m2
Surface Areas and Volumes Class 9 Chapter 11: Topics
Students will explore the following topics in NCERT Class 9 Maths Chapter 11 Surface Area and Volumes:
- Surface Area of a Right Circular Cone
- Surface Area of a Sphere
- Volume of a Right Circular Cone
- Volume of a Sphere
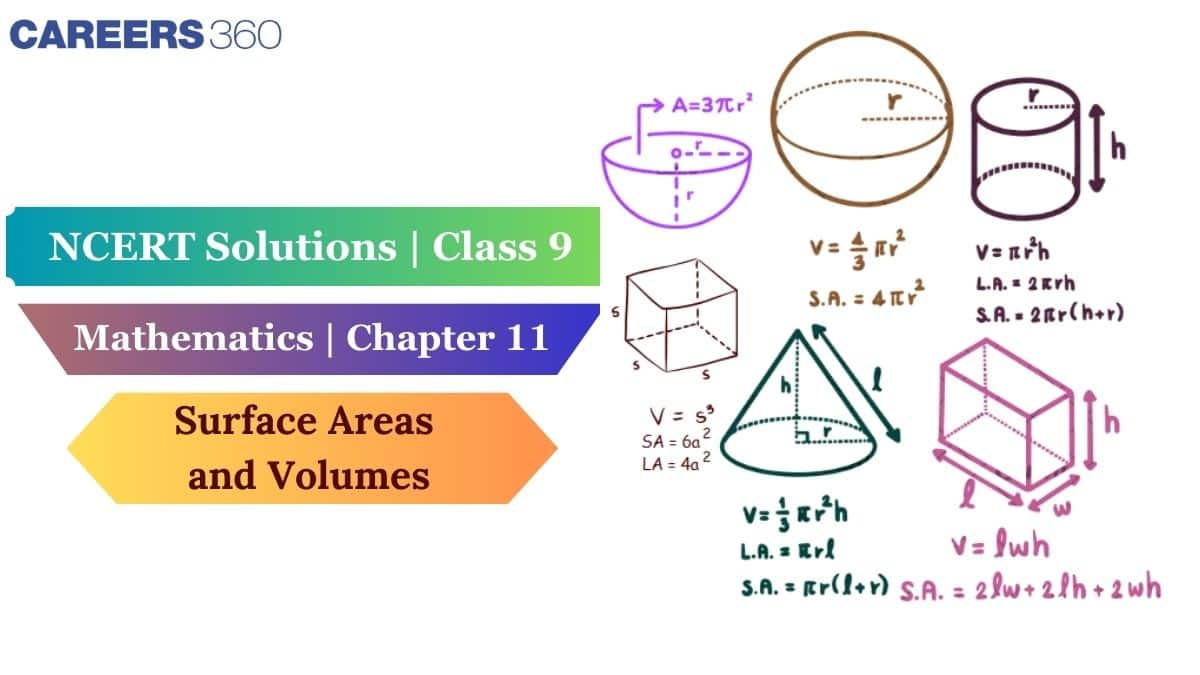
NCERT Surface Areas and Volumes Class 9 Solutions - Important Formulae
Total Surface Area (TSA):
-
Cuboid = 2(l x b) + 2(b x h) + 2(h x l)
-
Cube = 6a2
-
Right Circular Cylinder = 2πr(h + r)
-
Right Circular Cone = πr(l + r)
-
Sphere = 4πr2
-
Hemisphere = 3πr2
Lateral/Curved Surface Area (CSA):
-
Cuboid = 2h(l + b)
-
Cube = 4a2
-
Right Circular Cylinder = 2πrh
-
Right Circular Cone = πrl
Volume:
-
Cuboid = l x b x h
-
Cube = a3
-
Right Circular Cylinder = $πr^2h$
-
Right Circular Cone = $\frac{1}{3}πr^2h$
-
Sphere = $\frac{4}{3}πr^3$
-
Hemisphere = $\frac{2}{3}πr^3$
In these formulas,
$l$ = length
$b$ = breadth
$h$ = height
$r$ = radius
$a$ = side length of the respective geometric figure
Approach to Solve Questions of Surface Areas and Volumes Class 9
Using these approaches, students can tackle the Surface Areas and Volumes Class 9 Chapter 11 Question Answers with greater confidence.
- Memorise standard formulas: Study the surface area and volume equations for cube, cuboid, cylinder, cone, sphere and hemisphere entirely.
- Break complex solids into parts: The calculation process for compound figures requires division into basic parts such as cones and cylinders, followed by separate calculations, which should then be combined.
- Convert units when necessary: All measurements should be uniformly converted to a single unit before applying surface area or volume calculations.
- Understand curved vs. total surface area: The question will state whether it requires Curved Surface Area (CSA) or Total Surface Area (TSA) measurements because CSA excludes base(s) but TSA includes all surfaces.
- Practice real-life word problems: Specific questions about wall painting costs and tank water capacity require formula application to develop useful practical abilities.
NCERT Solutions for Class 9 Mathematics: Chapter-wise
We at Careers360 compiled all the NCERT class 9 Maths solutions in one place for easy student reference. The following links will allow you to access them.
Also, read,
- NCERT Notes Class 9 Maths Chapter 11 Surface Areas and Volumes
- NCERT Exemplar Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
NCERT Books and NCERT Syllabus
Students can use the following links to check the latest NCERT syllabus and read some reference books.
Frequently Asked Questions (FAQs)
This chapter covers surface areas and volumes of different 3D shapes, like spheres and right circular cones.
NCERT Solutions provide step-by-step explanations and solved examples that make the formulas and concepts of surface areas and volumes easy to understand.
Yes, exams often include direct application questions as well as word problems based on cone and sphere surface areas and volumes.
Yes, you can easily download the NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes in a free PDF format for offline study from various trusted educational sites such as Careers360.
The curved surface area (CSA) of a cone is given by πrl, where r is the radius and l is the slant height.
The total surface area (TSA) is πr(l + r).
Popular Questions
Courses After 12th
Study Resources, Applications and Opportunities
Take Aakash iACST and get instant scholarship on coaching programs.
NEET Most scoring concepts
Get nowThis ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
