NCERT Solutions for Class 9 Maths Chapter 10 Heron's Formula
In the world of triangles, Heron's Formula is the golden key to the unknown space within the triangle(s). Everyone knows their own ways of finding the area of a triangle, as intended, either through the general area triangle formula or the specially intended formula for an Equilateral triangle. Did you ever stop and ask yourself how you would find the area of a triangle if it were of a scalene nature (different lengths for all three sides), and you had zero idea how to find an altitude? That's where we turn to Heron's formula, and it helps us find the triangle's area. Heron's formula can be used in the actual world, and they can help us to figure out the area of irregular plots. Many teachers recommend NCERT Solutions because they closely match the exam pattern.
This Story also Contains
- Heron's Formula Class 9 Questions And Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 10 Heron's Formula: Exercise Questions
- Heron's Formula Class 9 NCERT Solutions: Exercise-wise
- Class 9 Maths NCERT Chapter 10: Extra Question
- Heron's Formula Class 9 Chapter 10: Topics
- NCERT Heron's Formula Class 9 Solutions - Important Formulae
- Approach to Solve Questions of Heron's Formula Class 9
- NCERT Solutions for Class 9 Mathematics: Chapter-wise
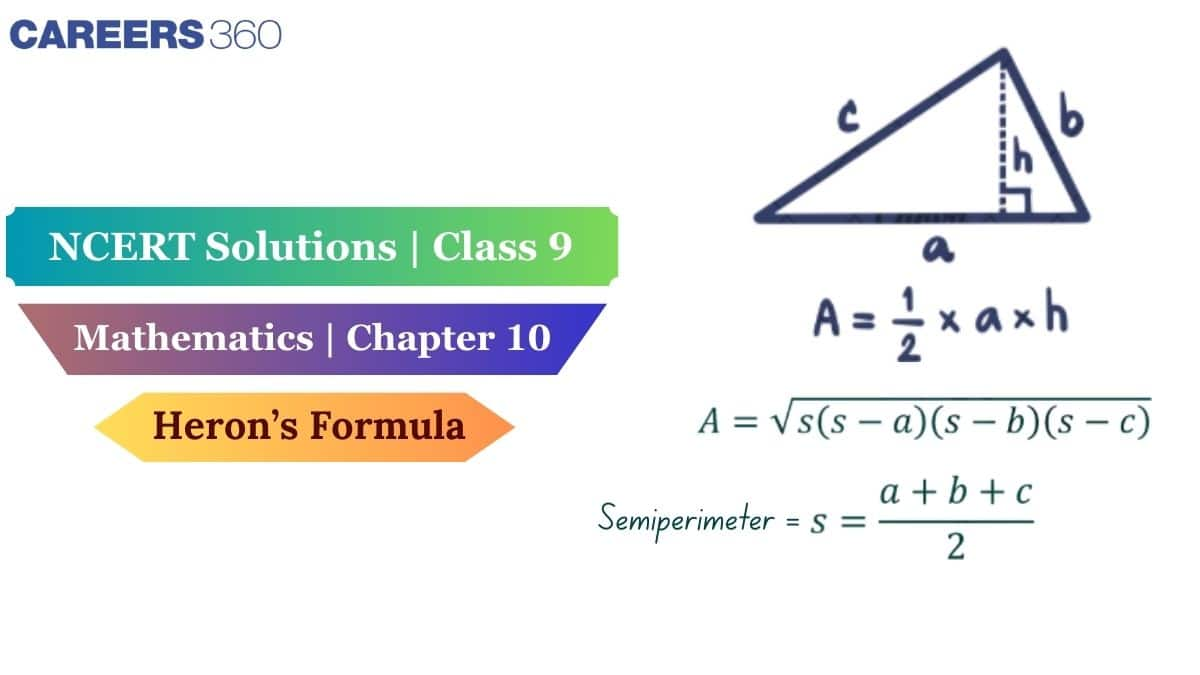
Heron’s formula is the poet's way of determining the area of a triangle. Heron's formula is not just important for grade 9 board exams, but also for higher grade tests and competitive exams. Students can make an effort to solve the exercises in the NCERT textbooks on their own before validating their answers with these well-constructed solutions. The latest NCERT solutions for Class 9 Maths not only deal with different types of triangles, but they also take the concept further to quadrilateral problem situations in the real world. An added benefit of the NCERT Solutions for Class 9 is to help students apply the formula correctly, especially under test conditions, although the application-based or word problems can also become test questions. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
Heron's Formula Class 9 Questions And Answers PDF Free Download
These NCERT Solutions for Class 9 Maths Chapter 10 Heron's Formula have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. You can also download the solutions in PDF format.
NCERT Solutions for Class 9 Maths Chapter 10 Heron's Formula: Exercise Questions
|
Class 9 Maths Chapter 10 Question Answers: Exercise: 10.1 |
Answer:
Given: The Perimeter of the equilateral triangle is 180 cm.
Therefore, each side of the triangle is:
$
a=\frac{180}{3}=60 \mathrm{~cm}
$
Now, calculate the semi-perimeter:
$
\mathrm{s}=\frac{\text { Perimeter }}{2}=\frac{180}{2}=90 \mathrm{~cm}
$
Use Heron's Formula to find the area, that is:
$
\text { Area }=\sqrt{s(s-a)(s-b)(s-c)}
$
Area
$=\sqrt{90(90-60)(90-60)(90-60)}$
$=\sqrt{90 \times 30 \times 30 \times 30}$
$=\sqrt{90 \times 27000}=\sqrt{2430000}=900 \sqrt{3} \mathrm{~cm}^2$
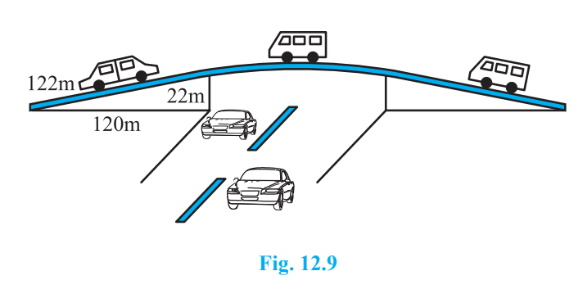
Answer:
From the figure,
Let the sides of the triangle be:
a = 122m, b = 120m and c = 22m
Therefore, the semi-perimeter, $s$, will be
$
s=\frac{a+b+c}{2}=\frac{122+120+22}{2}=\frac{264}{2}=132 m
$
Thus, Area ( using Heron's formula ):
$
\begin{aligned}
& A=\sqrt{s(s-a)(s-b)(s-c)} \\
& =\sqrt{132(132-122)(132-120)(132-22)} \mathrm{m}^2 \\
& =\sqrt{132(10)(12)(110)} \mathrm{m}^2 \\
& =\sqrt{(12 \times 11)(10)(12)(11 \times 10)} \mathrm{m}^2=1320 \mathrm{~m}^2
\end{aligned}
$
Given the rent for 1 year (i.e., 12 months) per square meter is Rs. 5000.
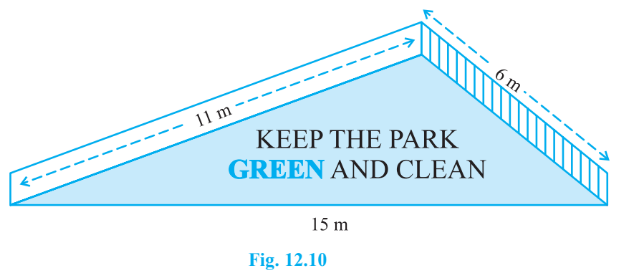
Answer:
We are given the sides of the triangle, which are:
a = 15 m, b = 11m and c = 6m
So, the semi-perimeter of the triangle will be:
$
s=\frac{a+b+c}{2}=\frac{15+11+6}{2}=\frac{32}{2}=16 \mathrm{~m}
$
Therefore, the area painted in colour is:
$
\begin{aligned}
& A=\sqrt{s(s-a)(s-b)(s-c)} \\
& =\sqrt{16(16-15)(16-11)(16-6)} \\
& =\sqrt{16(1)(5)(10)} \\
& =\sqrt{(4 \times 4)(1)(5)(5 \times 2)} \\
& =4 \times 5 \sqrt{2}=20 \sqrt{2} \mathrm{~m}^2
\end{aligned}
$
Question 4: Find the area of a triangle, two sides of which are 18 cm and 10 cm, and the perimeter is 42 cm.
Answer:
Given the perimeter of the triangle is 42 cm and the lengths of two sides, $\mathrm{a}=18 \mathrm{~cm}$ and $\mathrm{b}=10 \mathrm{~cm}$.
So, $a+b+c=42 c m$
$⇒c=42-18-10=14 \mathrm{~cm}$
Thus, the semi-perimeter of the triangle will be:
$
s=\frac{\text { Perimeter }}{2}=\frac{42 \mathrm{~cm}}{2}=21 \mathrm{~cm}
$
Therefore, the area given by the Heron's Formula will be,
$
\begin{aligned}
& A=\sqrt{s(s-a)(s-b)(s-c)} \\
& =\sqrt{21(21-18)(21-10)(21-14)} \\
& =\sqrt{(7 \times 3)(3)(11)(7)} \\
& =21 \sqrt{11} \mathrm{~cm}^2
\end{aligned}
$
Question 5: Sides of a triangle are in the ratio of 12 : 17 : 25, and its perimeter is 540 cm. Find its area.
Answer:
Given the sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm.
Let the length of one side of the triangle to be $a=12 x$
Then, the remaining two sides be $b=17 x$ and $c=25 x$.
Thus, by the given perimeter,
Perimeter $=a+b+c=12 x+17 x+25 x=540 c m$
$
\begin{aligned}
& \Longrightarrow 54 x=540 \mathrm{~cm} \\
& \Longrightarrow x=10
\end{aligned}
$
Therefore, the sides of the triangle are:
$
\begin{aligned}
& a=12 \times 10=120 \mathrm{~cm} \\
& b=17 \times 10=170 \mathrm{~cm}
\end{aligned}
$
$
c=25 \times 10=250 \mathrm{~cm}
$
The semi-perimeter of the triangle is:
$
s=\frac{540 \mathrm{~cm}}{2}=270 \mathrm{~cm}
$
Therefore, using Heron's Formula, the area of the triangle is:
$
\begin{aligned}
& A=\sqrt{s(s-a)(s-b)(s-c)} \\
& =\sqrt{270(270-120)(270-170)(270-250)} \\
& =\sqrt{270(150)(100)(20)} \\
& =\sqrt{81000000}=9000 \mathrm{~cm}^2
\end{aligned}
$
Answer:
Given, the perimeter of an isosceles triangle is 30 cm and the length of the sides which are equal is 12 cm.
Let the third side length be 'a cm '.
Then, Perimeter $=a+b+c$
$
\begin{aligned}
& \Rightarrow 30=a+12+12 \\
& \Rightarrow a=6 \mathrm{~cm}
\end{aligned}
$
So, the semi-perimeter of the triangle is:
$
s=\frac{\text { Perimeter }}{2}=\frac{1}{2} \times 30 \mathrm{~cm}=15 \mathrm{~cm}
$
Therefore, using Heron's Formula, the area of the triangle is:
$
\begin{aligned}
& A=\sqrt{s(s-a)(s-b)(s-c)} \\
& =\sqrt{15(15-6)(15-12)(15-12)} \\
& =\sqrt{15(9)(3)(3)} \\
& =9 \sqrt{15} \mathrm{~cm}^2
\end{aligned}
$
Heron's Formula Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Heron's Formula Class 9 Maths Chapter 10 are provided in the link below.
Class 9 Maths NCERT Chapter 10: Extra Question
Question: Find the area of a triangle whose sides are 9 cm, 10 cm, and 17 cm using Heron’s formula.
Answer:
Let the sides be $a=9 \mathrm{~cm}, b=10 \mathrm{~cm}, c=17 \mathrm{~cm}$
$
\begin{aligned}
& s=\frac{a+b+c}{2}=\frac{9+10+17}{2}=\frac{36}{2}=18 \mathrm{~cm} \\
& \text { Area }=\sqrt{s(s-a)(s-b)(s-c)}\\ &=\sqrt{18(18-9)(18-10)(18-17)} \\
& =\sqrt{18 \times 9 \times 8 \times 1}=\sqrt{1296}=36 \mathrm{~cm}^2
\end{aligned}
$
Heron's Formula Class 9 Chapter 10: Topics
Topics you will learn in NCERT Class 9 Maths Chapter 10 Heron's Formula include:
- Area of a Triangle — by Heron’s Formula
- Summary
NCERT Heron's Formula Class 9 Solutions - Important Formulae
Triangle
$
\text { Semi-perimeter of a triangle }=s=\frac{(a+b+c)}{2}
$
Where ' s ' is the semi-perimeter, and ' a ', ' b ', and ' c ' are the lengths of its sides.
Area $=\sqrt{s(s-a)(s-b)(s-c)}$
Equilateral Triangle
For an equilateral triangle with side length 'a':
-
Its perimeter is given by: Perimeter = 3a units.
-
The altitude (height) of an equilateral triangle is equal to$\frac{\sqrt{3}}{2}$ times its side length.
Altitude $=\frac{\sqrt{3}}{2} \times a$ units. -
The area of an equilateral triangle is equal to $\frac{\sqrt{3}}{4}$ times the square of its side length,
Area $=\frac{\sqrt{3}}{4} \times a^2$ units. These formulas are specific to equilateral triangles and are based on their unique properties.
Approach to Solve Questions of Heron's Formula Class 9
Using these approaches, students can tackle the Heron's Formula Class 9 Chapter 10 Question Answers with greater confidence.
1. Memorise the Heron’s Formula: Students need to remember the standard formula, which states Area equals the square root of semi-perimeter times its difference with each side. The formula uses "s" to denote the semi-perimeter of a triangle.
2. Calculate semi-perimeter accurately: The calculation of $s=\frac{a+b+c}2$ requires utmost attention because even minor errors can create problems throughout the problem-solving process.
3. Check if a triangle is valid: The triangle inequality rule should be used to verify triangle feasibility before you implement the formula.
4. Work with different triangle types: Apply Heron’s formula on various triangle shapes, including scalene, isosceles and right-angled to enhance your understanding of the concept.
5. Special attention must be given when simplifying square roots: Preparing the value inside the square root for calculation before extracting the root will reduce errors, particularly when working with irrational numbers.
6. Extend to real-world problems: When solving problems about land plots or uneven quadrilaterals, apply Heron’s rule by dividing the shape into two triangles.
NCERT Solutions for Class 9 Mathematics: Chapter-wise
We at Careers360 compiled all the NCERT class 9 Maths solutions in one place for easy student reference. The following links will allow you to access them.
Also, read,
- NCERT Notes Class 9 Maths Chapter 10 Heron's Formula
- NCERT Exemplar Solutions for Class 9 Maths Chapter 10 Heron's Formula
NCERT Books and NCERT Syllabus
The following links can be used to find the latest NCERT syllabus and some reference books. These are very useful study materials to do well in the exam.
Frequently Asked Questions (FAQs)
Q: Are NCERT solutions for Chapter 10 enough for exams?
A:
Yes. NCERT solutions provide detailed, step-by-step answers that are sufficient for school exams as well as for building a strong foundation for higher classes.
Q: Can Heron’s Formula be used for all types of triangles?
A:
Yes, it works for scalene, isosceles, and equilateral triangles. For right triangles, the standard base-height formula is shorter, but Heron’s formula still gives the same result.
Q: Where can I download NCERT Solutions for Class 9 Maths Chapter 10?
A:
Students can get free downloadable PDFs of NCERT Solutions for Class 9 Maths Chapter 10 Heron's Formula from various trusted educational websites, such as Careers360.
Q: What is Heron’s Formula as discussed in NCERT Class 9 Maths Chapter 10?
A:
Heron’s formula is used to find the area of a triangle when the lengths of all three sides are known. If sides are a, b, and c, then semi-perimeter(s) = (a + b + c) /2 and the area of the triangle = √ s(s - a) (s - b) (s - c)
Q: How does the NCERT solutions are helpful ?
A:
NCERT solutions are helpful for students who are unable to solve the NCERT textbook problems on their own. These solutions also provide detailed explanations, giving students conceptual clarity.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Study Resources, Applications and Opportunities
Take Aakash iACST and get instant scholarship on coaching programs.
NEET Most scoring concepts
Get nowThis ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE