NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles

Class 9 maths chapter 9 question answer - Exercise: 9.1

Q Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

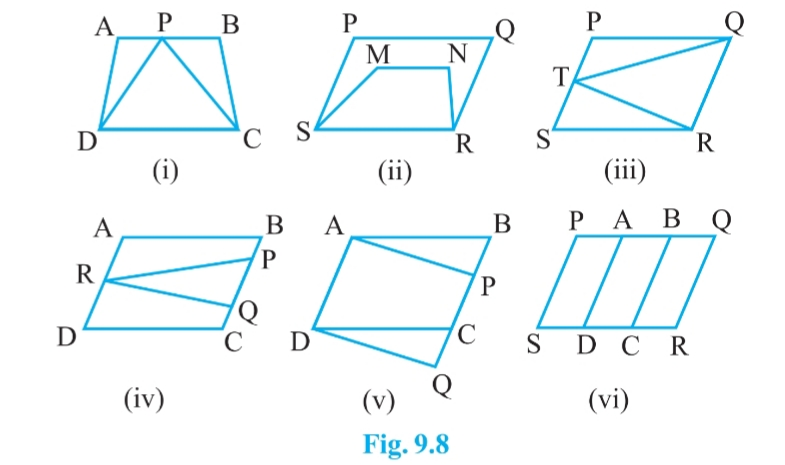
Answer:

In figure (i), (iii) and (v) we can see that. they lie on the same base and between the same parallel lines.
In figure (i) figure (iii) figure (v)
Common base DC QR AD
Two parallels DC and AB QR and PS AD and BQ

Class 9 areas of parallelograms and triangles NCERT solutions - Exercise : 9.2

Q1 In Fig. $\small 9.15$ , ABCD is a parallelogram, $\small AE\perp DC$ and $\small CF\perp AD$ . If $\small AB=16\hspace{1mm}cm$ , $\small AE=8\hspace{1mm}cm$ and $\small CF=10\hspace{1mm}cm$ , find AD.

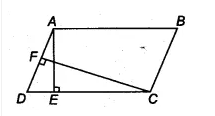
Answer:

We have,
AE $\perp$ DC and CF $\perp$ AD
AB = 16 cm, AE = 8 cm and CF = 10 cm

Since ABCD is a parallelogram,
therefore, AB = DC = 16 cm
We know that, area of parallelogram (ABCD) = base . height
= CD $\times$ AE = (16 $\times$ 8 ) $cm^2$
SInce, CF $\perp$ AD
therefore area of parallelogram = AD $\times$ CF = 128 $cm^2$
= AD = 128/10
= AD = 12.8 cm

Thus the required length of AD is 12.8 cm.

Q2 If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that

$\small ar(EFGH)=\frac{1}{2}ar(ABCD)$

Answer:

Join GE and HE,
Since F, F, G, H are the mid-points of the parallelogram ABCD. Therefore, GE || BC ||AD and HF || DC || AB.
It is known that if a triangle and the parallelogram are on the same base and between the same parallel lines. then the area of the triangle is equal to the half of the area of the parallelogram.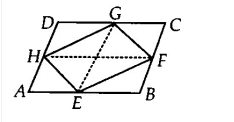

Now, $\Delta$ EFG and ||gm BEGC are on the same base and between the same parallels EG and BC.
Therefore, ar ( $\Delta$ EFG) = $1/2$ ar (||gm BEGC)...............(i)
Similarly, ar ( $\Delta$ EHG) = 1/2 . ar(||gm AEGD)..................(ii)
By adding eq (i) and eq (ii), we get

ar ( $\Delta$ EFG) + ar ( $\Delta$ EHG) = 1/2 (ar (||gm BEGC) + ar(||gm AEGD))
ar (EFGH) = 1/2 ar(ABCD)
Hence proved

Q3 P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that $\small ar(APB)=ar(BCQ)$ .

Answer:

We have,
ABCD is a parallelogram, therefore AB || CD and BC || AD.

Now, $\Delta$ APB and ||gm ABCD are on the same base AB and between two parallels AB and DC.
Therefore, ar ( $\Delta$ APB) = 1/2 . ar(||gm ABCD)...........(i)

Also, $\Delta$ BQC and ||gm ABCD are on the same base BC and between two parallels BC and AD.
Therefore, ar( $\Delta$ BQC) = 1/2 . ar(||gmABCD)...........(ii)

From eq(i) and eq (ii), we get,
ar ( $\Delta$ APB) = ar( $\Delta$ BQC)
Hence proved.

Q4 (i) In Fig. $9.16$ , P is a point in the interior of a parallelogram ABCD. Show that
$\small ar(APB)+ar(PCD) = \frac{1}{2}ar(ABCD)$

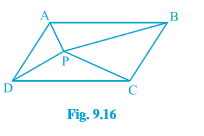
[ Hint : Through P, draw a line parallel to AB.]

Answer:

We have a ||gm ABCD and AB || CD, AD || BC. Through P, draw a line parallel to AB
Now, $\Delta$ APB and ||gm ABEFare on the same base AB and between the same parallels EF and AB.
Therefore, ar ( $\Delta$ APB) = 1/2 . ar(ABEF)...............(i)
Similarly, ar ( $\Delta$ PCD ) = 1/2 . ar (EFDC) ..............(ii)
Now, by adding both equations, we get
$\small ar(APB)+ar(PCD) = \frac{1}{2}ar(ABCD)$

Hence proved.

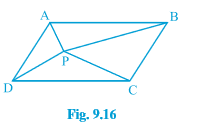
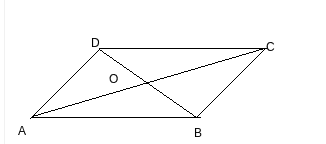
Q4 (ii) In Fig. $\small 9.16$ , P is a point in the interior of a parallelogram ABCD. Show that

$\small ar(APD)+ar(PBC)=ar(APB)+ar(PCD)$

[ Hint: Through P, draw a line parallel to AB.]

Answer:

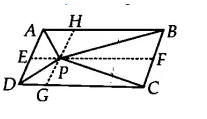
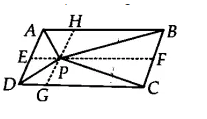
We have a ||gm ABCD and AB || CD, AD || BC. Through P, draw a line parallel to AB
Now, $\Delta$ APD and ||gm ADGHare on the same base AD and between the same parallels GH and AD.
Therefore, ar ( $\Delta$ APD) = 1/2 . ar(||gm ADGH).............(i)

Similarily, ar ( $\Delta$ PBC) = 1/2 . ar(||gm BCGH)............(ii)

By adding the equation i and eq (ii), we get

$\small ar(APD)+ar(PBC)=ar(APB)+ar(PCD)$

Hence proved.

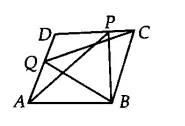
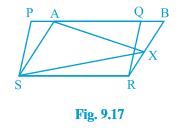
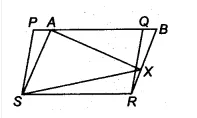
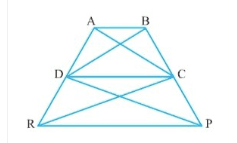
Q5 In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that

(i) $\small ar(PQRS)=ar(ABRS)$
(ii) $\small ar(AXS)=\frac{1}{2}ar(PQRS)$

Answer:

(i) Parallelogram PQRS and ABRS are on the same base RS and between the same parallels RS and PB.
Therefore, $\small ar(PQRS)=ar(ABRS)$ ............(i)
Hence proved

(ii) $\Delta$ AXS and ||gm ABRS are on the same base AS and between same parallels AS and RB.
Therefore, ar ( $\Delta$ AXS) = 1/2 . ar(||gm ABRS)............(ii)

Now, from equation (i) and equation (ii), we get

$\small ar(AXS)=\frac{1}{2}ar(PQRS)$

Hence proved.

Q6 A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

Answer:

We have a field in the form of parallelogram PQRS and a point A is on the side RS. Join AP and AQ. The field is divided into three parts i.e, $\Delta$ APS, $\Delta$ QAR and $\Delta$ PAQ.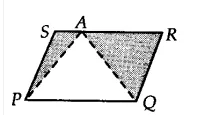

Since $\Delta$ APQ and parallelogram, PQRS is on the same base PQ and between same parallels RS and PQ.
Therefore, $ar(\Delta APQ) = \frac{1}{2}ar(PQRS)$ ............(i)
We can write above equation as,

ar (||gm PQRS) - [ar ( $\Delta$ APS) + ar( $\Delta$ QAR)] = 1/2 .ar(PQRS)
$\Rightarrow ar(\Delta APS)+ar(\Delta QAR) = \frac{1}{2}ar(PQRS)$
from equation (i),
$\Rightarrow ar(\Delta APS)+ar(\Delta QAR) =ar(\Delta APQ)$

Hence, she can sow wheat in $\Delta$ APQ and pulses in [ $\Delta$ APS + $\Delta$ QAR] or wheat in [ $\Delta$ APS + $\Delta$ QAR] and pulses in $\Delta$ APQ.

Class 9 maths chapter 9 NCERT solutions - exercise : 9.3

Q1 In Fig. $\small 9.23$ , E is any point on median AD of a $\small \Delta ABC$ . Show that. $\small ar(ABE)=ar(ACE)$

Answer:
We have $\Delta$ ABC such that AD is a median. And we know that median divides the triangle into two triangles of equal areas.
Therefore, ar( $\Delta$ ABD) = ar( $\Delta$ ACD)............(i)

Similarly, In triangle $\Delta$ BEC,
ar( $\Delta$ BED) = ar ( $\Delta$ DEC)................(ii)

On subtracting eq(ii) from eq(i), we get
ar( $\Delta$ ABD) - ar( $\Delta$ BED) =
$\small ar(ABE)=ar(ACE)$

Hence proved.

Q2 In a triangle ABC, E is the mid-point of median AD. Show that $\small ar(BED)=\frac{1}{4}ar(ABC)$ .

Answer:

We have a triangle ABC and AD is a median. Join B and E.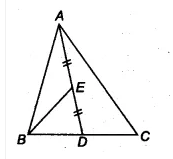

Since the median divides the triangle into two triangles of equal area.
$\therefore$ ar( $\Delta$ ABD) = ar ( $\Delta$ ACD) = 1/2 ar( $\Delta$ ABC)..............(i)
Now, in triangle $\Delta$ ABD,
BE is the median [since E is the midpoint of AD]
$\therefore$ ar ( $\Delta$ BED) = 1/2 ar( $\Delta$ ABD)........(ii)

From eq (i) and eq (ii), we get

ar ( $\Delta$ BED) = 1/2 . (1/2 ar(ar ( $\Delta$ ABC))
ar ( $\Delta$ BED) = 1/4 .ar( $\Delta$ ABC)

Hence proved.

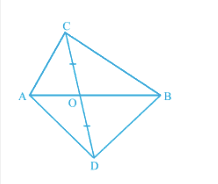
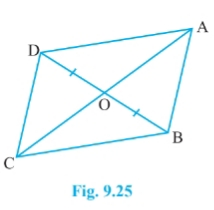
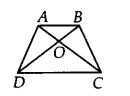
Q3 Show that the diagonals of a parallelogram divide it into four triangles of equal area.

Answer:

Let ABCD is a parallelogram. So, AB || CD and AD || BC and we know that Diagonals bisects each other. Therefore, AO = OC and BO = OD

Since OD = BO
Therefore, ar ( $\Delta$ BOC) = ar ( $\Delta$ DOC)...........(a) ( since OC is the median of triangle CBD)

Similarly, ar( $\Delta$ AOD) = ar( $\Delta$ DOC) ............(b) ( since OD is the median of triangle ACD)

and, ar ( $\Delta$ AOB) = ar( $\Delta$ BOC)..............(c) ( since OB is the median of triangle ABC)

From eq (a), (b) and eq (c), we get

ar ( $\Delta$ BOC) = ar ( $\Delta$ DOC)= ar( $\Delta$ AOD) = ( $\Delta$ AOB)

Thus, the diagonals of ||gm divide it into four equal triangles of equal area.

Q4 In Fig. $\small 9.24$ , ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that $\small ar(ABC)=ar(ABD)$ .

Answer:

We have, $\Delta$ ABC and $\Delta$ ABD on the same base AB. CD is bisected by AB at point O.
$\therefore$ OC = OD
Now, in $\Delta$ ACD, AO is median
$\therefore$ ar ( $\Delta$ AOC) = ar ( $\Delta$ AOD)..........(i)

Similarly, in $\Delta$ BCD, BO is the median
$\therefore$ ar ( $\Delta$ BOC) = ar ( $\Delta$ BOD)............(ii)

Adding equation (i) and eq (ii), we get

ar ( $\Delta$ AOC) + ar ( $\Delta$ BOC) = ar ( $\Delta$ AOD) + ar ( $\Delta$ BOD)

$\small ar(ABC)=ar(ABD)$

Hence proved.

Q5 (i) D, E and F are respectively the mid-points of the sides BC, CA and AB of a $\small \Delta ABC$ . Show that BDEF is a parallelogram.

Answer:

We have a triangle $\Delta$ ABC such that D, E and F are the midpoints of the sides BC, CA and AB respectively.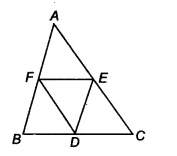

Now, in $\Delta$ ABC,
F and E are the midpoints of the side AB and AC.
Therefore according to mid-point theorem, the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half of the third side.
$\therefore$ EF || BC or EF || BD

also, EF = 1/2 (BC)
$\Rightarrow EF = BD$ [ D is the midpoint of BC]
Similarly, ED || BF and ED = FB
Hence BDEF is a parallelogram.

Q5 (ii) D, E and F are respectively the mid-points of the sides BC, CA and AB of a $\small \Delta ABC$ . Show that

$\small ar(DEF)=\frac{1}{4}ar(ABC)$

Answer:

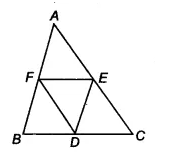
We already proved that BDEF is a ||gm.
Similarly, DCEF and DEAF are also parallelograms.
Now, ||gm BDEF and ||gm DCEF is on the same base EF and between same parallels BC and EF
$\therefore$ Ar (BDEF) = Ar (DCEF)
$\Rightarrow$ Ar( $\Delta$ BDF) = Ar ( $\Delta$ DEF) .............(i)

It is known that diagonals of ||gm divides it into two triangles of equal area.
$\therefore$ Ar(DCE) = Ar (DEF).......(ii)

and, Ar( $\Delta$ AEF) = Ar ( $\Delta$ DEF)...........(iii)

From equation(i), (ii) and (iii), we get

Ar( $\Delta$ BDF) = Ar(DCE) = Ar( $\Delta$ AEF) = Ar ( $\Delta$ DEF)

Thus, Ar ( $\Delta$ ABC) = Ar( $\Delta$ BDF) + Ar(DCE) + Ar( $\Delta$ AEF) + Ar ( $\Delta$ DEF)
Ar ( $\Delta$ ABC) = 4 . Ar( $\Delta$ DEF)
$\Rightarrow$ $ar(\Delta DEF) = \frac{1}{4}ar(\Delta ABC)$

Hence proved.

Q5 (iii) D, E and F are respectively the mid-points of the sides BC, CA and AB of a $\small \Delta ABC$ . Show that

$\small ar(BDEF)=\frac{1}{2}ar(ABC)$

Answer:

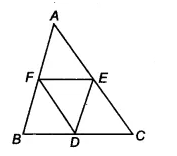
Since we already proved that,
ar( $\Delta$ DEF) = ar ( $\Delta$ BDF).........(i)

So, ar(||gm BDEF) = ar( $\Delta$ BDF) + ar ( $\Delta$ DEF)
= 2 . ar( $\Delta$ DEF) [from equation (i)]
$\\= 2[\frac{1}{4}ar(\Delta ABC)]\\ =\frac{1}{2} ar(\Delta ABC)$

Hence proved.

Q6 (i) In Fig. $\small 9.25$ , diagonals AC and BD of quadrilateral ABCD intersect at O such that. If $\small AB=CD$ , then show that:

$\small ar(DOC)=ar(AOB)$

[ Hint: From D and B, draw perpendiculars to AC.]

Answer:
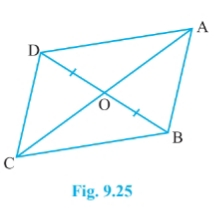
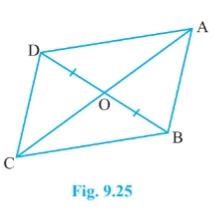
We have ABCD is quadrilateral whose diagonals AC and BD intersect at O. And OB = OD, AB = CD
Draw DE $\perp$ AC and FB $\perp$ AC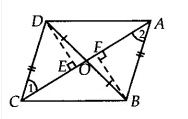

In $\Delta$ DEO and $\Delta$ BFO
$\angle$ DOE = $\angle$ BOF [vertically opposite angle]
$\angle$ OED = $\angle$ BFO [each $90^0$ ]
OB = OD [given]

Therefore, by AAS congruency
$\Delta$ DEO $\cong$ $\Delta$ BFO
$\Rightarrow$ DE = FB [by CPCT]

and ar( $\Delta$ DEO) = ar( $\Delta$ BFO) ............(i)

Now, In $\Delta$ DEC and $\Delta$ ABF
$\angle$ DEC = $\angle$ BFA [ each $90^0$ ]
DE = FB
DC = BA [given]
So, by RHS congruency
$\Delta$ DEC $\cong$ $\Delta$ BFA
$\angle$ 1 = $\angle$ 2 [by CPCT]
and, ar( $\Delta$ DEC) = ar( $\Delta$ BFA).....(ii)

By adding equation(i) and (ii), we get
$\small ar(DOC)=ar(AOB)$
Hence proved.

Q6 (ii) In Fig. $\small 9.25$ , diagonals AC and BD of quadrilateral ABCD intersect at O such that $\small OB=OD$ . If $\small AB=CD$ , then show that: $\small ar(DCB)=ar(ACB)$

[ Hint: From D and B, draw perpendiculars to AC.]

Answer:

We already proved that,
$ar(\Delta DOC)=ar(\Delta AOB)$
Now, add $ar(\Delta BOC)$ on both sides we get

$\\ar(\Delta DOC)+ar(\Delta BOC)=ar(\Delta AOB)+ar(\Delta BOC)\\ ar(\Delta DCB) = ar (\Delta ACB)$
Hence proved.

Q6 (iii) In Fig. $\small 9.25$ , diagonals AC and BD of quadrilateral ABCD intersect at O such that $\small OB=OD$ . If $\small AB=CD$ , then show that:

$\small DA\parallel CB$ or ABCD is a parallelogram.

[ Hint : From D and B, draw perpendiculars to AC.]

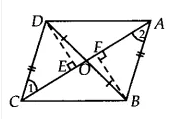
Answer:

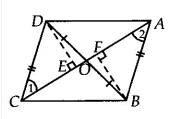
Since $\Delta$ DCB and $\Delta$ ACB both lie on the same base BC and having equal areas.
Therefore, They lie between the same parallels BC and AD
$\Rightarrow$ CB || AD
also $\angle$ 1 = $\angle$ 2 [ already proved]
So, AB || CD
Hence ABCD is a || gm

Q7 D and E are points on sides AB and AC respectively of $\small \Delta ABC$ such that $\small ar(DBC)=ar(EBC)$ . Prove that $\small DE\parallel BC$ .

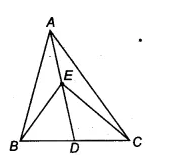
Answer:

We have $\Delta$ ABC and points D and E are on the sides AB and AC such that ar( $\Delta$ DBC ) = ar ( $\Delta$ EBC)


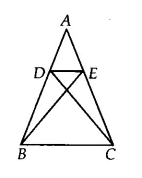
Since $\Delta$ DBC and $\Delta$ EBC are on the same base BC and having the same area.
$\therefore$ They must lie between the same parallels DE and BC
Hence DE || BC.

Q8 XY is a line parallel to side BC of a triangle ABC. If $\small BE\parallel AC$ and $\small CF\parallel AB$ meet XY at E and F respectively, show that $\small ar(ABE)=ar(ACF)$

Answer:

We have a $\Delta$ ABC such that BE || AC and CF || AB
Since XY || BC and BE || CY
Therefore, BCYE is a ||gm
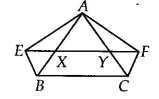Now, The ||gm BCEY and $\Delta$ ABE are on the same base BE and between the same parallels AC and BE.
$\therefore$ ar( $\Delta$ AEB) = 1/2 .ar(||gm BEYC)..........(i)
Similarly, ar( $\Delta$ ACF) = 1/2 . ar(||gm BCFX)..................(ii)

Also, ||gm BEYC and ||gmBCFX are on the same base BC and between the same parallels BC and EF.
$\therefore$ ar (BEYC) = ar (BCFX).........(iii)

From eq (i), (ii) and (iii), we get

ar( $\Delta$ ABE) = ar( $\Delta$ ACF)
Hence proved.

Q9 The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Fig. $\small 9.26$ ). Show that $\small ar(ABCD)=ar(PBQR)$ . [ Hint: Join AC and PQ. Now compare $\small ar(ACQ)$ and $\small ar(APQ)$ .]

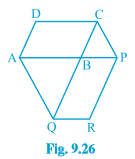Answer:

Join the AC and PQ.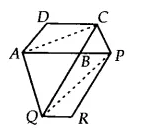

It is given that ABCD is a ||gm and AC is a diagonal of ||gm
Therefore, ar( $\Delta$ ABC) = ar( $\Delta$ ADC) = 1/2 ar(||gm ABCD).............(i)

Also, ar( $\Delta$ PQR) = ar( $\Delta$ BPQ) = 1/2 ar(||gm PBQR).............(ii)

Since $\Delta$ AQC and $\Delta$ APQ are on the same base AQ and between same parallels AQ and CP.
$\therefore$ ar( $\Delta$ AQC) = ar ( $\Delta$ APQ)

Now, subtracting $\Delta$ ABQ from both sides we get,

ar( $\Delta$ AQC) - ar ( $\Delta$ ABQ) = ar ( $\Delta$ APQ) - ar ( $\Delta$ ABQ)
ar( $\Delta$ ABC) = ar ( $\Delta$ BPQ)............(iii)

From eq(i), (ii) and (iii) we get

$\small ar(ABCD)=ar(PBQR)$

Hence proved.

Q10 Diagonals AC and BD of a trapezium ABCD with $\small AB\parallel DC$ intersect each other at O. Prove that $\small ar(AOD)=ar(BOC)$ .

Answer:

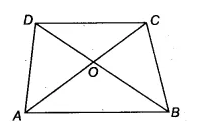
We have a trapezium ABCD such that AB || CD and it's diagonals AC and BD intersect each other at O
$\Delta$ ABD and $\Delta$ ABC are on the same base AB and between same parallels AB and CD
$\therefore$ ar( $\Delta$ ABD) = ar ( $\Delta$ ABC)

Now, subtracting $\Delta$ AOB from both sides we get

ar ( $\Delta$ AOD) = ar ( $\Delta$ BOC)

Hence proved.

Q11 In Fig. $\small 9.27$ , ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

(i) $\small ar(ACB)=ar(ACF)$
(ii) $\small ar(AEDF)=ar(ABCDE)$

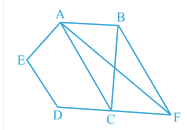
Answer:
We have a pentagon ABCDE in which BF || AC and CD is produced to F.

(i) Since $\Delta$ ACB and $\Delta$ ACF are on the same base AC and between same parallels AC and FB.
$\therefore$ ar( $\Delta$ ACB) = ar ( $\Delta$ ACF)..................(i)

(ii) Adding the ar (AEDC) on both sides in equation (i), we get

ar( $\Delta$ ACB) + ar(AEDC) = ar ( $\Delta$ ACF) + ar(AEDC)
$\therefore$ $\small ar(AEDF)=ar(ABCDE)$

Hence proved.

Q12 A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.

Answer:

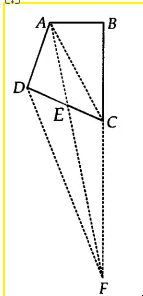
We have a quadrilateral shaped plot ABCD. Draw DF || AC and AF || CF.
Now, $\Delta$ DAF and $\Delta$ DCF are on the same base DF and between same parallels AC and DF.
$\therefore$ ar ( $\Delta$ DAF) = ar( $\Delta$ DCF)
On subtracting $\Delta$ DEF from both sides, we get

ar( $\Delta$ ADE) = ar( $\Delta$ CEF)...............(i)
The portion of $\Delta$ ADE can be taken by the gram panchayat and on adding the land $\Delta$ CEF to his (Itwaari) land so as to form a triangular plot.( $\Delta$ ABF)

We need to prove that ar( $\Delta$ ABF) = ar (quad. ABCD)

Now, adding ar(quad. ABCE) on both sides in eq (i), we get

ar ( $\Delta$ ADE) + ar(quad. ABCE) = ar( $\Delta$ CEF) + ar(quad. ABCE)
ar (ABCD) = ar( $\Delta$ ABF)

Q13 ABCD is a trapezium with $\small AB\parallel DC$ . A line parallel to AC intersects AB at X and BC at Y. Prove that $\small ar(ADX)=ar(ACY)$ . [ Hint: Join CX.]

Answer:

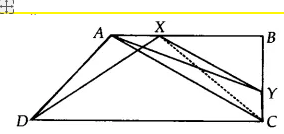
We have a trapezium ABCD, AB || CD
XY ||AC meets AB at X and BC at Y. Join XC

Since $\Delta$ ADX and $\Delta$ ACX lie on the same base CD and between same parallels AX and CD
Therefore, ar( $\Delta$ ADX) = ar( $\Delta$ ACX)..........(i)
Similarly ar( $\Delta$ ACX) = ar( $\Delta$ ACY).............(ii) [common base AC and AC || XY]
From eq (i) and eq (ii), we get

ar( $\Delta$ ADX) = ar ( $\Delta$ ACY)

Hence proved.

Q14 In Fig. $\small 9.28$ , $\small AP\parallel BQ\parallel CR$ . Prove that $\small ar(AQC)=ar(PBR)$ .

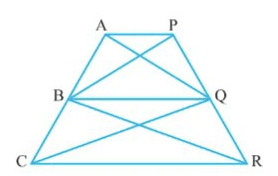
Answer:

We have, AP || BQ || CR
$\Delta$ BCQ and $\Delta$ BQR lie on the same base (BQ) and between same parallels (BQ and CR)
Therefore, ar ( $\Delta$ BCQ) = ar ( $\Delta$ BQR)........(i)

Similarly, ar ( $\Delta$ ABQ) = ar ( $\Delta$ PBQ) [common base BQ and BQ || AP]............(ii)

Add the eq(i) and (ii), we get

ar ( $\Delta$ AQC) = ar ( $\Delta$ PBR)

Hence proved.

Q15 Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that $\small ar(AOD)=ar(BOC)$ . Prove that ABCD is a trapezium.

Answer:

We have,
ABCD is a quadrilateral and diagonals AC and BD intersect at O such that ar( $\Delta$ AOD) = ar ( $\Delta$ BOC) ...........(i)

Now, add ar ( $\Delta$ BOA) on both sides, we get

ar( $\Delta$ AOD) + ar ( $\Delta$ BOA) = ar ( $\Delta$ BOA) + ar ( $\Delta$ BOC)
ar ( $\Delta$ ABD) = ar ( $\Delta$ ABC)
Since the $\Delta$ ABC and $\Delta$ ABD lie on the same base AB and have an equal area.
Therefore, AB || CD

Hence ABCD is a trapezium.

Q16 In Fig. $\small 9.29$ , $\small ar(DRC)=ar(DPC)$ and $\small ar(BDP)=ar(ARC)$ . Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Answer:

Given,
ar( $\Delta$ DPC) = ar( $\Delta$ DRC) ..........(i)
and ar( $\Delta$ BDP) = ar(ARC)............(ii)

from equation (i),
Since $\Delta$ DRC and $\Delta$ DPC lie on the same base DC and between same parallels.
$\therefore$ CD || RP (opposites sides are parallel)

Hence quadrilateral DCPR is a trapezium

Now, by subtracting eq(ii) - eq(i) we get

ar( $\Delta$ BDP) - ar( $\Delta$ DPC) = ar( $\Delta$ ARC) - ar( $\Delta$ DRC)
ar( $\Delta$ BDC) = ar( $\Delta$ ADC) (Since theya are on the same base DC)
$\Rightarrow$ AB || DC

Hence ABCD is a trapezium.

Areas of parallelograms and triangles class 9 solutions - Exercise : 9.4

Q1 Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Answer:

We have ||gm ABCD and a rectangle ABEF both lie on the same base AB such that, ar(||gm ABCD) = ar(ABEF)
for rectangle, AB = EF
and for ||gm AB = CD
$\Rightarrow$ CD = EF
$\Rightarrow$ AB + CD = AB + EF ...........(i)

SInce $\Delta$ BEC and $\Delta$ AFD are right angled triangle
Therefore, AD > AF and BC > BE
$\Rightarrow$ (BC + AD ) > (AF + BE)...........(ii)

Adding equation (i) and (ii), we get

(AB + CD)+(BC + AD) > (AB + BE) + (AF + BE)
$\Rightarrow$ (AB + BC + CD + DA) > (AB + BE + EF + FA)
Hence proved, perimeter of ||gm ABCD is greater than perimeter of rectangle ABEF.

Q2 In Fig. $\small 9.30$ , D and E are two points on BC such that $\small BD=DE=EC$ . Show that $\small ar(ABD)=ar(ADE)=ar(AEC)$ .

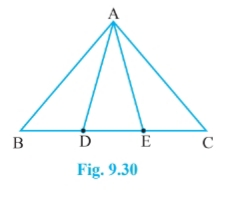
Answer:

In $\Delta$ ABC, D and E are two points on BC such that BD = DE = EC

AD is the median of ABE, therefore,

area of ABD= area of AED...................(1)

AE is the median of ACD, therefore,

area of AEC= area of AED...................(2)

From (1) and (2)

area of ABD=area of AED= area of AEC
Hence proved.

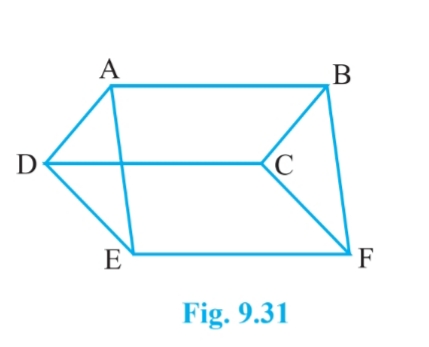
Q3 In Fig. $\small 9.31$ , ABCD, DCFE and ABFE are parallelograms. Show that $\small ar(ADE)=ar(BCF)$ .

Answer:

Given,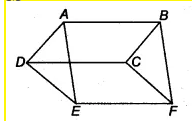

ABCD is a parallelogram. Therefore, AB = CD & AD = BC & AB || CD .......(i)

Now, $\Delta$ ADE and $\Delta$ BCF are on the same base AD = BC and between same parallels AB and EF.
Therefore, ar ( $\Delta$ ADE) = ar( $\Delta$ BCF)

Hence proved.

Q4 In Fig. $\small 9.32$ , ABCD is a parallelogram and BC is produced to a point Q such that $\small AD=CQ$ . If AQ intersects DC at P, show that $\small ar (BPC) = ar (DPQ)$ . [ Hint : Join AC.]

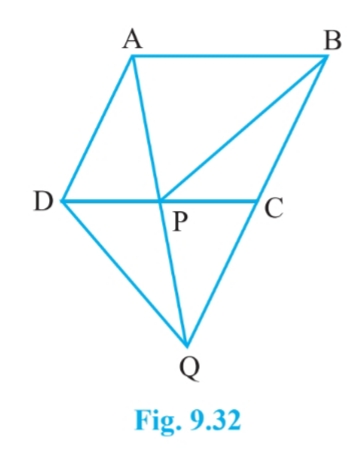Answer:

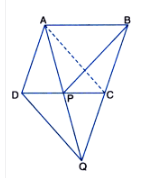
Given,
ABCD is a ||gm and AD = CQ. Join AC.
Since $\Delta$ DQC and $\Delta$ ACD lie on the same base QC and between same parallels AD and QC.
Therefore, ar( $\Delta$ DQC) = ar( $\Delta$ ACD).......(i)

Subtracting ar( $\Delta$ PQC) from both sides in eq (i), we get
ar( $\Delta$ DPQ) = ar( $\Delta$ PAC).............(i)

Since $\Delta$ PAC and $\Delta$ PBC are on the same base PC and between same parallel PC and AB.
Therefore, ar( $\Delta$ PAC) = ar( $\Delta$ PBC)..............(iii)

From equation (ii) and eq (ii), we get

$\small ar (BPC) = ar (DPQ)$

Hence proved.

Q5 (i) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

$\small ar(BDE)=\frac{1}{4}ar(ABC)$

[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

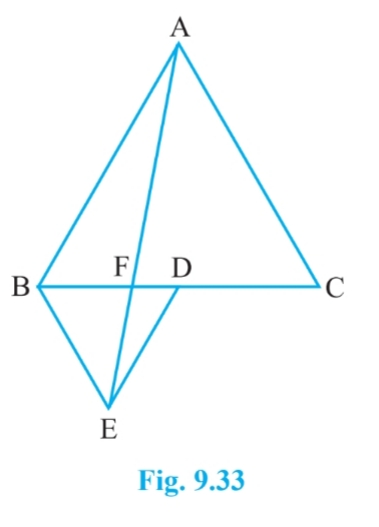Answer:

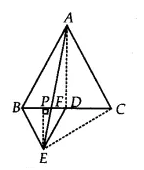
Let join the CE and AD and draw $EP \perp BC$ . It is given that $\Delta$ ABC and $\Delta$ BDE is an equilateral triangle.
So, AB =BC = CA = $a$ and D i sthe midpoint of BC
therefore, $BD = \frac{a}{2}= DE = BE$
(i) Area of $\Delta$ ABC = $\frac{\sqrt{3}}{4}a^2$ and
Area of $\Delta$ BDE = $\frac{\sqrt{3}}{4}(\frac{a}{2})^2= \frac{\sqrt{3}}{16}a^2$

Hence, $\small ar(BDE)=\frac{1}{4}ar(ABC)$

Q5 (ii) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BDE)=\frac{1}{2}ar(BAE)$

[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

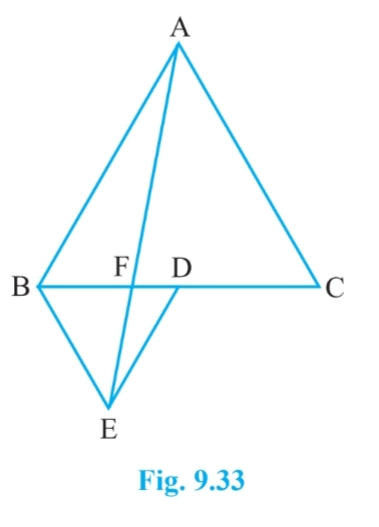
Answer:

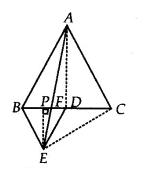
Since $\Delta$ ABC and $\Delta$ BDE are equilateral triangles.
Therefore, $\angle$ ACB = $\angle$ DBE = $60^0$
$\Rightarrow$ BE || AC

$\Delta$ BAE and $\Delta$ BEC are on the same base BE and between same parallels BE and AC.
Therefore, ar ( $\Delta$ BAE) = ar( $\Delta$ BEC)
$\Rightarrow$ ar( $\Delta$ BAE) = 2 ar( $\Delta$ BED) [since D is the meian of $\Delta$ BEC ]
$\Rightarrow$ $\small ar(BDE)=\frac{1}{2}ar(BAE)$
Hence proved.

Q5 (iii) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(ABC)=2ar(BEC)$

[ Hint : Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

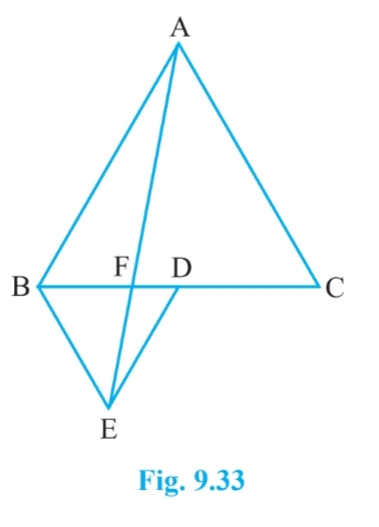
Answer:

We already proved that,
ar( $\Delta$ ABC) = 4.ar( $\Delta$ BDE) (in part 1)
and, ar( $\Delta$ BEC) = 2. ar( $\Delta$ BDE) (in part ii )

$\Rightarrow$ ar( $\Delta$ ABC) = 2. ar( $\Delta$ BEC)

Hence proved.

Q5 (iv) In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BFE)=ar(AFD)$
[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

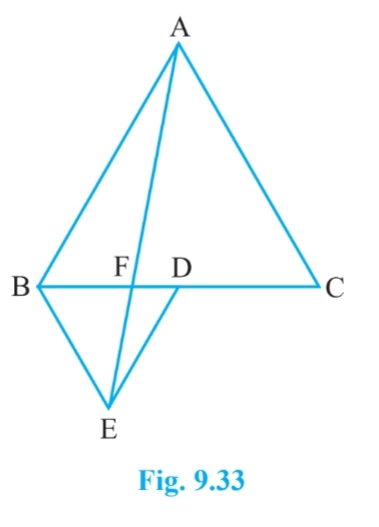
Answer:

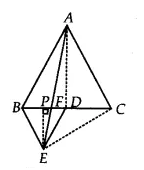
Since $\Delta$ ABC and $\Delta$ BDE are equilateral triangles.
Therefore, $\angle$ ACB = $\angle$ DBE = $60^0$
$\Rightarrow$ BE || AC

$\Delta$ BDE and $\Delta$ AED are on the same base ED and between same parallels AB and DE.
Therefore, ar( $\Delta$ BED) = ar( $\Delta$ AED)

On subtracting $\Delta$ EFD from both sides we get

$\small ar(BFE)=ar(AFD)$

Hence proved.

Q5 (v) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BFE)=2ar(FED)$

[ Hint : Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

Answer:

In right angled triangle $\Delta$ ABD, we get

$\\AB^2 = AD^2+BD^2\\ AD^2 = AB^2-BD^2$
$=a^2 - \frac{a^2}{4}=\frac{3a^2}{4}$
$AD=\frac{\sqrt{3}a}{2}$

So, in $\Delta$ PED,
$PE^2 = DE^2-DP^2$
$\\=(\frac{a}{2})^2-(\frac{a}{4})^2\\ =\frac{3a^2}{16}$
So, $PE=\frac{\sqrt{3}a}{4}$

Therefore, the Area of $\Delta AFD =1/2 (FD)\frac{\sqrt{3}a}{2}$ ..........(i)

And, Area of triangle $\Delta EFD =1/2 (FD)\frac{\sqrt{3}a}{4}$ ...........(ii)

From eq (i) and eq (ii), we get
ar( $\Delta$ AFD) = 2. ar( $\Delta$ EFD)
Since ar( $\Delta$ AFD) = ar( $\Delta$ BEF)

$\Rightarrow$ $\small ar(BFE)=2ar(FED)$

Q5 (vi) In Fig. $9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$ar (FED) = \frac{1}{8} ar (AFC)$

[ Hint: Join EC and AD. Show that $BE\parallel AC$ and $DE\parallel AB$ , etc.]

Answer:

$ar(\Delta AFC) =$
$\\= ar(\Delta AFD) + ar(\Delta ADC)\\ = ar(\Delta BFE) + 1/2. ar(\Delta ABC)\\ = ar(\Delta BFE) + 1/2\times [4\times ar(\Delta BDE)]\\ = ar(\Delta BFE) + 2\times ar(\Delta BDE)$
$= 2\times ar (\Delta FED) + 2\times [ar(\Delta BFE) + ar(\Delta FED)]$ .....(from part (v) ar( $\Delta$ BFE) = 2. ar( $\Delta$ FED) ]
$\\=2ar(\Delta FED) + 2[3\times ar(\Delta FED)]\\ =8\times ar(\Delta FED)$

$ar (FED) = \frac{1}{8} ar (AFC)$
Hence proved.

Q6 Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that $ar (APB) \times ar (CPD) = ar (APD) \times ar (BPC).$

[ Hint: From A and C, draw perpendiculars to BD.]

Answer:

Given that,
A quadrilateral ABCD such that it's diagonal AC and BD intersect at P. Draw $AM \perp BD$ and $CN \perp BD$

Now, ar( $\Delta$ APB) = $\frac{1}{2}\times BP\times AM$ and,
$ar(\Delta CDP)=\frac{1}{2}\times DP\times CN$
Therefore, ar( $\Delta$ APB) $\times$ ar( $\Delta$ CDP)=
$\\=(\frac{1}{2}\times BP\times AM).(\frac{1}{2}\times DP \times CN)\\ =\frac{1}{4}\times BP \times DP\times AM\times CN$ ....................(i)

Similarly, ar( $\Delta$ APD) $\times$ ar ( $\Delta$ BPC) =
$=\frac{1}{4}\times BP \times DP\times AM\times CN$ ................(ii)

From eq (i) and eq (ii), we get

$ar (APB) \times ar (CPD) = ar (APD) \times ar (BPC).$
Hence proved.

Q7 (i) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

$\small ar(PRQ)=\frac{1}{2}ar(ARC)$

Answer:

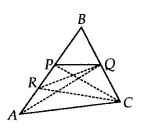
We have $\Delta$ ABC such that P, Q and R are the midpoints of the side AB, BC and AP respectively. Join PQ, QR, AQ, PC and RC as shown in the figure.
Now, in $\Delta$ APC,
Since R is the midpoint. So, RC is the median of the $\Delta$ APC
Therefore, ar( $\Delta$ ARC) = 1/2 . ar ( $\Delta$ APC)............(i)

Also, in $\Delta$ ABC, P is the midpoint. Thus CP is the median.
Therefore, ar( $\Delta$ APC) = 1/2. ar ( $\Delta$ ABC)............(ii)

Also, AQ is the median of $\Delta$ ABC
Therefore, 1/2. ar ( $\Delta$ ABC) = ar (ABQ)............(iii)

In $\Delta$ APQ, RQ is the median.
Therefore, ar ( $\Delta$ PRQ) = 1/2 .ar ( $\Delta$ APQ).............(iv)

In $\Delta$ ABQ, PQ is the median
Therefore, ar( $\Delta$ APQ) = 1/2. ar( $\Delta$ ABQ).........(v)

From eq (i),
$\frac{1}{2}ar(\Delta ARC)= \frac{1}{4}ar(\Delta APC)$ ...........(vi)
Now, put the value of ar( $\Delta$ APC) from eq (ii), we get
Taking RHS;
$= \frac{1}{8}[ar(\Delta ABC)]$
$= \frac{1}{4}[ar(\Delta ABQ)]$ (from equation (iii))

$= \frac{1}{2}[ar(\Delta APQ)]$ (from equation (v))

$=ar(\Delta PRQ)$ (from equation (iv))

$\Rightarrow$ $\small ar(PRQ)=\frac{1}{2}ar(ARC)$

Hence proved.

Q7 (ii) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
$\small ar(RQC)=\frac{3}{8}ar(ABC)$

Answer:

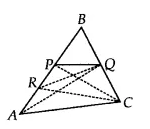
In $\Delta$ RBC, RQ is the median
Therefore ar( $\Delta$ RQC) = ar( $\Delta$ RBQ)
= ar (PRQ) + ar (BPQ)
= 1/8 (ar $\Delta$ ABC) + ar( $\Delta$ BPQ) [from eq (vi) & eq (A) in part (i)]
= 1/8 (ar $\Delta$ ABC) + 1/2 (ar $\Delta$ PBC) [ since PQ is the median of $\Delta$ BPC]
= 1/8 (ar $\Delta$ ABC) + (1/2).(1/2)(ar $\Delta$ ABC) [CP is the medain of $\Delta$ ABC]
= 3/8 (ar $\Delta$ ABC)

Hence proved.

Q7 (iii) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

$ar (PBQ) = ar (ARC)$

Answer:

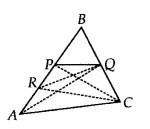
QP is the median of $\Delta$ ABQ
Therefore, ar( $\Delta$ PBQ) = 1/2. (ar $\Delta$ ABQ)

= (1/2). (1/2) (ar $\Delta$ ABC) [since AQ is the median of $\Delta$ ABC
= 1/4 (ar $\Delta$ ABC)
= ar ( $\Delta$ ARC) [from eq (A) of part (i)]

Hence proved.

Q8 (i) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small \Delta MBC\cong \Delta ABD$

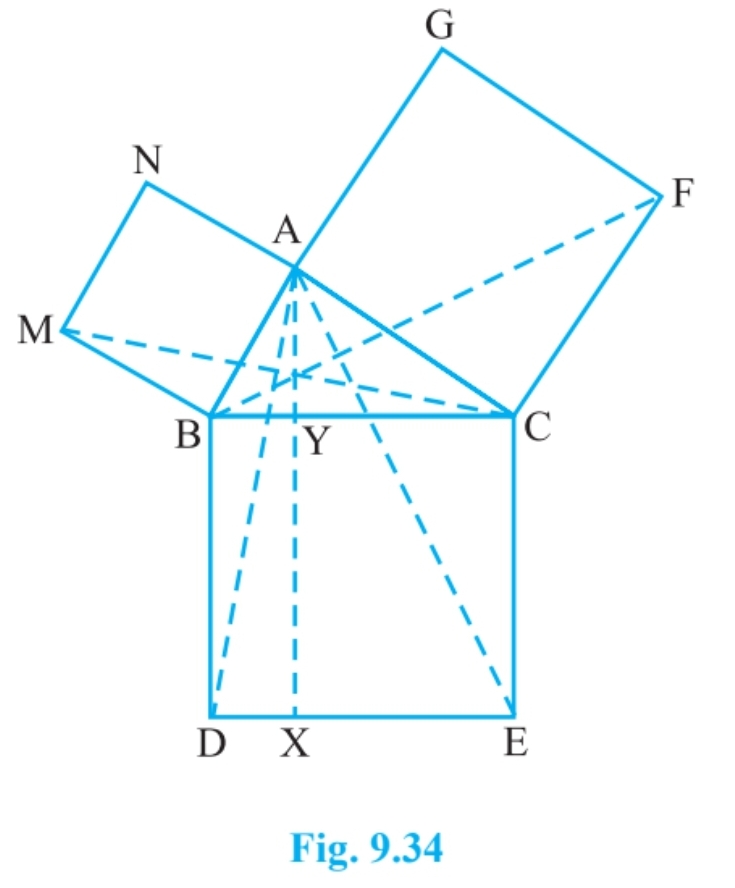
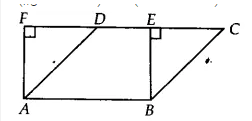
Answer:

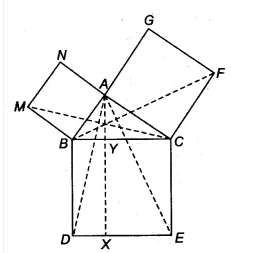
We have, a $\Delta$ ABC such that BCED, ACFG and ABMN are squares on its side BC, CA and AB respec. Line segment $\small AX\perp DE$ meets BC at Y

(i) $\angle CBD = \angle MBA$ [each 90]
Adding $\angle ABC$ on both sides, we get
$\angle ABC + \angle CBD = \angle MBA + \angle ABC$
$\Rightarrow \angle ABD = \angle MBC$
In $\Delta$ ABD and $\Delta$ MBC, we have
AB = MB
BD = BC
$\angle ABD = \angle MBC$
Therefore, By SAS congruency
$\Delta$ ABD $\cong$ $\Delta$ MBC

Hence proved.

Q8 (ii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(BYXD)=2ar(MBC)$

Answer:

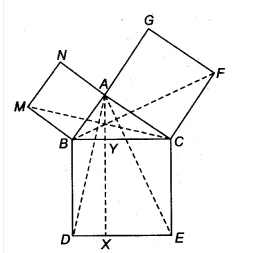
SInce ||gm BYXD and $\Delta$ ABD are on the same base BD and between same parallels BD and AX
Therefore, ar( $\Delta$ ABD) = 1/2. ar(||gm BYXD)..........(i)

But, $\Delta$ ABD $\cong$ $\Delta$ MBC (proved in 1st part)
Since congruent triangles have equal areas.
Therefore, By using equation (i) we get
$\small ar(BYXD)=2ar(MBC)$
Hence proved.

Q8 (iii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $ar(BYXD)=ar(ABMN)$

Answer:

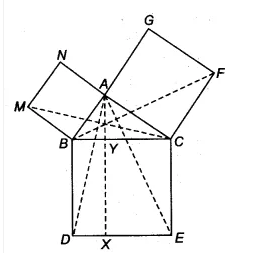
Since, ar (||gm BYXD) = 2 .ar ( $\Delta$ MBC) ..........(i) [already proved in 2nd part]
and, ar (sq. ABMN) = 2. ar ( $\Delta$ MBC)............(ii)
[Since ABMN and AMBC are on the same base MB and between same parallels MB and NC]
From eq(i) and eq (ii), we get

$\small ar(BYXD)=ar(ABMN)$

Q8 (iv) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small \Delta FCB\cong \Delta ACE$

Answer:

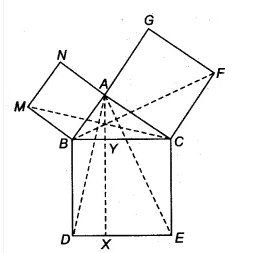
$\angle FCA = \angle BCE$ [both 90]
By adding $\angle$ ABC on both sides we get
$\angle$ ABC + $\angle$ FCA = $\angle$ ABC + $\angle$ BCE
$\angle$ FCB = $\angle$ ACE

In $\Delta$ FCB and $\Delta$ ACE
FC = AC [sides of square]
BC = AC [sides of square]
$\angle$ FCB = $\angle$ ACE
$\Rightarrow$$\Delta$ FCB $\cong$ $\Delta$ ACE

Hence proved.

Q8 (v) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(CYXE)=2ar(FCB)$

Answer:

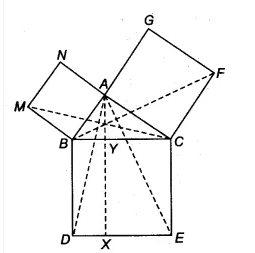
Since ||gm CYXE and $\Delta$ ACE lie on the same base CE and between the same parallels CE and AX.
Therefore, 2. ar( $\Delta$ ACE) = ar (||gm CYXE)
B ut, $\Delta$ FCB $\cong$ $\Delta$ ACE (in iv part)
Since the congruent triangle has equal areas. So,
$\small ar(CYXE)=2ar(FCB)$
Hence proved.

Q8 (vi) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(CYXE)=ar(ACFG)$

Answer:

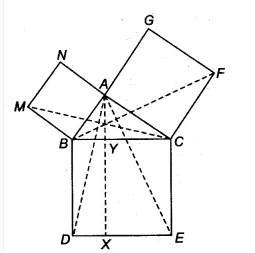
Since ar( ||gm CYXE) = 2. ar( $\Delta$ ACE) {in part (v)}...................(i)
Also, $\Delta$ FCB and quadrilateral ACFG lie on the same base FC and between the same parallels FC and BG.
Therefore, ar (quad. ACFG) = 2.ar( $\Delta$ FCB ) ................(ii)

From eq (i) and eq (ii), we get

$\small ar(CYXE)=ar(ACFG)$
Hence proved.

Q8 (vii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(BCED)=ar(ABMN)+ar(ACFG)$

Answer:

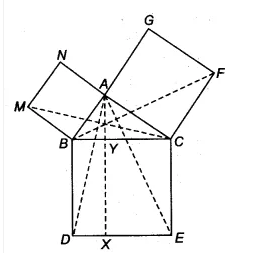
We have,
ar(quad. BCDE) = ar(quad, CYXE) + ar(quad. BYXD)

= ar(quad, CYXE) + ar (quad. ABMN) [already proved in part (iii)]
Thus, $\small ar(BCED)=ar(ABMN)+ar(ACFG)$

Hence proved.