NCERT Solutions for Exercise 9.1 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles

Edited By Safeer PP | Updated on Jul 18, 2022 03:13 PM IST

NCERT Solutions for Class 9 Maths exercise 9.1 - The properties of parallelograms on the same base and between the same parallels are identified in NCERT solutions for Class 9 Maths chapter 9 exercise 9.1. It includes questions about the diagonal of a parallelogram, its base, side lengths, area, and other unique properties of parallelograms. More such properties of this geometric shape are addressed in this NCERT exercise. Class 9 Maths chapter 9 exercise 9.1 two shapes are stated to be on the common base and between the same parallels if: A side is common between two shapes. The vertices opposite the same side and the sides parallel to the common base are both on the same straight line parallel to the base.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.1
More About NCERT Solutions for Class 9 Maths Exercise 9.1
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions

If two shapes are congruent then the amount of area occupied by them will also be equal but the vice-versa of this statement is not true i.e. two figures having the same area need not be congruent.

A parallelogram is a geometrical shape with sides that are parallel to each other in two dimensions. It's a four-sided polygon (also known as a quadrilateral) with two parallel sides that are the same length. A parallelogram's interior opposite angles are also equal. The sum of a parallelogram's adjacent angles is 180 degrees.

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.1

Q Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

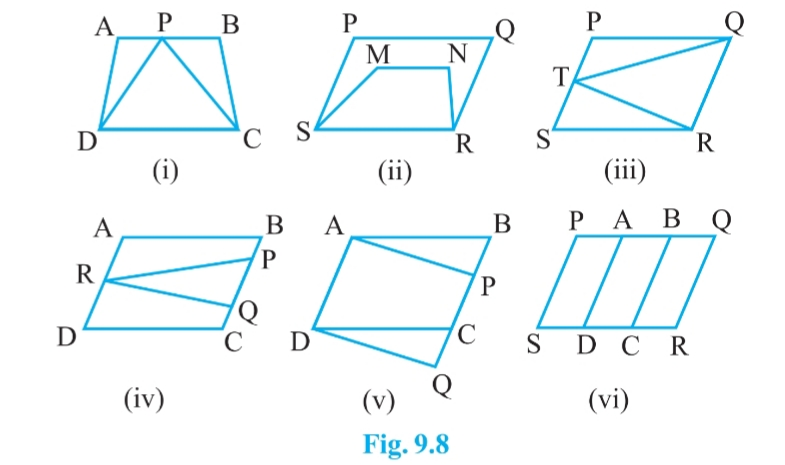
1640236058747

Answer:

In figure (i), (iii) and (v) we can see that. they lie on the same base and between the same parallel lines.
In figure (i) figure (iii) figure (v)
Common base DC QR AD
Two parallels DC and AB QR and PS AD and BQ

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What is the main concept of NCERT solutions for Class 9 Maths exercise 9.1?

In this exercise, we learn about dealings with areas related to triangles and parallelograms especially if they are on the common base and between the same parallels.

2. If two figures A and B are congruent then what is the relation between their areas?

If figure A and figure B are congruent to each other then:

Area of (A) = Area of (B)

3. What do you understand by area of a given surface?

The area of a given surface is defined as the space occupied by the surface.

4. What is the area of a square?

The area of a given surface is defined as the space occupied by the surface.

5. What do you mean by figures on the same base?

Two figures are said to be on the same base if they both have one common side as their base.

6. What do you understand by figures on the same base and between the same parallels?

Two figures are supposed to be on the same base and between the same parallels in the event that the two of them have one common side as their base and the vertices which are inverse(opposite) to the normal base lie on both lie in a parallel line.

7. Fund the area of a rectangle with sides 6cm and 5cm?

8. Can we consider rectangle as a parallelogram?

Yes, we can consider a rectangle as a parallelogram as both of its opposite sides are parallel to each other.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

AMU Class 1 Admission 2025: Application Process, Eligibility & Key Dates

Dec 30, 2024

Jamia Millia Islamia School Admission 2025: Application Process, Eligibility & Dates

Dec 30, 2024

SoSE Delhi School Admission 2025: All You Need to Know About Eligibility, Dates & Process

Dec 30, 2024

DBSE Result 2025, Check Delhi Board 10th, 12th Result

Dec 30, 2024

NMMS Chhattisgarh Result 2024-25: Check Merit List, Cut Off Marks

Dec 28, 2024

CBSE Scholarship 2024-25: Check CBSE Scholarships for Class 10, 12

Dec 27, 2024

HOS 12th Date Sheet 2025 - Haryana Open School Class 12 Exam Schedule

Dec 27, 2024

AMU School Admission 2025 - Know Application Process, Eligibility & Important Dates

Dec 27, 2024

Upcoming School Exams

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

National Institute of Open Schooling 10th examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Admit Card

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Exam Pattern

Answer Key

Result

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is