NCERT Solutions for Exercise 9.2 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.2

Q1 In Fig. $9.15$ , ABCD is a parallelogram, $AE\perp DC$ and $CF\perp AD$ . If $AB=16cm$ , $AE=8cm$ and $CF=10cm$ , find AD.

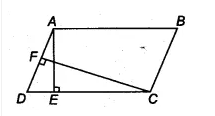
Answer:

We have,
AE $\perp$ DC and CF $\perp$ AD
AB = 16 cm, AE = 8 cm and CF = 10 cm

Since ABCD is a parallelogram,
therefore, AB = DC = 16 cm
We know that, area of parallelogram (ABCD) = base . height
= CD $\times$ AE = (16 $\times$ 8 ) $c{m}^2$
SInce, CF $\perp$ AD
therefore area of parallelogram = AD $\times$ CF = 128 $c{m}^2$
= AD = 128/10
= AD = 12.8 cm

Thus the required length of AD is 12.8 cm.

Q2 If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that

$ar(EFGH)=\frac{1}{2}ar(ABCD)$

Answer:

Join GE and HE,
Since F, F, G, H are the mid-points of the parallelogram ABCD. Therefore, GE || BC ||AD and HF || DC || AB.
It is known that if a triangle and the parallelogram are on the same base and between the same parallel lines. then the area of the triangle is equal to the half of the area of the parallelogram.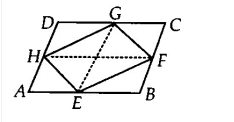

Now, $\mathrm{\Delta }$ EFG and ||gm BEGC are on the same base and between the same parallels EG and BC.
Therefore, ar ( $\mathrm{\Delta }$ EFG) = $1/2$ ar (||gm BEGC)...............(i)
Similarly, ar ( $\mathrm{\Delta }$ EHG) = 1/2 . ar(||gm AEGD)..................(ii)
By adding eq (i) and eq (ii), we get

ar ( $\mathrm{\Delta }$ EFG) + ar ( $\mathrm{\Delta }$ EHG) = 1/2 (ar (||gm BEGC) + ar(||gm AEGD))
ar (EFGH) = 1/2 ar(ABCD)
Hence proved

Q3 P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that $ar(APB)=ar(BCQ)$ .

Answer:

We have,
ABCD is a parallelogram, therefore AB || CD and BC || AD.

Now, $\mathrm{\Delta }$ APB and ||gm ABCD are on the same base AB and between two parallels AB and DC.
Therefore, ar ( $\mathrm{\Delta }$ APB) = 1/2 . ar(||gm ABCD)...........(i)

Also, $\mathrm{\Delta }$ BQC and ||gm ABCD are on the same base BC and between two parallels BC and AD.
Therefore, ar( $\mathrm{\Delta }$ BQC) = 1/2 . ar(||gmABCD)...........(ii)

From eq(i) and eq (ii), we get,
ar ( $\mathrm{\Delta }$ APB) = ar( $\mathrm{\Delta }$ BQC)
Hence proved.

Q4 (i) In Fig. $9.16$ , P is a point in the interior of a parallelogram ABCD. Show that
$ar(APB)+ar(PCD)=\frac{1}{2}ar(ABCD)$

[ Hint : Through P, draw a line parallel to AB.]

Answer:

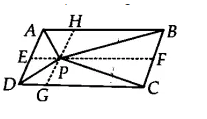
We have a ||gm ABCD and AB || CD, AD || BC. Through P, draw a line parallel to AB
Now, $\mathrm{\Delta }$ APB and ||gm ABEFare on the same base AB and between the same parallels EF and AB.
Therefore, ar ( $\mathrm{\Delta }$ APB) = 1/2 . ar(ABEF)...............(i)
Similarly, ar ( $\mathrm{\Delta }$ PCD ) = 1/2 . ar (EFDC) ..............(ii)
Now, by adding both equations, we get
$ar(APB)+ar(PCD)=\frac{1}{2}ar(ABCD)$

Hence proved.

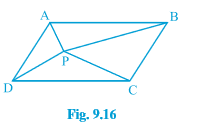
Q4 (ii) In Fig. $9.16$ , P is a point in the interior of a parallelogram ABCD. Show that

$ar(APD)+ar(PBC)=ar(APB)+ar(PCD)$

[ Hint: Through P, draw a line parallel to AB.]

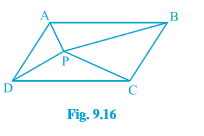
Answer:

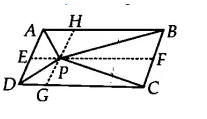
We have a ||gm ABCD and AB || CD, AD || BC. Through P, draw a line parallel to AB
Now, $\mathrm{\Delta }$ APD and ||gm ADGHare on the same base AD and between the same parallels GH and AD.
Therefore, ar ( $\mathrm{\Delta }$ APD) = 1/2 . ar(||gm ADGH).............(i)

Similarily, ar ( $\mathrm{\Delta }$ PBC) = 1/2 . ar(||gm BCGH)............(ii)

By adding the equation i and eq (ii), we get

$ar(APD)+ar(PBC)=ar(APB)+ar(PCD)$

Hence proved.

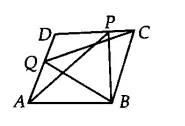
Q5 In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that

(i) $ar(PQRS)=ar(ABRS)$
(ii) $ar(AXS)=\frac{1}{2}ar(PQRS)$

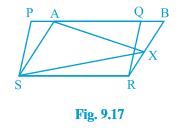Answer:

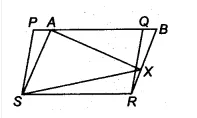
(i) Parallelogram PQRS and ABRS are on the same base RS and between the same parallels RS and PB.
Therefore, $ar(PQRS)=ar(ABRS)$ ............(i)
Hence proved

(ii) $\mathrm{\Delta }$ AXS and ||gm ABRS are on the same base AS and between same parallels AS and RB.
Therefore, ar ( $\mathrm{\Delta }$ AXS) = 1/2 . ar(||gm ABRS)............(ii)

Now, from equation (i) and equation (ii), we get

$ar(AXS)=\frac{1}{2}ar(PQRS)$

Hence proved.

Q6 A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

Answer:

We have a field in the form of parallelogram PQRS and a point A is on the side RS. Join AP and AQ. The field is divided into three parts i.e, $\mathrm{\Delta }$ APS, $\mathrm{\Delta }$ QAR and $\mathrm{\De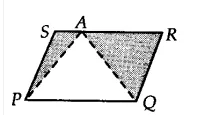lta }$ PAQ.

Since $\mathrm{\Delta }$ APQ and parallelogram, PQRS is on the same base PQ and between same parallels RS and PQ.
Therefore, $ar(\mathrm{\Delta }APQ)=\frac{1}{2}ar(PQRS)$ ............(i)
We can write above equation as,

ar (||gm PQRS) - [ar ( $\mathrm{\Delta }$ APS) + ar( $\mathrm{\Delta }$ QAR)] = 1/2 .ar(PQRS)
$\Rightarrow ar(\mathrm{\Delta }APS)+ar(\mathrm{\Delta }QAR)=\frac{1}{2}ar(PQRS)$
from equation (i),
$\Rightarrow ar(\mathrm{\Delta }APS)+ar(\mathrm{\Delta }QAR)=ar(\mathrm{\Delta }APQ)$

Hence, she can sow wheat in $\mathrm{\Delta }$ APQ and pulses in [ $\mathrm{\Delta }$ APS + $\mathrm{\Delta }$ QAR] or wheat in [ $\mathrm{\Delta }$ APS + $\mathrm{\Delta }$ QAR] and pulses in $\mathrm{\Delta }$ APQ.