NCERT Solutions for Exercise 9.4 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles

Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with

Plan, Prepare & Make the Best Career Choices

NCERT Solutions for Exercise 9.4 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles

Edited By Safeer PP | Updated on Jul 29, 2022 06:22 PM IST

The NCERT Solutions for Class 9 Maths exercise 9.4 is an optional (not from the examination point of view) exercise which comprises of theorems related to the previous exercises which include concepts of parallelograms and triangle on the same base and between the same parallels, having questions related to areas of figure which includes the medians for triangles.

This Story also Contains

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.1
More About NCERT Solutions for Class 9 Maths Exercise 9.4
Benefits of NCERT Solutions for Class 9 Maths Exercise 9.4
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions

Few important concepts related to NCERT syllabus Class 9 Maths chapter 9 exercise 9.4 in order to solve this exercise are:

Parallelograms having the same base and are in between the same parallels have the same area, as because the height (distance between the two parallel lines) continues as before for the two parallelograms and they have same bases subsequently their regions are equivalent.
Triangle that has a same base or the equivalent base and are between same pair of parallel lines have equivalent area. This is on the grounds that we realize that the area of the triangle is a half of the result of base and height. Since the height (distance between the parallels) continues as before for the two triangles and they have same bases subsequently their area are equivalent.

Major questions in this exercise use a blend of at least two or more concepts.

Along with NCERT book Class 9 Maths chapter 9 exercise 9.4 the following exercises are also present.

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.1

Q1 Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Answer:

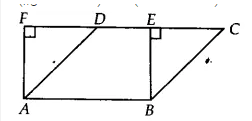
1595870426562

We have ||gm ABCD and a rectangle ABEF both lie on the same base AB such that, ar(||gm ABCD) = ar(ABEF)
for rectangle, AB = EF
and for ||gm AB = CD
$\Rightarrow$ CD = EF
$\Rightarrow$ AB + CD = AB + EF ...........(i)

SInce $\Delta$ BEC and $\Delta$ AFD are right angled triangle
Therefore, AD > AF and BC > BE
$\Rightarrow$ (BC + AD ) > (AF + BE)...........(ii)

Adding equation (i) and (ii), we get

(AB + CD)+(BC + AD) > (AB + BE) + (AF + BE)
$\Rightarrow$ (AB + BC + CD + DA) > (AB + BE + EF + FA)
Hence proved, perimeter of ||gm ABCD is greater than perimeter of rectangle ABEF.

Q2 In Fig. $\small 9.30$ , D and E are two points on BC such that $\small BD=DE=EC$ . Show that $\small ar(ABD)=ar(ADE)=ar(AEC)$ .

1640236583768 Answer:

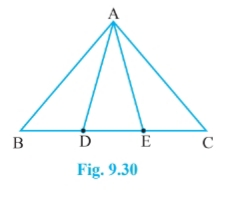
In $\Delta$ ABC, D and E are two points on BC such that BD = DE = EC

AD is the median of ABE, therefore,

area of ABD= area of AED...................(1)

AE is the median of ACD, therefore,

area of AEC= area of AED...................(2)

From (1) and (2)

area of ABD=area of AED= area of AEC
Hence proved.

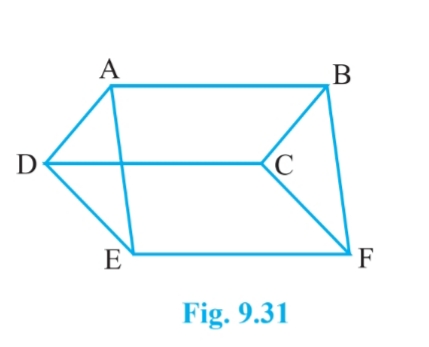
Q3 In Fig. $\small 9.31$ , ABCD, DCFE and ABFE are parallelograms. Show that $\small ar(ADE)=ar(BCF)$ .

1640236638372 Answer:

Given,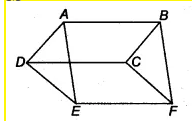
1595870559171
ABCD is a parallelogram. Therefore, AB = CD & AD = BC & AB || CD .......(i)

Now, $\Delta$ ADE and $\Delta$ BCF are on the same base AD = BC and between same parallels AB and EF.
Therefore, ar ( $\Delta$ ADE) = ar( $\Delta$ BCF)

Hence proved.

Q4 In Fig. $\small 9.32$ , ABCD is a parallelogram and BC is produced to a point Q such that $\small AD=CQ$ . If AQ intersects DC at P, show that $\small ar (BPC) = ar (DPQ)$ . [ Hint : Join AC.]

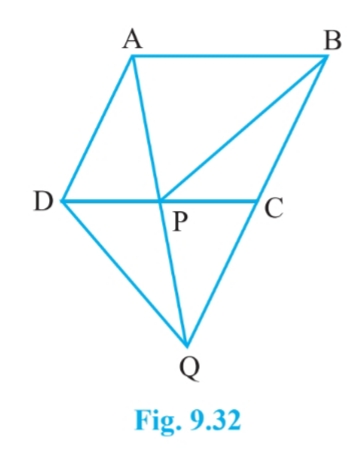1640236665039 Answer:

1595870619379
Given,
ABCD is a ||gm and AD = CQ. Join AC.
Since $\Delta$ DQC and $\Delta$ ACD lie on the same base QC and between same parallels AD and QC.
Therefore, ar( $\Delta$ DQC) = ar( $\Delta$ ACD).......(i)

Subtracting ar( $\Delta$ PQC) from both sides in eq (i), we get
ar( $\Delta$ DPQ) = ar( $\Delta$ PAC).............(i)

Since $\Delta$ PAC and $\Delta$ PBC are on the same base PC and between same parallel PC and AB.
Therefore, ar( $\Delta$ PAC) = ar( $\Delta$ PBC)..............(iii)

From equation (ii) and eq (ii), we get

$\small ar (BPC) = ar (DPQ)$

Hence proved.

Q5 (i) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

$\small ar(BDE)=\frac{1}{4}ar(ABC)$

[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

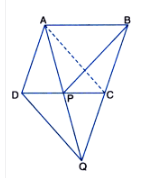
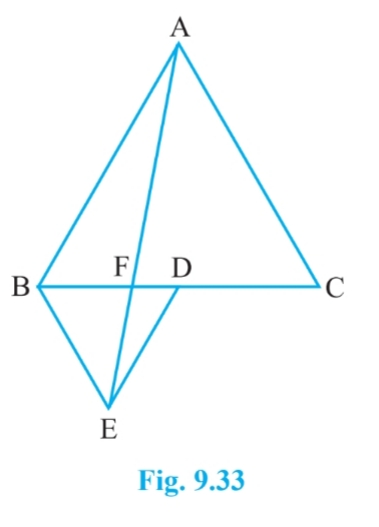1640236707923 Answer:

1595870673567
Let join the CE and AD and draw $EP \perp BC$ . It is given that $\Delta$ ABC and $\Delta$ BDE is an equilateral triangle.
So, AB =BC = CA = $a$ and D i sthe midpoint of BC
therefore, $BD = \frac{a}{2}= DE = BE$
(i) Area of $\Delta$ ABC = $\frac{\sqrt{3}}{4}a^2$ and
Area of $\Delta$ BDE = $\frac{\sqrt{3}}{4}(\frac{a}{2})^2= \frac{\sqrt{3}}{16}a^2$

Hence, $\small ar(BDE)=\frac{1}{4}ar(ABC)$

Q5 (ii) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BDE)=\frac{1}{2}ar(BAE)$

[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

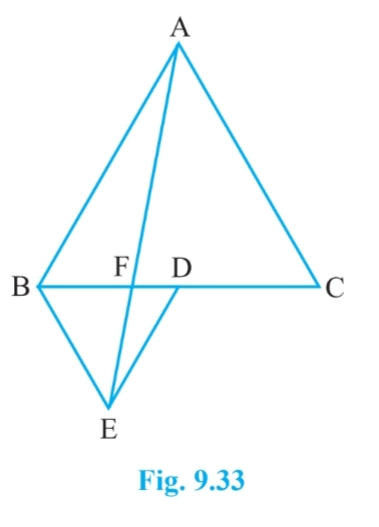
1640236728299

Answer:

1595870700069
Since $\Delta$ ABC and $\Delta$ BDE are equilateral triangles.
Therefore, $\angle$ ACB = $\angle$ DBE = $60^0$
$\Rightarrow$ BE || AC

$\Delta$ BAE and $\Delta$ BEC are on the same base BE and between same parallels BE and AC.
Therefore, ar ( $\Delta$ BAE) = ar( $\Delta$ BEC)
$\Rightarrow$ ar( $\Delta$ BAE) = 2 ar( $\Delta$ BED) [since D is the meian of $\Delta$ BEC ]
$\Rightarrow$ $\small ar(BDE)=\frac{1}{2}ar(BAE)$
Hence proved.

Q5 (iii) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(ABC)=2ar(BEC)$

[ Hint : Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

1640236744718

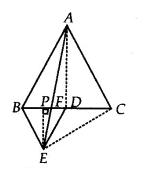
Answer:

We already proved that,
ar( $\Delta$ ABC) = 4.ar( $\Delta$ BDE) (in part 1)
and, ar( $\Delta$ BEC) = 2. ar( $\Delta$ BDE) (in part ii )

$\Rightarrow$ ar( $\Delta$ ABC) = 2. ar( $\Delta$ BEC)

Hence proved.

Q5 (iv) In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BFE)=ar(AFD)$
[ Hint: Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

1640236764354

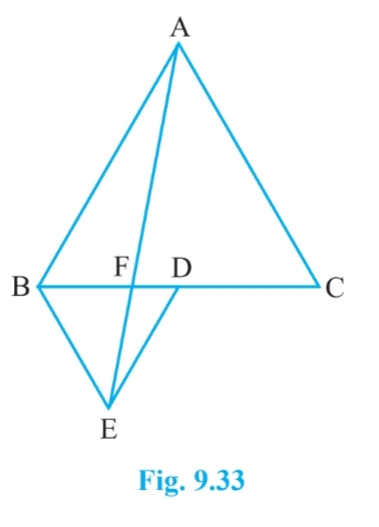
Answer:

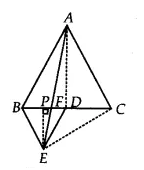
1595870707470
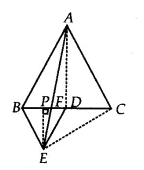
Since $\Delta$ ABC and $\Delta$ BDE are equilateral triangles.
Therefore, $\angle$ ACB = $\angle$ DBE = $60^0$
$\Rightarrow$ BE || AC

$\Delta$ BDE and $\Delta$ AED are on the same base ED and between same parallels AB and DE.
Therefore, ar( $\Delta$ BED) = ar( $\Delta$ AED)

On subtracting $\Delta$ EFD from both sides we get

$\small ar(BFE)=ar(AFD)$

Hence proved.

Q5 (v) In Fig. $\small 9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$\small ar(BFE)=2ar(FED)$

[ Hint : Join EC and AD. Show that $\small BE\parallel AC$ and $\small DE\parallel AB$ , etc.]

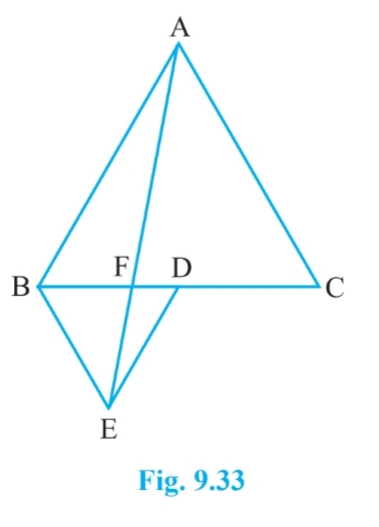
1640236770366

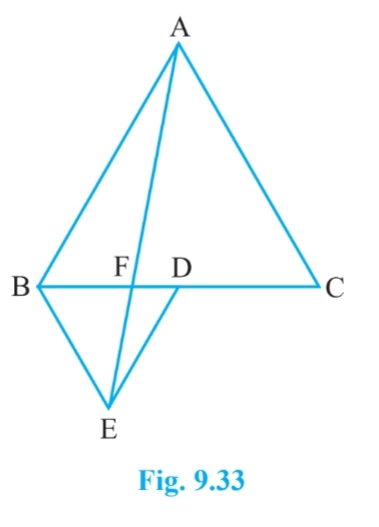
Answer:

1595870716157
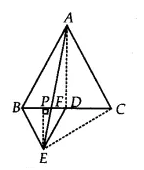
In right angled triangle $\Delta$ ABD, we get

$\\AB^2 = AD^2+BD^2\\ AD^2 = AB^2-BD^2$
$=a^2 - \frac{a^2}{4}=\frac{3a^2}{4}$
$AD=\frac{\sqrt{3}a}{2}$

So, in $\Delta$ PED,
$PE^2 = DE^2-DP^2$
$\\=(\frac{a}{2})^2-(\frac{a}{4})^2\\ =\frac{3a^2}{16}$
So, $PE=\frac{\sqrt{3}a}{4}$

Therefore, the Area of $\Delta AFD =1/2 (FD)\frac{\sqrt{3}a}{2}$ ..........(i)

And, Area of triangle $\Delta EFD =1/2 (FD)\frac{\sqrt{3}a}{4}$ ...........(ii)

From eq (i) and eq (ii), we get
ar( $\Delta$ AFD) = 2. ar( $\Delta$ EFD)
Since ar( $\Delta$ AFD) = ar( $\Delta$ BEF)

$\Rightarrow$ $\small ar(BFE)=2ar(FED)$

Q5 (vi) In Fig. $9.33$ , ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
$ar (FED) = \frac{1}{8} ar (AFC)$

[ Hint: Join EC and AD. Show that $BE\parallel AC$ and $DE\parallel AB$ , etc.]

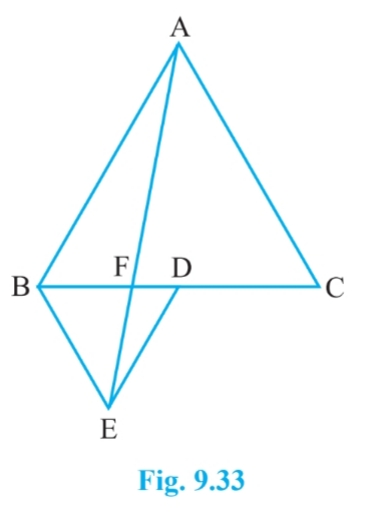1640236806124 Answer:

$ar(\Delta AFC) =$
$\\= ar(\Delta AFD) + ar(\Delta ADC)\\ = ar(\Delta BFE) + 1/2. ar(\Delta ABC)\\ = ar(\Delta BFE) + 1/2\times [4\times ar(\Delta BDE)]\\ = ar(\Delta BFE) + 2\times ar(\Delta BDE)$
$= 2\times ar (\Delta FED) + 2\times [ar(\Delta BFE) + ar(\Delta FED)]$ .....(from part (v) ar( $\Delta$ BFE) = 2. ar( $\Delta$ FED) ]
$\\=2ar(\Delta FED) + 2[3\times ar(\Delta FED)]\\ =8\times ar(\Delta FED)$

$ar (FED) = \frac{1}{8} ar (AFC)$
Hence proved.

Q6 Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that $ar (APB) \times ar (CPD) = ar (APD) \times ar (BPC).$

[ Hint: From A and C, draw perpendiculars to BD.]

Answer:

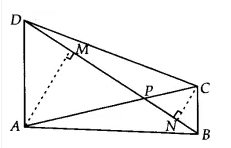
1595870785823
Given that,
A quadrilateral ABCD such that it's diagonal AC and BD intersect at P. Draw $AM \perp BD$ and $CN \perp BD$

Now, ar( $\Delta$ APB) = $\frac{1}{2}\times BP\times AM$ and,
$ar(\Delta CDP)=\frac{1}{2}\times DP\times CN$
Therefore, ar( $\Delta$ APB) $\times$ ar( $\Delta$ CDP)=
$\\=(\frac{1}{2}\times BP\times AM).(\frac{1}{2}\times DP \times CN)\\ =\frac{1}{4}\times BP \times DP\times AM\times CN$ ....................(i)

Similarly, ar( $\Delta$ APD) $\times$ ar ( $\Delta$ BPC) =
$=\frac{1}{4}\times BP \times DP\times AM\times CN$ ................(ii)

From eq (i) and eq (ii), we get

$ar (APB) \times ar (CPD) = ar (APD) \times ar (BPC).$
Hence proved.

Q7 (i) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

$\small ar(PRQ)=\frac{1}{2}ar(ARC)$

Answer:

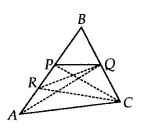
1595870842857
We have $\Delta$ ABC such that P, Q and R are the midpoints of the side AB, BC and AP respectively. Join PQ, QR, AQ, PC and RC as shown in the figure.
Now, in $\Delta$ APC,
Since R is the midpoint. So, RC is the median of the $\Delta$ APC
Therefore, ar( $\Delta$ ARC) = 1/2 . ar ( $\Delta$ APC)............(i)

Also, in $\Delta$ ABC, P is the midpoint. Thus CP is the median.
Therefore, ar( $\Delta$ APC) = 1/2. ar ( $\Delta$ ABC)............(ii)

Also, AQ is the median of $\Delta$ ABC
Therefore, 1/2. ar ( $\Delta$ ABC) = ar (ABQ)............(iii)

In $\Delta$ APQ, RQ is the median.
Therefore, ar ( $\Delta$ PRQ) = 1/2 .ar ( $\Delta$ APQ).............(iv)

In $\Delta$ ABQ, PQ is the median
Therefore, ar( $\Delta$ APQ) = 1/2. ar( $\Delta$ ABQ).........(v)

From eq (i),
$\frac{1}{2}ar(\Delta ARC)= \frac{1}{4}ar(\Delta APC)$ ...........(vi)
Now, put the value of ar( $\Delta$ APC) from eq (ii), we get
Taking RHS;
$= \frac{1}{8}[ar(\Delta ABC)]$
$= \frac{1}{4}[ar(\Delta ABQ)]$ (from equation (iii))

$= \frac{1}{2}[ar(\Delta APQ)]$ (from equation (v))

$=ar(\Delta PRQ)$ (from equation (iv))

$\Rightarrow$ $\small ar(PRQ)=\frac{1}{2}ar(ARC)$

Hence proved.

Q7 (ii) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
$\small ar(RQC)=\frac{3}{8}ar(ABC)$

Answer:

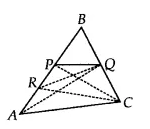
1595870850022
In $\Delta$ RBC, RQ is the median
Therefore ar( $\Delta$ RQC) = ar( $\Delta$ RBQ)
= ar (PRQ) + ar (BPQ)
= 1/8 (ar $\Delta$ ABC) + ar( $\Delta$ BPQ) [from eq (vi) & eq (A) in part (i)]
= 1/8 (ar $\Delta$ ABC) + 1/2 (ar $\Delta$ PBC) [ since PQ is the median of $\Delta$ BPC]
= 1/8 (ar $\Delta$ ABC) + (1/2).(1/2)(ar $\Delta$ ABC) [CP is the medain of $\Delta$ ABC]
= 3/8 (ar $\Delta$ ABC)

Hence proved.

Q7 (iii) P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

$ar (PBQ) = ar (ARC)$

Answer:

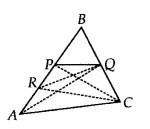
1595870859523

QP is the median of $\Delta$ ABQ
Therefore, ar( $\Delta$ PBQ) = 1/2. (ar $\Delta$ ABQ)

= (1/2). (1/2) (ar $\Delta$ ABC) [since AQ is the median of $\Delta$ ABC
= 1/4 (ar $\Delta$ ABC)
= ar ( $\Delta$ ARC) [from eq (A) of part (i)]

Hence proved.

Q8 (i) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small \Delta MBC\cong \Delta ABD$

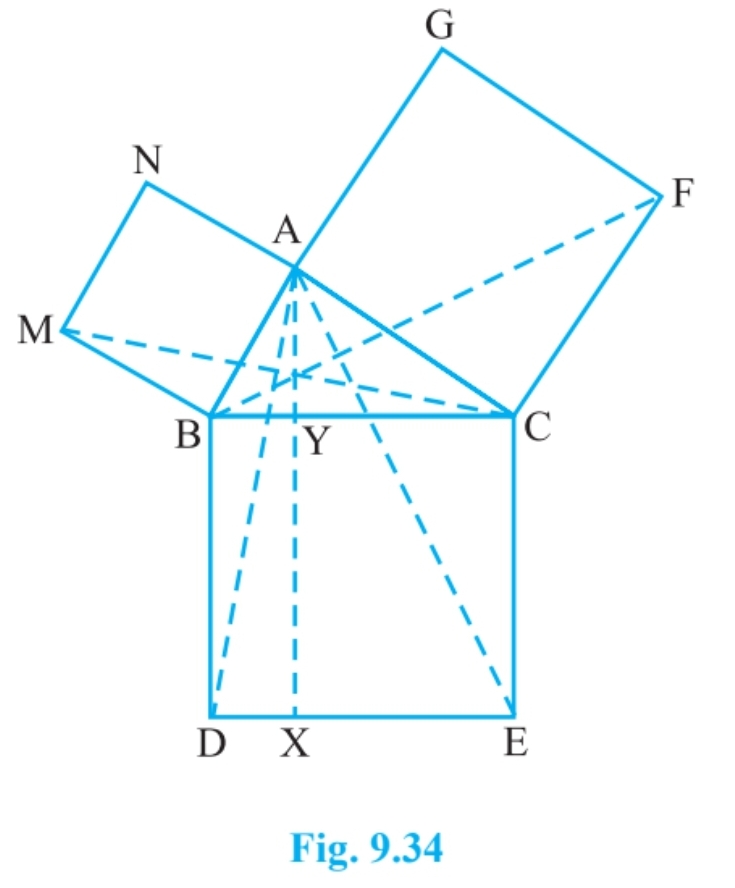
1640236844952

Answer:

1595870953001
We have, a $\Delta$ ABC such that BCED, ACFG and ABMN are squares on its side BC, CA and AB respec. Line segment $\small AX\perp DE$ meets BC at Y

(i) $\angle CBD = \angle MBA$ [each 90]
Adding $\angle ABC$ on both sides, we get
$\angle ABC + \angle CBD = \angle MBA + \angle ABC$
$\Rightarrow \angle ABD = \angle MBC$
In $\Delta$ ABD and $\Delta$ MBC, we have
AB = MB
BD = BC
$\angle ABD = \angle MBC$
Therefore, By SAS congruency
$\Delta$ ABD $\cong$ $\Delta$ MBC

Hence proved.

Q8 (ii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(BYXD)=2ar(MBC)$

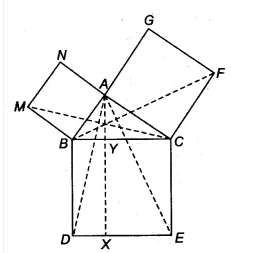
Answer:

1595870964455
SInce ||gm BYXD and $\Delta$ ABD are on the same base BD and between same parallels BD and AX
Therefore, ar( $\Delta$ ABD) = 1/2. ar(||gm BYXD)..........(i)

But, $\Delta$ ABD $\cong$ $\Delta$ MBC (proved in 1st part)
Since congruent triangles have equal areas.
Therefore, By using equation (i) we get
$\small ar(BYXD)=2ar(MBC)$
Hence proved.

Q8 (iii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $ar(BYXD)=ar(ABMN)$

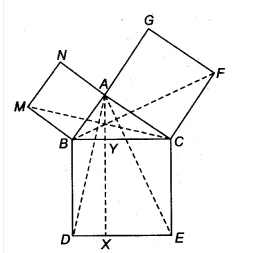
Answer:

1595870972199
Since, ar (||gm BYXD) = 2 .ar ( $\Delta$ MBC) ..........(i) [already proved in 2nd part]
and, ar (sq. ABMN) = 2. ar ( $\Delta$ MBC)............(ii)
[Since ABMN and AMBC are on the same base MB and between same parallels MB and NC]
From eq(i) and eq (ii), we get

$\small ar(BYXD)=ar(ABMN)$

Q8 (iv) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small \Delta FCB\cong \Delta ACE$

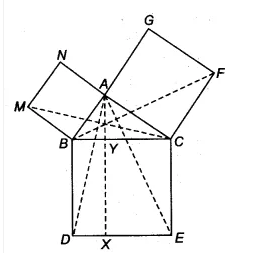
Answer:

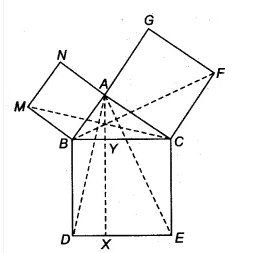
1595870980947
$\angle FCA = \angle BCE$ [both 90]
By adding $\angle$ ABC on both sides we get
$\angle$ ABC + $\angle$ FCA = $\angle$ ABC + $\angle$ BCE
$\angle$ FCB = $\angle$ ACE

In $\Delta$ FCB and $\Delta$ ACE
FC = AC [sides of square]
BC = AC [sides of square]
$\angle$ FCB = $\angle$ ACE
$\Rightarrow$ $\Delta$ FCB $\cong$ $\Delta$ ACE

Hence proved.

Q8 (v) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(CYXE)=2ar(FCB)$

Answer:

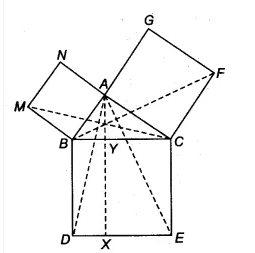
1595870988524
Since ||gm CYXE and $\Delta$ ACE lie on the same base CE and between the same parallels CE and AX.
Therefore, 2. ar( $\Delta$ ACE) = ar (||gm CYXE)
B ut, $\Delta$ FCB $\cong$ $\Delta$ ACE (in iv part)
Since the congruent triangle has equal areas. So,
$\small ar(CYXE)=2ar(FCB)$
Hence proved.

Q8 (vi) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(CYXE)=ar(ACFG)$

Answer:

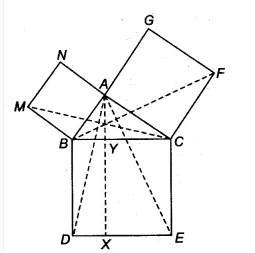
1595871000670
Since ar( ||gm CYXE) = 2. ar( $\Delta$ ACE) {in part (v)}...................(i)
Also, $\Delta$ FCB and quadrilateral ACFG lie on the same base FC and between the same parallels FC and BG.
Therefore, ar (quad. ACFG) = 2.ar( $\Delta$ FCB ) ................(ii)

From eq (i) and eq (ii), we get

$\small ar(CYXE)=ar(ACFG)$
Hence proved.

Q8 (vii) In Fig. $\small 9.34$ , ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $\small AX\perp DE$ meets BC at Y. Show that: $\small ar(BCED)=ar(ABMN)+ar(ACFG)$

Answer:

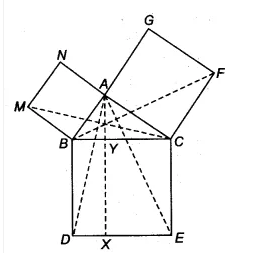
1595871008289
We have,
ar(quad. BCDE) = ar(quad, CYXE) + ar(quad. BYXD)

= ar(quad, CYXE) + ar (quad. ABMN) [already proved in part (iii)]
Thus, $\small ar(BCED)=ar(ABMN)+ar(ACFG)$

Hence proved.

Benefits of NCERT Solutions for Class 9 Maths Exercise 9.4

Exercise 9.4 Class 9 Maths, is based on AREAS OF PARALLELOGRAMS AND TRIANGLES and most of its crucial properties.
From Class 9 Maths chapter 9 exercise 9.4 we get to revise the entire concepts of this chapter in a single exercise.
Understanding the concepts from Class 9 Maths chapter 9 exercise 9.4 will make the concepts and questions from higher standards (like Class10) easier for us.

Also, See

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What is the total fundamental concept of NCERT solutions for Class 9 Maths exercise 9.4?

This exercise deals with all the difficult questions regarding the area of triangles and parallelograms and their properties.

2. If two figures A and B are congruent to each other then what can you describe between the relation of their areas?

If figure A and figure B are congruent to each other then the relation between their areas is that they are equal to each other.

Area of (A) = Area of (B)

3. What do you mean by the term “two figures lies on the same base”?

The term “two figures on the same base” means that two figures which are said to be on the same base have one common side as their base or their commo side (base length) is equal to one other.

4. Find the area of a triangle with base as 6cm and height as 4cm?

The term “two figures on the same base” means that two figures which are said to be on the same base have one common side as their base or their commo side (base length) is equal to one other.

5. Can we consider rectangle and a square both as a parallelogram?

Yes, we can consider a rectangle and a square as a parallelogram as both of its opposite sides are parallel to each other.

6. Find the area of a parallelogram with base as 12cm and height as 10cm?

Yes, we can consider a rectangle and a square as a parallelogram as both of its opposite sides are parallel to each other.

7. Name the different types of parallelograms?

The different types of parallelograms are:

Square
Rectangle
Rhombus and
Parallelogram

8. What do you mean by figures on a similar base and between same parallels ?

Two figures are supposed to be on a same base and between same parallels if the two of them have one common (normal) side as their base and the vertices which are inverse to the normal base lie on a line parallel to the base.

Also Read

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.1 Number Systems

NCERT Solutions for Exercise 14.3 Class 9 Maths Chapter 14 - Statistics

NCERT Solutions for Exercise 13.8 Class 9 Maths Chapter 13 - Surface Area and Volumes

NCERT Solutions for Exercise 13.7 Class 9 Maths Chapter 13 - Surface Area and Volumes

NCERT Solutions for Exercise 13.6 Class 9 Maths Chapter 13 - Surface Area and Volumes

NCERT Books for Class 9 2023 for All Subjects (Maths, Science, Social Science, Hindi English)

NCERT Books for Class 9 Hindi 2023 - Download PDF

NCERT Books for Class 9 Maths 2023-24 - Download PDF

NCERT Books for Class 9 Social Science 2023 - Download PDF

NCERT Books for Class 9 Science 2023-24 - Download PDF (All Chapters)

NCERT Books for Class 9 English 2023-24 (All Chapters) - Download Pdf here!

NCERT Syllabus for Class 9 Science 2023 (Chapter Wise) - Download Pdf

NCERT Syllabus for Class 9 Hindi 2023 - Download PDF Here

NCERT Syllabus for Class 9 (All subjects) 2023 - Download Pdf

NCERT Syllabus for Class 9 Social Science 2023- Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Atoms and Molecules Class 9th Notes - Free NCERT Class 9 Science Chapter 3 Notes - Download PDF

Sound Class 9th Notes - Free NCERT Class 9 Science Chapter 12 Notes - Download PDF

Quadrilaterals Class 9th Notes - Free NCERT Class 9 Maths Chapter 8 Notes - Download PDF

Improvement In Food Resources Class 9 Notes-Free NCERT Class 9 Science Chapter 15 Notes- Download PDF

Why Do We Fall ill Class 9th Notes-Free NCERT Class 9 Science Chapter 13 Notes-Download PDF-Why Do We Fall ill-Class 9 Notes

Work and Energy Class 9th Notes - Free NCERT Class 9 Science Chapter 11 Notes - Download PDF

Articles

10th Time Table 2024 - Download All Boards Class 10th Date Sheet Here

Nov 28, 2023

ITI Courses After 12th - Course Duration & Top Institutes

Nov 16, 2023

UP Madarsa Board Result 2024 for Molvi, Munshi, Alim, Kamil & Fazil - UPBME Result Here

Nov 15, 2023

Diwali Essay: About Deepavali, Short Paragraphs, 10 Lines On Diwali

Nov 09, 2023

Class 10 Sample Papers - Download UP Board, CBSE, HBSE, All Boards Class 10 Sample Papers

Nov 01, 2023

7 Smart Strategies for Acing Board Examinations

Oct 18, 2023

How Can Schools Inculcate Social Responsibility Among Students?

Sep 20, 2023

Mahatma Gandhi Jayanti - History, Facts, Significance, Importance

Sep 13, 2023

ITI Courses After 12th - Course Duration & Top Institutes

Nov 16, 2023

10th Time Table 2024 - Download All Boards Class 10th Date Sheet Here

Nov 28, 2023

Diwali Essay: About Deepavali, Short Paragraphs, 10 Lines On Diwali

Nov 09, 2023

Children's Day 2023: Why Is It Celebrated, How Schools Can Celebrate

Sep 12, 2023

UPTAC Participating Institutes 2023 - Check here List of Colleges

Jul 27, 2023

How to join DRDO after 12th - A Complete Guide

Jul 03, 2023

Best Career Options For Girls - Check Eligibility, Salary, Qualification

Jun 21, 2023

UP Madarsa Board Result 2024 for Molvi, Munshi, Alim, Kamil & Fazil - UPBME Result Here

Nov 15, 2023

Explore Premium

Mental Health

Exam Preparation: Get Over Self-Doubt With These Effective Measures

5 min ⋆ Dec 02, 2023

Mental Health

Gandhian Principles Can Aid Mental Well-Being

3 min ⋆ Oct 21, 2023

Mental Health

Every Student Should Build On These Must Have Skills

3 min ⋆ Sep 23, 2023

Parenting

Why Children Should Be Trained In Disaster Preparedness

5 min ⋆ Dec 03, 2023

Parenting

Is Playschool Mandatory For Your Child’s Development?

5 min ⋆ Nov 26, 2023

Parenting

Parents, Don’t Shy Away From Talking Good And Bad Touch

5 min ⋆ Nov 19, 2023

Upcoming School Exams

All India Sainik Schools Entrance Examination

Application Date:06 November,2023 - 15 December,2023

Exam Pattern

Answer Key

Result

National Institute of Open Schooling 12th Examination

Application Date:20 November,2023 - 19 December,2023

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Application Date:20 November,2023 - 19 December,2023

Application Process

Exam Pattern

Mock Test

West Bengal Board 12th Examination

Exam Date:30 November,2023 - 14 December,2023

Result

Exam Pattern

Admit Card

National Science Olympiad

Exam Date:04 December,2023 - 04 December,2023

Exam Pattern

Result

Answer Key

View All School Exams

Get answers from students and experts

Explore Career Options (By Industry)

Data Administrator

Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.

4 Jobs Available

Bio Medical Engineer

The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary.

4 Jobs Available

Ethical Hacker

A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.

3 Jobs Available

Database Architect

If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi.

3 Jobs Available

Data Analyst

The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

3 Jobs Available

Geothermal Engineer

Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.

3 Jobs Available

Geotechnical engineer

The role of geotechnical engineer starts with reviewing the projects needed to define the required material properties. The work responsibilities are followed by a site investigation of rock, soil, fault distribution and bedrock properties on and below an area of interest. The investigation is aimed to improve the ground engineering design and determine their engineering properties that include how they will interact with, on or in a proposed construction.

The role of geotechnical engineer in mining includes designing and determining the type of foundations, earthworks, and or pavement subgrades required for the intended man-made structures to be made. Geotechnical engineering jobs are involved in earthen and concrete dam construction projects, working under a range of normal and extreme loading conditions.

3 Jobs Available

Cartographer

How fascinating it is to represent the whole world on just a piece of paper or a sphere. With the help of maps, we are able to represent the real world on a much smaller scale. Individuals who opt for a career as a cartographer are those who make maps. But, cartography is not just limited to maps, it is about a mixture of art, science, and technology. As a cartographer, not only you will create maps but use various geodetic surveys and remote sensing systems to measure, analyse, and create different maps for political, cultural or educational purposes.

3 Jobs Available

Bank Probationary Officer (PO)

A career as Bank Probationary Officer (PO) is seen as a promising career opportunity and a white-collar career. Each year aspirants take the Bank PO exam. This career provides plenty of career development and opportunities for a successful banking future. If you have more questions about a career as Bank Probationary Officer (PO), what is probationary officer or how to become a Bank Probationary Officer (PO) then you can read the article and clear all your doubts.

3 Jobs Available

Operations Manager

Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.

3 Jobs Available

Data Analyst

3 Jobs Available

Finance Executive

A career as a Finance Executive requires one to be responsible for monitoring an organisation's income, investments and expenses to create and evaluate financial reports. His or her role involves performing audits, invoices, and budget preparations. He or she manages accounting activities, bank reconciliations, and payable and receivable accounts.

3 Jobs Available

Investment Banker

An Investment Banking career involves the invention and generation of capital for other organizations, governments, and other entities. Individuals who opt for a career as Investment Bankers are the head of a team dedicated to raising capital by issuing bonds. Investment bankers are termed as the experts who have their fingers on the pulse of the current financial and investing climate. Students can pursue various Investment Banker courses, such as Banking and Insurance, and Economics to opt for an Investment Banking career path.

3 Jobs Available

Bank Branch Manager

Bank Branch Managers work in a specific section of banking related to the invention and generation of capital for other organisations, governments, and other entities. Bank Branch Managers work for the organisations and underwrite new debts and equity securities for all type of companies, aid in the sale of securities, as well as help to facilitate mergers and acquisitions, reorganisations, and broker trades for both institutions and private investors.

3 Jobs Available

Treasurer

Treasury analyst career path is often regarded as certified treasury specialist in some business situations, is a finance expert who specifically manages a company or organisation's long-term and short-term financial targets. Treasurer synonym could be a financial officer, which is one of the reputed positions in the corporate world. In a large company, the corporate treasury jobs hold power over the financial decision-making of the total investment and development strategy of the organisation.

3 Jobs Available

Product Manager

A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.

3 Jobs Available

Transportation Planner

A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.

3 Jobs Available

Conservation Architect

A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.

2 Jobs Available

Safety Manager

A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.

2 Jobs Available

Team Lead

A Team Leader is a professional responsible for guiding, monitoring and leading the entire group. He or she is responsible for motivating team members by providing a pleasant work environment to them and inspiring positive communication. A Team Leader contributes to the achievement of the organisation’s goals. He or she improves the confidence, product knowledge and communication skills of the team members and empowers them.

2 Jobs Available

Structural Engineer

A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.

2 Jobs Available

Architect

Individuals in the architecture career are the building designers who plan the whole construction keeping the safety and requirements of the people. Individuals in architect career in India provides professional services for new constructions, alterations, renovations and several other activities. Individuals in architectural careers in India visit site locations to visualize their projects and prepare scaled drawings to submit to a client or employer as a design. Individuals in architecture careers also estimate build costs, materials needed, and the projected time frame to complete a build.

2 Jobs Available

Landscape Architect

Having a landscape architecture career, you are involved in site analysis, site inventory, land planning, planting design, grading, stormwater management, suitable design, and construction specification. Frederick Law Olmsted, the designer of Central Park in New York introduced the title “landscape architect”. The Australian Institute of Landscape Architects (AILA) proclaims that "Landscape Architects research, plan, design and advise on the stewardship, conservation and sustainability of development of the environment and spaces, both within and beyond the built environment". Therefore, individuals who opt for a career as a landscape architect are those who are educated and experienced in landscape architecture. Students need to pursue various landscape architecture degrees, such as M.Des, M.Plan to become landscape architects. If you have more questions regarding a career as a landscape architect or how to become a landscape architect then you can read the article to get your doubts cleared.

2 Jobs Available

Plumber

An expert in plumbing is aware of building regulations and safety standards and works to make sure these standards are upheld. Testing pipes for leakage using air pressure and other gauges, and also the ability to construct new pipe systems by cutting, fitting, measuring and threading pipes are some of the other more involved aspects of plumbing. Individuals in the plumber career path are self-employed or work for a small business employing less than ten people, though some might find working for larger entities or the government more desirable.

2 Jobs Available

Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available

Veterinary Doctor

A veterinary doctor is a medical professional with a degree in veterinary science. The veterinary science qualification is the minimum requirement to become a veterinary doctor. There are numerous veterinary science courses offered by various institutes. He or she is employed at zoos to ensure they are provided with good health facilities and medical care to improve their life expectancy.

5 Jobs Available

Pathologist

A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.

5 Jobs Available

Gynaecologist

Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth.

4 Jobs Available

Surgical Technologist

When it comes to an operation theatre, there are several tasks that are to be carried out before as well as after the operation or surgery has taken place. Such tasks are not possible without surgical tech and surgical tech tools. A single surgeon cannot do it all alone. It’s like for a footballer he needs his team’s support to score a goal the same goes for a surgeon. It is here, when a surgical technologist comes into the picture. It is the job of a surgical technologist to prepare the operation theatre with all the required equipment before the surgery. Not only that, once an operation is done it is the job of the surgical technologist to clean all the equipment. One has to fulfil the minimum requirements of surgical tech qualifications.

Also Read: Career as Nurse

3 Jobs Available

Oncologist

An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.

3 Jobs Available

Chemical Pathologist

Are you searching for a chemical pathologist job description? A chemical pathologist is a skilled professional in healthcare who utilises biochemical laboratory tests to diagnose disease by analysing the levels of various components or constituents in the patient’s body fluid.

2 Jobs Available

Biochemical Engineer

A Biochemical Engineer is a professional involved in the study of proteins, viruses, cells and other biological substances. He or she utilises his or her scientific knowledge to develop products, medicines or ways to improve quality and refine processes. A Biochemical Engineer studies chemical functions occurring in a living organism’s body. He or she utilises the observed knowledge to alter the composition of products and develop new processes. A Biochemical Engineer may develop biofuels or environmentally friendly methods to dispose of waste generated by industries.

2 Jobs Available

Actor

For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs.

4 Jobs Available

Acrobat

Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.

3 Jobs Available

Video Game Designer

Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages. Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.

3 Jobs Available

Talent Agent

The career as a Talent Agent is filled with responsibilities. A Talent Agent is someone who is involved in the pre-production process of the film. It is a very busy job for a Talent Agent but as and when an individual gains experience and progresses in the career he or she can have people assisting him or her in work. Depending on one’s responsibilities, number of clients and experience he or she may also have to lead a team and work with juniors under him or her in a talent agency. In order to know more about the job of a talent agent continue reading the article.

If you want to know more about talent agent meaning, how to become a Talent Agent, or Talent Agent job description then continue reading this article.

3 Jobs Available

Radio Jockey

Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.

A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.

3 Jobs Available

Social Media Manager

A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.

2 Jobs Available

Choreographer

The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.

2 Jobs Available

Talent Director

Individuals who opt for a career as a talent director are professionals who work in the entertainment industry. He or she is responsible for finding out the right talent through auditions for films, theatre productions, or shows. A talented director possesses strong knowledge of computer software used in filmmaking, CGI and animation. A talent acquisition director keeps himself or herself updated on various technical aspects such as lighting, camera angles and shots.

2 Jobs Available

Copy Writer

In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook.

5 Jobs Available

Journalist

Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.

3 Jobs Available

Publisher

For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.

3 Jobs Available

Vlogger

In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion. Ever since internet cost got reduced the viewership for these types of content has increased on a large scale. Therefore, the career as vlogger has a lot to offer. If you want to know more about the career as vlogger, how to become a vlogger, so on and so forth then continue reading the article. Students can visit Jamia Millia Islamia, Asian College of Journalism, Indian Institute of Mass Communication to pursue journalism degrees.

3 Jobs Available

Editor

Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.

3 Jobs Available

Content Writer

Content writing is meant to speak directly with a particular audience, such as customers, potential customers, investors, employees, or other stakeholders. The main aim of professional content writers is to speak to their targeted audience and if it is not then it is not doing its job. There are numerous kinds of the content present on the website and each is different based on the service or the product it is used for.

2 Jobs Available

Reporter

Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.

2 Jobs Available

Linguist

Linguistic meaning is related to language or Linguistics which is the study of languages. A career as a linguistic meaning, a profession that is based on the scientific study of language, and it's a very broad field with many specialities. Famous linguists work in academia, researching and teaching different areas of language, such as phonetics (sounds), syntax (word order) and semantics (meaning).

Other researchers focus on specialities like computational linguistics, which seeks to better match human and computer language capacities, or applied linguistics, which is concerned with improving language education. Still, others work as language experts for the government, advertising companies, dictionary publishers and various other private enterprises. Some might work from home as freelance linguists. Philologist, phonologist, and dialectician are some of Linguist synonym. Linguists can study French, German, Italian.

2 Jobs Available

Production Manager

Production Manager Job Description: A Production Manager is responsible for ensuring smooth running of manufacturing processes in an efficient manner. He or she plans and organises production schedules. The role of Production Manager involves estimation, negotiation on budget and timescales with the clients and managers.

Resource Links for Online MBA

3 Jobs Available

Product Manager

3 Jobs Available

Quality Controller

A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product.

A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.

3 Jobs Available

Production Engineer

A career as Production Engineer is crucial in the manufacturing industry. He or she ensures the functionality of production equipment and machinery to improve productivity and minimize production costs in order to drive revenues and increase profitability.

2 Jobs Available

Automation Test Engineer

An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process.

2 Jobs Available

Product Designer

Individuals who opt for a career as product designers are responsible for designing the components and overall product concerning its shape, size, and material used in manufacturing. They are responsible for the aesthetic appearance of the product. A product designer uses his or her creative skills to give a product its final outlook and ensures the functionality of the design.

Students can opt for various product design degrees such as B.Des and M.Des to become product designers. Industrial product designer prepares 3D models of designs for approval and discusses them with clients and other colleagues. Individuals who opt for a career as a product designer estimate the total cost involved in designing.

2 Jobs Available

R&D Personnel

A career as R&D Personnel requires researching, planning, and implementing new programs and protocols into their organization and overseeing new products’ development. He or she uses his or her creative abilities to improve the existing products as per the requirements of the target market.

2 Jobs Available

Commercial Manager

A Commercial Manager negotiates, advises and secures information about pricing for commercial contracts. He or she is responsible for developing financial plans in order to maximise the business's profitability.

2 Jobs Available

Product Manager

3 Jobs Available

ITSM Manager

ITSM Manager is a professional responsible for heading the ITSM (Information Technology Service Management) or (Information Technology Infrastructure Library) processes. He or she ensures that operation management provides appropriate resource levels for problem resolutions. The ITSM Manager oversees the level of prioritisation for the problems, critical incidents, planned as well as proactive tasks.

3 Jobs Available

Information Security Manager

Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack

3 Jobs Available

Computer Programmer

Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.

3 Jobs Available

Computer System Analyst

Individuals in the computer systems analyst career path study the hardware and applications that are part of an organization's computer systems, as well as how they are used. They collaborate closely with managers and end-users to identify system specifications and business priorities, as well as to assess the efficiency of computer systems and create techniques to boost IT efficiency. Individuals who opt for a career as a computer system analyst support the implementation, modification, and debugging of new systems after they have been installed.

2 Jobs Available

Test Manager

A Test Manager is a professional responsible for planning, coordinating and controlling test activities. He or she develops test processes and strategies to analyse and determine test methods and tools for test activities. The test manager jobs involve documenting tests that have been carried out, analysing and evaluating software quality to determine further recommended procedures.

2 Jobs Available

Azure Developer

A career as Azure Developer comes with the responsibility of designing and developing cloud-based applications and maintaining software components. He or she possesses an in-depth knowledge of cloud computing and Azure app service.

2 Jobs Available

Deep Learning Engineer

A Deep Learning Engineer is an IT professional who is responsible for developing and managing data pipelines. He or she is knowledgeable about analyzing and storing data collected from various sources. A Career as a Deep Learning Engineer needs to help the data scientists and analysts to create effective data sets.

2 Jobs Available

Applications for Admissions are open.

NEET 2024 Most scoring concepts

Apply

Just Study 32% of the NEET syllabus and Score upto 100% marks

ETS ® TOEFL ®

Apply

Thinking of Studying Abroad? Think the TOEFL® test & make your dreams come true

JEE Main high scoring chapters and topics

Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

NEET previous year papers with solutions

Apply

Solve NEET previous years question papers & check your preparedness

JEE Main Important Mathematics Formulas

Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

JEE Main Important Physics formulas

Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

View All Application Forms

News and Notifications

37,484 chairs, 6,246 desks ordered for 800 schools of MCD: Official

22/09/2023, 02:01:05

CBI books Kendriya Vidyalaya principal for admitting 193 students on fake certificates

21/09/2023, 17:04:41

Aadhaar card not mandatory for EWS admission in private schools: Delhi High Court

21/09/2023, 11:34:59

25 Assam schools have 0 students; those lacking ‘sustainable' enrolment will be merged, says Ranoj Pegu

21/09/2023, 11:15:37

Tamil Nadu Rains: Schools closed in Vellore for Class 1 to 5 due to heavy rainfall

21/09/2023, 05:22:28

MCD to open 5 new schools soon, start work on 5 more by December: Officials

20/09/2023, 17:20:17

Odisha primary school teachers to hold demonstration outside assembly on September 26

20/09/2023, 16:17:14

Everything about Education

Latest updates, Exclusive Content, Webinars and more.

Subscribe to Premium

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

250M+
Students
30,000+
Colleges
500+
Exams
1500+
E-Books
12000+
Cetifications

We Appeared in

Explore Top Colleges Accepting Applications

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Animation Courses

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Exercise 9.4 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles

Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.1

More About NCERT Solutions for Class 9 Maths Exercise 9.4

Benefits of NCERT Solutions for Class 9 Maths Exercise 9.4

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

Also Read

Articles

Explore Premium

Exam Preparation: Get Over Self-Doubt With These Effective Measures

Gandhian Principles Can Aid Mental Well-Being

Every Student Should Build On These Must Have Skills

Why Children Should Be Trained In Disaster Preparedness

Is Playschool Mandatory For Your Child’s Development?

Parents, Don’t Shy Away From Talking Good And Bad Touch

Upcoming School Exams

All India Sainik Schools Entrance Examination