NCERT Solutions for Exercise 9.3 Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles
The NCERT Solutions for Class 9 Maths exercise 9.3 deal with triangles rather than parallelograms. In Class 9 Maths chapter 9 exercise 9.3 we deal with triangles that have a common base and are in the same parallels.
This Story also Contains
- Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.3
- More About NCERT Solutions for Class 9 Maths Exercise 9.3
- Benefits of NCERT Solutions for Class 9 Maths Exercise 9.3
- NCERT Solutions of Class 10 Subject Wise
- Subject Wise NCERT Exemplar Solutions
The important concepts related to NCERT solutions for Class 9 Maths chapter 9 exercise 9.3 in order to solve this exercise are:
Triangles that have the same base or the equal base and are between the same parallel lines have equivalent areas. This is on the grounds that we realize that the space of the triangle is half of the product of base and tallness since the height (distance between the parallels) remains the same for the two triangles and they have the same bases thus their areas are equal.
The figure shown below is a set of triangles with the same base and between the same parallel
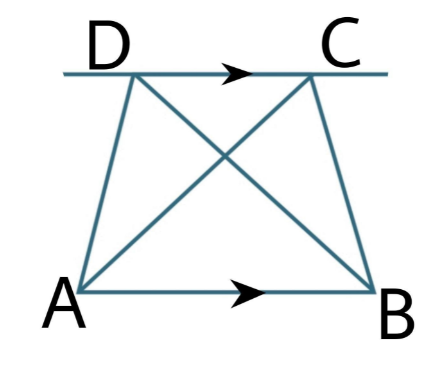
The triangles ABC and BCD have the same area.
Along with NCERT book exercise 9.3 Class 9 Maths, the following exercises are also present.
Areas Of Parallelograms And Triangles Class 9 Chapter 9 Exercise: 9.3
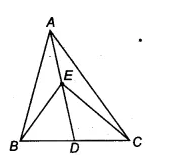
Answer: ![]()
We have $\Delta$ ABC such that AD is a median. And we know that median divides the triangle into two triangles of equal areas.
Therefore, ar( $\Delta$ ABD) = ar( $\Delta$ ACD)............(i)
Similarly, In triangle $\Delta$ BEC,
ar( $\Delta$ BED) = ar ( $\Delta$ DEC)................(ii)
On subtracting eq(ii) from eq(i), we get
ar( $\Delta$ ABD) - ar( $\Delta$ BED) =
$\small ar(ABE)=ar(ACE)$
Hence proved.
Q2 In a triangle ABC, E is the mid-point of median AD. Show that $\small ar(BED)=\frac{1}{4}ar(ABC)$ .
Answer:
We have a triangle ABC and AD is a median. Join B and E. 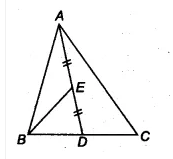
![]()
Since the median divides the triangle into two triangles of equal area.
$\therefore$ ar( $\Delta$ ABD) = ar ( $\Delta$ ACD) = 1/2 ar( $\Delta$ ABC)..............(i)
Now, in triangle $\Delta$ ABD,
BE is the median [since E is the midpoint of AD]
$\therefore$ ar ( $\Delta$ BED) = 1/2 ar( $\Delta$ ABD)........(ii)
From eq (i) and eq (ii), we get
ar ( $\Delta$ BED) = 1/2 . (1/2 ar(ar ( $\Delta$ ABC))
ar ( $\Delta$ BED) = 1/4 .ar( $\Delta$ ABC)
Hence proved.
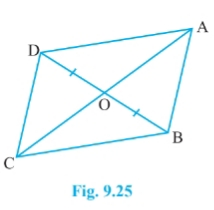
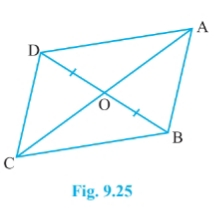
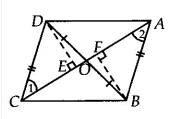
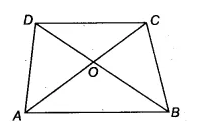
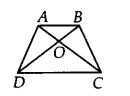
Q3 Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer:
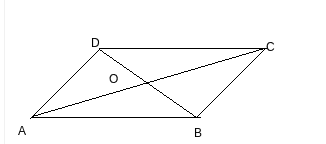
![]()
Let ABCD is a parallelogram. So, AB || CD and AD || BC and we know that Diagonals bisects each other. Therefore, AO = OC and BO = OD
Since OD = BO
Therefore, ar ( $\Delta$ BOC) = ar ( $\Delta$ DOC)...........(a) ( since OC is the median of triangle CBD)
Similarly, ar( $\Delta$ AOD) = ar( $\Delta$ DOC) ............(b) ( since OD is the median of triangle ACD)
and, ar ( $\Delta$ AOB) = ar( $\Delta$ BOC)..............(c) ( since OB is the median of triangle ABC)
From eq (a), (b) and eq (c), we get
ar ( $\Delta$ BOC) = ar ( $\Delta$ DOC)= ar( $\Delta$ AOD) = ( $\Delta$ AOB)
Thus, the diagonals of ||gm divide it into four equal triangles of equal area.
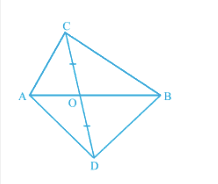
![]()
Answer:
We have, $\Delta$ ABC and $\Delta$ ABD on the same base AB. CD is bisected by AB at point O.
$\therefore$ OC = OD
Now, in $\Delta$ ACD, AO is median
$\therefore$ ar ( $\Delta$ AOC) = ar ( $\Delta$ AOD)..........(i)
Similarly, in $\Delta$ BCD, BO is the median
$\therefore$ ar ( $\Delta$ BOC) = ar ( $\Delta$ BOD)............(ii)
Adding equation (i) and eq (ii), we get
ar ( $\Delta$ AOC) + ar ( $\Delta$ BOC) = ar ( $\Delta$ AOD) + ar ( $\Delta$ BOD)
$\small ar(ABC)=ar(ABD)$
Hence proved.
Answer:
We have a triangle $\Delta$ ABC such that D, E and F are the midpoints of the sides BC, CA and AB respectively. 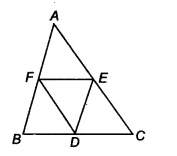
![]()
Now, in $\Delta$ ABC,
F and E are the midpoints of the side AB and AC.
Therefore according to mid-point theorem, the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half of the third side.
$\therefore$ EF || BC or EF || BD
also, EF = 1/2 (BC)
$\Rightarrow EF = BD$ [ D is the midpoint of BC]
Similarly, ED || BF and ED = FB
Hence BDEF is a parallelogram.
$\small ar(DEF)=\frac{1}{4}ar(ABC)$
Answer:
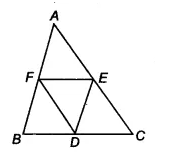
![]()
We already proved that BDEF is a ||gm.
Similarly, DCEF and DEAF are also parallelograms.
Now, ||gm BDEF and ||gm DCEF is on the same base EF and between same parallels BC and EF
$\therefore$ Ar (BDEF) = Ar (DCEF)
$\Rightarrow$ Ar( $\Delta$ BDF) = Ar ( $\Delta$ DEF) .............(i)
It is known that diagonals of ||gm divides it into two triangles of equal area.
$\therefore$ Ar(DCE) = Ar (DEF).......(ii)
and, Ar( $\Delta$ AEF) = Ar ( $\Delta$ DEF)...........(iii)
From equation(i), (ii) and (iii), we get
Ar( $\Delta$ BDF) = Ar(DCE) = Ar( $\Delta$ AEF) = Ar ( $\Delta$ DEF)
Thus, Ar ( $\Delta$ ABC) = Ar( $\Delta$ BDF) + Ar(DCE) + Ar( $\Delta$ AEF) + Ar ( $\Delta$ DEF)
Ar ( $\Delta$ ABC) = 4 . Ar( $\Delta$ DEF)
$\Rightarrow$ $ar(\Delta DEF) = \frac{1}{4}ar(\Delta ABC)$
Hence proved.
$\small ar(BDEF)=\frac{1}{2}ar(ABC)$
Answer:
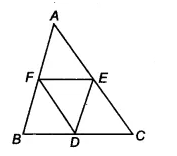
![]()
Since we already proved that,
ar( $\Delta$ DEF) = ar ( $\Delta$ BDF).........(i)
So, ar(||gm BDEF) = ar( $\Delta$ BDF) + ar ( $\Delta$ DEF)
= 2 . ar( $\Delta$ DEF) [from equation (i)]
$\\= 2[\frac{1}{4}ar(\Delta ABC)]\\ =\frac{1}{2} ar(\Delta ABC)$
Hence proved.
[ Hint: From D and B, draw perpendiculars to AC.]
 Answer:
Answer:
We have ABCD is quadrilateral whose diagonals AC and BD intersect at O. And OB = OD, AB = CD
Draw DE $\perp$ AC and FB $\perp$ AC 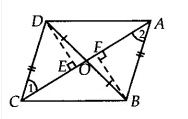
![]()
In $\Delta$ DEO and $\Delta$ BFO
$\angle$ DOE = $\angle$ BOF [vertically opposite angle]
$\angle$ OED = $\angle$ BFO [each $90^0$ ]
OB = OD [given]
Therefore, by AAS congruency
$\Delta$ DEO $\cong$ $\Delta$ BFO
$\Rightarrow$ DE = FB [by CPCT]
and ar( $\Delta$ DEO) = ar( $\Delta$ BFO) ............(i)
Now, In $\Delta$ DEC and $\Delta$ ABF
$\angle$ DEC = $\angle$ BFA [ each $90^0$ ]
DE = FB
DC = BA [given]
So, by RHS congruency
$\Delta$ DEC $\cong$ $\Delta$ BFA
$\angle$ 1 = $\angle$ 2 [by CPCT]
and, ar( $\Delta$ DEC) = ar( $\Delta$ BFA).....(ii)
By adding equation(i) and (ii), we get
$\small ar(DOC)=ar(AOB)$
Hence proved.
[ Hint: From D and B, draw perpendiculars to AC.]
Answer:
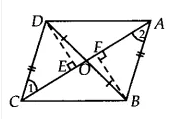
![]()
We already proved that,
$ar(\Delta DOC)=ar(\Delta AOB)$
Now, add $ar(\Delta BOC)$ on both sides we get
$\\ar(\Delta DOC)+ar(\Delta BOC)=ar(\Delta AOB)+ar(\Delta BOC)\\ ar(\Delta DCB) = ar (\Delta ACB)$
Hence proved.
$\small DA\parallel CB$ or ABCD is a parallelogram.
[ Hint : From D and B, draw perpendiculars to AC.]
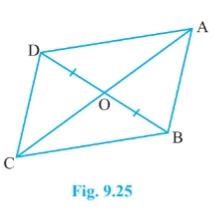
Answer:
![]()
Since $\Delta$ DCB and $\Delta$ ACB both lie on the same base BC and having equal areas.
Therefore, They lie between the same parallels BC and AD
$\Rightarrow$ CB || AD
also $\angle$ 1 = $\angle$ 2 [ already proved]
So, AB || CD
Hence ABCD is a || gm
Answer:
We have $\Delta$ ABC and points D and E are on the sides AB and AC such that ar( $\Delta$ DBC ) = ar ( $\Delta$ EBC)
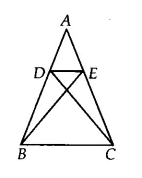
![]()
Since $\Delta$ DBC and $\Delta$ EBC are on the same base BC and having the same area.
$\therefore$ They must lie between the same parallels DE and BC
Hence DE || BC.
Answer:
We have a $\Delta$ ABC such that BE || AC and CF || AB
Since XY || BC and BE || CY
Therefore, BCYE is a ||gm
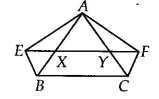 Now, The ||gm BCEY and $\Delta$ ABE are on the same base BE and between the same parallels AC and BE.
Now, The ||gm BCEY and $\Delta$ ABE are on the same base BE and between the same parallels AC and BE.
$\therefore$ ar( $\Delta$ AEB) = 1/2 .ar(||gm BEYC)..........(i)
Similarly, ar( $\Delta$ ACF) = 1/2 . ar(||gm BCFX)..................(ii)
Also, ||gm BEYC and ||gmBCFX are on the same base BC and between the same parallels BC and EF.
$\therefore$ ar (BEYC) = ar (BCFX).........(iii)
From eq (i), (ii) and (iii), we get
ar( $\Delta$ ABE) = ar( $\Delta$ ACF)
Hence proved.
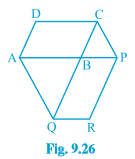 Answer:
Answer:
Join the AC and PQ. 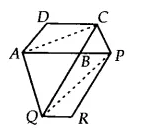
![]()
It is given that ABCD is a ||gm and AC is a diagonal of ||gm
Therefore, ar( $\Delta$ ABC) = ar( $\Delta$ ADC) = 1/2 ar(||gm ABCD).............(i)
Also, ar( $\Delta$ PQR) = ar( $\Delta$ BPQ) = 1/2 ar(||gm PBQR).............(ii)
Since $\Delta$ AQC and $\Delta$ APQ are on the same base AQ and between same parallels AQ and CP.
$\therefore$ ar( $\Delta$ AQC) = ar ( $\Delta$ APQ)
Now, subtracting $\Delta$ ABQ from both sides we get,
ar( $\Delta$ AQC) - ar ( $\Delta$ ABQ) = ar ( $\Delta$ APQ) - ar ( $\Delta$ ABQ)
ar( $\Delta$ ABC) = ar ( $\Delta$ BPQ)............(iii)
From eq(i), (ii) and (iii) we get
$\small ar(ABCD)=ar(PBQR)$
Hence proved.
Answer:
![]()
We have a trapezium ABCD such that AB || CD and it's diagonals AC and BD intersect each other at O
$\Delta$ ABD and $\Delta$ ABC are on the same base AB and between same parallels AB and CD
$\therefore$ ar( $\Delta$ ABD) = ar ( $\Delta$ ABC)
Now, subtracting $\Delta$ AOB from both sides we get
ar ( $\Delta$ AOD) = ar ( $\Delta$ BOC)
Hence proved.
(i) $\small ar(ACB)=ar(ACF)$
(ii) $\small ar(AEDF)=ar(ABCDE)$
![]()
Answer:
We have a pentagon ABCDE in which BF || AC and CD is produced to F.
(i) Since $\Delta$ ACB and $\Delta$ ACF are on the same base AC and between same parallels AC and FB.
$\therefore$ ar( $\Delta$ ACB) = ar ( $\Delta$ ACF)..................(i)
(ii) Adding the ar (AEDC) on both sides in equation (i), we get
ar( $\Delta$ ACB) + ar(AEDC) = ar ( $\Delta$ ACF) + ar(AEDC)
$\therefore$ $\small ar(AEDF)=ar(ABCDE)$
Hence proved.
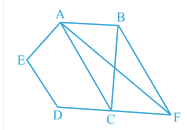
Answer:
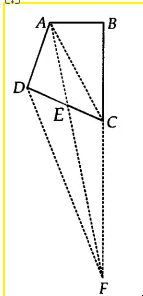
![]()
We have a quadrilateral shaped plot ABCD. Draw DF || AC and AF || CF.
Now, $\Delta$ DAF and $\Delta$ DCF are on the same base DF and between same parallels AC and DF.
$\therefore$ ar ( $\Delta$ DAF) = ar( $\Delta$ DCF)
On subtracting $\Delta$ DEF from both sides, we get
ar( $\Delta$ ADE) = ar( $\Delta$ CEF)...............(i)
The portion of $\Delta$ ADE can be taken by the gram panchayat and on adding the land $\Delta$ CEF to his (Itwaari) land so as to form a triangular plot.( $\Delta$ ABF)
We need to prove that ar( $\Delta$ ABF) = ar (quad. ABCD)
Now, adding ar(quad. ABCE) on both sides in eq (i), we get
ar ( $\Delta$ ADE) + ar(quad. ABCE) = ar( $\Delta$ CEF) + ar(quad. ABCE)
ar (ABCD) = ar( $\Delta$ ABF)
Answer:
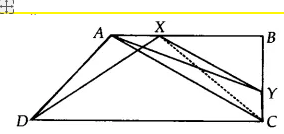
![]()
We have a trapezium ABCD, AB || CD
XY ||AC meets AB at X and BC at Y. Join XC
Since $\Delta$ ADX and $\Delta$ ACX lie on the same base CD and between same parallels AX and CD
Therefore, ar( $\Delta$ ADX) = ar( $\Delta$ ACX)..........(i)
Similarly ar( $\Delta$ ACX) = ar( $\Delta$ ACY).............(ii) [common base AC and AC || XY]
From eq (i) and eq (ii), we get
ar( $\Delta$ ADX) = ar ( $\Delta$ ACY)
Hence proved.
Q14 In Fig. $\small 9.28$ , $\small AP\parallel BQ\parallel CR$ . Prove that $\small ar(AQC)=ar(PBR)$ .
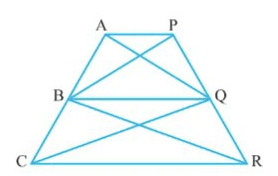
![]()
Answer:
We have, AP || BQ || CR
$\Delta$ BCQ and $\Delta$ BQR lie on the same base (BQ) and between same parallels (BQ and CR)
Therefore, ar ( $\Delta$ BCQ) = ar ( $\Delta$ BQR)........(i)
Similarly, ar ( $\Delta$ ABQ) = ar ( $\Delta$ PBQ) [common base BQ and BQ || AP]............(ii)
Add the eq(i) and (ii), we get
ar ( $\Delta$ AQC) = ar ( $\Delta$ PBR)
Hence proved.
Answer:
![]()
We have,
ABCD is a quadrilateral and diagonals AC and BD intersect at O such that ar( $\Delta$ AOD) = ar ( $\Delta$ BOC) ...........(i)
Now, add ar ( $\Delta$ BOA) on both sides, we get
ar( $\Delta$ AOD) + ar ( $\Delta$ BOA) = ar ( $\Delta$ BOA) + ar ( $\Delta$ BOC)
ar ( $\Delta$ ABD) = ar ( $\Delta$ ABC)
Since the $\Delta$ ABC and $\Delta$ ABD lie on the same base AB and have an equal area.
Therefore, AB || CD
Hence ABCD is a trapezium.
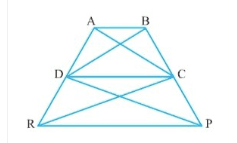
![]()
Answer:
Given,
ar( $\Delta$ DPC) = ar( $\Delta$ DRC) ..........(i)
and ar( $\Delta$ BDP) = ar(ARC)............(ii)
from equation (i),
Since $\Delta$ DRC and $\Delta$ DPC lie on the same base DC and between same parallels.
$\therefore$ CD || RP (opposites sides are parallel)
Hence quadrilateral DCPR is a trapezium
Now, by subtracting eq(ii) - eq(i) we get
ar( $\Delta$ BDP) - ar( $\Delta$ DPC) = ar( $\Delta$ ARC) - ar( $\Delta$ DRC)
ar( $\Delta$ BDC) = ar( $\Delta$ ADC) (Since theya are on the same base DC)
$\Rightarrow$ AB || DC
Hence ABCD is a trapezium.
More About NCERT Solutions for Class 9 Maths Exercise 9.3
From NCERT solutions for Class 9 Maths exercise 9.3, we get to know another concept (theorem) which deals with the converse of the above concept. We get to know that if two triangles have the same base (or if they have an equal base) and if they have equal areas then they lie on the same parallel line. Thus, a quick thing to remember from NCERT solutions for Class 9 Maths exercises 9.3 is that if the triangle has a median (a line that divides the base into two parts), then the median divides the triangle into two parts both on each side.
Also Read| Areas Of Parallelograms And Triangles Class 9 Notes
Benefits of NCERT Solutions for Class 9 Maths Exercise 9.3
Exercise 9.3 Class 9 Maths, is based on the AREAS OF PARALLELOGRAMS AND TRIANGLES by providing us with a general (much simpler) approach to calculate the area of triangles and parallelograms and concepts of figures in the same base and same parallel lines.
NCERT syllabus Class 9 Maths chapter 9 exercise 9.3 introduces us to a new concept of triangles on the same base and between the same parallels and its properties, like calculating the area and height.
- Understanding the concepts from Class 9 Maths chapter 9 exercise 9.3 will help us to compare the areas in multiple-choice questions easily and thus save time for a particular question.
Also, See
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
