NCERT Solutions for Class 9 Maths Chapter 6 Lines And Angles
The world of geometry starts with lines and angles. From a triangle to a circle, all depend on lines and angles. Have you ever looked down a long, straight road that seems to go on and on, wondering where the end is? Have you ever noticed that the clock hands at exactly 3 o'clock form a perfect 90-degree angle? These are just a couple of examples of where we see lines and angles, although we are completely unaware of them in our everyday lives. This chapter deals with lines, angles and their properties. The primary benefit of using NCERT Solutions for Class 9 is that they offer clear explanations and accurate answers, facilitating a deeper understanding.
This Story also Contains
- Lines And Angles Class 9 Questions And Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 6 Lines And Angles: Exercise Questions
- Lines and Angles Class 9 NCERT Solutions: Exercise-wise
- Class 9 Maths NCERT Chapter 6: Extra Question
- Lines And Angles Class 9 Chapter 6: Topics
- Lines And Angles Class 9 Solutions: Important Points
- Approach to Solve Questions of Lines and Angles Class 9
- NCERT Solutions for Class 9 Mathematics: Chapter-wise
Geometry begins when lines and angles combine to create a whole new world of patterns. Experienced Careers360 experts created these Class 9 NCERT solutions for lines and angles, aligning with the latest NCERT syllabus. Many teachers recommend NCERT Solutions because they closely match the exam pattern. Lines and angles have various applications in our daily lives. Having the basic concepts clear will be beneficial for the Class 9 board exams and day-to-day life. After going through all the NCERT Solutions for Class 9 Maths, students can practice the NCERT Exemplar Solutions for a deeper understanding of the concepts. Along with this, students can practise diagram-based questions and prove angle-based properties confidently. For syllabus, notes, and Exemplar solutions, refer to this NCERT article.
Lines And Angles Class 9 Questions And Answers PDF Free Download
These NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 9 Maths Chapter 6 Lines And Angles: Exercise Questions
NCERT Class 9 Maths Chapter 6 Lines and Angles question answers with detailed explanations are provided below.
|
Lines And Angles Class 9 Question Answers: Exercise: 6.1
Total Questions: 6
Page number: 76-77
|
Answer:

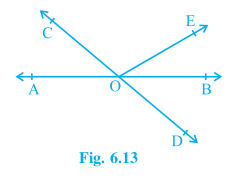
Given that,
AB is a straight line. Lines AB and CD intersect at O.
$\angle AOC + \angle BOE = 70°$ and $\angle$ BOD = $40°$
Since AB is a straight line,
$\therefore$ $\angle$ AOC + $\angle$ COE + $\angle$ EOB = $180°$
$\Rightarrow \angle COE = 180°-70°=110°$
[since $\angle AOC + \angle BOE = 70°$ ]
So, reflex $\angle$ COE = $360°-110° = 250°$
It is given that AB and CD intersect at O.
Therefore, $\angle$ AOC = $\angle$ BOD [vertically opposite angle]
$\Rightarrow \angle COA = 40°$ [ GIven $\angle$ BOD = $40°$ ]
Also, $\angle AOC + \angle BOE = 70°$
So, $\angle$ BOE = $30°$
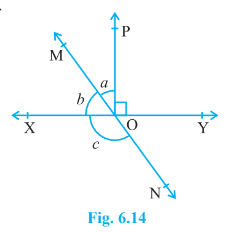
Question 2: In Fig. 6.14, lines XY and MN intersect at O. If $\angle POY = 90^o$ and a: b = 2 : 3, find c.
Answer:
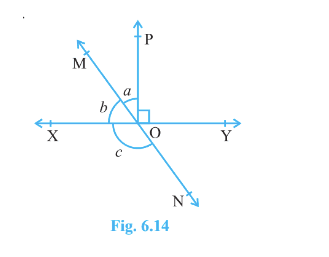
Given that,
Line XY and MN intersect at O and $\angle$ POY = $90°$
Also, $a:b = 2:3 \Rightarrow b = \frac{3a}{2}$ ..............(I)
Since XY is a straight line
Therefore, $\\a+b+\angle POY = 180°$
$\Rightarrow a+b = 180°-90° = 90°$ ...........(ii
Thus, from eq (i) and eq (ii), we get,
$\Rightarrow \frac{3a}{2}+a = 90°\\$
$\Rightarrow a = 36°\\$
So, $b = 54°\\$
Since $\angle$ MOY = $\angle$ c [vertically opposite angles]
$\angle$ a + $\angle$ POY = c
$126° =c$
Question 3: In Fig. 6.15, $\angle$ PQR = $\angle$ PRQ, then prove that $\angle$ PQS = $\angle$ PRT.
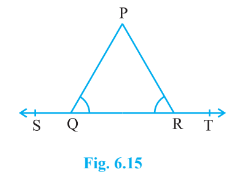
Answer:
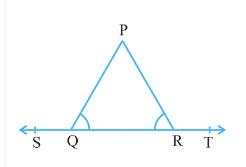
Given that,
ABC is a triangle such that $\angle$ PQR = $\angle$ PRQ, and ST is a straight line.
Now, $\angle$ PQR + $\angle$ PQS = $180°$ {Linear pair}............(I)
Similarly, $\angle$ PRQ + $\angle$ PRT = $180°$ ..................(ii)
Equating equations (i) and (ii), we get,
$\angle PQR +\angle PQS =\angle PRT + \angle PRQ$ {but $\angle$ PQR = $\angle$ PRQ }
Therefore, $\angle$ PQS = $\angle$ PRT
Hence, it is proved.
Question 4: In Fig. 6.16, ifx + y = w + z, then prove that AOB is a line.
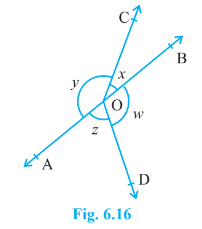
Answer:
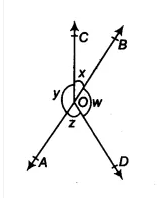
Given that,
$x+y = z+w$ ..............(I)
It is known that the sum of all the angles at a point = $360°$
$\therefore$ $x+y+z+w=360°$ ..............(ii)
From eq (i) and eq (ii), we get,
$\\2(x+y)=360°$
$\Rightarrow x+y = 180°$
Hence, it has been proven that AOB is a line.
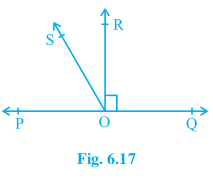
Answer:
Given that,
POQ is a line, OR $\perp$ PQ and $\angle$ ROQ is a right angle.
Now, $\angle$ POS + $\angle$ ROS + $\angle$ ROQ = $180°$ [since POQ is a straight line]
$\\\Rightarrow \angle POS + \angle ROS = 90°$
$ \Rightarrow \angle ROS = 90°-\angle POS$ .............(I)
and, $\angle$ ROS + $\angle$ ROQ = $\angle$ QOS
$\angle ROS = \angle QOS -90°$ ..............(ii)
Adding the eq (i ) and eq (ii), we get,
$\angle \textup{ROS} = \frac{1}{2}(\angle \textup{QOS} - \angle \textup{POS})$
Hence, proved.
Answer:
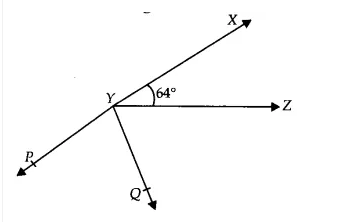
Given that,
$\angle$ XYZ = $64°$ and XY produced to point P and Ray YQ bisects $\angle$ ZYP $\Rightarrow \angle QYP = \angle ZYQ$
Now, XYP is a straight line.
So, $\angle$ XYZ + $\angle$ ZYQ + $\angle$ QYP = $180°$
$\Rightarrow 2(\angle QYP )=180° - 64° = 116°$
$\Rightarrow (\angle QYP )= 58°$
Thus reflex of $\angle$ QYP = $360°- 58° = 302°$
Since $\angle$ XYQ = $\angle$ XYZ + $\angle$ ZYQ
[ $\because$ $\angle QYP = \angle ZYQ$]
$\angle XYQ$ = $64°+58° = 122°$
|
Lines And Angles Class 9 Question Answers: Exercise: 6.2
Total Questions: 5
Page number: 80-81
|
Question 1: In Fig. 6.29, if AB $||$ CD, CD $||$ EF and y : z = 3 : 7 , find x .
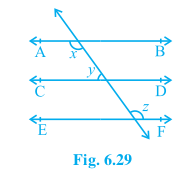
Answer:
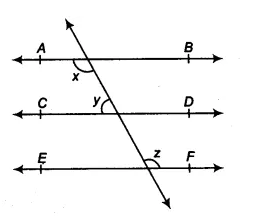
Given AB || CD and CD || EF and $y:z = 3:7$
$ \Rightarrow z = \frac{7}{3}y$
Therefore, AB || EF and $x =z$ (alternate interior angles)..............(i)
Again, CD || AB
$\\\Rightarrow x+y =180°$
$ \Rightarrow z+y =180°$ .............(ii)
Putting the value of $z$ in equation (ii), we get,
$\frac{10}{3}y =180°$
$ \Rightarrow y =54°$
Then $z=180°-54°=126°$
By equation (i), we get the value of $x=126°$
Answer:
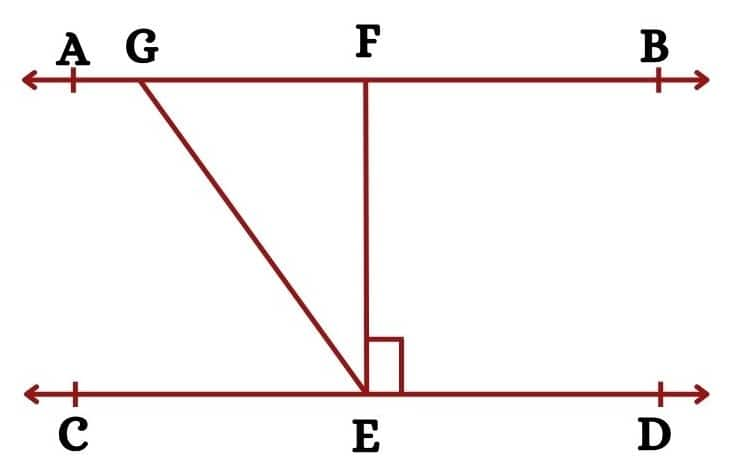
Given AB || CD, EF $\perp$ CD and $\angle$ GED = $126°$
In the above figure,
GE is transversal.
So, that $\angle$ AGE = $\angle$ GED = $126°$
[Alternate interior angles]
Also, $\angle$ GEF = $\angle$ GED - $\angle$ FED = $126°-90° = 36°$
$\Rightarrow \angle GEF = 36°$
Since AB is a straight line.
Therefore, $\angle$ AGE + $\angle$ FGE = $180°$
So, $\angle$ FGE = $180°-\angle AGE = 180° - 126°$
$\Rightarrow \angle FGE =54°$
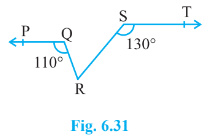
Answer:
Draw a line EF parallel to the ST through R.
Since PQ || ST and ST || EF
$\Rightarrow$ EF || PQ
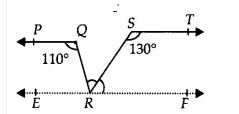
$\angle$ PQR = $\angle$ QRF = $110°$(Alternate interior angles)
$\angle$ QRF = $\angle$ QRS + $\angle$ SRF .............(i)
Again, $\angle$ RST + $\angle$ SRF = $180°$ (Interior angles of two parallels ST and RF)
$\Rightarrow \angle SRF =180°-130° = 50°$ ( $\angle$ RST = $130°$ , given)
Thus, $\angle$ QRS = $110°-50° = 60°$
Question 4: In Fig. 6.32, if AB $||$ CD, $\angle$ APQ = 50° and $\angle$ PRD = 127°, find x and y.
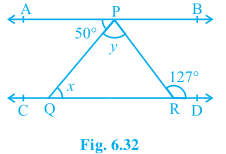
Answer:
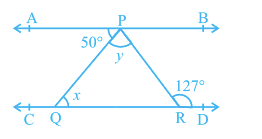
Given, AB || CD, $\angle$ APQ = $50°$ and $\angle$ PRD = $127°$
PQ is a transversal.
So,
$\angle$ APQ = $\angle$ PQR= $50°$ (alternate interior angles)
$\therefore x = 50°$
Again, PR is a transversal.
So,
$\angle$ y + $50°$ = $127°$ (Alternate interior angles)
$\Rightarrow y = 77°$

Answer:
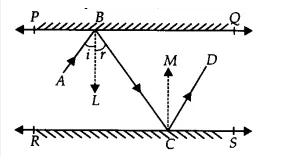
Draw a ray BL $\perp$ PQ and CM $\perp$ RS
Since PQ || RS (Given)
So, BL || CM and BC are a transversal.
$\therefore$ $\angle$ LBC = $\angle$ MCB (Alternate interior angles).............(I)
It is known that the angle of incidence = angle of reflection
So, $\angle$ ABL = $\angle$ LBC and $\angle$ MCB = $\angle$ MCD
$\Rightarrow \angle ABL =\angle MCD$ ..................(ii)
Adding equations (i) and (ii), we get,
$\angle$ ABC = $\angle$ DCB
Both the interior angles are equal
Hence AB || CD
Lines and Angles Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Lines and Angles Class 9 Maths Chapter 6 are provided in the link below.
Class 9 Maths NCERT Chapter 6: Extra Question
Question: In the figure, $\angle POR$ and $\angle QOR$ form a linear pair. If a° - b° = 90°, find the values of a and b.
Answer:
Given: $\angle POR$ + $\angle QOR$ = 180°
It means a° + b° = 180°..................(i)
And, a° - b° = 90° ..................(ii)
Now, adding (i) and (ii), we get;
2a° = 270°
Therefore, a° = 135°
And, thus b° = 180° - 135° = 45°
Lines And Angles Class 9 Chapter 6: Topics
The topics discussed in the NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles are:
- Introduction
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Pairs of Angles
- Lines Parallel to the Same Line
- Summary
Lines And Angles Class 9 Solutions: Important Points
Line
A straight one-dimensional figure that extends infinitely in both directions without any thickness or curvature is called a Line. A line does not curve or bend and can be horizontal or vertical.
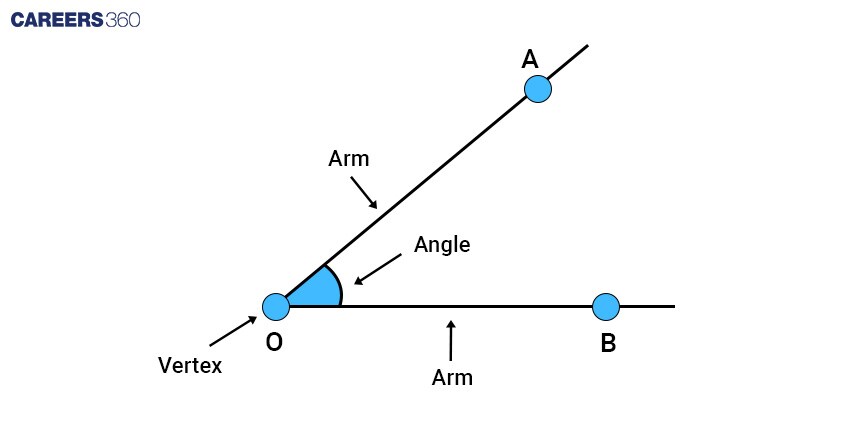
Angle
An angle is a fundamental concept in geometry that describes the figure formed by two rays or line segments sharing a common endpoint. The common endpoint is called the vertex of the angle, and rays or line segments are called arms or sides of the angle. Angles measure the amount of turn or rotation between the two rays.
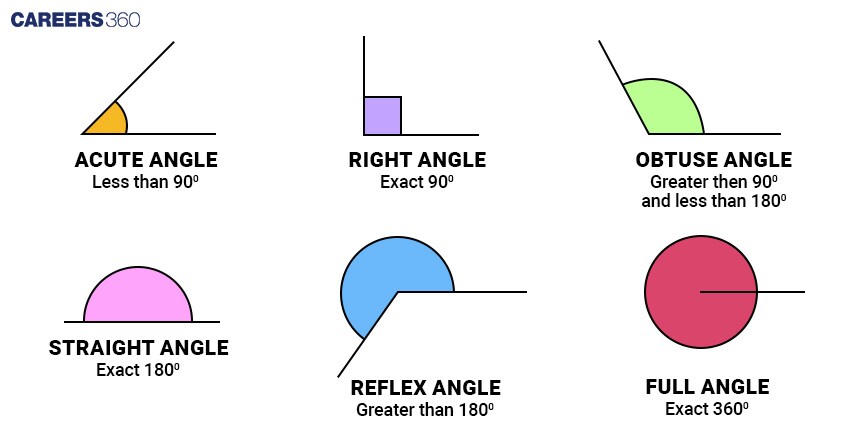
Types of Angles:
-
Acute Angle: An acute angle measures between 0° and 90°.
-
Right Angle: A right angle is exactly equal to 90°.
-
Obtuse Angle: An angle that is greater than 90° but less than 180°.
-
Straight Angle: A straight angle is equal to 180°.
-
Reflex Angle: A reflex angle is greater than 180° but less than 360°.
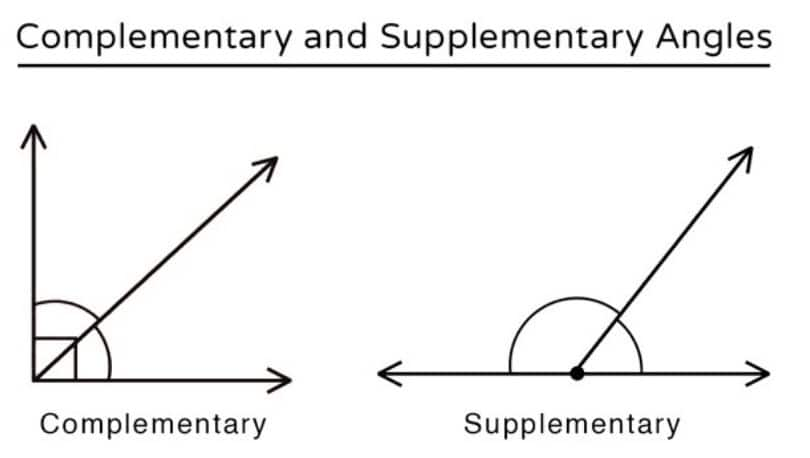
- Complementary Angles (x, y): x + y = 90°
- Supplementary Angles (x, y): x + y = 180°
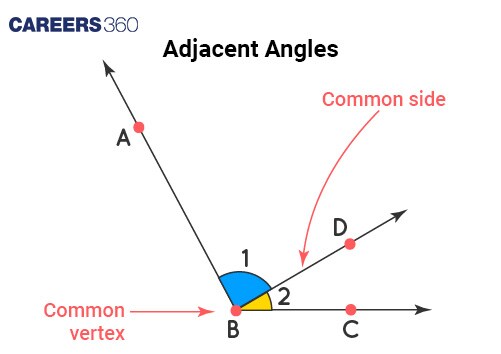
Adjacent Angles:
-
Adjacent angles are two angles that share a common side and a common vertex (corner point) without overlapping.
Linear Pair:
-
A linear pair of angles is formed when two lines intersect. Two angles are considered linear if they are adjacent angles formed by the intersection of two lines. The measure of a straight angle is 180°, so a linear pair of angles must add up to 180°.
Vertically Opposite Angles:
-
Vertically opposite angles are formed when two lines intersect at a point. Vertically opposite angles are always equal.
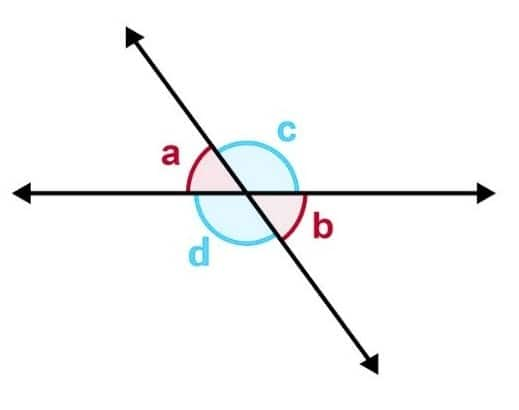
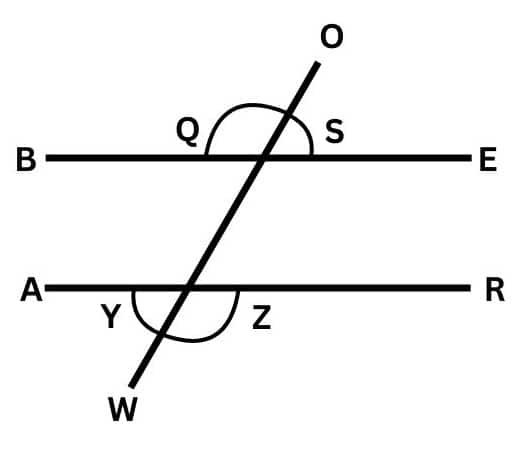
Transversal:
-
A transversal is a line that intersects two or more given lines at distinct points. It is used to create various types of angles, including:
-
Corresponding Angles
-
Alternate Interior Angles
-
Alternate Exterior Angles
-
Interior Angles on the Same Side of the Transversal
-
Approach to Solve Questions of Lines and Angles Class 9
Using these approaches, students can tackle the Lines and Angles Class 9 Chapter 6 Question Answers with greater confidence.
1. Understand different types of angles: Acute, obtuse, straight, reflex, and right angles need revision as a starting point to understand angle relationships in lines.
2. Learn angle pair relationships: Students need to understand complementary angles along with supplementary angles, whereas adjacent angles, linear pairs and vertically opposite angles are necessary for solving angle problems.
3. Know the angle properties of intersecting lines: When two lines intersect, the resulting vertically opposite angles will always be equal in measure to each other.
4. Apply properties of parallel lines with a transversal: You will discover the required behaviours of alternate interior angles, corresponding angles, and consecutive interior angles in cases where parallel lines intersect with a transversal.
5. Use angle theorems for reasoning and proof: When proving lines parallel, it is essential to use angle theorems, especially the “If two lines are parallel, alternate interior angles are equal” theorem, together with its converse proof.
6. Solve problems step-by-step using angle relationships: The solution of angle-based questions progresses easily through known angle pairs combined with postulates to create exact answers.
NCERT Solutions for Class 9 Mathematics: Chapter-wise
Access all NCERT Class 9 Maths solutions from one place using the links below.
Also, read,
- NCERT Notes Class 9 Maths Chapter 6 Lines and Angles
- NCERT Exemplar Solutions for Class 9 Maths Chapter 6 Lines and Angles
NCERT Books and NCERT Syllabus
Before planning a study schedule, always analyse the latest syllabus. Here are the links to the latest NCERT syllabus and some of the important books that will help students in this cause.
Frequently Asked Questions (FAQs)
This chapter deals with angles formed by intersecting lines, properties of parallel lines, and different types of angles. It helps students understand geometric relationships and solve related proofs.
These lines and angles class 9 NCERT solutions provide clear, step-by-step solutions for textbook problems, making it easier for students to learn proofs, apply properties, and solve questions accurately. Also, this chapter is very important not only for this class but also for higher studies.
Free NCERT Lines and Angles Class 9 solutions are available on various educational websites and e-learning platforms such as Careers360, in both online and PDF formats, covering all exercises with step-by-step explanations.
There are 2 exercises in Maths chapter 6 class 9, consisting of 6 and 5 questions, respectively, covering conceptual problems and proofs on lines and angles.
Interior angles: Angles between the two lines cut by a transversal.
Exterior angles: Angles outside the two lines cut by a transversal.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
