Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 9 Maths Chapter 15 Probability

NCERT Solutions for Class 9 Maths Chapter 15 Probability

Edited By Ramraj Saini | Updated on May 08, 2023 11:36 AM IST

NCERT Solutions for Class 9 Maths Chapter 15 Probability

Probability Class 9 Questions And Answers are provided here. These NCERT solutions are prepared by subject matter experts considering latest CBSE syllabus 2023 which are very helpful for exams as these cover most concepts in details and simple language. Suppose you are doing an experiment of tossing a coin 20 times then each toss is known as a trial and the possible outcomes of a toss are head and tail. If in a toss a tail has occurred we call that an event 'tail has occurred' and vice versa. In these NCERT solutions for class 9 maths chapter 15 Probability is designed to provide you step by step solutions to all such problems.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 15 Probability
  2. Probability Class 9 Questions And Answers PDF Free Download
  3. Probability Class 9 Solutions - Important Formulae And Points
  4. Probability Class 9 NCERT Solutions (Intext Questions and Exercise)
  5. Highlights of NCERT Solutions for Class 9 Maths Chapter 15 Probability
  6. NCERT solutions for class 9 maths - Chapter Wise
  7. NCERT solutions for class 9 - Subject Wise
NCERT Solutions for Class 9 Maths Chapter 15 Probability
NCERT Solutions for Class 9 Maths Chapter 15 Probability

In this NCERT Book chapter probability class 9, there is only one exercise that consists of a total of 13 questions including some activities in. Class 9 maths chapter 15 NCERT solutions is covering every practice problem to help you while preparing for the final examinations. Apart from the probability chapter 15 maths class 9. Here you will get NCERT solutions for class 9 Maths also.

\\The \ empirical \ probability \ P(E) \ of \ an \ event \ E \ happening,\ \\P(E)=\frac{Number \ of \ trials \ in \ which \ the \ event \ happened}{The \ total \ number \ of \ trials}

Also, Read

Probability Class 9 Questions And Answers PDF Free Download

Download PDF

Probability Class 9 Solutions - Important Formulae And Points

Probability (P): Probability is a measure that quantifies the likelihood of an event occurring. It is typically expressed as a ratio.

  • Probability (P(E)) = Number of Favourable Outcomes / Total Number of Outcomes

  • The probability of any event lies between 0 and 1, where 0 represents an impossible event, and 1 represents a certain event.

Trial: A trial is defined as a set of observations of an event in which one or more outcomes are observed. It's essentially one attempt or occurrence of an experiment.

Event: An event is defined as a collection of observations performed to observe an experiment. It represents the specific outcomes or results that are of interest in the context of the experiment or situation.

Free download NCERT Solutions for Class 9 Maths Chapter 15 Probability for CBSE Exam.

Probability Class 9 NCERT Solutions (Intext Questions and Exercise)

Class 9 maths chapter 15 question answer - Exercise 15.1

Q1 In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she batswoman. Find the probability that she did not hit a boundary.

Answer:

From the above question, the data of interest is,

Total Number of balls batswoman played = 30

Number of times batswoman hits a boundary =6

Therefore, we can say,

Number of times batswoman could not hit a boundary =24

P(she did not hit a boundary)

= \frac{Number\: of \:times\: batswoman \:cannot \:hit \:a \:boundary }{Total \:Number \:of \:balls \:batswoman \:played }

=24/30 =0.80

Ans:0.80

Q2 (i) 1500 families with 2 children were selected randomly, and the following data were recorded: Compute the probability of a family, chosen at random, having 2 girls

Number of girls in a family 2 1 0
Number of families 475 814 211

Answer:

From the above question, the data that we can take is,

Total Number of families= 475+814+211 = 1500

Number of families having 2 girls in the family =475

We know:

Empirical (or experimental) probability P(E) of this event can be written as

P(Family, chosen at random has 2 girls) =

\frac{Familes\:with \:2 \:girls}{Total \:number \:of \:Families}

= 475/1500 = 19/60

Q2 (ii) 1500 families with 2 children were selected randomly, and the following data were recorded: Compute the probability of a family, chosen at random, having 1 girl

Number of girls in a family 2 1 0
Number of families 475 814 211

Answer:

From the above question, the data that we can take is,

Total Number of families= 475+814+211 = 1500

Number of families having 1 girl in the family =814

We know:

Empirical (or experimental) probability P(E) of this event can be written as

P(Family, chosen at random has 1 girl) =

\frac{Families\:with\: 1\: girl}{Total\:Number\: of \:families}

= 814/1500 = 407/1500

Q2 (iii) 1500 families with 2 children were selected randomly, and the following data were recorded: Compute the probability of a family, chosen at random, having no girl

Number of girls in a family 2 1 0
Number of families 475 814 211

Answer:

From the above question, the data that we can take is,

Total Number of families= 475+814+211 = 1500

Number of families having no girls in the family =211

We know:

Empirical (or experimental) probability P(E) of this event can be written as

P(Family, chosen at random has no girls) =

\frac{Families\:with\:no\:girl}{Total Number of families}

= 211/1500

Ans:= 211/1500

Q3 Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.

Answer:

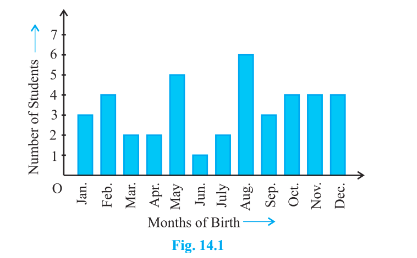
1640672314370

Total no. of students = 40

Total no. of students who all are born in August =6

P( a student of the class was born in August) =6/40

=3/20

Ans : 3/20

Q4 Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:

Outcome

3 Heads

2 Heads

1 Head

0 Head

Frequencies

23

72

77

28

Answer

Total number of times coins tossed = 200

Total number of possible outcomes = 72

Required probability = 72/200 => 9/25

Q5 (i) An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:

Suppose a family is chosen. Find the probability that the family chosen is earning ` Rs. 10000 – Rs.13000 per month and owning exactly 2 vehicles.

Monthly income (in Rs) Vehicles per family
0 1 2 Above 2
Less than 7000 10 160 25 0
7000-10000 0 305 27 2
10000-13000 1 535 29 1
13000-16000 2 469 59 25
16000 or more 1 579 82 88


Answer:

Although it is given that,

Total no. of families= 2400

Let us find this by adding all the cases

= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400

Earning Rs. 10000 – Rs.13000 per month and owning exactly 2 vehicles =29

P(Earning Rs. 10000–Rs.13000 per month and owning exactly 2 vehicles)= P 1

P 1 = 29/2400

Q5 (ii) An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below

Monthly income (in Rs) Vehicles per family
0 1 2 Above 2
Less than 7000 10 160 25 0
7000-10000 0 305 27 2
10000-13000 1 535 29 1
13000-16000 2 469 59 25
16000 or more 1 579 82 88

Suppose a family is chosen. Find the probability that the family chosen is earning Rs.16000 or more per month and owning exactly 1 vehicle.

Answer:

Although it is given that,

Total no. of families= 2400

Let us find by this adding all the cases

= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400

Total no. of families earning Rs.16000 or more per month and owning exactly 1 vehicle = 579

P(earning Rs.16000 or more per month and owning exactly 1 vehicle )= P2

P2 = 579/2400

Q5 (iii) An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:


Monthly income (in Rs) Vehicles per family
0 1 2 Above 2
Less than 7000 10 160 25 0
7000-10000 0 305 27 2
10000-13000 1 535 29 1
13000-16000 2 469 59 25
16000 or more 1 579 82 88

Suppose a family is chosen. Find the probability that the family chose is earning less than Rs. 7000 per month and does not own any vehicle.

Answer:

Although it is given that,

Total no. of families= 2400

Let us find by this adding all the cases

= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400

Total no. of families, those are earning less than Rs. 7000 per month and not having any vehicle = 10

P(earning less than Rs. 7000 per month and does not have any vehicle)= P3

P3 = 10/2400

=1/240

Ans: 1/240

Q5 (iv) An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:

Monthly income (in Rs) Vehicles per family
0 1 2 Above 2
Less than 7000 10 160 25 0
7000-10000 0 305 27 2
10000-13000 1 535 29 1
13000-16000 2 469 59 25
16000 or more 1 579 82 88

Suppose a family is chosen. Find the probability that the family chose is earning `Rs.13000 – 16000 per month and owning more than 2 vehicles.

Answer:

Although it is given that,

Total no. of families= 2400

Let us find by this adding all the cases

= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400

Total number of families,those are earning Rs.13000 – 16000 per month and owning more than 2 vehicles = 25

P(earning Rs.13000 – 16000 per month and owning more than 2 vehicles)= P4

P4 = 25/2400

=1/96

Ans :1/96

Q5 (v) An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:

Monthly income (in Rs) Vehicles per family
0 1 2 Above 2
Less than 7000 10 160 25 0
7000-10000 0 305 27 2
10000-13000 1 535 29 1
13000-16000 2 469 59 25
16000 or more 1 579 82 88

Suppose a family is chosen. Find the probability that the family chosen is owning not more than 1 vehicle.

Answer:

Although it is given that,

Total no. of families= 2400

Let us find by this adding all the cases

= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400

Total number of families owning not more than 1 vehicle= 10+0+1+2+1+160+305+535+469+579 = 2062

Let, P(families owning not more than 1 vehicle)= P5

P5 = 2062/2400

Q6 (i) Refer to Table 14.7, Chapter 14. Find the probability that a student obtained less than 20% in the mathematics test.

Answer:

Marks Number of students
0-20 2
20-30 10
30-40 10
40-50 20
50-60 20
60-70 15
70- above 8
Total 90

From the above question, the data of our interest is:

Total no. of students =90

Total no. of students who obtained less than 20% in the mathematics test= 7

P(student obtained less than 20% in the mathematics test) = 7/90

Ans: 7/90

Q6 (ii) Refer to Table 14.7, Chapter 14. Find the probability that a student obtained marks 60 or above.

Answer:

Marks Number of students
0-20 2
20-30 10
30-40 10
40-50 20
50-60 20
60-70 15
70- above 8
Total 90

From the above question, the data of our interest is:

Total no. of students =90

Total no. of students who obtained marks 60 or above = 15+8 =23

P(a student obtains marks 60 or above) = 23/90

Ans: 23/90

Q7 (i) To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.

Opinion Number of students
like 135
dislike 65

Find the probability that a student is chosen at random likes statistics,

Answer:

From the above question, the data of our interest is:

Total no. of students =135+65 =200

Total no. of students who like statistics = 135

P(students like statistics )= 135/200 =27/40

Ans: 27/40

Q7 (ii) To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.

Opinion Number of students
like 135
dislike 65

Find the probability that a student chosen at random does not like it.

Answer:

From the above question, the data of our interest is:

Total no. of students =135+65=200

Total no. of students who do not like it.= 65

P(a student does not like it) = 65/200

= 13/40

Ans: 13/40

Q8 (i) Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives less than 7 km from her place of work?

Answer:

The distance (in km) of 40 engineers from their residene to their place of work were found as follows:

5 3 10 20 25 11 13 7 12 31
19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3
12 14 2 9 6 15 15 7 6 12

Total no. of engineers = 40

Total no. of engineers who are living less than 7 km from their workplace = 9

Therefore we can say,

P(engineers who are living less than 7 km from their workplace)=

\frac{Total\: no.\: of\: engineers\: who\: are\: living\: less\: than\: 7 km \:from their\: workplace }{Total\:no.\:of\:engineers}

= 9/40

Ans: 9/40

Q8 (ii) Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives more than or equal to 7 km from her place of work?

Answer:

The distance (in km) of 40 engineers from their residene to their place of work were found as follows:

5 3 10 20 25 11 13 7 12 31
19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3
12 14 2 9 6 15 15 7 6 12

Total no. of engineers = 40

Total no. of engineers who are living less than 7 km from their workplace = 31

Therefore we can say,

P(engineers who are living more than or equal to 7 km from their workplace)=31/40

Ans: 31/40

Q8 (iii) Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives within 1/2 km from her place of work?

Answer:

The distance (in km) of 40 engineers from their residene to their place of work were found as follows:

5 3 10 20 25 11 13 7 12 31
19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3
12 14 2 9 6 15 15 7 6 12

Hey, don't you think its too simple:

Well, there is no such engineer whose distance between residence and place of work is less than 1/2 km

Therefore,

engineer whose distance between residence and place of work is less than 1/2 km =0

P(engineer whose distance between residence and place of work is less than 1/2 km) = 0

Ans: 0

Q9 Activity : Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.

Answer:

This activity can be taken as a general problem:

Assumption:

Let the frequency of two-wheelers = x

Let the frequency of three-wheelers = y

Let the frequency of four-wheelers = z

Total no. of vehicles= x+y+z

therefore,

P(anyone vehicle out of the total vehicles I have observed is a two-wheeler) =

\frac{x}{x+y+z}


Q10 Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.

Answer:

This activity can be taken as a general problem:

Well, we know the divisibility by 3 is when the sum of all the digits is divisible by 3

So,

The student will write the number between 100-999

There are 900 3 - digit numbers, which are 100, 101, 102, 103, ..., 999.

The first 3-digit numbers that are exactly divisible by 3 is 102, 105, ..... 999

total numbers which are divisible by 3 = 300

P(the sum of all the digits is divisible by 3) = 300/900

=1/3

Ans: 1/3

Q11 Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.

Answer:

From the above question, the data of our interest is:

Total no. of bags = 11

Total no. of bags that contain more than 5 kg flour = 7

P(Bag contain more than 5 kg flour) = 7/11

Ans: 7/11

Q12 In Q.5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulfur dioxide in the air in parts per million of a certain city for30 days. Using this table, find the probability of the concentration of sulfur dioxide in the interval 0.12 - 0.16 on any of these days.

Answer:

The data is representing the concentration of sulfur dioxide in the air in parts per million (ppm) of a city. The data obtained for a month of 30 days is as follows:

0.03 0.08 0.08 0.09 0.04 0.17
0.16 0.05 0.02 0.06 0.18 0.20
0.11 0.08 0.12 0.13 0.22 0.07
0.08 0.01 0.10 0.06 0.09 0.18
0.11 0.07 0.05 0.07 0.01 0.04

Total no. of days =30

No. of days in which Conc. of sulfur dioxide in the interval 0.12 - 0.16 = 2

P(Conc. of sulphur dioxide in the interval 0.12 - 0.16) =2/30

Ans: 1/15

Q13 In Q.1, Exercise 14.2, you were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.

Answer:

The below-written data is representing the blood groups of 30 students study in class VIII.
A, B, O, O, B, A, O, O, AB, O, A, O, B, A, O
A, AB, O, A, A, B, A, B, O, O, O, AB, B, A, O

Total no. of students = 30

Total no. of students of this class who has blood group AB =3

P(Student of this class has blood group AB)= 3/30 => 1/10

Ans: 1/10

Highlights of NCERT Solutions for Class 9 Maths Chapter 15 Probability

The Class 9 maths chapter 15 NCERT solutions, which focuses on Probability, has several noteworthy features.

  • The information contained within these solutions is authentic, straightforward, and easy to comprehend.
  • They provide answers to all the questions found in the exercise at the conclusion of the chapter, as well as alternative methods for solving examples presented throughout.
  • These solutions were created by Careers360 Mathematics experts who conducted extensive research on each topic.
  • As a result, students can depend on these solutions to prepare for their Class 9 Maths exams, as they include shortcut methods, tips, and tricks that simplify the process of solving complex questions.

if students are interested in class 9 maths ch 15 question answer can access the following link.

Probability Class 9 Exercise 15.1

NCERT solutions for class 9 maths - Chapter Wise

Chapter No. Chapter Name
Chapter 1 Number Systems
Chapter 2 Polynomials
Chapter 3 Coordinate Geometry
Chapter 4 Linear Equations In Two Variables
Chapter 5 Introduction to Euclid's Geometry
Chapter 6 Lines And Angles
Chapter 7 Triangles
Chapter 8 Quadrilaterals
Chapter 9 Areas of Parallelograms and Triangles
Chapter 10 Circles
Chapter 11 Constructions
Chapter 12 Heron’s Formula
Chapter 13 Surface Area and Volumes
Chapter 14 Statistics
Chapter 15 NCERT solutions for class 9 maths chapter 15 Probability

NCERT solutions for class 9 - Subject Wise

NCERT Solutions for Class 9 Maths
NCERT Solutions for Class 9 Science

How to use NCERT solutions for class 9 maths chapter 15 Probability?

  • Try to understand the concept of this chapter using the theory given in the NCERT textbook.
  • Connect the concepts to real-life problems.
  • Go through some examples to understand the way of solving a problem.
  • Practice the questions given in the practice exercises.
  • During the practice, you can use NCERT solutions for class 9 maths chapter 15 Probability as an assistant.

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Question (FAQs)

1. What are the important topics in Maths chapter 15 class 9 Probability?

Basic probability, independent events, and conditional probability are the important topics of this chapter. students should prioritize important topics, and scheduling time according to priority will give aces to aspirants and help to excel in exams. For ease you can study probability class 9 pdf both online and offline mode.

2. How many chapters are there in CBSE class 9 maths ?

There are 15 chapters  in starting from numbers systems to probability in the CBSE class 9 maths. students can find a list in NCERT syllabus as well as in NCERT Book.

3. What is the meaning of probability according to ch 15 maths class 9?

As per the NCERT Solutions for Class 9 Maths Chapter 15, Probability refers to the likelihood of an event occurring and is considered a mathematical discipline that deals with such random events. The probability of an event is expressed as a value ranging from zero to one. The study of probability in mathematics allows us to predict the likelihood of various events occurring.

4. Where can I find the complete probability class 9 NCERT solutions ?

Here you will get the detailed NCERT solutions for class 9 maths  by clicking on the link. you can practice these class 9 probability NCERT solutions to get indepth understanding of the concepts that are essential for exams.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:15 July,2024 - 14 August,2024

Maharashtra School Leaving Certificate Examination

Exam Date:16 July,2024 - 30 July,2024

Maharashtra Higher Secondary School Certificate Examination

Exam Date:16 July,2024 - 08 August,2024

National Institute of Open Schooling 12th Examination

Late Fee Application Date:22 July,2024 - 31 July,2024

National Institute of Open Schooling 10th examination

Late Fee Application Date:22 July,2024 - 31 July,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Exam 2024 Registrations
PTE Exam 2024 Registrations
Apply

Register now for PTE & Save 5% on English Proficiency Tests with ApplyShop Gift Cards

View All Application Forms
News and Notifications
President Droupadi Murmu takes up role of teacher for school students, stresses environment conservation
Arunachal Pradesh government to close down zero enrolment schools: Education minister
Economic Survey Highlights: India is spending just 2.7% of GDP on education
Rain wreaks havoc in Nilgiris district, schools closed
MoE announces celebration of Shiksha Saptah from July 22 to 28, marks 4th anniversary of NEP 2020
Student stabs schoolmate in Delhi's Jahangirpuri, sent to juvenile home
Karnataka to provide eggs six days a week to students in government and aided schools
Back to top