NCERT Solutions for Class 9 Maths Chapter 11 Constructions

Edited By Ramraj Saini | Updated on May 11, 2023 03:49 PM IST

NCERT Solutions for Class 9 Maths Chapter 11 Constructions

NCERT solutions for class 9 maths chapter 11 Constructions are discusses in this article. These NCERT solutions are prepared by expert team at Careers360 considering the latest CBSE syllabus 2023-24. These solutions are designed in simple, easy to understand and comprehensive way to help students. The chapter construction class 9 deals with the construction of certain angles and also triangles in certain conditions.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Chapter 11 Constructions
Constructions Class 9 Questions And Answers PDF Free Download
Constructions Class 9 Solutions - Important Points
Constructions Class 9 NCERT Solutions (Intext Questions and Exercise)
Summary Of Class 9 Constructions NCERT Solutions
NCERT solutions for class 9 maths chapter wise
NCERT solutions for class 9 subject wise
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 9 Maths Chapter 11 Constructions

When there is any construction project to start, then the first step to initiate that project is the planning and drawing. Geometrical constructions have their own line of study. If you want to pursue your career in this domain then the higher study related to this can be civil engineering and architecture. In this construction class 9 NCERT book chapter, there are 2 exercises having a total of 14 questions. Constructions Class 9 Questions And Answers have an in-depth solution to each and every question present in the practice exercises. For 360-degree help in your school examination preparation, you can use NCERT solutions for class 9 Maths.

Also read:

Constructions Class 9 Questions And Answers PDF Free Download

Download PDF

Constructions Class 9 Solutions - Important Points

Construction of Bisector of a Line Segment:

This construction task involves finding the midpoint of a given line segment. To construct the bisector, draw two congruent arcs from each endpoint of the segment. Where these arcs intersect is the midpoint of the line segment.

Construction of Bisector of a Given Angle:

Place the compass at the vertex of the angle.
Draw an arc that intersects both arms of the angle.
Repeat the process from the other arm of the angle.
The point where the two arcs intersect is the angle bisector.

Construction of an Equilateral Triangle:

Draw a line segment to represent one side of the equilateral triangle.
Place the compass at one endpoint of the line segment and draw an arc.
Repeat the process from the other endpoint.
Where the two arcs intersect, connect it to the endpoints of the line segment. This forms an equilateral triangle.

Construction of a Triangle Given Its Base, Sum of the Other Two Sides, and One Base Angle:

This construction involves constructing a triangle when you know one of its base angles, the length of the base, and the sum of the lengths of the other two sides. Specific construction steps would depend on the given measurements.

Construction of a Triangle Given Its Base, Difference of the Other Two Sides, and One Base Angle:

Similar to the previous construction, this involves constructing a triangle when you know one of its base angles, the length of the base, and the difference between the lengths of the other two sides. Specific construction steps would depend on the given measurements.

Construction of a Triangle of Given Perimeter and Two Base Angles:

This construction task involves constructing a triangle with specified base angles and a given perimeter. Specific construction steps would depend on the given measurements.

Free download NCERT Solutions for Class 9 Maths Chapter 11 Constructions for CBSE Exam.

Constructions Class 9 NCERT Solutions (Intext Questions and Exercise)

Class 9 maths chapter 11 question answer - Exercise: 11.1

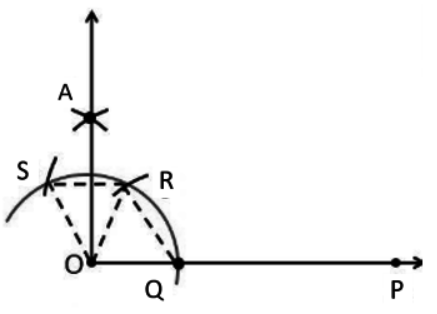
Q1 Construct an angle of 90 ^o at the initial point of a given ray and justify the construction.

Answer:

The steps of construction to follow:

Step 1: Draw a ray OP.

Then, take O as the centre and any radius draw an arc cutting OP at Q.

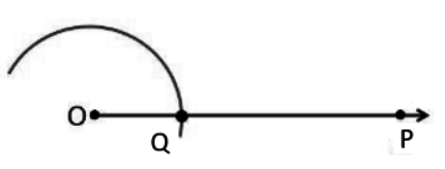
1640600746099

Step 2: Now, taking Q as the centre and with the same radius as before draw an arc cutting the previous arc at R. Repeat the process with R to cut the previous arc at S.

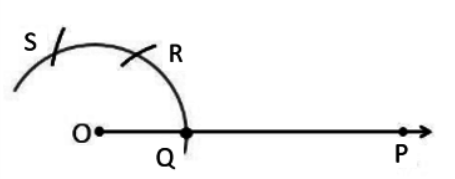
1640600957166

Step 3: Take R and S as centre draw the arc of radius more than the half of RS and draw two arcs intersecting at A. Then, join OA.

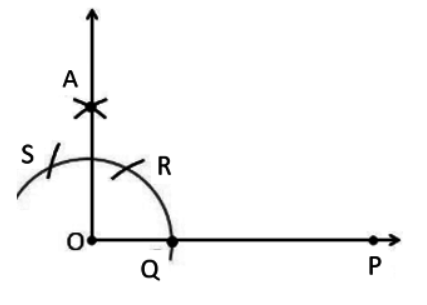
1640600972011

Hence, $\angle POA = 90^{\circ }$ .

Justification:

We need to justify, $\angle POA = 90^{\circ }$

So, join OR and OS and RQ. we obtain

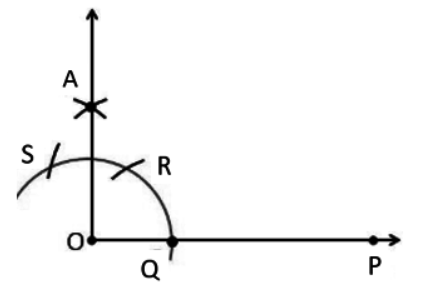
1640600984472

By construction OQ = OS = QR.

So, $\triangle ROQ$ is an equilateral triangle. Similarly $\triangle SOR$ is an equilateral triangle.

So, $\angle SOR = 60^{\circ}$

Now, $\angle ROQ = 60^{\circ}$ that means $\angle ROP = 60^{\circ}$ .

Then, join AS and AR:

1640601001877

Now, in triangles OSA and ORA:

$SR = SR$ (common)

$AS = AR$ (Radii of same arcs)

$OS = OR$ (radii of the same arcs)

So, $\angle SOA = \angle ROA = \frac{1}{2}\angle SOR$

Therefore, $\angle ROA = 30^{\circ}$

and $\angle POA = \angle ROA+\angle POR = 30^{\circ} +60^{\circ} =90^{\circ}$

Hence, justified.

Q2 Construct an angle of 45 ^o at the initial point of a given ray and justify the construction.

Answer:

The steps of construction to follow:

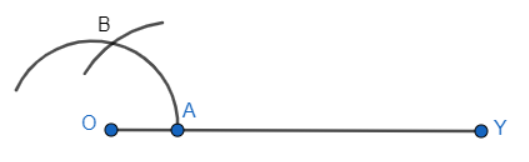
Step 1: Draw a ray OY.

Then, take O as the centre and any radius, mark a point A on the arc ABC.

1640601062706

Step 2: Now, taking A as the centre and the same radius, mark a point B on the arc ABC.

1640601050776

Step 3: Take B as a centre and the same radius, mark a point C on the arc ABC.

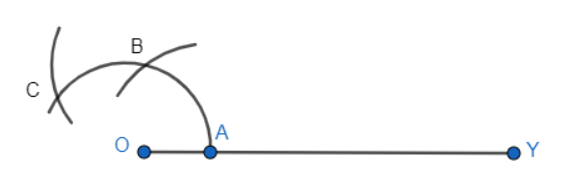
1640601072959

Step 4: Now, taking C and B as centre one by one, draw an arc from each centre intersecting each other at a point X.

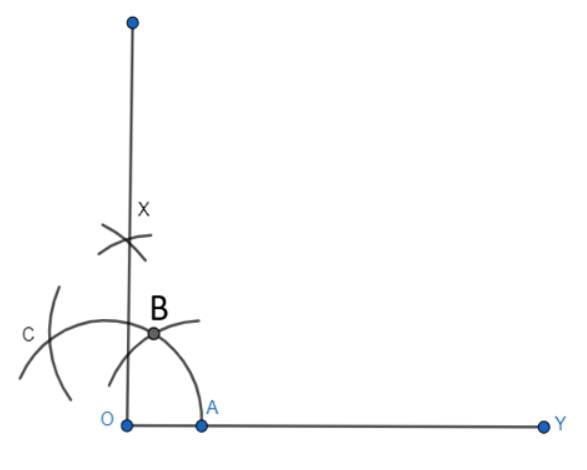
1640601086817

Step 5: X and O are joined and a ray making an angle $90^{\circ}$ with OY is formed.

Let the arc AC touches OX at E

Step 6: With A and E as centres, 2 arcs are marked intersecting each other at D and the bisector of angle XOY is drawn.

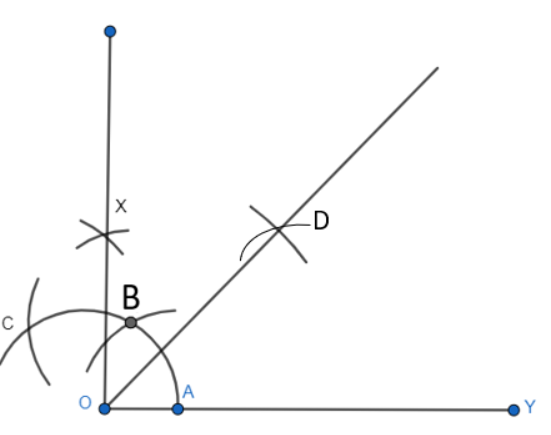
1640601100159

Justification:

By construction we have,

$\angle XOY = 90^{\circ}$

We constructed the bisector of $\angle XOY$ as $\angle DOY$

Thus,

$\angle DOY = \frac{1}{2}\angle XOY = \frac{1}{2}\times90^{\circ} = 45^{\circ}$

Q3 (i) Construct the angles of the following measurements: 30 ^o

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601126922

Step 2: Now, take A as a center and take any radius, then draw an arc AB cutting OY at A.

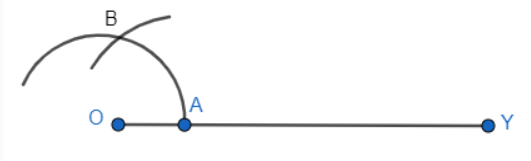
1640601139457

Step 3: Take A and B as centres, draw 2 arcs are marked intersecting each other at X and hence, the bisector of $30^{\circ}$ is constructed.

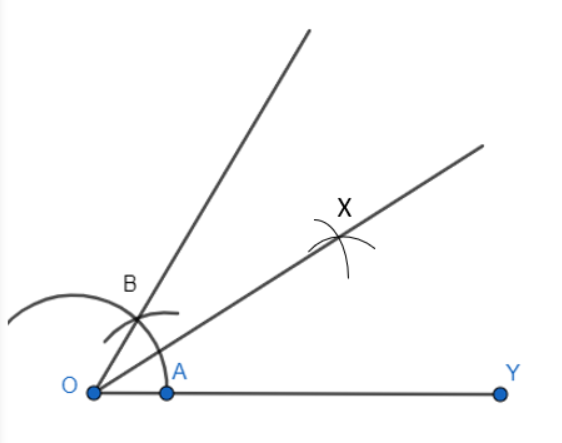
1640601151573

Thus, $\angle XOY$ is the required angle.

Q3.Construct the angles of the following measurements: (i) 30o
Edit Q

Q3 (ii) Construct the angles of the following measurements: $22\frac{1}{2}\degree$

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601174811

Step 2: Now, take A as a centre and take any radius, then mark a point B on the arc

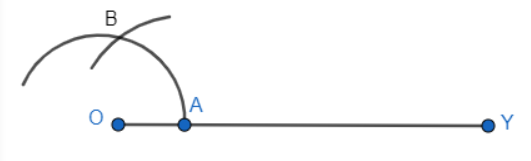
1640601184856

Step 3: Take B as a centre with the same radius, mark a point C on the arc ABC.

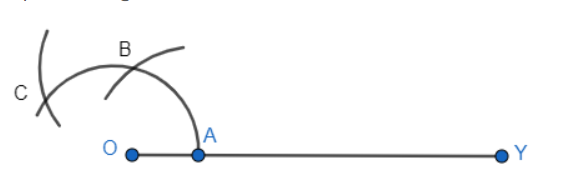
1640601195448

Step 4: Now, taking B and C as centres simultaneously, then draw an arc from each centre intersecting each other at a point X. Then join X and O and a ray making an angle with OY is formed.

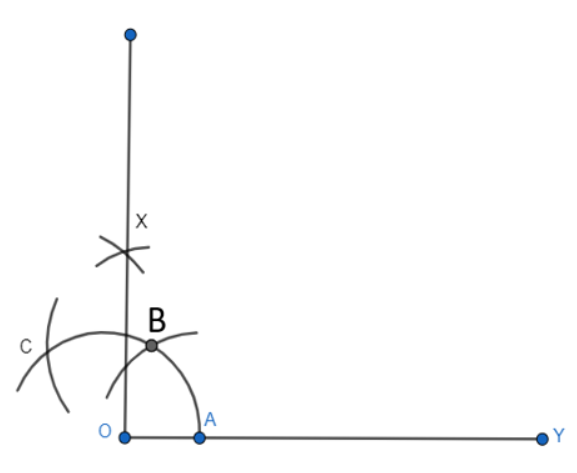
1640601206833

Let the arc AC touches OX at E

Step 5: Now, with A and E as centres, mark 2 arcs which intersect each other at D and we obtain the bisector of the angle $XOY$ .

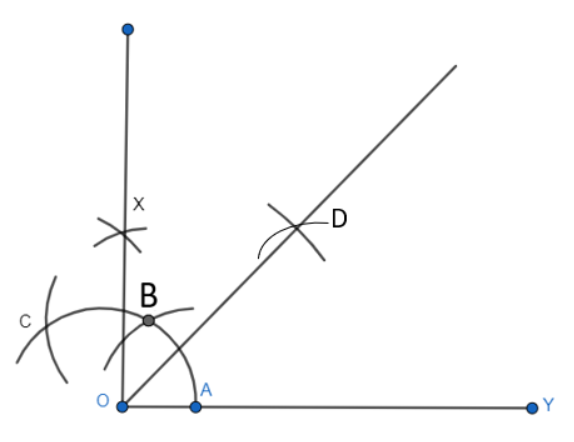
1640601218774

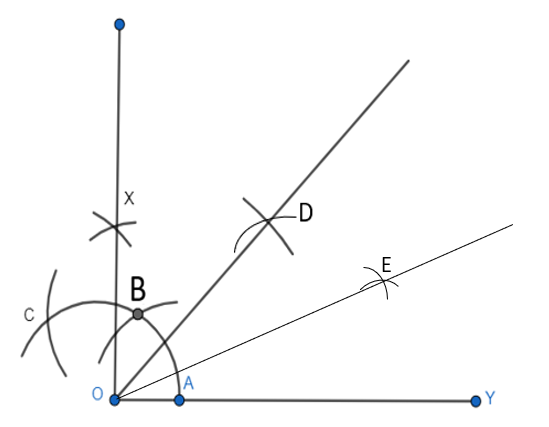
1640601229663

Q3 (iii) Construct the angles of the following measurements: 15 ^o

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601261458

Step 2: Now, take A as a centre and take any radius, draw an arc AB which cuts OY at A.

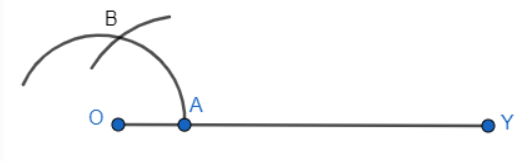
1640601272131

Step 3: Take A and B as a centre, then mark 2 arcs which intersect each other at X and Hence, the bisector is constructed of $30^{\circ}$ .

Step 4: Now, with A and E as centres, mark 2 arcs which intersect each other at D and we obtain the bisector of the angle $XOY$ .

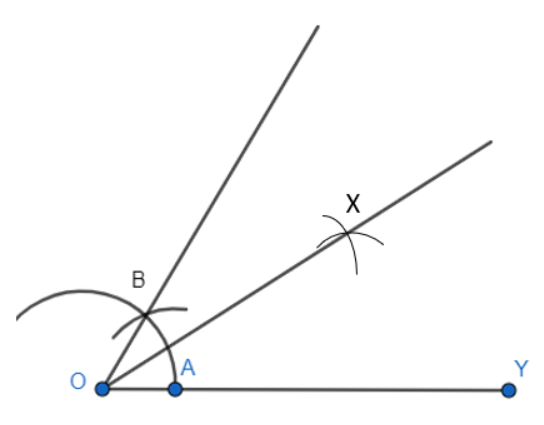
1640601288755

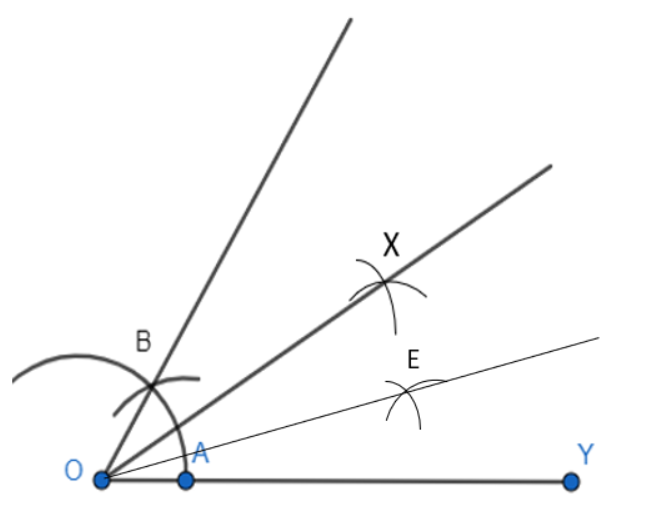
1640601299418

Thus, the angle of $15^{\circ}$ is obtained which is $\angle EOY.$

Q4 (i) Construct the following angles and verify by measuring them by a protractor: 75 ^o

Answer:

Steps to construction to follow:

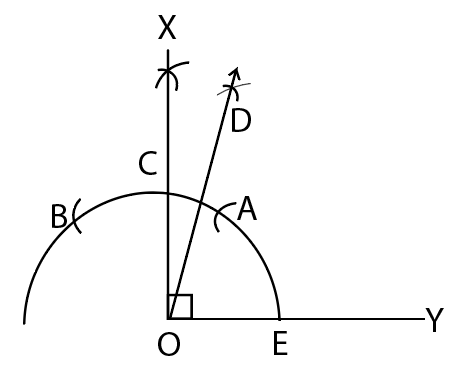
1640601336495

Step 1: Draw a ray OY.

Step 2: Now, taking O as the centre draw an arc ABC.

Step 3: On taking A as a centre, draw two arcs B and C on the arc ABC.

Step 4: Now, taking B and C as centres, arcs are made to intersect at point E and the $\angle EOY = 90^{\circ}$ is constructed.

Step 5: Taking A and C as centres, arcs are made to intersect at D.

Step 6: Now, join OD and hence, $\angle DOY = 75^{\circ}$ is constructed.

Hence, $\angle DOY$ is the required angle.

Q4 (ii) Construct the following angles and verify by measuring them by a protractor: 105 ^o

Answer:

The steps of construction to be followed:

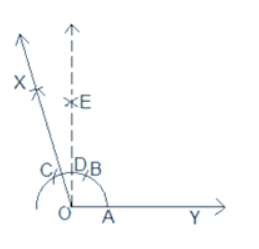
1640601361664

Step 1: Draw a ray OY.

Step 2: Then, taking O as a centre, draw an arc ABC.

Step 3: Now, with A as a centre, draw two arcs B and C which are made on the arc ABC.

Step 4: Taking B and C as centres simultaneously, arcs are made to intersect at E and $\angle EOY =90^{\circ}$ is constructed.

Step 5: With B and C as centres, arcs are made to intersect at X.

Step 6: Join the OX and we get $\angle XOY =105^{\circ}$ is constructed.

Thus, the angle $XOY$ is $105^{\circ}.$

Q4 (iii) Construct the following angles and verify by measuring them by a protractor: 135 ^o

Answer:

The steps of construction to be followed:

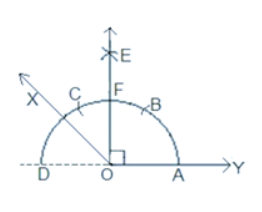
1640601385098

Step 1: Draw a ray DY.

Step 2: Draw an arc ACD with O as a center.

Step 3: Now, with A as a centre, draw two arcs B and C on the arc ACD.

Step 4: Taking B and C as centres, arcs are made to intersect at E and the angle formed is $\angle EOY = 90^{\circ}$ .

Step 5: Take F and D as centres, draw arcs to intersect at point X or the bisector of angle EOD is made.

Step 6: Join OX and the $\angle XOY = 135^{\circ}$ is made.

Hence, the angle required $\angle XOY$ is $135^{\circ}$ .

Q5 Construct an equilateral triangle, given its side and justify the construction.

Answer:

The following steps to make an equilateral triangle:

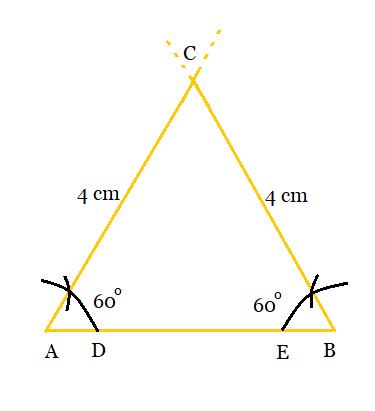
1640601397009

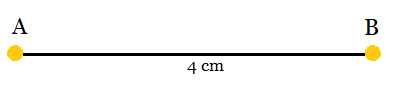
Step 1: Draw a line segment AB = 4 cm.

1640601407591

Step 2: With A and B as centres, make two arcs in the line segment AB. Mark it as D and E respectively.

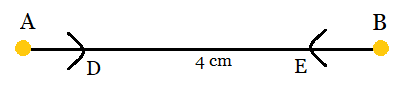
1640601419076

Step 3: Now, with D and E as centres, make the two arcs cutting the previous arcs respectively, and forming an angle of $60^{\circ }$ each.

Step 4: Extend the lines of A and B until they intersect each other at point C.

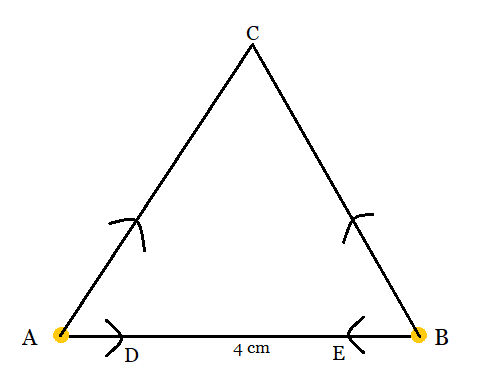
1640601431722

Hence, triangle constructed is ABC which is equilateral.

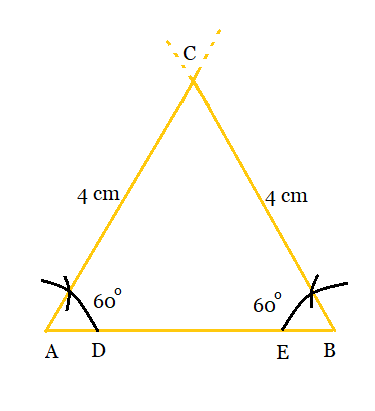
1640601440890

Now, Justification ;

Since the angles constructed are of $60^{\circ }$ each, so the third angle will also be $60^{\circ }$ .

$\left [ \because The\ sum\ of\ all\ angles\ of\ triangle = 180^{\circ} \right ]$

Class 9 maths chapter 11 NCERT solutions - Excercise: 11.2

Q1 Construct a triangle ABC in which $BC = 7cm$ , $\angle B = 75\degree$ and $AB + AC = 13 cm$ .

Answer:

The steps of construction are as follows:

Step 1: Draw a line segment BC of 7cm length. Taking the help of protractor make an $\angle XBC = 75^{\circ}$ .

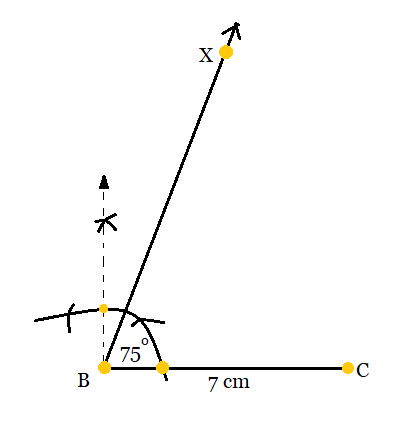
1640601458338

Step 2: Now, cut a line segment BD having 13 cm on BX which is $(AB+AC).$

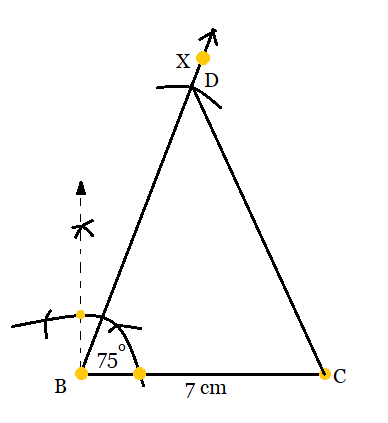
1640601468104

Step 3: Now, join CD.

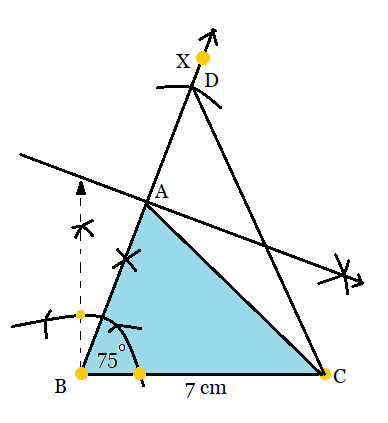
1640601479666

Step 4: Draw a perpendicular bisector of CD to intersect BD at a point A. Join AC. Then ABC is the required triangle

Hence, the required triangle is ABC.

Q2 Construct a triangle ABC in which $BC = 8cm$ , $\angle B = 45\degree$ ° and $AB - AC = 3.5cm$

Answer:

The steps of construction to be followed:

Step 1: Draw a line segment BC = 8cm and make an angle of $45^{\circ}$ at point B i.e., $\angle XBC.$

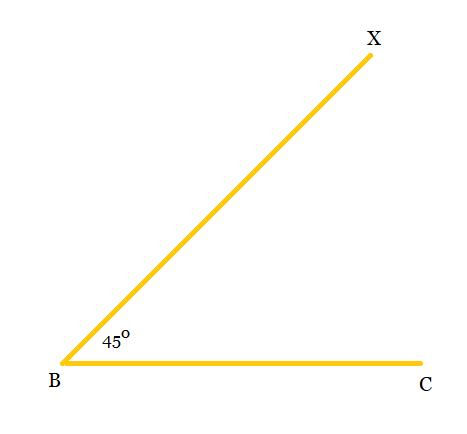
1640601500495

Step 2: Now, cut the line segment BD = 3.5 cm on ray BX. i.e. $(AB-AC)$ .

Step 3: Join CD and draw a perpendicular bisector of CD i.e., PQ.

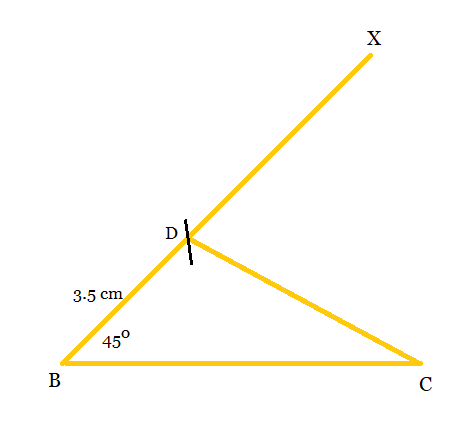
1640601513380

Step 4: Let the perpendicular bisector of CD intersects BX at point A. Then,

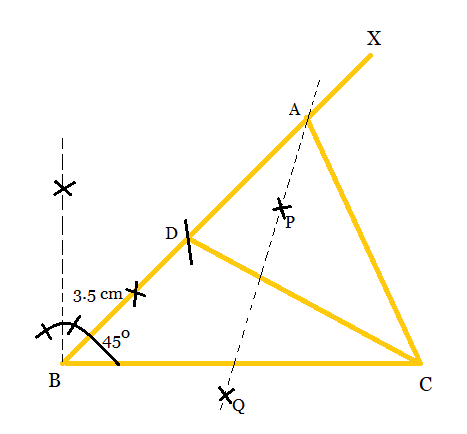
1640601551723

Step 5: Join AC, to get the required triangle $\triangle ABC.$

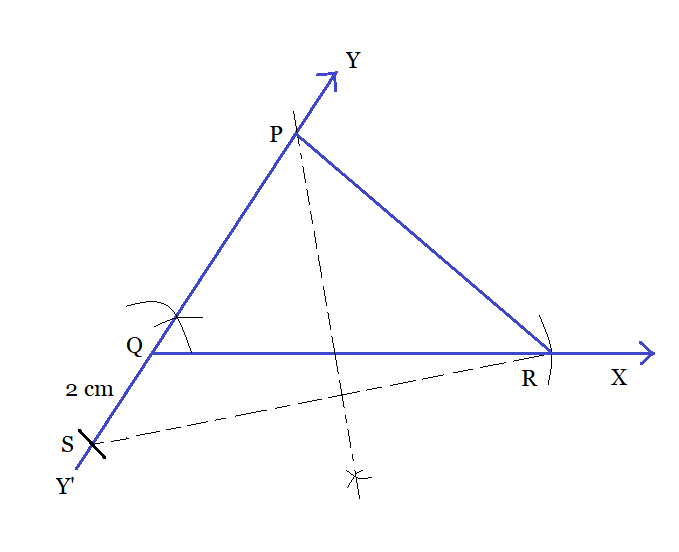
Q3 Construct a triangle PQR in which $QR = 6cm$ , $\angle Q = 60 \degree$ and $PR -PQ = 2cm$ .

Answer:

The steps of construction to be followed:

Step 1: Draw a ray QX and cut off a line segment QR which is equal to 6 cm in length.

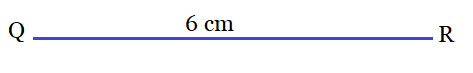
1640601586225

Step 2: With an angle of $60^{\circ}$ with QR, construct a ray QY and extend it to form a line YQY'.

Step 3: Now, cut off a line segment QS equal to 2 cm from QY' and join RS.

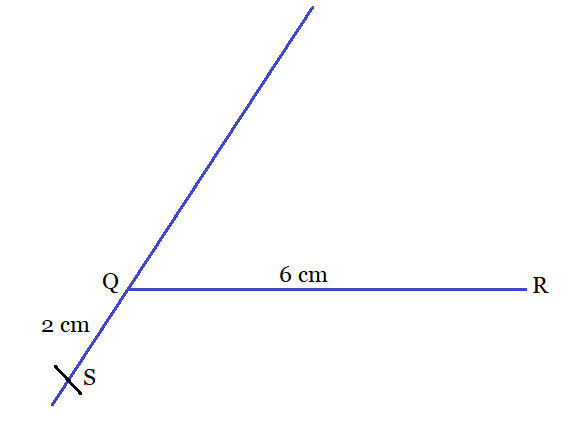
1640601600248

Step 4: Draw a perpendicular bisector of RS which intersects QY at a point P.

Step 5: Join PR to get the required triangle $\triangle PQR.$

1640601611912

Q4 Construct a triangle XYZ in which $\angle Y = 30\degree$ , $\angle Z = 90\degree$ ° and $XY + YZ + ZX = 11 cm$ .

Answer:

The steps of construction to be followed:

Step 1: For given $XY+YZ+ZX = 11 cm$ , a line segment $PQ =11 cm$ is drawn.

Step 2: At points, P and Q angles of $\angle RPQ = 30^{\circ}$ and $\angle SQP =90^{\circ}$ are constructed respectively.

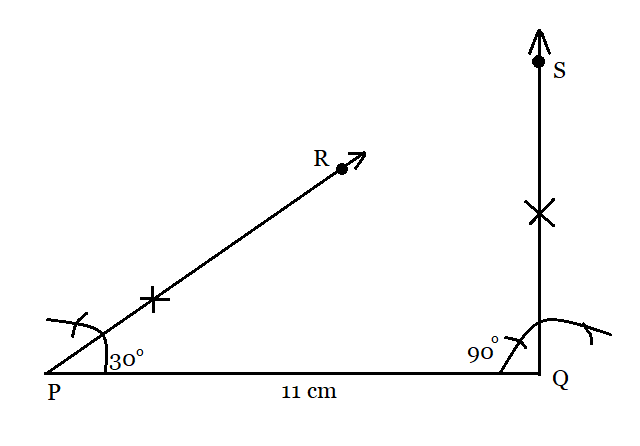
1640601637611

Step 3: Now, bisects the angle RPQ and SQP. The bisectors of these angles intersect each other at a point X.

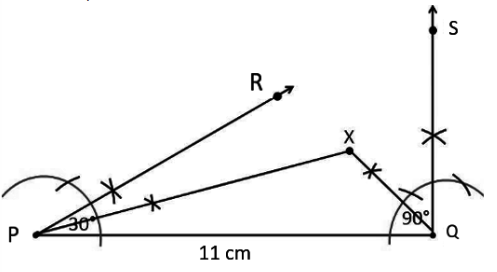
1640601651930

Step 4: Construct the perpendicular bisector of PX and QX, name them as TU and WV respectively.

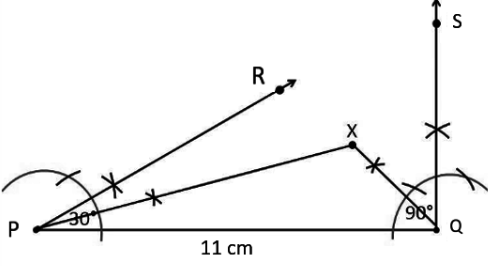
1640601673964

Step 5: Let the bisector TU intersect PQ at Y and bisector WV intersect PQ at Z. Then XY and ZY are joined.

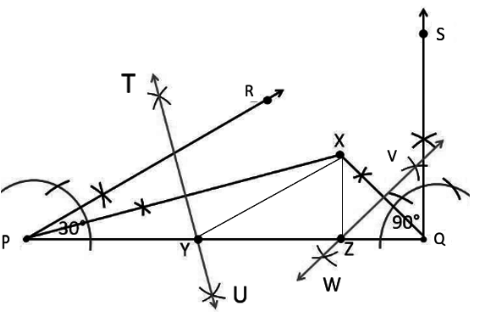
1640601685870

Therefore, $\triangle XYZ$ is the required triangle.

Q5 Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.

Answer:

The steps of construction to follow:

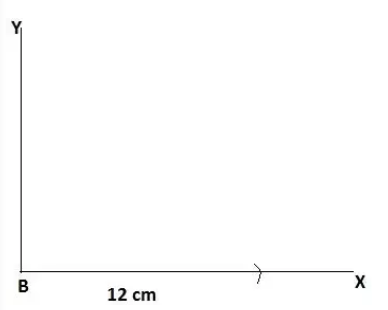
Step 1: Draw a ray BX and Cut off a line segment $BC=12cm$ from the ray.

1640601714690

Step 2: Now, construct an angle $\angle XBY = 90^{\circ}$ .

1640601724612

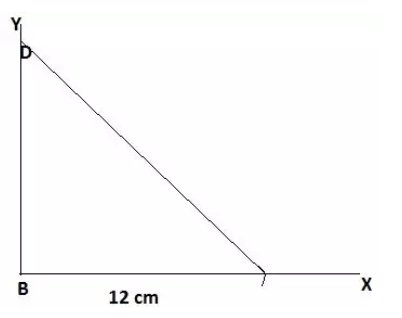
Step 3: Cut off a line segment BD of length 18 cm on BY. Then join the CD.

1640601736897

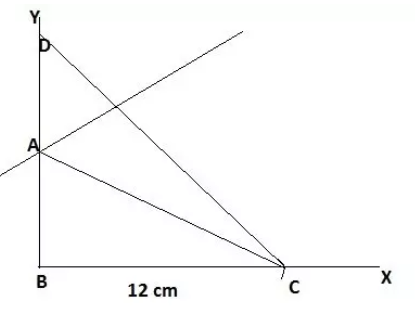
Step 4: Now, construct a perpendicular bisector of CD which intersects BD at A and AC is joined.

1640601751004

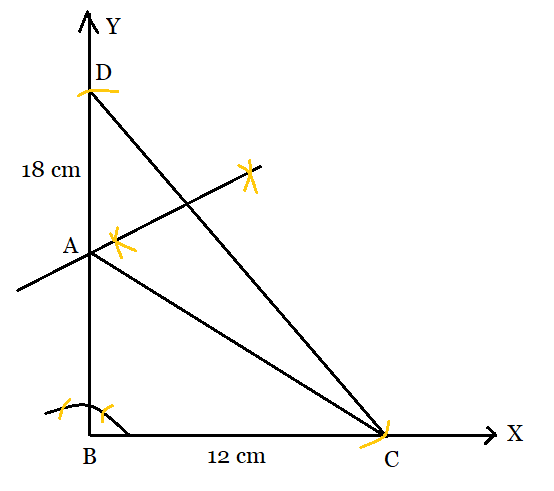
1640601761290

Thus, the constructed triangle is ABC.

Summary Of Class 9 Constructions NCERT Solutions

Constructions in geometry are the methods of drawing geometric shapes and figures using a straightedge and a compass.
Some basic constructions include drawing a line parallel to a given line through a given point, bisecting a given line segment, constructing the perpendicular bisector of a given line segment, and drawing an angle of a given measure.
To construct a perpendicular bisector of a given line segment AB, we draw a circle with A and B as its endpoints, then draw another circle with the same radius and center at B. The intersection of the two circles gives the midpoint M of AB. The line passing through M and perpendicular to AB is the perpendicular bisector of AB.
To construct an angle of a given measure, we first draw a ray with an endpoint O. We then place the compass at O and draw an arc intersecting the ray at point A. We then draw another arc with the same radius and center at A. We mark the point of intersection of these two arcs as B. The angle ∠AOB is the required angle.
Constructions are useful in various fields, such as architecture, engineering, and art.
The accuracy of constructions depends on the precision of the tools used and the skill of the person performing the construction.
The constructions discussed in this chapter are important in higher-level geometry, and they form the basis for several advanced constructions and theorems.

Here students can find class 9 maths ch 11 question answer using exercise link given below.

NCERT solutions for class 9 maths chapter wise

Chapter No.	Chapter Name
Chapter 1	Number Systems
Chapter 2	Polynomials
Chapter 3	Coordinate Geometry
Chapter 4	Linear Equations In Two Variables
Chapter 5	Introduction to Euclid's Geometry
Chapter 6	Lines And Angles
Chapter 7	Triangles
Chapter 8	Quadrilaterals
Chapter 9	Areas of Parallelograms and Triangles
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Heron’s Formula
Chapter 13	Surface Area and Volumes
Chapter 14	Statistics
Chapter 15	Probability

NCERT solutions for class 9 subject wise

NCERT Solutions for Class 9 Maths

NCERT Solutions for Class 9 Science

How to use NCERT solutions for class 9 maths chapter 11 Constructions

Understand the basic construction of angles using the previous class book.
Learn the constructional process of triangles and rectangles.
Go through some solved examples to understand the solutions pattern.
Apply the concepts learned in the practice exercises.
If you feel trouble in solving any problem then take the assistance of NCERT solutions for class 9 maths chapter 11 Constructions.

NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

1. What are the important topics in construction maths chapter 11 class 9 ?

Basic Construction and Construction of triangles are two important topics in this chapter. Students can priorities the important chapters according to the NCERT syllabus and practice them to get good score well in the exam. practicing These NCERT Solutions will help students to command the concepts and provide confidence during the exam which ultimately lead to score well in the exams.

2. Where can I find the complete solutions of chapter 11 maths class 9 ?

Here students can get NCERT solutions for class 9 . these solutions are prepared by expert team at Careers360 conidering the students demand and thus are very beneficial for students. After practicing these solutions and problems you will get in-depth understanding of the concepts.

3. What is the significance of NCERT Solutions for Class 9 Maths Chapter 11 in terms of board exam preparation?

NCERT Solutions for ch 11 maths class 9 are a valuable resource that offers comprehensive information and understanding of every concept, which enables students to solve all types of questions, regardless of their level of difficulty. Consistent practice is crucial to learning and scoring well in Mathematics. Therefore, a wide range of questions, along with their solutions, shortcut techniques, and detailed explanations, are provided to practice any concept thoroughly.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 9 Maths Chapter 11 Constructions

NCERT Solutions for Class 9 Maths Chapter 11 Constructions

Constructions Class 9 Questions And Answers PDF Free Download

Constructions Class 9 Solutions - Important Points

Constructions Class 9 NCERT Solutions (Intext Questions and Exercise)

Summary Of Class 9 Constructions NCERT Solutions

NCERT solutions for class 9 maths chapter wise

NCERT solutions for class 9 subject wise

NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app