Tallentex 2025 - ALLEN's Talent Encouragement Exam
ApplyRegister for Tallentex '25 - One of The Biggest Talent Encouragement Exam
Circles Class 9 Questions And Answers are provided here. These NCERT solutions are prepared by experts at Careers360 considering latest CBSE syllabus 2023. All NCERT problems are discussed in simple, easy to understand and comprehensive way. Thus, these will help students to score well in the exams. Many objects that we come across in our daily life is circular in shape, such as ring, bangle, wheels of the vehicle, clock, etc. NCERT solutions for class 9 maths chapter 10 Circles will help in solving all problems given in the book related to circular shapes.

The circle is an integral part of unit geometry. A circle divides the plane in which the circle lies into three parts as shown in figure 1, which are the interior of the circle, the exterior of the circle and the circle. In this particular chapter, you will learn the proof of theorems and problems based on those theorems. NCERT class 9 maths chapter 10 question answer are designed in such a way that a student can fetch 100% marks in a particular question. Here you will get NCERT solutions for class 9 Maths also.
Also Read :
Concentric Circles: Concentric circles are circles that share the same centre but have different radii.
Arc: An arc of a circle is a continuous portion of the circle.
Chord of a Circle: The chord of a circle is a line segment that connects any two points on the circle.
>> Some Important Properties Of Circle Chords
The diameter of a circle is a chord that passes through its centre.
A circle's diameter divides it into two equal arcs, forming a semicircle.
Congruent arcs have the same degree measure.
Equal arcs have associated chords of the same length.
A perpendicular drawn from the centre to a chord bisects the chord, and vice versa.
Three non-collinear points define one and only one circle.
Chords equidistant from the centre are equal in length.
The line connecting the centres of two intersecting circles and their common chord are perpendicular.
The central angle of an arc is twice the angle it subtends on the circumference.
Any two angles in the same circle segment are equal.
Equal chords of a circle create equal central angles at the centre.
The larger chord of a circle is closer to the centre than the smaller chord.
A semicircle contains a right angle.
Equal chords in a circle subtend equal angles at the centre.
Cyclic Quadrilateral:
A quadrilateral is termed cyclic if all of its vertices lie on the circumference of a circle.
The sum of opposite angles in a cyclic quadrilateral is 180°, and vice versa.
An exterior angle of a cyclic quadrilateral is equal to its opposite inner angle.
Tangent and Radius:
The tangent and radius of a circle intersect at a right angle.
Free download NCERT Solutions for Class 9 Maths Chapter 10 Circles for CBSE Exam.
Class 9 maths chapter 10 NCERT solutions - Exercise: 10.1
Fill in the blanks:
Q1 (i) The centre of a circle lies in _____________ of the circle. (exterior/ interior)
Answer:
The centre of a circle lies in the interior of the circle.
Fill in the blanks:
Answer:
A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle.
Fill in the blanks:
Q1 (iii) The longest chord of a circle is a ___________ of the circle.
Answer:
The longest chord of a circle is a diameter of the circle.
Fill in the blanks:
Q1 (iv) An arc is a ________________ when its ends are the ends of a diameter.
Answer:
An arc is a semi- circle when its ends are the ends of a diameter.
Fill in the blanks:
Q1 (v) Segment of a circle is the region between an arc and ________________ of the circle.
Answer:
Segment of a circle is the region between an arc and chord of the circle.
Fill in the blanks:
Q1 (vi) A circle divides the plane, on which it lies, in _______________ parts.
Answer:
A circle divides the plane, on which it lies, in two parts.
Write True or False: Give reasons for your answers.
Q2 (i) Line segment joining the centre to any point on the circle is a radius of the circle.
Answer:
True. As line segment joining the centre to any point on the circle is a radius of the circle.
Write True or False: Give reasons for your answers.
Q2 (ii) A circle has only finite number of equal chords.
Answer:
False . As a circle has infinite number of equal chords.
Write True or False: Give reasons for your answers.
Q2 (iii) If a circle is divided into three equal arcs, each is a major arc.
Answer:
False. If a circle is divided into three equal arcs, each arc makes angle of 120 degrees whereas major arc makes angle greater than 180 degree at centre.
Write True or False: Give reasons for your answers.
Q2 (iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Answer:
True.A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Write True or False: Give reasons for your answers.
Q2 (v) Sector is the region between the chord and its corresponding arc.
Answer:
False. As the sector is the region between the radii and arc.
Write True or False: Give reasons for your answers.
Q2 (vi) A circle is a plane figure.
Answer:
True. A circle is a plane figure.
Circles class 9 NCERT solutions - Exercise: 10.2
Answer:
Given: The two circles are congruent if they have the same radii.
To prove: The equal chords of congruent circles subtend equal angles at their centres i.e. BAC=
QPR
Proof :
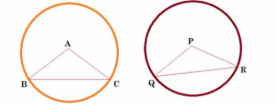
In ABC and
PQR,
BC = QR (Given)
AB = PQ (Radii of congruent circle)
AC = PR (Radii of congruent circle)
Thus, ABC
PQR (By SSS rule)
BAC=
QPR (CPCT)
Answer:
Given : chords of congruent circles subtend equal angles at their centres,
To prove : BC = QR
Proof : 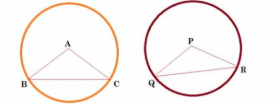
In ABC and
PQR,
BAC=
QPR (Given)
AB = PQ (Radii of congruent circle)
AC = PR (Radii of congruent circle)
Thus, ABC
PQR (By SAS rule)
BC = QR (CPCT)
Class 9 circles ncert solutions - Exercise: 10.3
Answer:

In (i) we do not have any common point.
In (ii) we have 1 common point.
In (iii) we have 1 common point.
In (iv) we have 2 common points.
The maximum number of common points is 2.
Q2 Suppose you are given a circle. Give a construction to find its centre.
Answer:
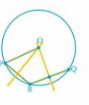
Given : Points P,Q,R lies on circle.
Construction :
1. Join PR and QR
2. Draw perpendicular bisector of PR and QR which intersects at point O.
3. Taking O as centre and OP as radius draw a circle.
4. The circle obtained is required.
Answer:
Given: Two circles intersect at two points.
To prove: their centres lie on the perpendicular bisector of the common chord.
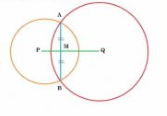
Construction: Joinpoint P and Q to midpoint M of chord AB.
Proof: AB is a chord of circle C(Q,r) and QM is the bisector of chord AB.
Hence,
Similarly, AB is a chord of circle(Q,r' ) and QM is the bisector of chord AB.
Hence,
Now,
PMA and
QMA are forming linear pairs so PMQ is a straight line.
Hence, P and Q lie on the perpendicular bisector of common chord AB.
NCERT Solutions for Class 9 Maths Chapter 10 Circles - Exercise: 10.4
Given: Two circles of radii and
intersect at two points and the distance between their centres is
.
To find the length of the common chord.
Construction: Join OP and draw
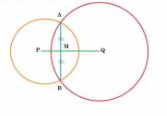
Proof: AB is a chord of circle C(P,3) and PM is the bisector of chord AB.
Let, PM = x , so QM=4-x
In APM, using Pythagoras theorem
...........................1
Also,
In AQM, using Pythagoras theorem
...........................2
From 1 and 2, we get
Put,x=0 in equation 1
Given: two equal chords of a circle intersect within the circle
To prove: Segments of one chord are equal to corresponding segments of the other chord i.e. AP = CP and BP=DP.
Construction : Join OP and draw
Proof :
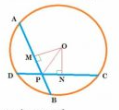
In OMP and
ONP,
AP = AP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
OMP =
ONP (Both are right angled)
Thus, OMP
ONP (By SAS rule)
PM = PN..........................1 (CPCT)
AB = CD ............................2(Given )
......................3
Adding 1 and 3, we have
AM + PM = CN + PN
Subtract 4 from 2, we get
AB-AP = CD - CP
Given: two equal chords of a circle intersect within the circle.
To prove: the line joining the point of intersection to the centre makes equal angles with the chords.
i.e. OPM=
OPN
Proof :
Construction: Join OP and draw
In OMP and
ONP,
AP = AP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
OMP =
ONP (Both are right-angled)
Thus, OMP
ONP (By RHS rule)
OPM=
OPN (CPCT)
Answer:
Given: a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D.
To prove : AB = CD
Construction: Draw
Proof :
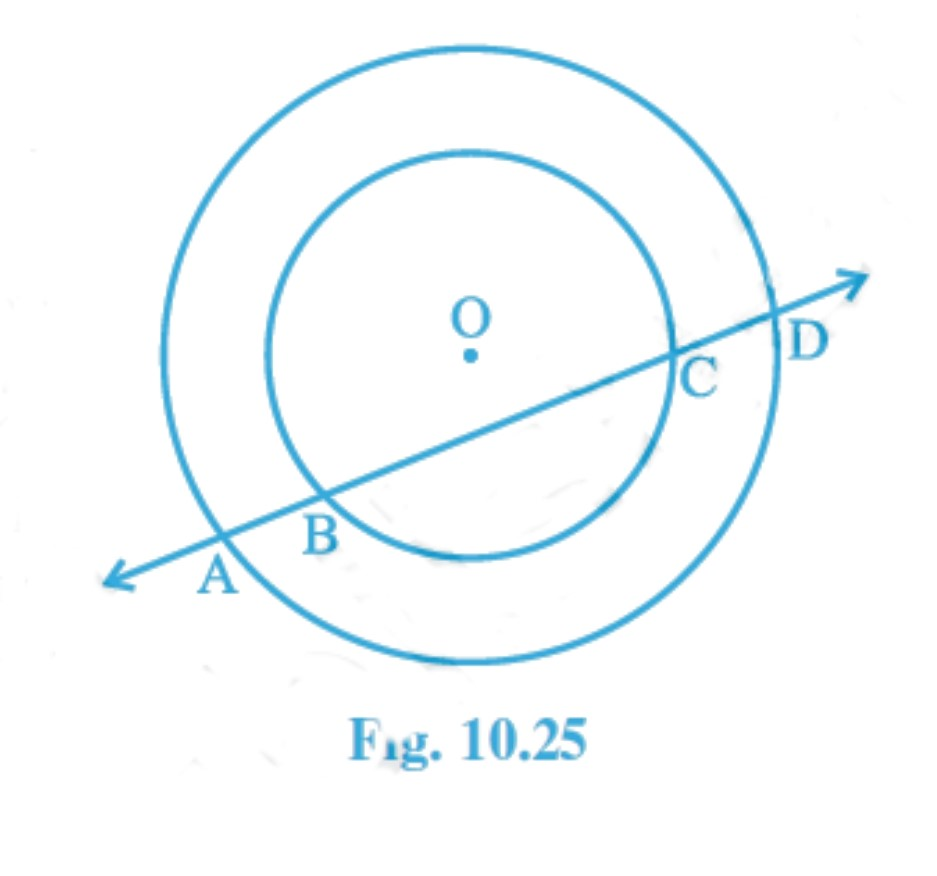
BC is a chord of the inner circle and
So, BM = CM .................1
(Perpendicular OM bisect BC)
Similarly,
AD is a chord of the outer circle and
So, AM = DM .................2
(Perpendicular OM bisect AD )
Subtracting 1 from 2, we get
AM-BM = DM - CM
Answer:
Given: From the figure, R, S, M are the position of Reshma, Salma, Mandip respectively.
So, RS = SM = 6 cm
Construction : Join OR,OS,RS,RM and OM.Draw .
Proof:
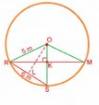 In
In ORS,
OS = OR and (by construction )
So, RL = LS = 3cm (RS = 6 cm )
In OLS, by pytagoras theorem,
In ORK and
OMK,
OR = OM (Radii)
ROK =
MOK (Equal chords subtend equal angle at centre)
OK = OK (Common)
ORK
OMK (By SAS)
RK = MK (CPCT)
Thus,
area of ORS =
...............................1
area of ORS =
.............................2
From 1 and 2, we get
Thus,
Answer:
Given: In the figure, A, S, D are positioned Ankur, Syed and David respectively.
So, AS = SD = AD
Radius of circular park = 20 m
so, AO=SO=DO=20 m
Construction: AP SD
Proof :
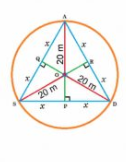
Let AS = SD = AD = 2x cm
In ASD,
AS = AD and AP SD
So, SP = PD = x cm
In OPD, by Pythagoras,
In APD, by Pythagoras,
Squaring both sides,
Hence, length of string of each phone m
NCERT Solutions for Class 9 Maths Chapter 10 Circles - Exercise: 10.5
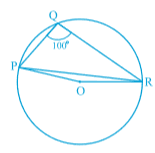
Answer:
AOC =
AOB +
BOC=
AOC = 2
ADC (angle subtended by an arc at the centre is double the angle subtended by it at any)
Answer:
Given: A chord of a circle is equal to the radius of the circle i.e. OA=OB.
To find: ADB and ACB.
Solution :
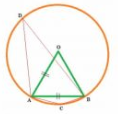 In
In OAB,
OA = AB (Given )
OA = OB (Radii of circle)
So, OA=OB=AB
ABC is a equilateral triangle.
So, AOB =
AOB = 2
ADB
ACBD is a cyclic quadrilateral .
So, ACB+
ADB =
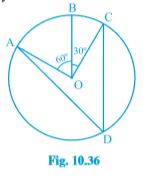
Q3 In Fig. ,
, where P, Q and R are points on a circle with centre O. Find
.
Answer:
Construction: Join PS and RS.
PQRS is a cyclic quadrilateral.
So, PSR +
PQR =
Here, POR = 2
PSR
In OPR ,
OP=OR (Radii )
ORP =
OPR (the angles opposite to equal sides)
In OPR ,
OPR+
ORP+
POR=
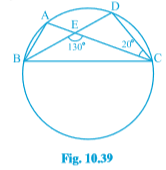 .
.
Answer:
DEC+
BEC =
(linear pairs)
DEC+
=
(
BEC =
)
DEC =
-
DEC =
In DEC,
D+
DEC+
DCE =
D =
BAC (angles in same segment are equal )
BAC =
Answer:
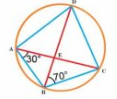
(angles in the same segment are equal )
In
If AB = BC ,then
Here,
Answer:
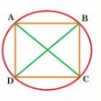
AC is the diameter of the circle.
Thus, and
............................1(Angle in a semi-circle is a right angle)
Similarly, BD is the diameter of the circle.
Thus, and
............................2(Angle in a semi-circle is a right angle)
From 1 and 2, we get
Hence, ABCD is a rectangle.
Q8 If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
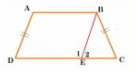
Given: ABCD is a trapezium.
Construction: Draw AD || BE.
Proof: In quadrilateral ABED,
AB || DE (Given )
AD || BE ( By construction )
Thus, ABED is a parallelogram.
AD = BE (Opposite sides of parallelogram )
AD = BC (Given )
so, BE = BC
In EBC,
BE = BC (Proved above )
Thus, ...........1(angles opposite to equal sides )
...............2(Opposite angles of the parallelogram )
From 1 and 2, we get
(linear pair)
Thus, ABED is a cyclic quadrilateral.
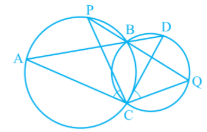
Answer:
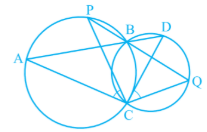
................1(vertically opposite angles)
..................2(Angles in the same segment are equal)
.................3(angles in the same segment are equal)
From 1,2,3 ,we get
Answer:
Given: circles are drawn taking two sides of a triangle as diameters.
Construction: Join AD.
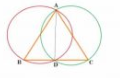
Proof: AB is the diameter of the circle and ADB is formed in a semi-circle.
ADB =
........................1(angle in a semi-circle)
Similarly,
AC is the diameter of the circle and ADC is formed in a semi-circle.
ADC =
........................2(angle in a semi-circle)
From 1 and 2, we have
ADB+
ADC=
+
=
ADB and
ADC are forming a linear pair. So, BDC is a straight line.
Hence, point D lies on this side.
Q11 ABC and ADC are two right triangles with common hypotenuse AC. Prove that
.
Answer:
Given: ABC and ADC are two right triangles with common hypotenuse AC.
To prove :
Proof :
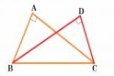
Triangle ABC and ADC are on common base BC and BAC =
BDC.
Thus, point A,B,C,D lie in the same circle.
(If a line segment joining two points subtends equal angles at two other points lying on the same side of line containing line segment, four points lie on the circle.)
CAD =
CBD (Angles in same segment are equal)
Q12 Prove that a cyclic parallelogram is a rectangle.
Answer:
Given: ABCD is a cyclic quadrilateral.
To prove: ABCD is a rectangle.
Proof :
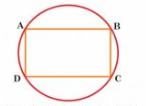
In cyclic quadrilateral ABCD.
.......................1(sum of either pair of opposite angles of a cyclic quadrilateral)
........................................2(opposite angles of a parallelogram are equal )
From 1 and 2,
We know that a parallelogram with one angle right angle is a rectangle.
Hence, ABCD is a rectangle.
NCERT maths chapter 10 class 9 - Exercise: 10.6
Answer:
Given: Circle C(P,r) and circle C(Q,r') intersect each other at A and B.
To prove : PAQ =
PBQ
Proof : In APQ and
BPQ,
PA = PB (radii of same circle)
PQ = PQ (Common)
QA = QB (radii of same circle)
So, APQ
BPQ (By SSS)
PAQ =
PBQ (CPCT)
Answer:
Given : AB = 5 cm, CD = 11 cm and AB || CD.
To find Radius (OA).
Construction: Draw
Proof :
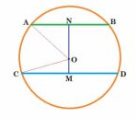
Proof: CD is a chord of circle and
Thus, CM = MD = 5.5 cm (perpendicular from centre bisects chord)
and AN = NB = 2.5 cm
Let OM be x.
So, ON = 6 - x (MN = 6 cm )
In OCM , using Pythagoras,
.............................1
and
In OAN , using Pythagoras,
.............................2
From 1 and 2,
(OC=OA =radii)
From 2, we get
OA = OC
Thus, the radius of the circle is
Answer:
Given : AB = 8 cm, CD = 6 cm , OM = 4 cm and AB || CD.
To find: Length of ON
Construction: Draw
Proof :
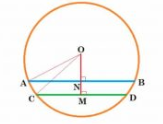
Proof: CD is a chord of circle and
Thus, CM = MD = 3 cm (perpendicular from centre bisects chord)
and AN = NB = 4 cm
Let MN be x.
So, ON = 4 - x (MN = 4 cm )
In OCM , using Pythagoras,
.............................1
and
In OAN , using Pythagoras,
.............................2
From 1 and 2,
(OC=OA =radii)
So, x=1 (since )
ON =4-x =4-1=3 cm
Hence, second chord is 3 cm away from centre.
Answer:
Given : AD = CE
To prove :
Construction: Join AC and DE.
Proof :
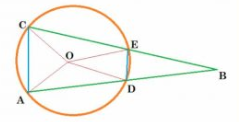
Let ADC = x ,
DOE = y and
AOD = z
So, EOC = z (each chord subtends equal angle at centre)
AOC +
DOE +
AOD +
EOC =
.........................................1
In OAD ,
OA = OD (Radii of the circle)
OAD =
ODA (angles opposite to equal sides )
OAD +
ODA +
AOD =
.............................................................2
Similarly,
.............................................................3
..............................................................4
ODB is exterior of triangle OAD . So,
ODB =
OAD +
ODA
(from 2)
.................................................................5
similarly,
OBE is exterior of triangle OCE . So,
OBE =
OCE +
OEC
(from 3)
.................................................................6
From 4,5,6 ;we get
BDE =
BED =
OEB -
OED
..................................................7
In BDE ,
DBE +
BDE +
BED =
...................................................8
Here, from equation 1,
...................................9
From 8 and 9,we have
Answer:
Given : ABCD is a rhombus.
To prove: the circle drawn with AB as diameter passes through the point O.
Proof :
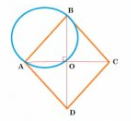
ABCD is rhombus.
Thus, (diagonals of a rhombus bisect each other at
)
So, a circle drawn AB as diameter will pass through point O.
Thus, the circle is drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Answer:
Given: ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E.
To prove : AE = AD
Proof :
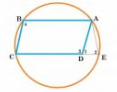
ADC =
3 ,
ABC =
4,
ADE =
1 and
AED =
2
.................1(linear pair)
....................2(sum of opposite angles of cyclic quadrilateral)
3 =
4 (oppsoite angles of parallelogram )
From 1 and 2,
3+
1 =
2 +
4
From 3, 1 =
2
From 4, AQB,
1 =
2
Therefore, AE = AD (In an isosceles triangle ,angles oppsoite to equal sides are equal)
Q7 (i) AC and BD are chords of a circle which bisect each other. Prove that AC and BD are diameters
Answer:
Given: AC and BD are chords of a circle which bisect each other.
To prove: AC and BD are diameters.
Construction : Join AB,BC,CD,DA.
Proof :
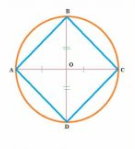
In ABD and
CDO,
AO = OC (Given )
AOB =
COD (Vertically opposite angles )
BO = DO (Given )
So, ABD
CDO (By SAS)
BAO =
DCO (CPCT)
BAO and
DCO are alternate angle and are equal .
So, AB || DC ..............1
Also AD || BC ...............2
From 1 and 2,
......................3(sum of opposite angles)
A =
C ................................4(Opposite angles of the parallelogram )
From 3 and 4,
BD is a diameter of the circle.
Similarly, AC is a diameter.
Q7 (ii) AC and BD are chords of a circle which bisect each other. Prove that ABCD is a rectangle.
Answer:
Given: AC and BD are chords of a circle which bisect each other.
To prove: ABCD is a rectangle.
Construction : Join AB,BC,CD,DA.
Proof :
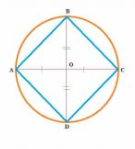
ABCD is a parallelogram. (proved in (i))
(proved in (i))
A parallelogram with one angle , is a rectangle )
Thus, ABCD is rectangle.
Answer:
Given : Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively.
To prove : the angles of the triangle DEF are ,
and
Proof :
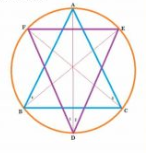
1 and
3 are angles in same segment.therefore,
1 =
3 ................1(angles in same segment are equal )
and 2 =
4 ..................2
Adding 1 and 2,we have
1+
2=
3+
4
,
and
Similarly, and
Answer:
Given: Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles.
To prove : BP = BQ
Proof :
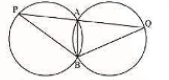
AB is a common chord in both congruent circles.
In
(Sides opposite to equal of the triangle are equal )
Answer:
Given :In any triangle ABC, if the angle bisector of and perpendicular bisector of BC intersect.
To prove : D lies on perpendicular bisector BC.
Construction: Join BD and DC.
Proof :
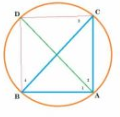
Let ABD =
1 ,
ADC =
2 ,
DCB =
3 ,
CBD =
4
1 and
3 lies in same segment.So,
1 =
3 ..........................1(angles in same segment)
similarly, 2 =
4 ......................2
also, 1=
2 ..............3(given)
From 1,2,3 , we get
3 =
4
Hence, BD = DC (angles opposite to equal sides are equal )
All points lying on perpendicular bisector BC will be equidistant from B and C.
Thus, point D also lies on perpendicular bisector BC.
Interested students can practice these class 9 maths ch 10 question answer using the exercise solutions provided below.
| Chapter No. | Chapter Name |
| Chapter 1 | Number Systems |
| Chapter 2 | Polynomials |
| Chapter 3 | Coordinate Geometry |
| Chapter 4 | Linear Equations In Two Variables |
| Chapter 5 | Introduction to Euclid's Geometry |
| Chapter 6 | Lines And Angles |
| Chapter 7 | Triangles |
| Chapter 8 | Quadrilaterals |
| Chapter 9 | Areas of Parallelograms and Triangles |
| Chapter 10 | Circles |
| Chapter 11 | Constructions |
| Chapter 12 | Heron’s Formula |
| Chapter 13 | Surface Area and Volumes |
| Chapter 14 | Statistics |
| Chapter 15 | Probability |
How To Use NCERT Solutions For Class 9 Maths Chapter 10 Circles
Keep working hard & happy learning!
Circles and the related terms, angle subtended by a chord at a point, perpendicular from the centre to a chord, circle through three points, equal chords and their distances from the centre, angle subtended by an arc of a circle are the important topics of this chapter.
Students in Class 9 can benefit from class 9 chapter 10 maths by gaining a thorough understanding of all the concepts within the subject, which can serve as the basis for their future academic pursuits. The solutions provided by Careers360 experts are designed in a clear and comprehensive manner, making it easier for students to solve complex problems with greater efficiency. By mastering these solutions, CBSE Class 9 students can establish a strong foundation in the fundamentals and achieve excellent scores in their final exams.
The use of class 9th circles NCERT solutions is a reliable and effective approach to help students develop mastery of the subject's concepts. Reviewing these solutions, in conjunction with the textbooks, can aid in solving any problems that may arise on the board exams. These solutions also enhance students' problem-solving skills and logical reasoning abilities. They are among the most widely used study materials for CBSE exams. Consistent practice with these solutions can improve students' performance and help them excel in the subject.
Here you will get the detailed NCERT solutions for class 9. you can practice these maths ch 10 class 9 solutions and problems to command the concepts discussed in the chapter. after practicing you will get confidence to solve any kind of problem related to circle given in class 9th.
Late Fee Application Date:22 July,2024 - 31 July,2024
Late Fee Application Date:22 July,2024 - 31 July,2024

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Get up to 90% scholarship on NEET, JEE & Foundation courses

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Accepted by more than 11,000 universities in over 150 countries worldwide

Register now for PTE & Save 5% on English Proficiency Tests with ApplyShop Gift Cards