NCERT Solutions for Exercise 10.6 Class 9 Maths Chapter 10 - Circles

Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with

Plan, Prepare & Make the Best Career Choices

NCERT Solutions for Exercise 10.6 Class 9 Maths Chapter 10 - Circles

Edited By safeer | Updated on Jul 29, 2022 06:39 PM IST

The NCERT Solutions for Class 9 Maths exercise 10.6 is a discretionary (not according to the assessment perspective for Class 9) exercise that contains points like equal chords of a circle, cyclic quadrilaterals, angle extended by an arc of a circle and finding lengths of the radius when the distance of chord and chord length is given.

Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

New: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

Circles Class 9 Chapter 10 Exercise: 10.6
More About NCERT Solutions for Class 9 Maths Exercise 10.6
Benefits of NCERT Solutions for Class 9 Maths Exercise 10.6
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions

A few important concepts related to NCERT syllabus Class 9 Maths chapter 10 exercise 10.6 in order to solve this exercise are:

The sum of any two opposite angles of a cyclic quadrilateral is 180°
Angles which are present in the same arc of the circle are equal.
The point subtended by an arc (circular segment) at the circle's centre is twofold the angle subtended by it at the remaining circumference of the circle.
The chords of equivalent length are consistently equidistant from the centre of the circle

Significant questions in this exercise utilize a mix of at least two of the above ideas.

Along with NCERT book Class 9 Maths chapter 10 exericse 10.6 the following exercises are also present.

Circles Class 9 Chapter 10 Exercise: 10.6

Q1 Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

Answer:

Given: Circle C(P,r) and circle C(Q,r') intersect each other at A and B.

To prove : $\angle$ PAQ = $\angle$ PBQ

Proof : In $\triangle$ APQ and $\triangle$ BPQ,

PA = PB (radii of same circle)

PQ = PQ (Common)

QA = QB (radii of same circle)

So, $\triangle$ APQ $\cong$ $\triangle$ BPQ (By SSS)

$\angle$ PAQ = $\angle$ PBQ (CPCT)

Q2 Two chords AB and CD of lengths $\small 5\hspace {1mm}cm$ and $\small 11\hspace {1mm}cm$ respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is $\small 6\hspace {1mm}cm$ , find the radius of the circle.

Answer:

Given : AB = 5 cm, CD = 11 cm and AB || CD.

To find Radius (OA).

Construction: Draw $OM \perp CD \, \, and \, \, \, ON\perp AB$

Proof :

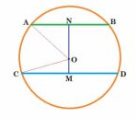
1640237834315

Proof: CD is a chord of circle and $OM \perp CD$

Thus, CM = MD = 5.5 cm (perpendicular from centre bisects chord)

and AN = NB = 2.5 cm

Let OM be x.

So, ON = 6 - x (MN = 6 cm )

In $\triangle$ OCM , using Pythagoras,

$OC ^2=CM^2+OM^2$ .............................1

and

In $\triangle$ OAN , using Pythagoras,

$OA ^2=AN^2+ON^2$ .............................2

From 1 and 2,

$CM ^2+OM^2=AN^2+ON^2$ (OC=OA =radii)

$5.5 ^2+x^2=2.5^2+(6-x)^2$

$\Rightarrow 30.25+x^2=6.25+36+x^2-12x$

$\Rightarrow 30.25-42.25=-12x$

$\Rightarrow -12=-12x$

$\Rightarrow x=1$

From 2, we get

$OC^2=5.5^2+1^2=30.25+1=31.25$

$\Rightarrow OC=\frac{5}{2}\sqrt{5} cm$

OA = OC

Thus, the radius of the circle is $\frac{5}{2}\sqrt{5} cm$

Q3 The lengths of two parallel chords of a circle are $\small 6\hspace {1mm}cm$ and $\small 8\hspace {1mm}cm$ . If the smaller chord is at distance $\small 4\hspace {1mm}cm$ from the centre, what is the distance of the other chord from the centre?

Answer:

Given : AB = 8 cm, CD = 6 cm , OM = 4 cm and AB || CD.

To find: Length of ON

Construction: Draw $OM \perp CD \, \, and \, \, \, ON\perp AB$

Proof :

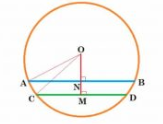
1640237861219

Proof: CD is a chord of circle and $OM \perp CD$

Thus, CM = MD = 3 cm (perpendicular from centre bisects chord)

and AN = NB = 4 cm

Let MN be x.

So, ON = 4 - x (MN = 4 cm )

In $\triangle$ OCM , using Pythagoras,

$OC ^2=CM^2+OM^2$ .............................1

and

In $\triangle$ OAN , using Pythagoras,

$OA ^2=AN^2+ON^2$ .............................2

From 1 and 2,

$CM ^2+OM^2=AN^2+ON^2$ (OC=OA =radii)

$\Rightarrow 3 ^2+4^2=4^2+(4-x)^2$

$\Rightarrow 9+16=16+16+x^2-8x$

$\Rightarrow 9=16+x^2-8x$

$\Rightarrow x^2-8x+7=0$

$\Rightarrow x^2-7x-x+7=0$

$\Rightarrow x(x-7)-1(x-7)=0$

$\Rightarrow (x-1)(x-7)=0$

$\Rightarrow x=1,7$

So, x=1 (since $x\neq 7> OM$ )

ON =4-x =4-1=3 cm

Hence, second chord is 3 cm away from centre.

Q4 Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that $\small \angle ABC$ is equal to half the difference of the angles subtended by the chords AC and DE at the centre.

Answer:

Given : AD = CE

To prove : $\angle ABC = \frac{1}{2}(\angle AOC-\angle DOE)$

Construction: Join AC and DE.

Proof :

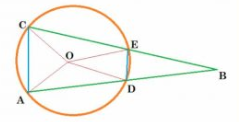
1640237883312

Let $\angle$ ADC = x , $\angle$ DOE = y and $\angle$ AOD = z

So, $\angle$ EOC = z (each chord subtends equal angle at centre)

$\angle$ AOC + $\angle$ DOE + $\angle$ AOD + $\angle$ EOC = $360 \degree$

$\Rightarrow x+y+z+z=360 \degree$

$\Rightarrow x+y+2z=360 \degree$ .........................................1

In $\triangle$ OAD ,

OA = OD (Radii of the circle)

$\angle$ OAD = $\angle$ ODA (angles opposite to equal sides )

$\angle$ OAD + $\angle$ ODA + $\angle$ AOD = $180 \degree$

$\Rightarrow 2\angle OAD+z=180 \degree$

$\Rightarrow 2\angle OAD=180 \degree-z$

$\Rightarrow \angle OAD=\frac{180 \degree-z}{2}$

$\Rightarrow \angle OAD=90 \degree-\frac{z}{2}$ .............................................................2

Similarly,

$\Rightarrow \angle OCE=90 \degree-\frac{x}{2}$ .............................................................3

$\Rightarrow \angle OED=90 \degree-\frac{y}{2}$ ..............................................................4

$\angle$ ODB is exterior of triangle OAD . So,

$\angle$ ODB = $\angle$ OAD + $\angle$ ODA

$\Rightarrow \angle ODB=90 \degree-\frac{z}{2}+z$ (from 2)

$\Rightarrow \angle ODB=90 \degree+\frac{z}{2}$ .................................................................5

similarly,

$\angle$ OBE is exterior of triangle OCE . So,

$\angle$ OBE = $\angle$ OCE + $\angle$ OEC

$\Rightarrow \angle OEB=90 \degree-\frac{z}{2}+z$ (from 3)

$\Rightarrow \angle OEB=90 \degree+\frac{z}{2}$ .................................................................6

From 4,5,6 ;we get

$\angle$ BDE = $\angle$ BED = $\angle$ OEB - $\angle$ OED

$\Rightarrow \angle BDE=\angle BED=90 \degree+\frac{z}{2}-(90-\frac{y}{2})=\frac{y+z}{2}$

$\Rightarrow \angle BDE+\angle BED=y+z$ ..................................................7

In $\triangle$ BDE ,

$\angle$ DBE + $\angle$ BDE + $\angle$ BED = $180 \degree$

$\Rightarrow \angle DBE +y+z=180 \degree$

$\Rightarrow \angle DBE =180 \degree-(y+z)$

$\Rightarrow \angle ABC =180 \degree-(y+z)$ ...................................................8

Here, from equation 1,

$\frac{x-y}{2}=\frac{360 \degree-y-2x-y}{2}$

$\Rightarrow \frac{x-y}{2}=\frac{360 \degree-2y-2x}{2}$

$\Rightarrow \frac{x-y}{2}=180 \degree-y-x$ ...................................9

From 8 and 9,we have

$\angle ABC=\frac{x-y}{2}=\frac{1}{2}(\angle AOC-\angle DOE)$

Q5 Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.

Answer:

Given : ABCD is a rhombus.

To prove: the circle drawn with AB as diameter passes through the point O.

Proof :

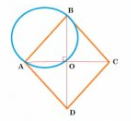
1640237931704

ABCD is rhombus.

Thus, $\angle AOC = 90 \degree$ (diagonals of a rhombus bisect each other at $90 \degree$ )

So, a circle drawn AB as diameter will pass through point O.

Thus, the circle is drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.

Q6 ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that $\small AE=AD$ .

Answer:

Given: ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E.

To prove : AE = AD

Proof :

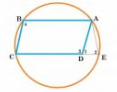
1640237957576

$\angle$ ADC = $\angle$ 3 , $\angle$ ABC = $\angle$ 4, $\angle$ ADE = $\angle$ 1 and $\angle$ AED = $\angle$ 2

$\angle 3+\angle 1=180 \degree$ .................1(linear pair)

$\angle 2+\angle 4=180 \degree$ ....................2(sum of opposite angles of cyclic quadrilateral)

$\angle$ 3 = $\angle$ 4 (oppsoite angles of parallelogram )

From 1 and 2,

$\angle$ 3+ $\angle$ 1 = $\angle$ 2 + $\angle$ 4

From 3, $\angle$ 1 = $\angle$ 2

From 4, $\triangle$ AQB, $\angle$ 1 = $\angle$ 2

Therefore, AE = AD (In an isosceles triangle ,angles oppsoite to equal sides are equal)

Q7 (i) AC and BD are chords of a circle which bisect each other. Prove that AC and BD are diameters

Answer:

Given: AC and BD are chords of a circle which bisect each other.

To prove: AC and BD are diameters.

Construction : Join AB,BC,CD,DA.

Proof :

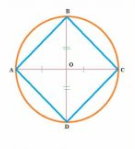
1640237982446

In $\triangle$ ABD and $\triangle$ CDO,

AO = OC (Given )

$\angle$ AOB = $\angle$ COD (Vertically opposite angles )

BO = DO (Given )

So, $\triangle$ ABD $\cong$ $\triangle$ CDO (By SAS)

$\angle$ BAO = $\angle$ DCO (CPCT)

$\angle$ BAO and $\angle$ DCO are alternate angle and are equal .

So, AB || DC ..............1

Also AD || BC ...............2

From 1 and 2,

$\angle A+\angle C=180 \degree$ ......................3(sum of opposite angles)

$\angle$ A = $\angle$ C ................................4(Opposite angles of the parallelogram )

From 3 and 4,

$\angle A+\angle A=180 \degree$

$\Rightarrow 2\angle A=180 \degree$

$\Rightarrow \angle A=90 \degree$

BD is a diameter of the circle.

Similarly, AC is a diameter.

Q7 (ii) AC and BD are chords of a circle which bisect each other. Prove that ABCD is a rectangle.

Answer:

Given: AC and BD are chords of a circle which bisect each other.

To prove: ABCD is a rectangle.

Construction : Join AB,BC,CD,DA.

Proof :

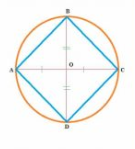
1656935732366

ABCD is a parallelogram. (proved in (i))

$\angle A=90 \degree$ (proved in (i))

A parallelogram with one angle $90 \degree$ , is a rectangle )

Thus, ABCD is rectangle.

Q8 Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are $\small 90^{\circ}-\frac{1}{2}C$ , $\small 90^{\circ}-\frac{1}{2}B$ and $\small 90^{\circ}-\frac{1}{2}A$

Answer:

Given : Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively.

To prove : the angles of the triangle DEF are $\small 90^{\circ}-\frac{1}{2}C$ , $\small 90^{\circ}-\frac{1}{2}B$ and $\small 90^{\circ}-\frac{1}{2}A$

Proof :

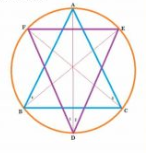
1640238007328

$\angle$ 1 and $\angle$ 3 are angles in same segment.therefore,

$\angle$ 1 = $\angle$ 3 ................1(angles in same segment are equal )

and $\angle$ 2 = $\angle$ 4 ..................2

Adding 1 and 2,we have

$\angle$ 1+ $\angle$ 2= $\angle$ 3+ $\angle$ 4

$\Rightarrow \angle D=\frac{1}{2}\angle B+\frac{1}{2}\angle C$ ,

$\Rightarrow \angle D=\frac{1}{2}(\angle B+\angle C)$

$\Rightarrow \angle D=\frac{1}{2}(180 \degree+\angle C)$

and $\Rightarrow \angle D=\frac{1}{2}(180 \degree-\angle A)$

$\Rightarrow \angle D=90 \degree-\frac{1}{2}\angle A$

Similarly, $\Rightarrow \angle E=90 \degree-\frac{1}{2}\angle B$ and $\angle F=90 \degree-\frac{1}{2}\angle C$

Q9 Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that $\small BP=BQ$ .

Answer:

Given: Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles.

To prove : BP = BQ

Proof :

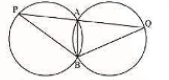
1640238028954

AB is a common chord in both congruent circles.

$\therefore \angle APB = \angle AQB$

In $\triangle BPQ,$

$\angle APB = \angle AQB$

$\therefore BQ = BP$ (Sides opposite to equal of the triangle are equal )

Q10 In any triangle ABC, if the angle bisector of $\small \angle A$ and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.

Answer:

Given :In any triangle ABC, if the angle bisector of $\small \angle A$ and perpendicular bisector of BC intersect.

To prove : D lies on perpendicular bisector BC.

Construction: Join BD and DC.

Proof :

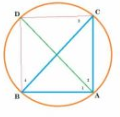
1640238078439

Let $\angle$ ABD = $\angle$ 1 , $\angle$ ADC = $\angle$ 2 , $\angle$ DCB = $\angle$ 3 , $\angle$ CBD = $\angle$ 4

$\angle$ 1 and $\angle$ 3 lies in same segment.So,

$\angle$ 1 = $\angle$ 3 ..........................1(angles in same segment)

similarly, $\angle$ 2 = $\angle$ 4 ......................2

also, $\angle$ 1= $\angle$ 2 ..............3(given)

From 1,2,3 , we get

$\angle$ 3 = $\angle$ 4

Hence, BD = DC (angles opposite to equal sides are equal )

All points lying on perpendicular bisector BC will be equidistant from B and C.

Thus, point D also lies on perpendicular bisector BC.

Benefits of NCERT Solutions for Class 9 Maths Exercise 10.6

Exercise 10.6 Class 9 Maths, is based on circles and the majority of the critical properties of circles.
From Class 9 Maths chapter 10 exercise 10.6 we get to revise and give a final touchup to the whole ideas of this part in a solitary exercise.
Understanding the concepts from Class 9 Maths chapter 10 exercise 10.6 will make the ideas and questions from better and competitive standards (like Class10) simpler for us.

Also, See

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What are the main things you learned from NCERT solutions for Class 9 Maths exercise 10.6?

This exercise deals with all the perspectives that associate the difficult questions regarding circles and their properties.

2. How can you describe a circle?

A circle can be characterized as a closed (shut figure), two-dimensional bent (curved) shape, with zero corners to such an extent that each point of the circumference of the circle is equidistance from the proper centre of the circle.

3. How many circles can be drawn from three non-colinear points?

If three non-colinear points are given then there is one and only one circle that passes through all of the points.

4. What is the measurement of the opposite angle in a cyclic quadrilateral if one of them is 135?

The Sum of any two opposite angles of a cyclic quadrilateral is 180°

The other angle =180-135=45

5. What is a tangent?

Tangent is a straight line that passes through only one point of the circle’s circumference.

6. Can we get any chord that has length greater than the diameter of the circle?

No, we can’t get any chord that is greater or equal to the diameter of the circle as the diameter is the largest chord.

7. In a cyclic quadrilateral the opposite angles are at the ratio of 2:3 then find the angles?

The Sum of any two opposite angles of a cyclic quadrilateral is 180°

Sum of ratio = 5

Angles are:

2/5 times 180 and 3/5 times 180

The angles are 72 and 108

8. How many tangents can be drawn from a given point of the circle’s circumference?

One and only one tangent is possible through one given point of the circumference.

Also Read

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Books for Class 9 English 2024 - Download All Chapters Pdf

NCERT Books for Class 9 Social Science 2024 - Download PDF

NCERT Books for Class 9 2024 - Free PDFs All Subjects Download

NCERT Books for Class 9 Hindi 2024 - Download PDF

NCERT Books for Class 9 Science 2023-24 - Download PDF (All Chapters)

NCERT Books for Class 9 Maths 2023-24 - Download PDF

NCERT Syllabus for Class 9 Social Science 2024 - Download PDF

NCERT Syllabus for Class 9 2024 - Download All subjects Pdf

NCERT Syllabus for Class 9 Hindi 2024 - Download PDF

NCERT Syllabus for Class 9 Science 2024 - Download Chapter Wise Pdf

NCERT Syllabus for class 9 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions for Class 9 - All Subjects PDF Download

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.1 Number Systems

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

DU LLB Merit List 2024 - Rank List, Tie Breaker Rules

Apr 25, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

Apr 16, 2024

Graphic Designing Courses after 12th - Eligibility & Top Institutes

Apr 03, 2024

Navyug School Admission 2024: Apply now | Admissions Open for 2024-25

Mar 26, 2024

NSSNET Result 2024, Check Navyug School Admission Test Here

Mar 22, 2024

NSSNET Admit Card 2024 (Out), Navyug School Entrance NTA Hall ticket

Mar 22, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

Apr 16, 2024

Physiotherapy Courses after 12th - Eligibility & Top Institutes

Mar 16, 2024

Explore Premium

Mental Health

Understand Your Attachment Style And Learn How You Can Reform Your Relationships

7 min ⋆ Apr 09, 2023

Mental Health

7 Tips To Convey Your Struggles To Your Loved Ones

5 min ⋆ Mar 18, 2023

Mental Health

Decision-Making: Common Challenges Faced, Tips To Make Good Decisions

6 min ⋆ Feb 24, 2023

Parenting

How Stay-At-Home Parents Can Care For Themselves

6 min ⋆ Apr 20, 2023

Parenting

Teenage Relationships: Tips To Help Your Teenager Deal With A Breakup

6 min ⋆ Jan 13, 2023

Parenting

Getting Over The Pink and Blue Divide: Revising Gender Roles

4 min ⋆ Mar 05, 2022

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:28 April,2024 - 28 April,2024

Exam Pattern

Result

Mock Test

Jammu and Kashmir State Board of School Education 12th Examination

Exam Date:28 April,2024 - 28 April,2024

Exam Pattern

Result

Mock Test

View All School Exams

Get answers from students and experts

Explore Career Options (By Industry)

Data Administrator

Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.

4 Jobs Available

Bio Medical Engineer

The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary.

4 Jobs Available

Ethical Hacker

A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.

3 Jobs Available

GIS Expert

GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.

3 Jobs Available

Data Analyst

The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

3 Jobs Available

Geothermal Engineer

Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.

3 Jobs Available

Database Architect

If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi.

3 Jobs Available

Remote Sensing Technician

Individuals who opt for a career as a remote sensing technician possess unique personalities. Remote sensing analysts seem to be rational human beings, they are strong, independent, persistent, sincere, realistic and resourceful. Some of them are analytical as well, which means they are intelligent, introspective and inquisitive.

Remote sensing scientists use remote sensing technology to support scientists in fields such as community planning, flight planning or the management of natural resources. Analysing data collected from aircraft, satellites or ground-based platforms using statistical analysis software, image analysis software or Geographic Information Systems (GIS) is a significant part of their work. Do you want to learn how to become remote sensing technician? There's no need to be concerned; we've devised a simple remote sensing technician career path for you. Scroll through the pages and read.

3 Jobs Available

Budget Analyst

Budget analysis, in a nutshell, entails thoroughly analyzing the details of a financial budget. The budget analysis aims to better understand and manage revenue. Budget analysts assist in the achievement of financial targets, the preservation of profitability, and the pursuit of long-term growth for a business. Budget analysts generally have a bachelor's degree in accounting, finance, economics, or a closely related field. Knowledge of Financial Management is of prime importance in this career.

4 Jobs Available

Data Analyst

3 Jobs Available

Underwriter

An underwriter is a person who assesses and evaluates the risk of insurance in his or her field like mortgage, loan, health policy, investment, and so on and so forth. The underwriter career path does involve risks as analysing the risks means finding out if there is a way for the insurance underwriter jobs to recover the money from its clients. If the risk turns out to be too much for the company then in the future it is an underwriter who will be held accountable for it. Therefore, one must carry out his or her job with a lot of attention and diligence.

3 Jobs Available

Finance Executive

3 Jobs Available

Product Manager

A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.

3 Jobs Available

Operations Manager

Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.

3 Jobs Available

Stock Analyst

Individuals who opt for a career as a stock analyst examine the company's investments makes decisions and keep track of financial securities. The nature of such investments will differ from one business to the next. Individuals in the stock analyst career use data mining to forecast a company's profits and revenues, advise clients on whether to buy or sell, participate in seminars, and discussing financial matters with executives and evaluate annual reports.

2 Jobs Available

Researcher

A Researcher is a professional who is responsible for collecting data and information by reviewing the literature and conducting experiments and surveys. He or she uses various methodological processes to provide accurate data and information that is utilised by academicians and other industry professionals. Here, we will discuss what is a researcher, the researcher's salary, types of researchers.

2 Jobs Available

Welding Engineer

Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.

5 Jobs Available

Transportation Planner

A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.

3 Jobs Available

Environmental Engineer

Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems.

2 Jobs Available

Safety Manager

A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.

2 Jobs Available

Conservation Architect

A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.

2 Jobs Available

Structural Engineer

A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.

2 Jobs Available

Highway Engineer

Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.

2 Jobs Available

Field Surveyor

Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials.

2 Jobs Available

Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available

Pathologist

A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.

5 Jobs Available

Veterinary Doctor

5 Jobs Available

Speech Therapist

4 Jobs Available

Gynaecologist

Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth.

4 Jobs Available

Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available

Oncologist

An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.

3 Jobs Available

Anatomist

Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.

2 Jobs Available

Actor

For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs.

4 Jobs Available

Acrobat

Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.

3 Jobs Available

Video Game Designer

Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages.

Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.

3 Jobs Available

Radio Jockey

Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.

A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.

3 Jobs Available

Choreographer

The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.

2 Jobs Available

Social Media Manager

A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.

2 Jobs Available

Photographer

Photography is considered both a science and an art, an artistic means of expression in which the camera replaces the pen. In a career as a photographer, an individual is hired to capture the moments of public and private events, such as press conferences or weddings, or may also work inside a studio, where people go to get their picture clicked. Photography is divided into many streams each generating numerous career opportunities in photography. With the boom in advertising, media, and the fashion industry, photography has emerged as a lucrative and thrilling career option for many Indian youths.

2 Jobs Available

Producer

An individual who is pursuing a career as a producer is responsible for managing the business aspects of production. They are involved in each aspect of production from its inception to deception. Famous movie producers review the script, recommend changes and visualise the story.

They are responsible for overseeing the finance involved in the project and distributing the film for broadcasting on various platforms. A career as a producer is quite fulfilling as well as exhaustive in terms of playing different roles in order for a production to be successful. Famous movie producers are responsible for hiring creative and technical personnel on contract basis.

2 Jobs Available

Copy Writer

In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook.

5 Jobs Available

Vlogger

In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion.

Ever since internet costs got reduced the viewership for these types of content has increased on a large scale. Therefore, a career as a vlogger has a lot to offer. If you want to know more about the Vlogger eligibility, roles and responsibilities then continue reading the article.

3 Jobs Available

Publisher

For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.

3 Jobs Available

Journalist

Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.

3 Jobs Available

Editor

Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.

3 Jobs Available

Reporter

Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.

2 Jobs Available

Corporate Executive

Are you searching for a Corporate Executive job description? A Corporate Executive role comes with administrative duties. He or she provides support to the leadership of the organisation. A Corporate Executive fulfils the business purpose and ensures its financial stability. In this article, we are going to discuss how to become corporate executive.

2 Jobs Available

Multimedia Specialist

A multimedia specialist is a media professional who creates, audio, videos, graphic image files, computer animations for multimedia applications. He or she is responsible for planning, producing, and maintaining websites and applications.

2 Jobs Available

Welding Engineer

5 Jobs Available

QA Manager

4 Jobs Available

Quality Controller

A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product.

A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.

3 Jobs Available

Production Manager

3 Jobs Available

Product Manager

3 Jobs Available

QA Lead

A QA Lead is in charge of the QA Team. The role of QA Lead comes with the responsibility of assessing services and products in order to determine that he or she meets the quality standards. He or she develops, implements and manages test plans.

2 Jobs Available

Structural Engineer

2 Jobs Available

Process Development Engineer

The Process Development Engineers design, implement, manufacture, mine, and other production systems using technical knowledge and expertise in the industry. They use computer modeling software to test technologies and machinery. An individual who is opting career as Process Development Engineer is responsible for developing cost-effective and efficient processes. They also monitor the production process and ensure it functions smoothly and efficiently.

2 Jobs Available

QA Manager

4 Jobs Available

AWS Solution Architect

An AWS Solution Architect is someone who specializes in developing and implementing cloud computing systems. He or she has a good understanding of the various aspects of cloud computing and can confidently deploy and manage their systems. He or she troubleshoots the issues and evaluates the risk from the third party.

4 Jobs Available

Azure Administrator

An Azure Administrator is a professional responsible for implementing, monitoring, and maintaining Azure Solutions. He or she manages cloud infrastructure service instances and various cloud servers as well as sets up public and private cloud systems.

4 Jobs Available

Computer Programmer

Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.

3 Jobs Available

Product Manager

3 Jobs Available

Information Security Manager

Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack

3 Jobs Available

ITSM Manager

3 Jobs Available

Automation Test Engineer

An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process.

2 Jobs Available

Everything about Education

Latest updates, Exclusive Content, Webinars and more.

Subscribe to Premium

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

250M+
Students
30,000+
Colleges
500+
Exams
1500+
E-Books
12000+
Cetifications

We Appeared in

Explore Top Colleges Accepting Applications

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Animation Courses

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Exercise 10.6 Class 9 Maths Chapter 10 - Circles

Circles Class 9 Chapter 10 Exercise: 10.6

More About NCERT Solutions for Class 9 Maths Exercise 10.6

Benefits of NCERT Solutions for Class 9 Maths Exercise 10.6

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

Also Read

Articles

Explore Premium

Understand Your Attachment Style And Learn How You Can Reform Your Relationships

7 Tips To Convey Your Struggles To Your Loved Ones

Decision-Making: Common Challenges Faced, Tips To Make Good Decisions

How Stay-At-Home Parents Can Care For Themselves

Teenage Relationships: Tips To Help Your Teenager Deal With A Breakup

Getting Over The Pink and Blue Divide: Revising Gender Roles

Upcoming School Exams

National Institute of Open Schooling 12th Examination