NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3 - Circles
The smooth curve joining two points on a circle is called an arc. It is part of the circumference of the circle. In a circle chord is a line segment that joins the two endpoints on the circumference. This chord divides the circle into two different parts: one is a major part, and it is called the major arc, and the other is a minor part, and it is called the minor arc. If two chords are equal in a circle, then their corresponding arcs are congruent.
This Story also Contains
- NCERT Solutions for Class 9 Maths Chapter 9 – Circles Exercise 9.3
- Access Circles Class 9 Chapter 9 Exercise: 9.3
- Topics Covered in Chapter 9 Circles: Exercise 9.3
- NCERT Solutions of Class 9 Subject Wise
- NCERT Subject-Wise Exemplar Solutions

Chapter 9 in class 9 is about circles and the basic definition of circles, chords, segments, arcs and related questions with solutions already discussed in exercises 9.1 and 9.2. In exercise 9.3, students get the solutions to the questions given in the NCERT exercise. These questions are based on the chords, arcs, and perpendicular lines. These solutions will help you to understand the concept. All the solutions are detailed and explained in understandable language. This will help you to ace the topic through regular practice of the questions. Students can also find solutions to the NCERT Books in PDF format, so the solutions can be used offline. Students can also download NCERT Solutions according to their standard and requirements.
**Please be aware that this chapter has been renumbered as Chapter 9 in the CBSE Syllabus for the academic year 2023-24.
Access Circles Class 9 Chapter 9 Exercise: 9.3
![]()
Solution:
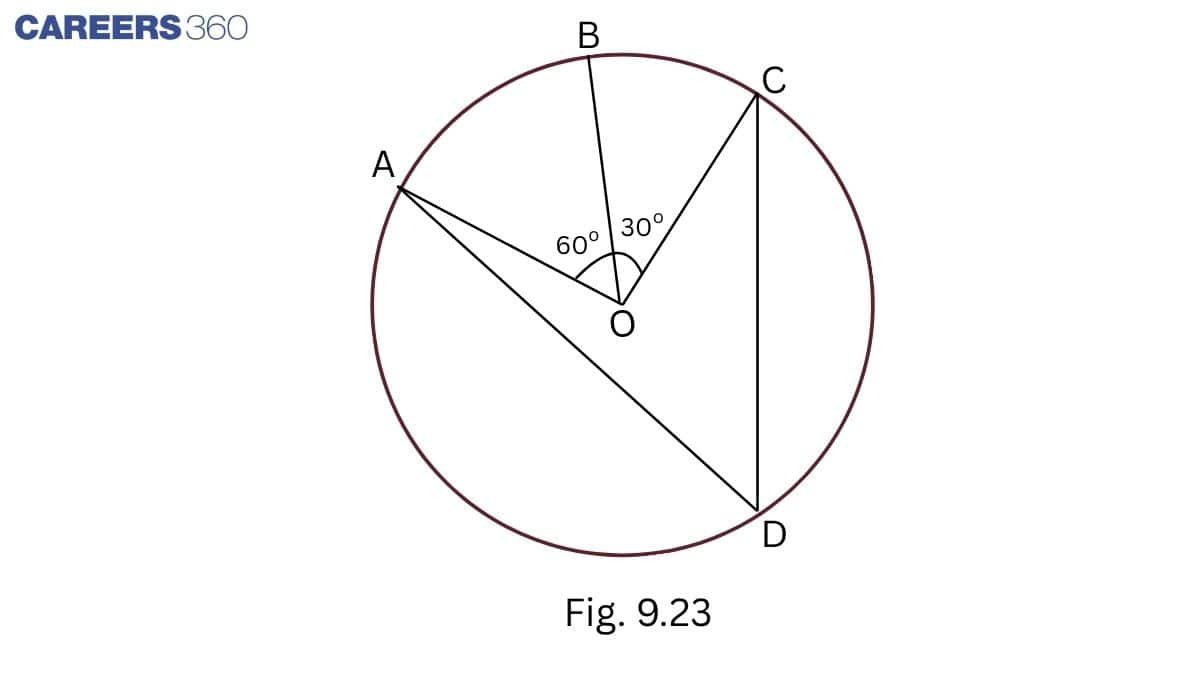
∠ AOC = ∠ AOB + ∠ BOC = 60∘+30∘=90∘
∠ AOC = 2 ∠ ADC (angle subtended by an arc at the centre is double the angle subtended by it at any)
∠ADC=12∠AOC
⇒∠ADC=1290∘=45∘
Solution:
Given: A chord of a circle is equal to the radius of the circle i.e. OA = AB.
To find: ∠ADB and ∠ ACB.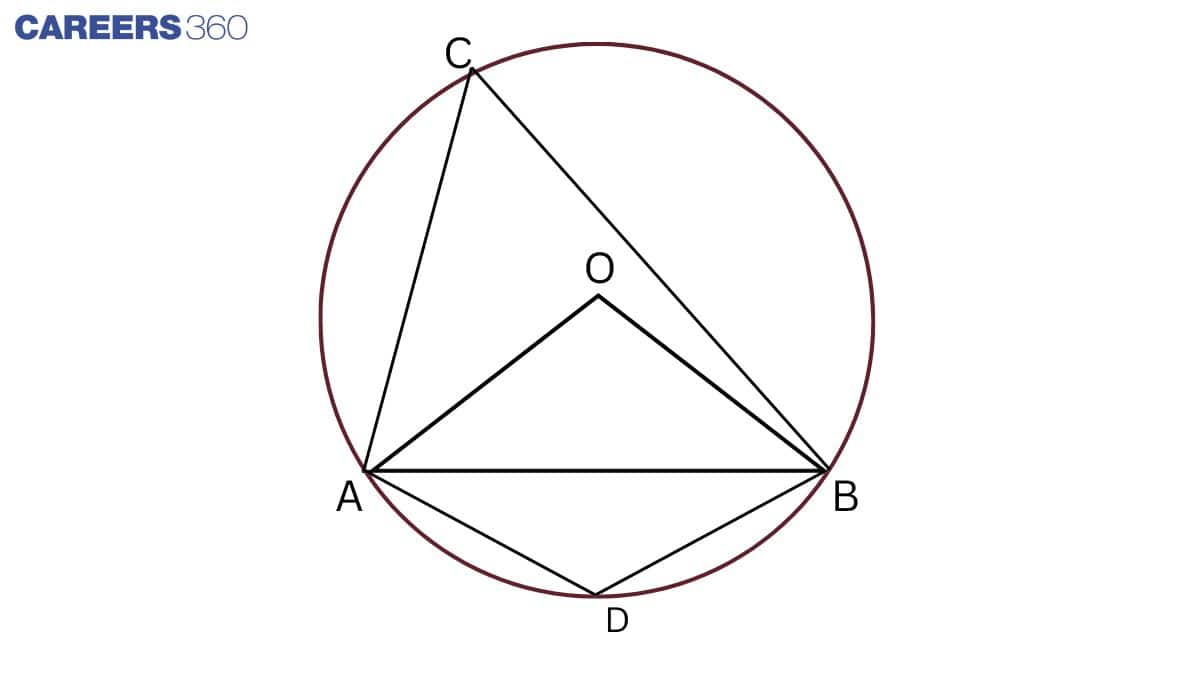
In △ OAB,OA = AB (Given)
OA = OB (Radii of circle)
So, OA = OB = AB
⇒ AOB is an equilateral triangle.
So, ∠ AOB = 60∘
∠ AOB = 2 ∠ ADB
⇒∠ADB=12∠AOB
⇒∠ADB=1260∘=30
ACBD is a cyclic quadrilateral.
So, ∠ ACB+ ∠ ADB = 180∘
⇒∠ACB+30∘=180∘
⇒∠ACB=180∘−30∘=150∘
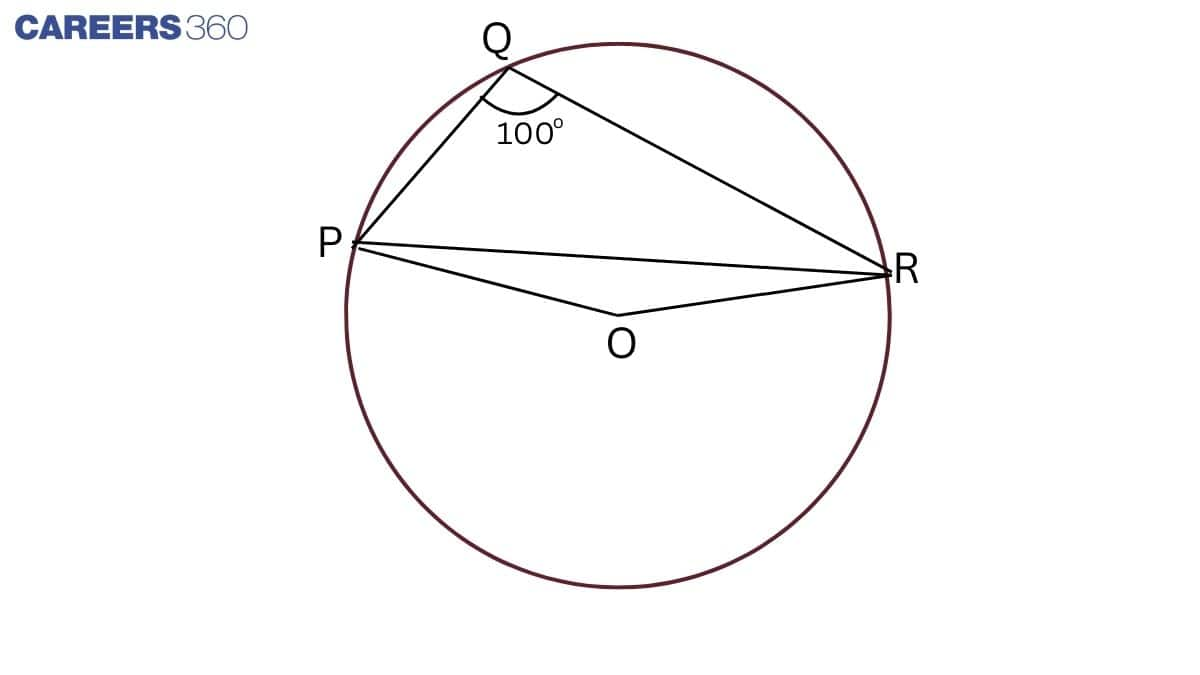
Q3 In Fig. 10.37 , ∠PQR=100∘ , where P, Q and R are points on a circle with centre O. Find ∠OPR .
Solution:

Construction: Join PO and OR.
PQSR is a cyclic quadrilateral.
So, ∠ PSR + ∠ PQR = 180∘
⇒∠PSR+100∘=180∘
⇒∠PSR=180∘−100∘=80∘
Here, ∠ POR = 2 ∠ PSR
⇒∠POR=2×80∘=160∘
In △ OPR,
OP = OR (Radii)
∠ ORP = ∠ OPR (the angles opposite to equal sides)
In △ OPR,
∠ OPR+ ∠ ORP + ∠ POR = 180∘
⇒2∠OPR+160∘=180∘
⇒2∠OPR=180∘−160∘
⇒2∠OPR=20∘
⇒∠OPR=10∘
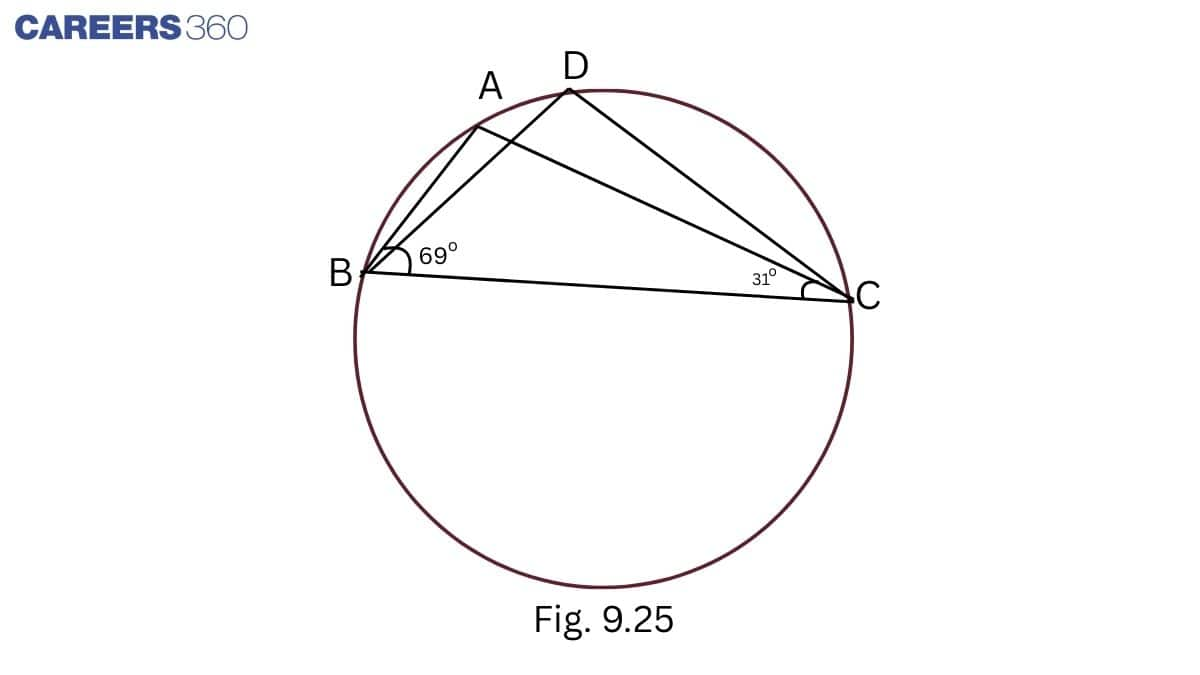
Q4 In Fig. 10.38 , ∠ABC=69∘,∠ACB=31∘, find ∠BDC
Solution:
In △ ABC,
∠ A+ ∠ ABC+ ∠ ACB= 180∘
⇒∠A+69∘+31∘=180∘
⇒∠A+100∘=180∘
⇒∠A=180∘−100∘
⇒∠A=80∘
∠ A = ∠ BDC = 80∘ (Angles in same segment)
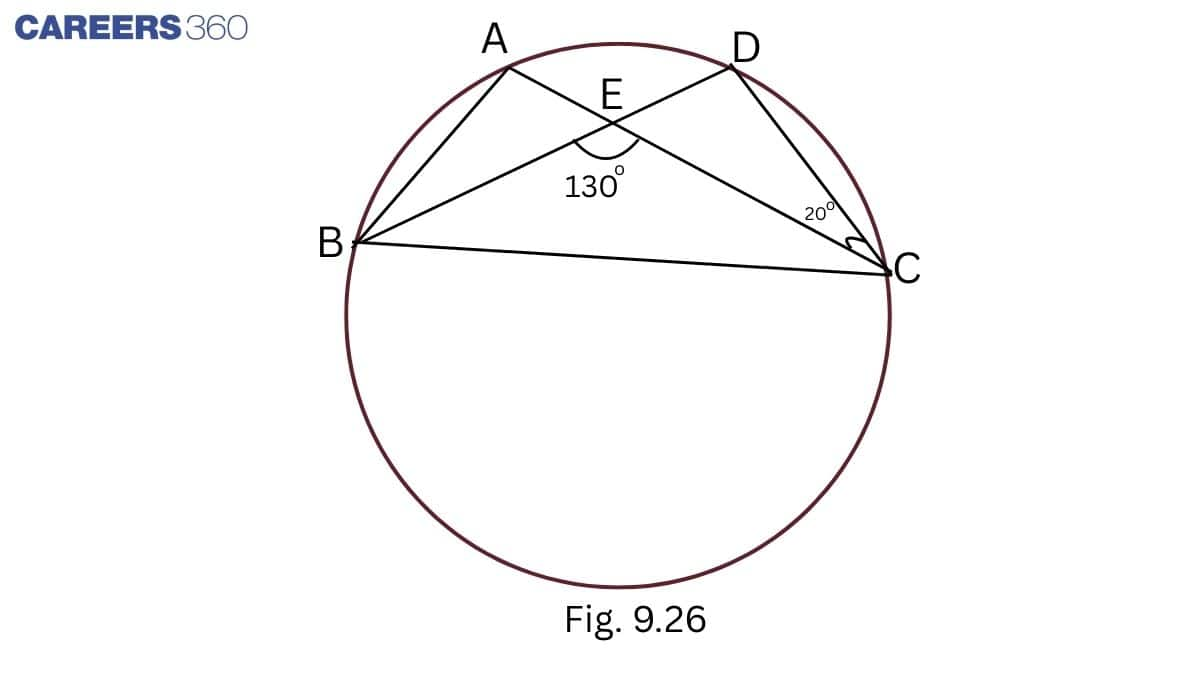 .
.
Solution:
∠ DEC+ ∠ BEC = 180∘ (linear pairs)
⇒ ∠ DEC+ 130∘ = 180∘ ( ∠ BEC = 130∘ )
⇒ ∠ DEC = 180∘ - 130∘
⇒ ∠ DEC = 50∘
In △ DEC,
∠ D+ ∠ DEC+ ∠ DCE = 180∘
⇒∠D+50∘+20∘=180∘
⇒∠D+70∘=180∘
⇒∠D=180∘−70∘=110∘
∠ D = ∠ BAC (angles in same segment are equal )
∠ BAC = 110∘
Solution: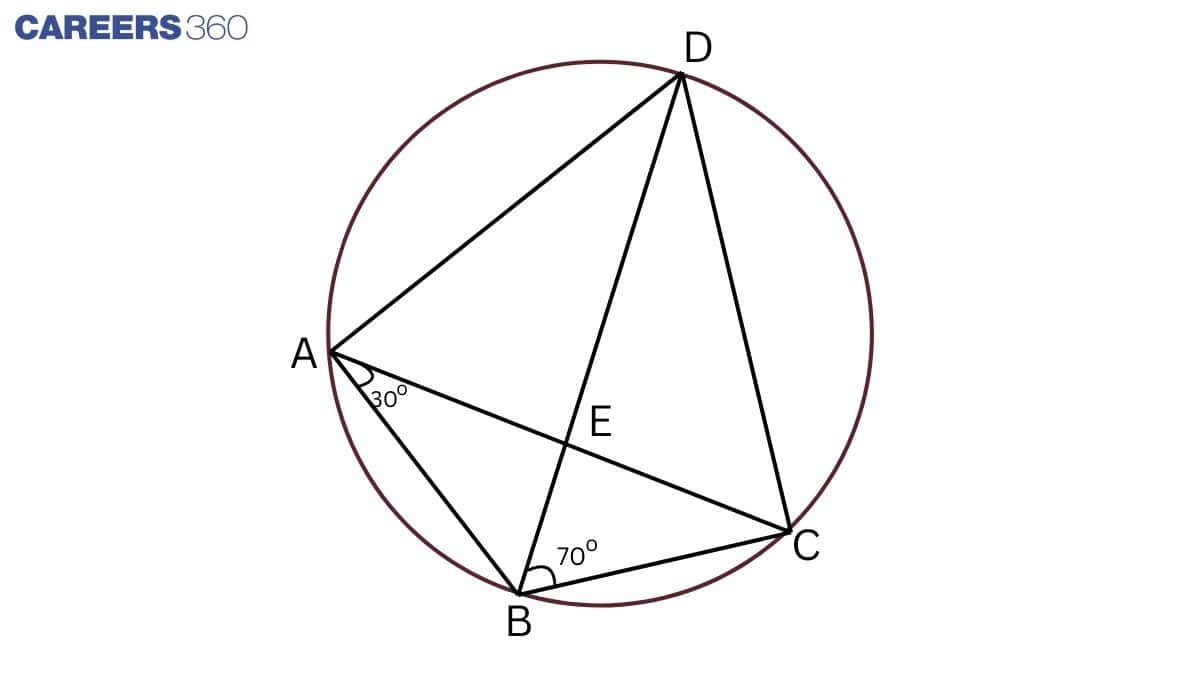
∠BDC=∠BAC (angles in the same segment are equal )
∠BDC=30∘
In △BDC,
∠BCD+∠BDC+∠DBC=180∘
⇒∠BCD+30∘+70∘=180∘
⇒∠BCD+100∘=180∘
⇒∠BCD=180∘−100∘=80∘
If AB = BC ,then
∠BCA=∠BAC
⇒∠BCA=30∘
Here, ∠ECD+∠BCE=∠BCD
⇒∠ECD+30∘=80∘
⇒∠ECD=80∘−30∘=50∘
Solution: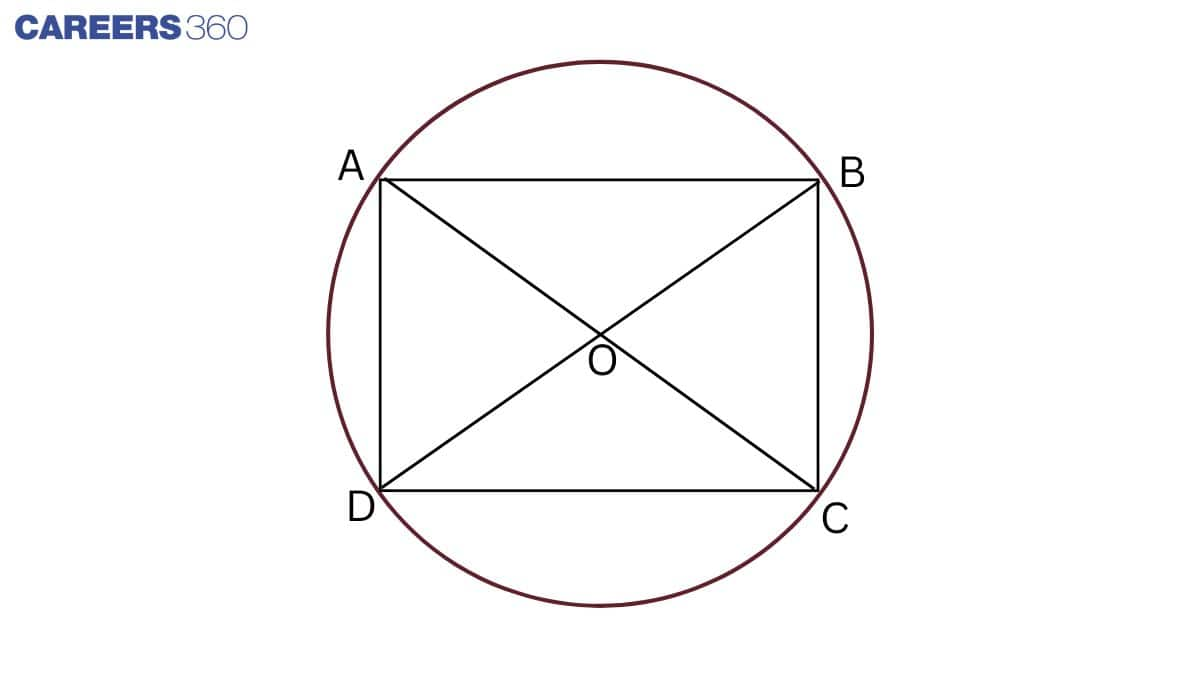
AC is the diameter of the circle.
Thus, ∠ADC=90∘ and ∠ABC=90∘ ............................1(Angle in a semi-circle is a right angle)
Similarly, BD is the diameter of the circle.
Thus, ∠BAD=90∘ and ∠BCD=90∘ ............................2(Angle in a semi-circle is a right angle)
From 1 and 2, we get
∠BCD=∠ADC=∠ABC=∠BAD=90∘
Hence, ABCD is a rectangle.
Q8 If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution: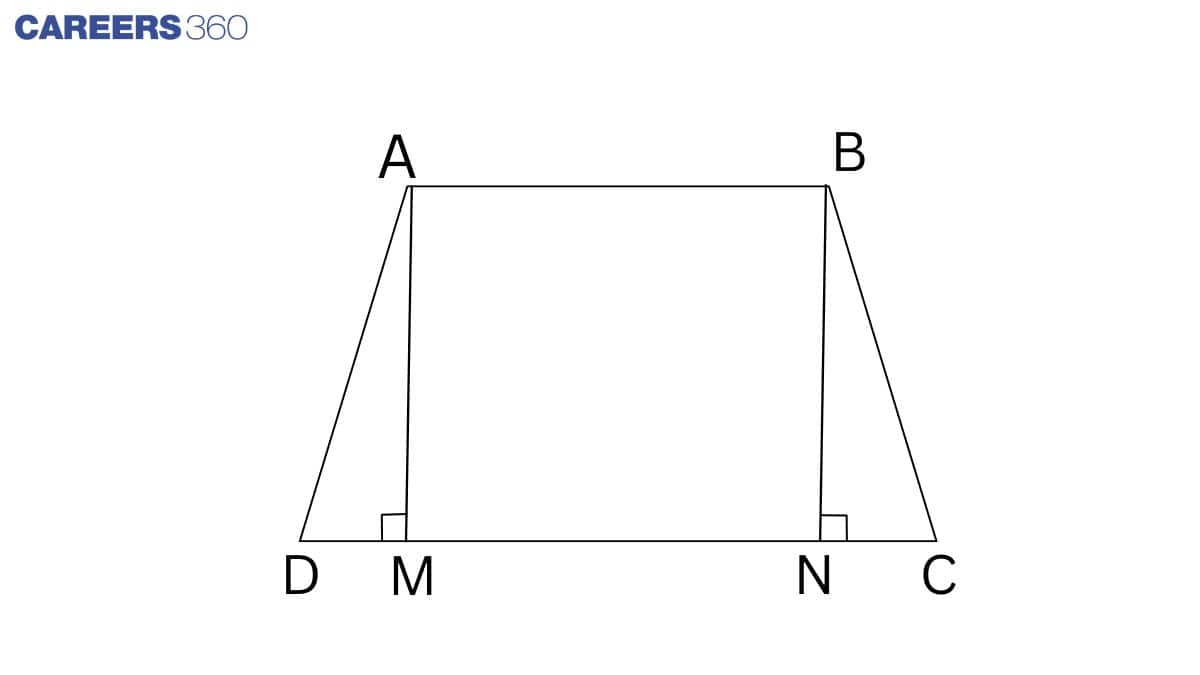
Given: ABCD is a trapezium.
Construction: Draw AD || BE.
Proof: In quadrilateral ABED,
AB || DE (Given )
AD || BE ( By construction )
Thus, ABED is a parallelogram.
AD = BE (Opposite sides of parallelogram )
AD = BC (Given )
so, BE = BC
In △ EBC,
BE = BC (Proved above )
Thus, ∠C=∠2 ...........1(angles opposite to equal sides )
∠A=∠1 ...............2(Opposite angles of the parallelogram )
From 1 and 2, we get
∠1+∠2=180∘ (linear pair)
⇒∠A+∠C=180∘
Thus, ABED is a cyclic quadrilateral.
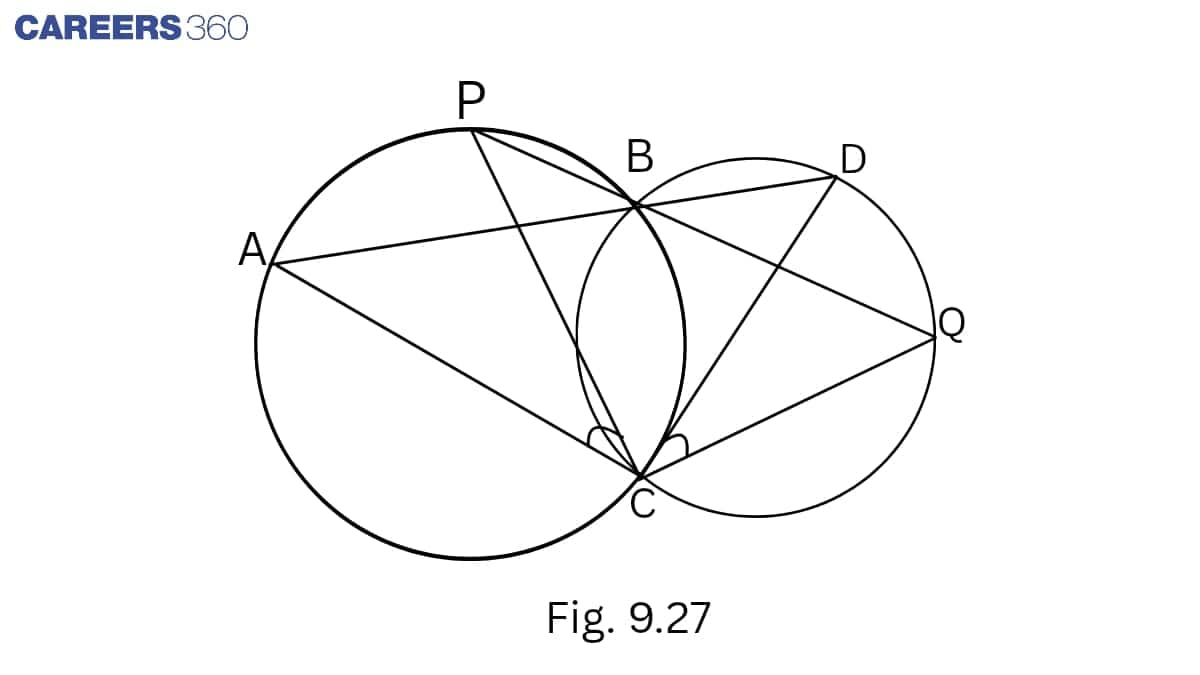
Solution:
∠ABP=∠QBD ................1(vertically opposite angles)
∠ACP=∠ABP ..................2(Angles in the same segment are equal)
∠QBD=∠QCD .................3(angles in the same segment are equal)
From 1,2,3 ,we get
∠ACP=∠QCD
Answer:
Given: circles are drawn taking two sides of a triangle as diameters.
Construction: Join AD.
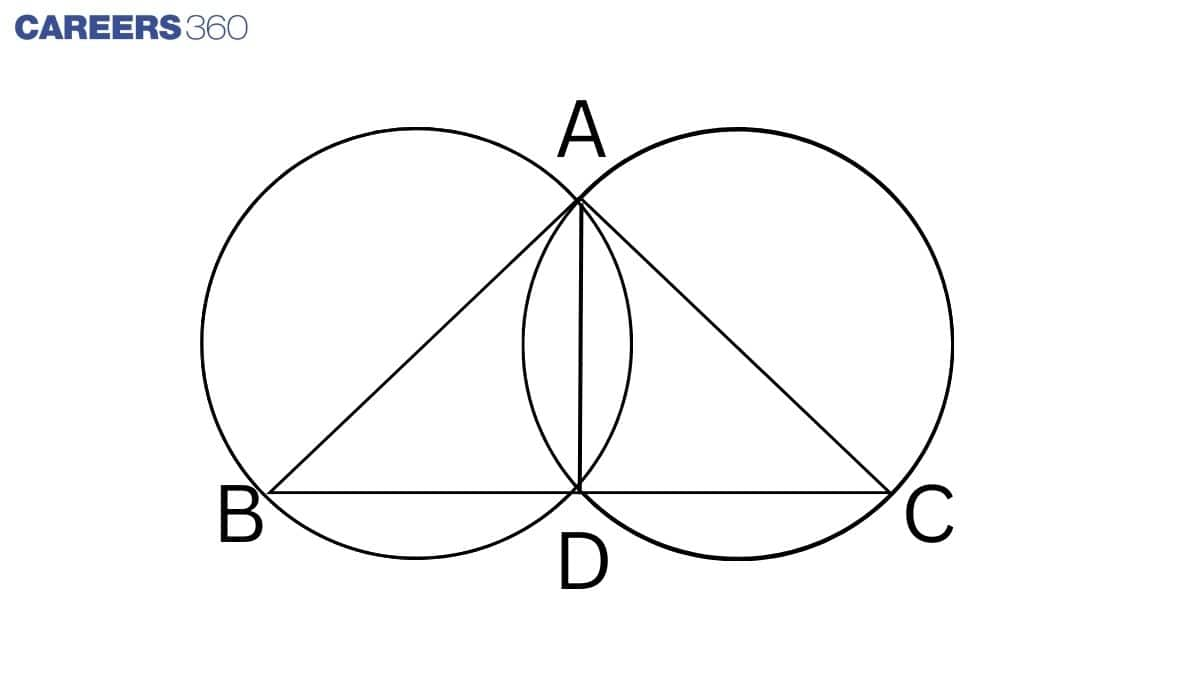
Proof: AB is the diameter of the circle and ∠ ADB is formed in a semi-circle.
∠ ADB = 90∘ ........................1(angle in a semi-circle)
Similarly,
AC is the diameter of the circle and ∠ ADC is formed in a semi-circle.
∠ ADC = 90∘ ........................2(angle in a semi-circle)
From 1 and 2, we have
∠ ADB+ ∠ ADC= 90∘ + 90∘ = 180∘
∠ ADB and ∠ ADC are forming a linear pair. So, BDC is a straight line.
Hence, point D lies on this side.
Q11 ABC and ADC are two right triangles with common hypotenuse AC. Prove that
∠CAD=∠CBD .
Solution:
Given: ABC and ADC are two right triangles with common hypotenuse AC.
To prove : ∠CAD=∠CBD
Proof :
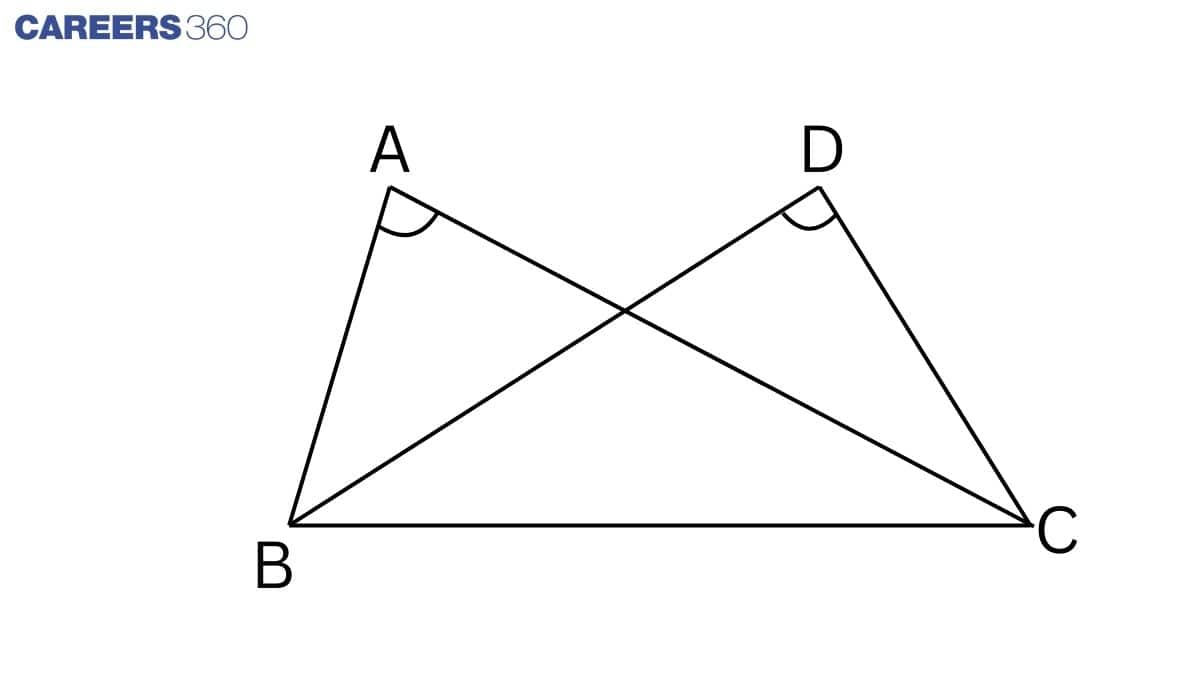
Triangle ABC and ADC are on common base BC and ∠ BAC = ∠ BDC.
Thus, point A, B, C, D lie in the same circle.
(If a line segment joining two points subtends equal angles at two other points lying on the same side of line containing line segment, four points lie on the circle.)
∠ CAD = ∠ CBD (Angles in the same segment are equal)
Q12 Prove that a cyclic parallelogram is a rectangle.
Solution:
Given: ABCD is a cyclic quadrilateral.
To prove: ABCD is a rectangle.
Proof :
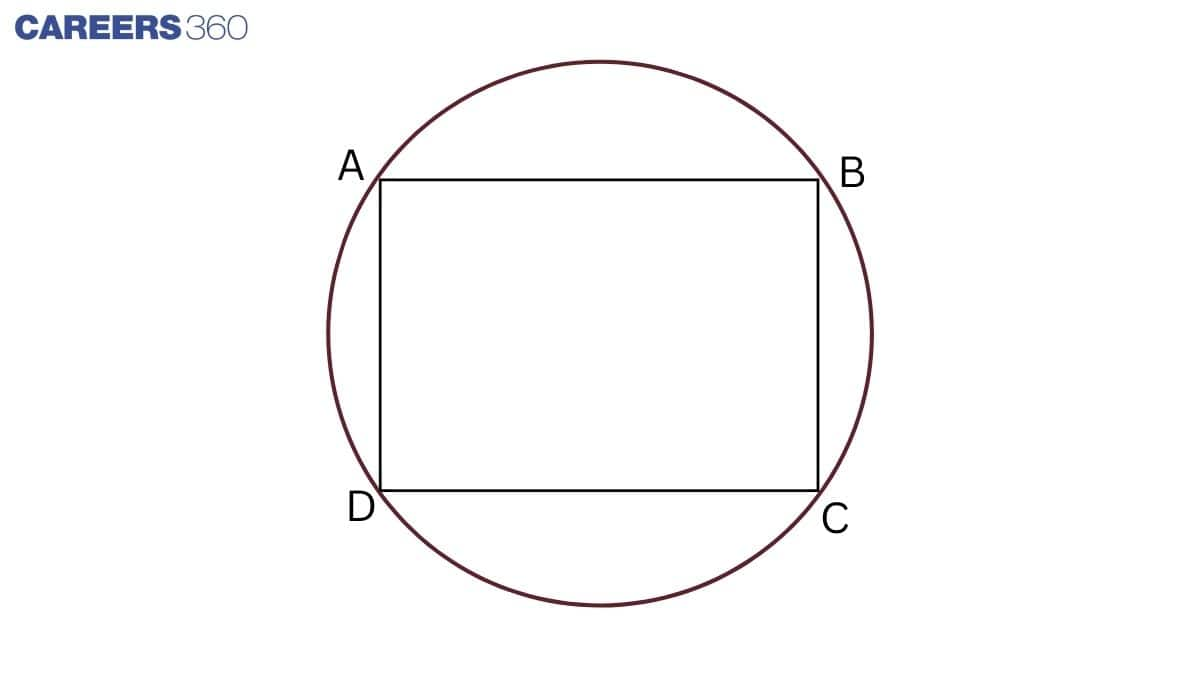
In cyclic quadrilateral ABCD.
∠A+∠C=180∘ .......................1(sum of either pair of opposite angles of a cyclic quadrilateral)
∠A=∠C ........................................2(opposite angles of a parallelogram are equal )
From 1 and 2,
∠A+∠A=180∘
⇒2∠A=180∘
⇒∠A=90∘
We know that a parallelogram with one angle a right angle is a rectangle.
Hence, ABCD is a rectangle.
Also Read:
Topics Covered in Chapter 9 Circles: Exercise 9.3
1. This exercise 9.3 class 9 maths includes some important points like when two circle chords are equal, their corresponding arcs are congruent, and when two arcs are congruent, their corresponding chords are equal.
2. A circle's congruent arcs (or equal arcs) subtend equal angles at the centre.
3. The angle of an arc at its centre is double that of any point on the circle's remainder.
4. If all four vertices of a quadrilateral ABCD lie on a circle, it is called cyclic.
5. The sum of any pair of opposite angles of a cyclic quadrilateral is 180°.
6. If a quadrilateral's sum of opposite angles is 180°, the quadrilateral is cyclic.
Also, See
NCERT Solutions of Class 9 Subject Wise
Students must check the NCERT solutions for Class 9 Maths and Science given below:
NCERT Subject-Wise Exemplar Solutions
Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:
Frequently Asked Questions (FAQs)
The quadrilateral with all of its vertices on the same circle is known as a cyclic quadrilateral.
If the sum of opposite angles in a quadrilateral is 180 degrees, the quadrilateral is said to be cyclic.
Diameter subtends right angle.
A circle divides the plane into 3 parts.
Circles should have the same radius.
Only one circle can pass through 3 noncollinear points.
The diameter is double the radius.
A segment is defined as the region between an arc and the chord of the circle.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
