NCERT Solutions for Class 9 Maths Chapter 9 Circles
Have you ever tossed a coin, seen how beautiful the full moon looks in the night sky, or ordered a delicious pizza? So many things around us are round in shape; all of these round objects are examples of circles, an essential part of geometry. The chapter Circles of the NCERT Syllabus of Class 9 Maths includes the properties of circles, arcs, tangents, chords, and their distances from the centre, cyclic quadrilaterals, etc. These key concepts of circles will help the students understand more advanced geometry concepts effectively and enhance their problem-solving ability in real-world applications. The primary benefit of NCERT Solutions for Class 9 is that they provide clear explanations, making learning simpler and more effective.
This Story also Contains
- Circles Class 9 Question And Answers PDF Free Download
- NCERT Solutions for Class 9 Maths Chapter 9 Circles: Exercise Questions
- Circles Class 9 NCERT Solutions: Exercise-wise
- Class 9 Maths NCERT Chapter 9: Extra Question
- Circles Class 9 Chapter 9: Topics
- Circles Class 9 Solutions - Important Formulae And Points
- Approach to Solve Questions of Circles Class 9
- Why are Class 9 Maths Chapter 9 Circles Question Answers Important?
- NCERT Solutions For Class 9 Maths Chapter Wise

Every student must understand circles to do well in geometry. Understanding the figures and proofs of the theorems of circles makes it easy to score marks in the exam. These NCERT Solutions for Class 9 Maths are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. Students who need the Circles Class 9 solutions will find this article very useful. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus. Explore NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions for complete syllabus coverage in this NCERT article.
Circles Class 9 Question And Answers PDF Free Download
Careers360 brings you NCERT Solutions for Class 9 Maths Chapter 9 Circles, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 9 Maths Chapter 9 Circles: Exercise Questions
NCERT Class 9 Maths Chapter 9 Circles question answers with detailed explanations are provided below.
|
Circles Class 9 Question Answers Exercise: 9.1 Total Questions: 2 Page number: 118 |
Answer:
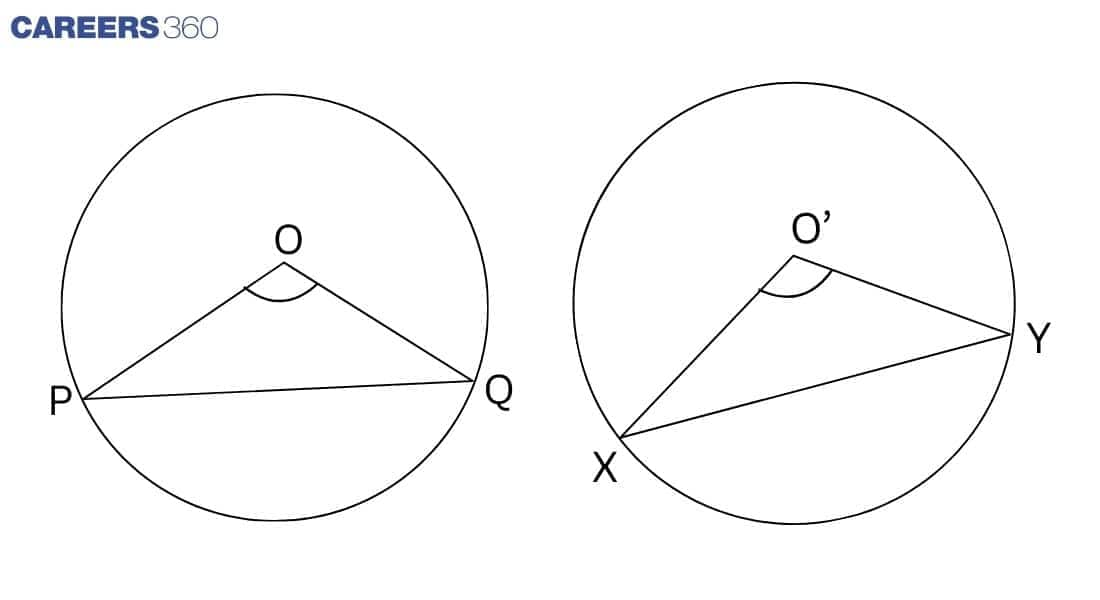
In the given figure, two congruent circles are given and have centres O and O', and chords are PQ and XY, respectively.
In Δ POQ and XO'Y
PQ = XY (Given)
OP = O'X (Radius of congruent triangle)
OQ = O'Y (Radius of congruent triangle)
ΔPOQ ≅ ΔXO'Y (By SSS rule)
Therefore, ∠POQ = ∠XO'Y (By CPCT)
Question 2: Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:
Given: Two congruent circles have equal angles.
To Prove: Two congruent circles have equal angles, and then the chords are equal.
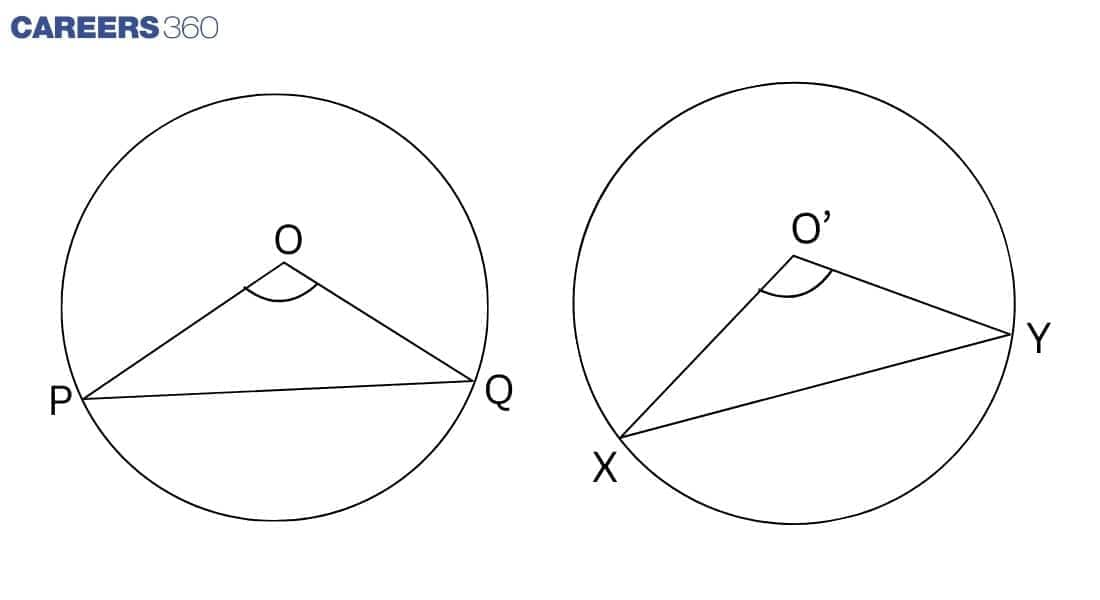
In Δ POQ and XO'Y
∠POQ = ∠XO'Y (Given)
OP = O'X (Radius of a congruent triangle)
OQ = O'Y (Radius of congruent triangle)
ΔPOQ ≅ ΔXO'Y (By SSS rule)
Therefore, PQ = XY (By CPCT)
|
Circles Class 9 Question Answers Exercise: 9.2 Total Questions: 6 Page number: 122 |
Given: Two circles of radii $\small 5\hspace{1mm}cm$ and $\small 3\hspace{1mm}cm$ intersect at two points and the distance between their centres is $\small 4\hspace{1mm}cm$.
To find the length of the common chord.
Construction: Join OP and ON, draw $OM\perp AB\
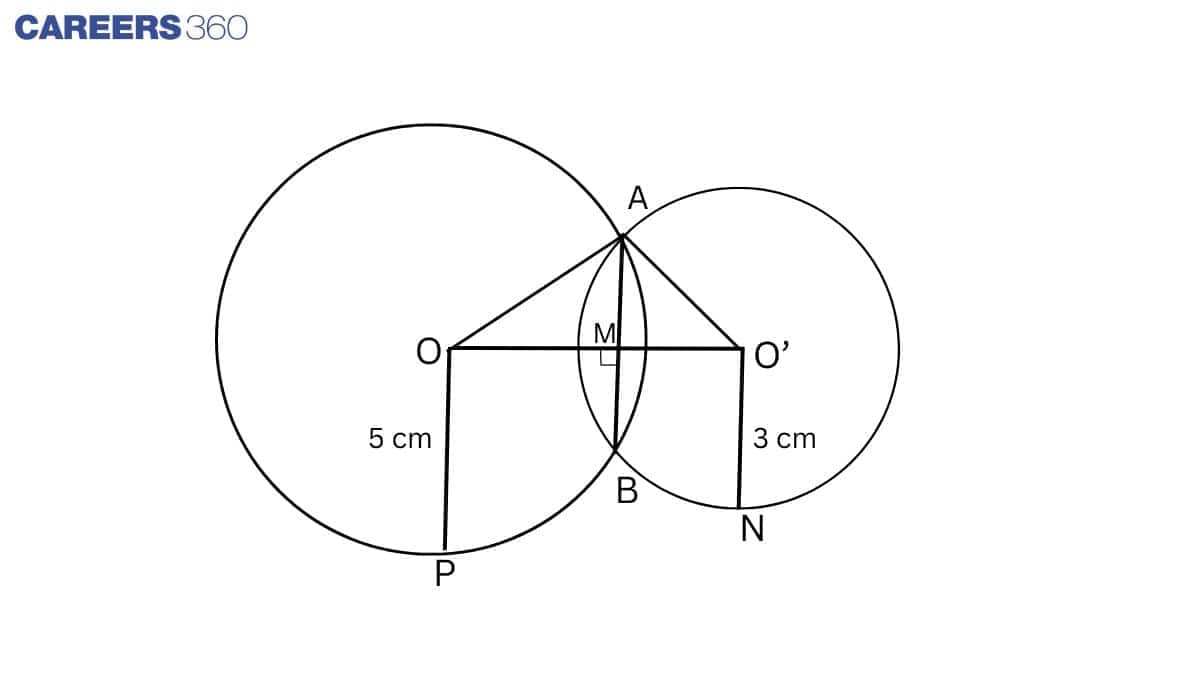
Proof: AB is a chord of the circle, and OM is the bisector of chord AB.
$\therefore OM\perp AB$
$\angle OMA = 90 ^\circ$
Let, OM = x , so O'M = 4 - x
In $\triangle$ AOM, using Pythagoras' theorem
$AM^2=AO^2 - OM^2$ ...........................(1)
Also,
In $\triangle$ AO'M, using Pythagoras' theorem
$AM^2=AO'^2 - MO'^2$ ...........................(2)
From (1) and (2), we get
$AO^2 - OM^2 = AO'^2 - MO'^2$
$\Rightarrow 5^2 - x^2 = 3^2 - (4 - x)^2$
$\Rightarrow 25 - x^2 = 9 - 16 - x^2 + 8x$
$\Rightarrow 32 = 8x$
$\Rightarrow x = 4$
Put x = 4 in equation (1)
$AM^2 = 5^2 - 4^2 = 9$
$\Rightarrow AM = 3$
$\Rightarrow AB = 2AM = 6$
Question 2: If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to the corresponding segments of the other chord.
Answer:
Given: two equal chords of a circle intersect within the circle.
To prove: Segments of one chord are equal to corresponding segments of the other chord, i.e. AP = CP and BP = DP.
Construction: Join OP and draw $OM\perp AB\, \, \, \, and\, \, \, ON\perp CD.$
Proof:
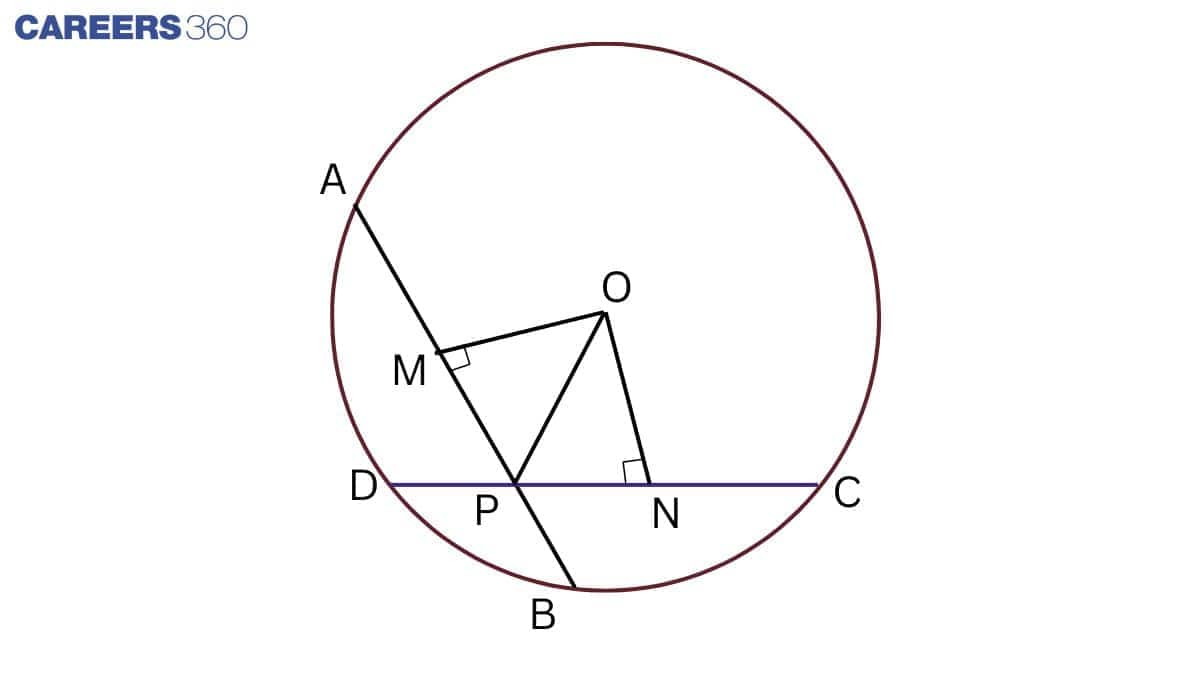
In $\triangle$ OMP and $\triangle$ ONP,
OP = OP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
$\angle$ OMP = $\angle$ ONP (Both are right angled)
Thus, $\triangle$ OMP $\cong$ $\triangle$ ONP (By SAS rule)
PM = PN..........................(1) (CPCT)
AB = CD ..........................(2)(Given)
$\Rightarrow \frac{1}{2}AB=\frac{1}{2}CD$
$\Rightarrow AM = CN$ .....................(3)
Adding equations (1) and (3), we have
AM + PM = CN + PN
$\Rightarrow AP = CP$ .................(4)
Subtract equation (4) from (2), we get
$ AB - AP = CD - CP$
$\Rightarrow PB = PD$
Question 3: If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
Given: two equal chords of a circle intersect within the circle.
To prove: the line joining the point of intersection to the centre makes equal angles with the chords.
i.e. $\angle$ OPM= $\angle$ OPN
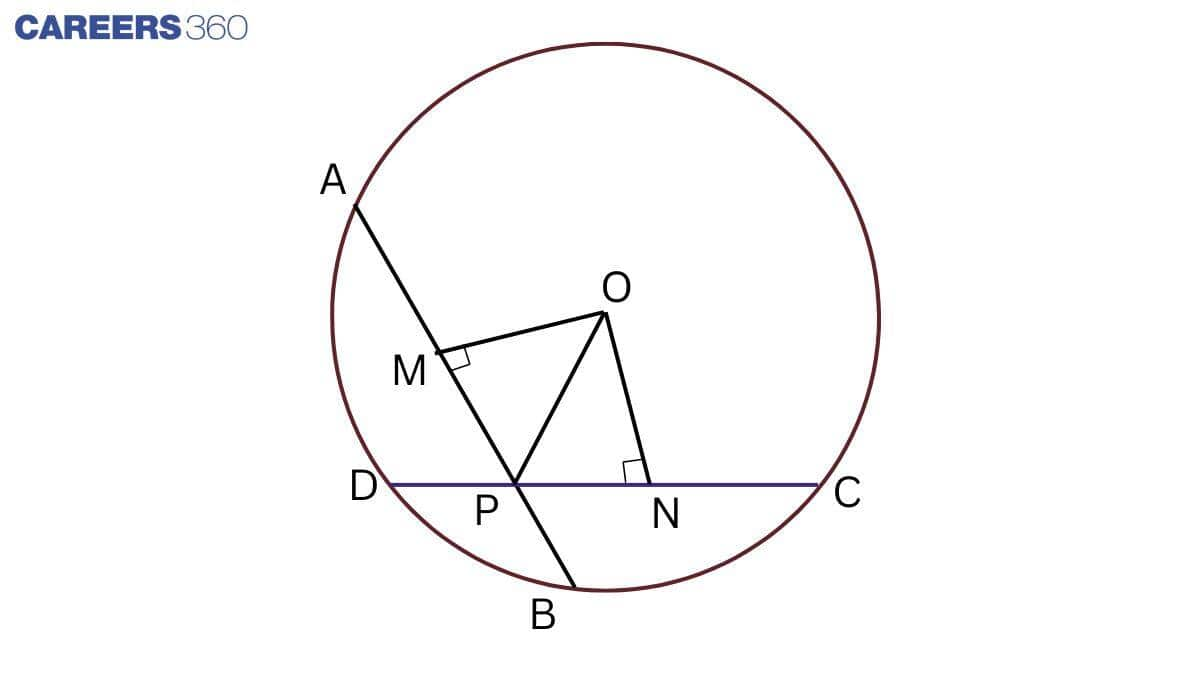
Proof:
Construction: Join OP and draw $OM\perp AB\, \, \, \, and\, \, \, ON\perp CD.$
In $\triangle$ OMP and $\triangle$ ONP,
OP = OP (Common)
OM = ON (Equal chords of a circle are equidistant from the centre)
$\angle$ OMP = $\angle$ ONP (Both are right-angled)
Thus, $\triangle$ OMP $\cong$ $\triangle$ ONP (By RHS rule)
$\angle$ OPM= $\angle$ OPN (CPCT)
Answer:
Given: a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D.
To prove: AB = CD
Construction: Draw $OM\perp AD$
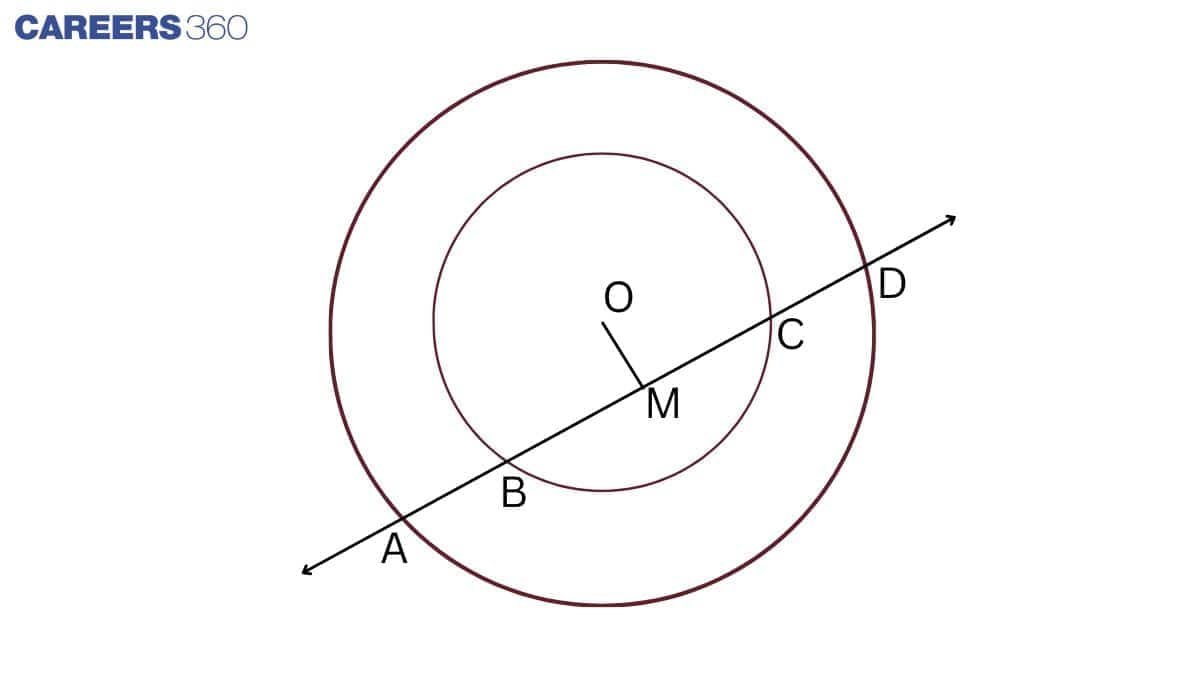
BC is a chord of the inner circle, and $OM\perp BC$
So, BM = CM .................(1)
(Perpendicular OM bisect BC)
Similarly,
AD is a chord of the outer circle, and $OM\perp AD$
So, AM = DM .................(2) (Perpendicular OM bisect AD)
Subtracting equation (1) from (2), we get
$ AM-BM = DM - CM$
$\Rightarrow AB = CD$
Answer:
Given: From the figure, R, S, and M are the positions of Reshma, Salma, and Mandip, respectively.
So, RS = SM = 6 cm
Construction: Join ON, OS, OR and OM. Draw $OL\perp RS$.
Proof:
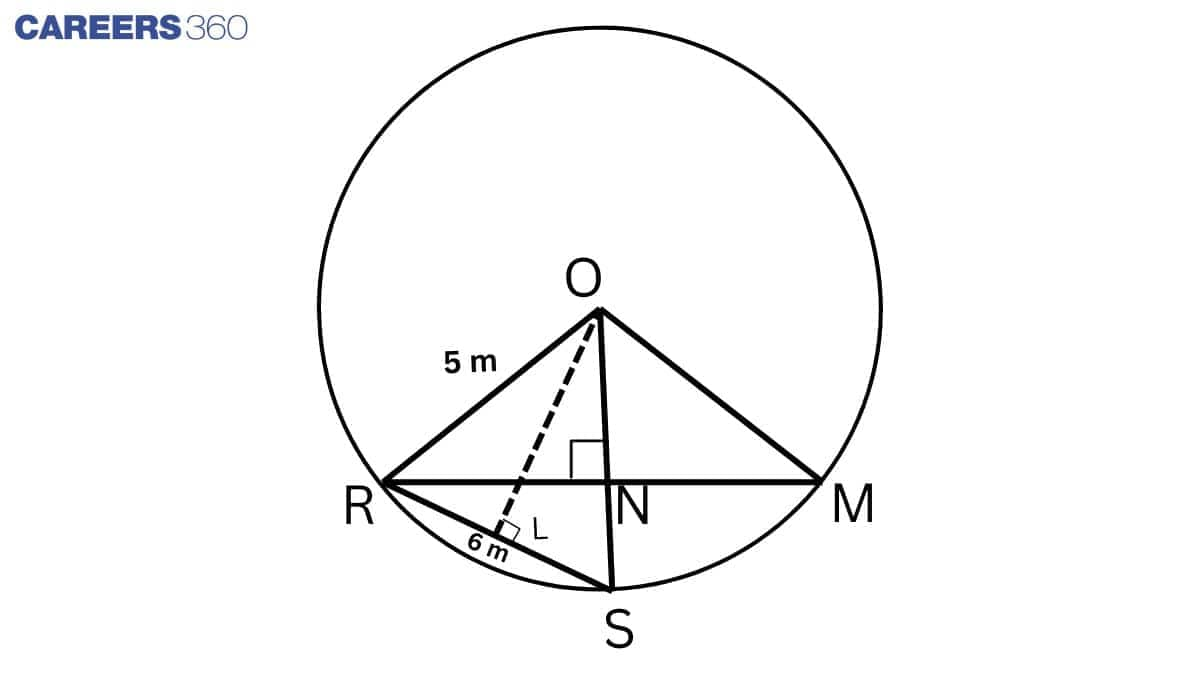
In $\triangle$ ORS,
OS = OR and $OL\perp RS$ (by construction)
So, RL = LS = 3cm (RS = 6 cm)
In $\triangle$ OLS, by Pythagoras' theorem,
$OL^2 = OS^2 - SL^2$
$\Rightarrow OL^2 = 5^2 - 3^2 = 25 - 9 = 16$
$\Rightarrow OL = 4$
In $\triangle$ ORN and $\triangle$ OMN,
OR = OM (Radii)
$\angle$ RON = $\angle$ MON (Equal chords subtend equal angles at the centre)
ON = ON (Common)
$\triangle$ ORN $\cong$ $\triangle$ OMN (By SAS)
RN = MN (CPCT)
Thus, $ON\perp RM$
Area of $\triangle$ ORS = $\frac{1}{2}\times RS\times OL$ ..................(1)
Area of $\triangle$ ORS = $\frac{1}{2}\times OS\times NR$ ..................(2)
From 1 and 2, we get
$\frac{1}{2}\times RS\times OL$ $ = \frac{1}{2}\times OS\times NR$
$\Rightarrow RS\times OL= OS\times KR$
$\Rightarrow 6\times 4 = 5\times KR$
$\Rightarrow NR = 4.8 cm$
Thus, $RM =2 NR = 2\times 4.8 cm = 9.6 cm$
Answer:
Given: In the figure, A, B, and C are positioned as Ankur, Syed and David, respectively.
So, AB = BC = CD
Radius of circular park = 20m
So, AO = OB = OC = 20m
Construction: AF $\perp$ BC
Proof:
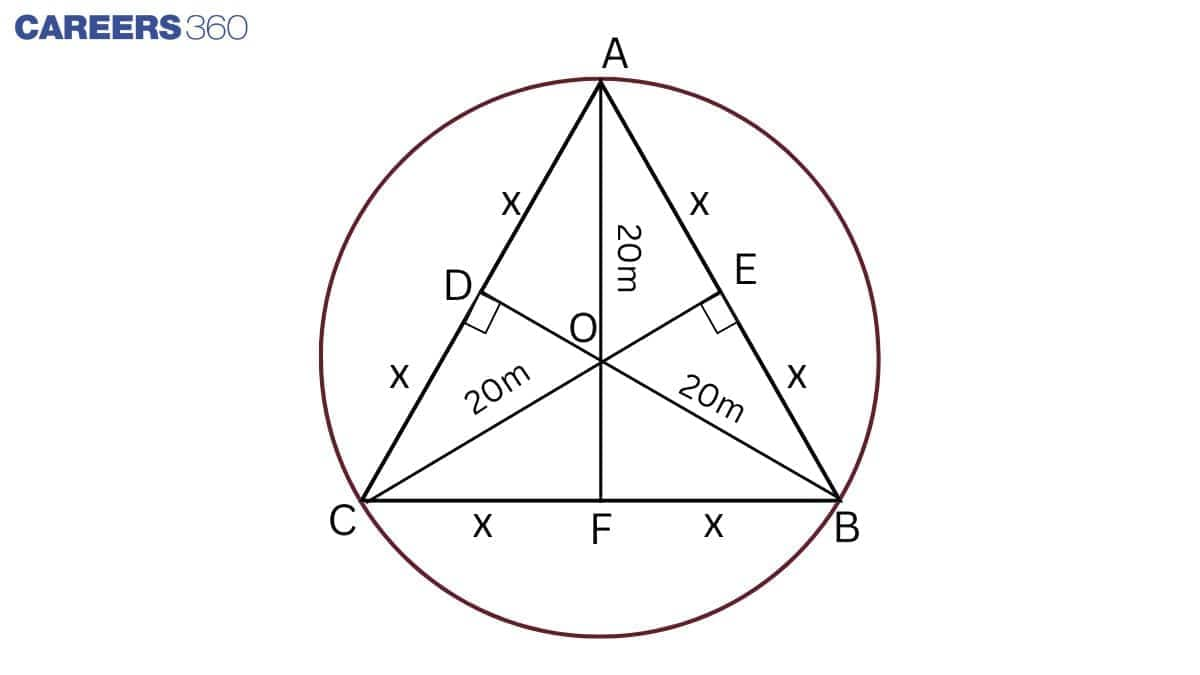
Let AC = CB = AB = 2x cm
In $\triangle$ ABC,
AC = AB and AF $\perp$ BC
So, CF = FB = x cm
In $\triangle$ OFB, by Pythagoras,
$OF^2=OB^2-FB^2$
$\Rightarrow OF^2 = 20^2-x^2 = 400-x^2$
$\Rightarrow OF = \sqrt{400-x^2}$
In $\triangle$ AFB, by Pythagoras,
$AF^2 = AB^2-FB^2$
$\Rightarrow (AO+OF)^2 + x^2 = (2x)^2$
$\Rightarrow (20+\sqrt{400 - x^2})^2 + x^2 = 4x^2$
$\Rightarrow 400 + 400 - x^2 + 40\sqrt{400 - x^2} + x^2 = 4x^2$
$\Rightarrow 800 + 40\sqrt{400 - x^2} = 4x^2$
$\Rightarrow 200 + 10\sqrt{400 - x^2} = x^2$
$\Rightarrow 10\sqrt{400 - x^2} = x^2 - 200$
Squaring both sides,
$\Rightarrow 100(400 - x^2) = (x^2 - 200)^2$
$\Rightarrow 40000 - 100x^2 = x^4-40000 - 400x^2$
$\Rightarrow x^4 - 300x^2 = 0$
$\Rightarrow x^2(x^2 - 300) = 0$
$\Rightarrow x^2 = 300$
$\Rightarrow x = 10\sqrt{3}$
Hence, the length of the string of each phone $= 2x = 20\sqrt{3}$ m
|
Circles Class 9 Question Answers Exercise: 9.3 Total Questions: 12 Page number: 127-129 |

Answer:
$\angle$ AOC = $\angle$ AOB + $\angle$ BOC = $60 ^\circ+30 ^\circ=90 ^\circ$
$\angle$ AOC = 2 $\angle$ ADC (angle subtended by an arc at the centre is double the angle subtended by it at any point)
$\angle ADC = \frac{1}{2}\angle AOC$
$\Rightarrow \angle ADC=\frac{1}{2}\times 90 ^\circ = 45 ^\circ$
Answer:
Given: A chord of a circle is equal to the radius of the circle, i.e. OA = AB.
To find: $\angle$ADB and $\angle$ ACB.
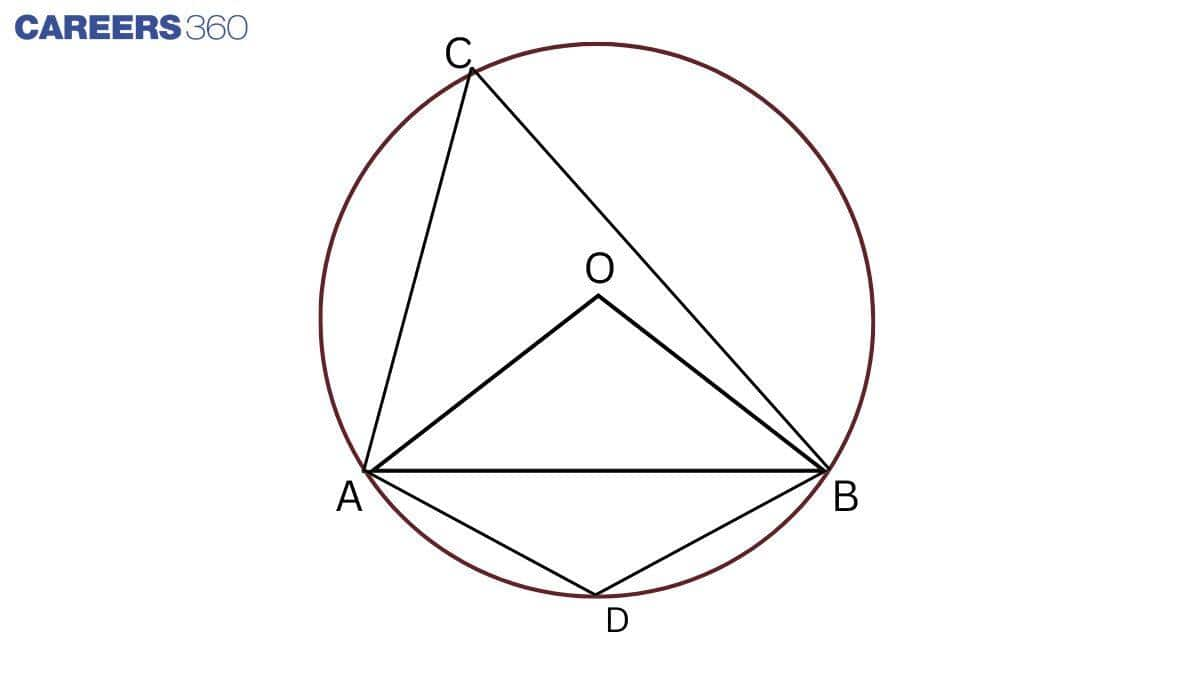
In $\triangle$ OAB,OA = AB (Given)
OA = OB (Radii of circle)
So, OA = OB = AB
$\Rightarrow$ AOB is an equilateral triangle.
So, $\angle$ AOB = $60 ^\circ$
$\angle$ AOB = 2 $\angle$ ADB
$\Rightarrow \angle ADB = \frac{1}{2}\angle AOB$
$\Rightarrow \angle ADB = \frac{1}{2} \times 60 ^\circ=30$
ACBD is a cyclic quadrilateral.
So, $\angle$ ACB+ $\angle$ ADB = $180 ^\circ$
$\Rightarrow \angle ACB + 30 ^\circ= 180 ^\circ$
$\Rightarrow \angle ACB = 180 ^\circ-30 ^\circ=150 ^\circ$
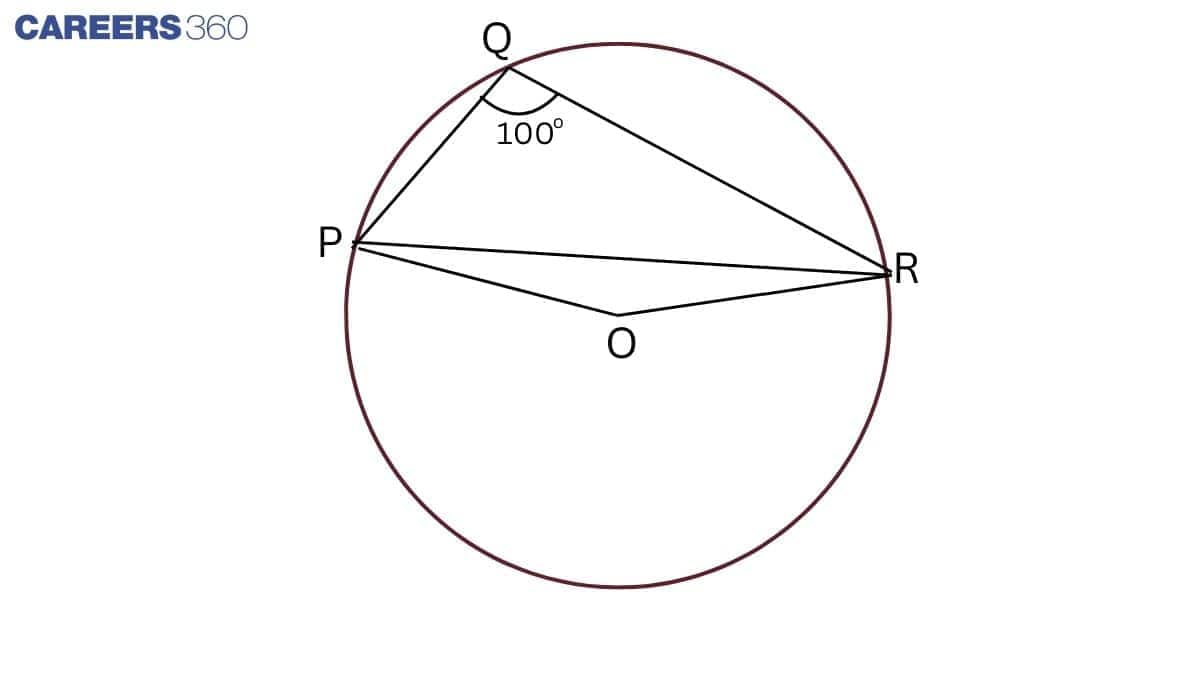
Answer:
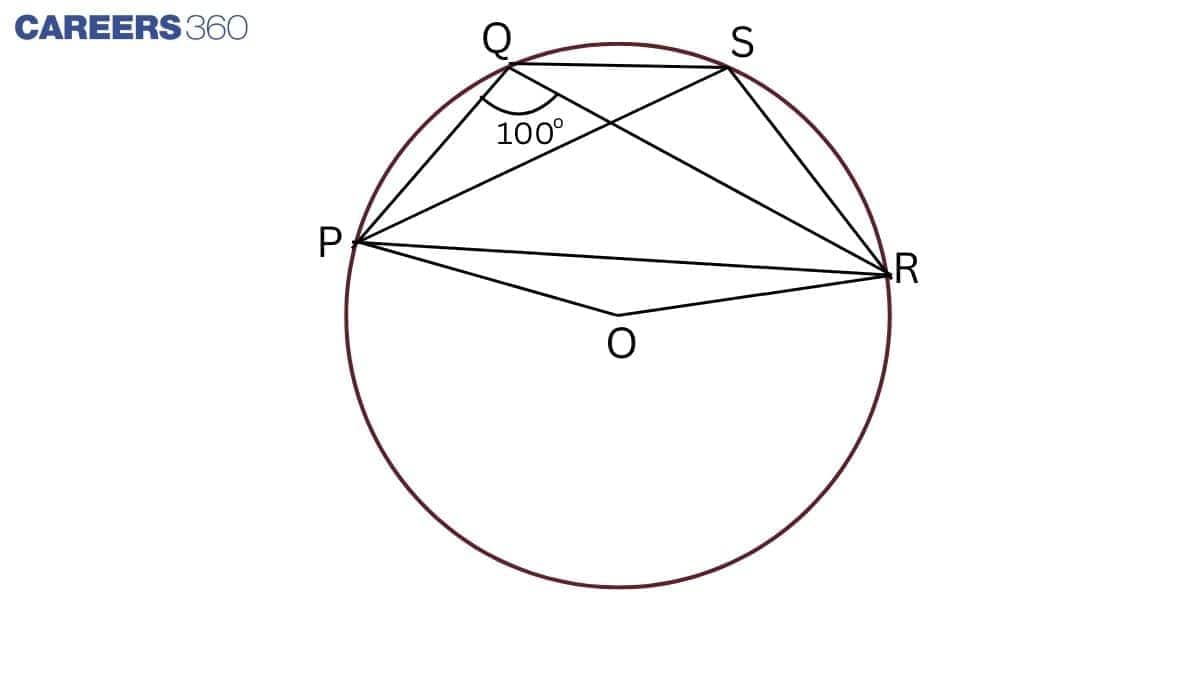
Construction: Join PO and OR.
PQSR is a cyclic quadrilateral.
So, $\angle$ PSR + $\angle$ PQR = $180 ^\circ$
$\Rightarrow \angle PSR + 100 ^\circ = 180 ^\circ$
$\Rightarrow \angle PSR = 180 ^\circ - 100 ^\circ = 80 ^\circ$
Here, $\angle$ POR = 2 $\angle$ PSR
$\Rightarrow \angle POR = 2\times 80 ^\circ = 160 ^\circ$
In $\triangle$ OPR,
OP = OR (Radii)
$\angle$ ORP = $\angle$ OPR (the angles opposite to equal sides)
In $\triangle$ OPR,
$\angle$ OPR+ $\angle$ ORP + $\angle$ POR = $180 ^\circ$
$\Rightarrow 2\angle OPR + 160 ^\circ = 180 ^\circ$
$\Rightarrow 2\angle OPR = 180 ^\circ - 160 ^\circ$
$\Rightarrow 2\angle OPR = 20 ^\circ$
$\Rightarrow \angle OPR = 10 ^\circ$
Question 4: In Fig. $\small 10.38$ , $\small \angle ABC=69^{\circ}, \angle ACB=31^{\circ},$ find $\small \angle BDC$
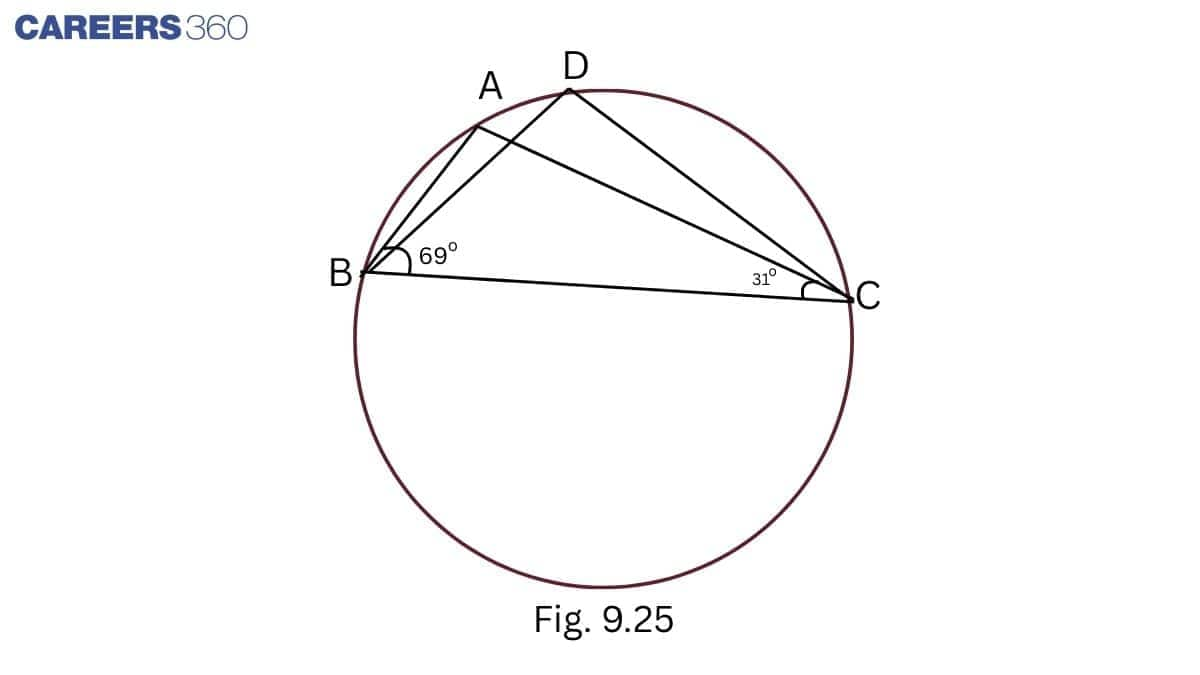
Answer:
In $\triangle$ ABC,
$\angle$ A+ $\angle$ ABC+ $\angle$ ACB= $180^\circ$
$\Rightarrow \angle A+69 ^\circ+31 ^\circ=180^\circ$
$\Rightarrow \angle A+100 ^\circ=180^\circ$
$\Rightarrow \angle A=180 ^\circ-100^\circ$
$\Rightarrow \angle A=80 ^\circ$
$\angle$ A = $\angle$ BDC = $80 ^\circ$ (Angles in same segment)
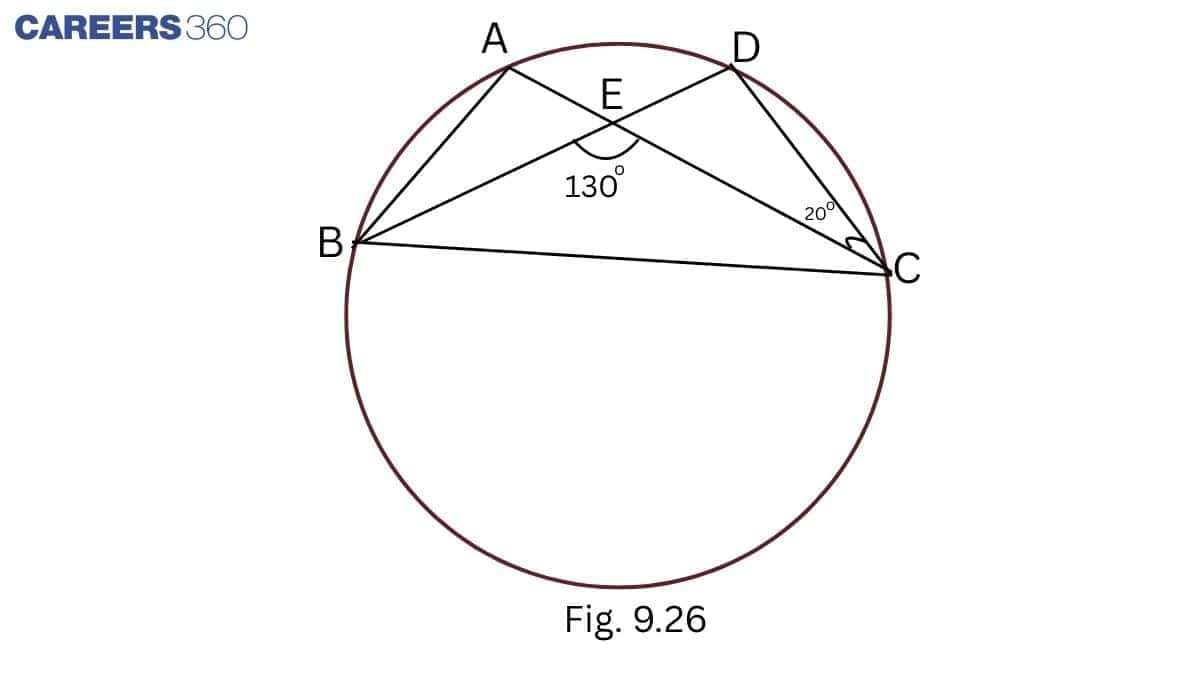
Answer:
$\angle$ DEC+ $\angle$ BEC = $180 ^\circ$ (linear pairs)
$\Rightarrow$ $\angle$ DEC+ $130 ^\circ$ = $180 ^\circ$ ( $\angle$ BEC = $130 ^\circ$ )
$\Rightarrow$ $\angle$ DEC = $180 ^\circ$ - $130 ^\circ$
$\Rightarrow$ $\angle$ DEC = $50 ^\circ$
In $\triangle$ DEC,
$\angle$ D+ $\angle$ DEC+ $\angle$ DCE = $180 ^\circ$
$\Rightarrow \angle D+50 ^\circ+20 ^\circ= 180 ^\circ$
$\Rightarrow \angle D+70 ^\circ= 180 ^\circ$
$\Rightarrow \angle D= 180 ^\circ-70 ^\circ=110 ^\circ$
$\angle$ D = $\angle$ BAC (angles in the same segment are equal )
$\angle$ BAC = $110 ^\circ$
Answer:
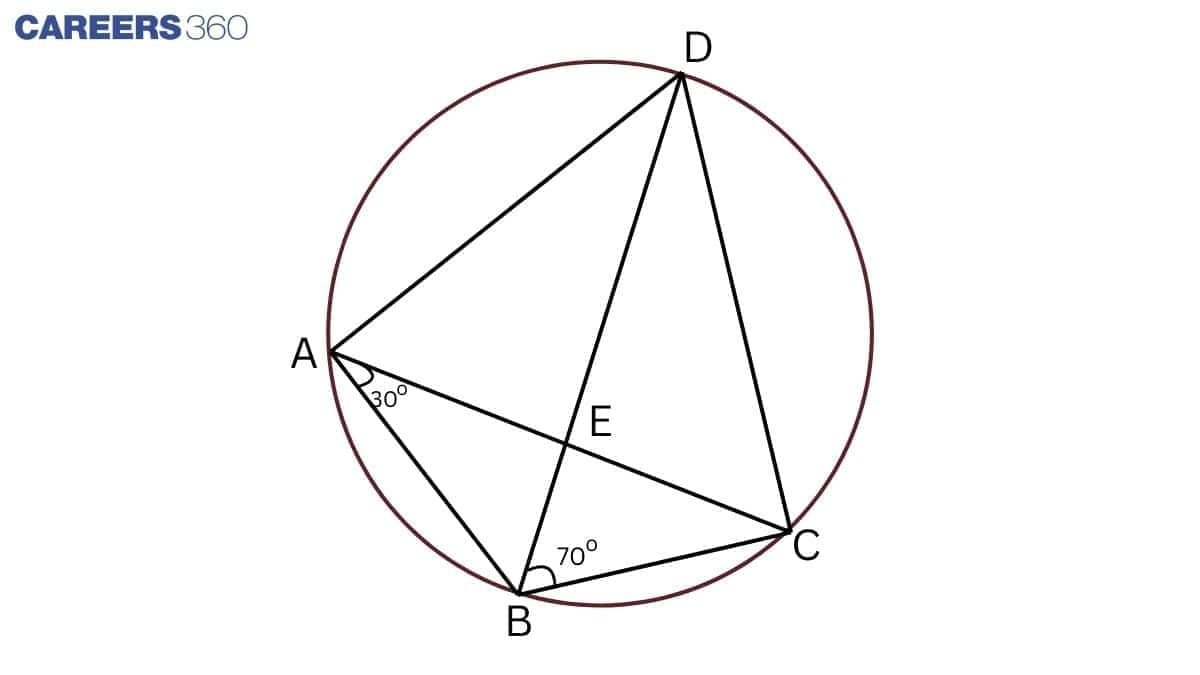
$\angle BDC=\angle BAC$ (angles in the same segment are equal )
$\angle BDC= 30 ^\circ$
In $\triangle BDC,$
$\angle BCD+\angle BDC+\angle DBC= 180 ^\circ$
$\Rightarrow \angle BCD+30 ^\circ+70 ^\circ= 180 ^\circ$
$\Rightarrow \angle BCD+100 ^\circ= 180 ^\circ$
$\Rightarrow \angle BCD=180 ^\circ- 100 ^\circ=80 ^\circ$
If AB = BC, then
$\angle BCA=\angle BAC$
$\Rightarrow \angle BCA=30 ^\circ$
Here, $\angle ECD+\angle BCE=\angle BCD$
$\Rightarrow \angle ECD+30 ^\circ=80 ^\circ$
$\Rightarrow \angle ECD=80 ^\circ-30 ^\circ=50 ^\circ$
Answer:
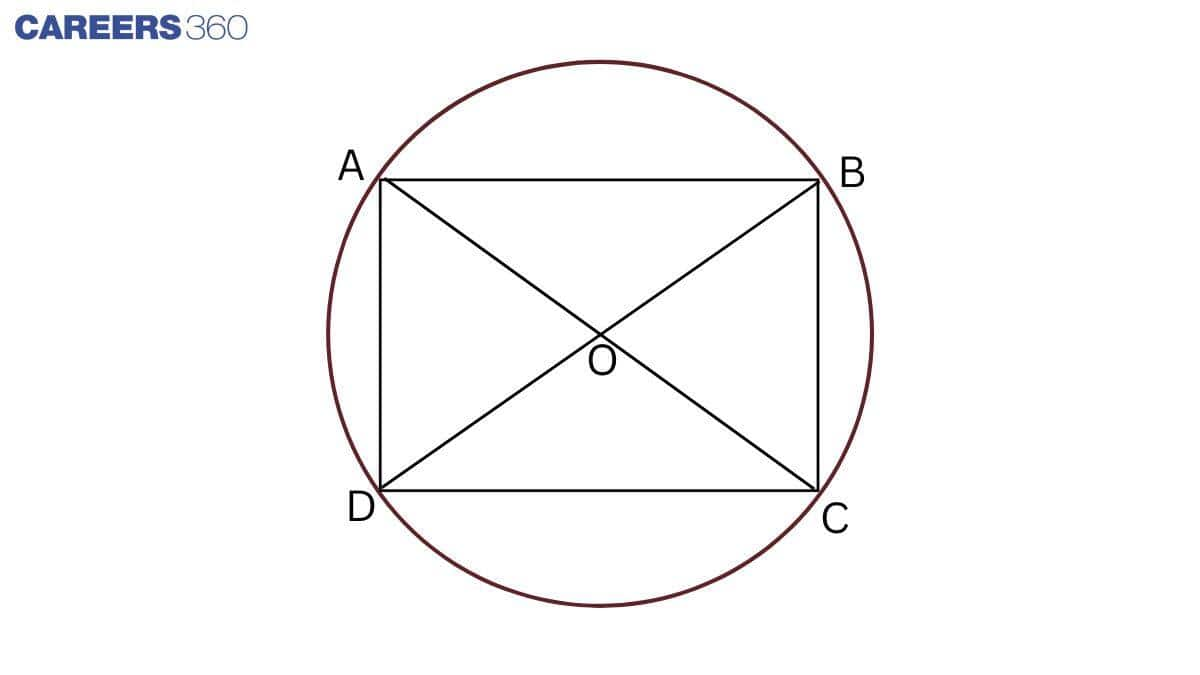
AC is the diameter of the circle.
Thus, $\angle ADC=90 ^\circ$ and $\angle ABC=90 ^\circ$ ............................1(Angle in a semi-circle is a right angle)
Similarly, BD is the diameter of the circle.
Thus, $\angle BAD=90 ^\circ$ and $\angle BCD=90 ^\circ$ ............................2(Angle in a semi-circle is a right angle)
From 1 and 2, we get
$\angle BCD=\angle ADC=\angle ABC=\angle BAD =90 ^\circ$
Hence, ABCD is a rectangle.
Question 8: If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
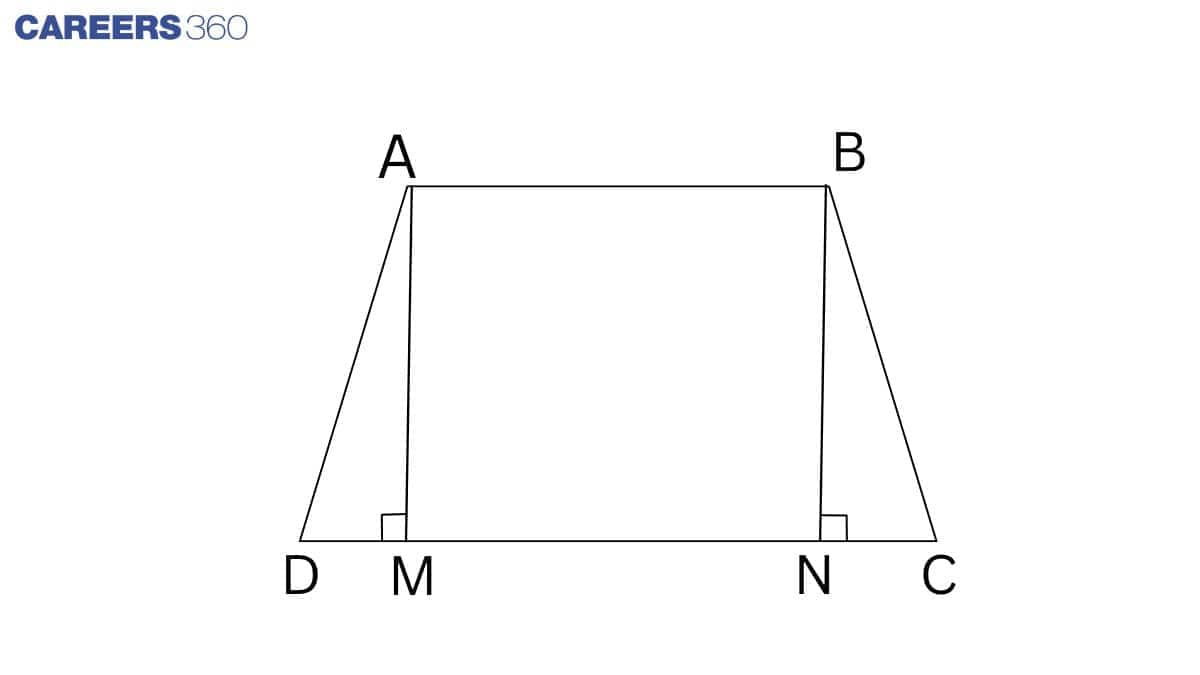
Given: ABCD is a trapezium.
Construction: Draw AD || BE.
Proof: In quadrilateral ABED,
AB || DE (Given )
AD || BE ( By construction )
Thus, ABED is a parallelogram.
AD = BE (Opposite sides of a parallelogram )
AD = BC (Given )
so, BE = BC
In $\triangle$ EBC,
BE = BC (Proved above )
Thus, $\angle C = \angle 2$ ...........1(angles opposite to equal sides )
$\angle A= \angle 1$ ...............2(Opposite angles of the parallelogram )
From 1 and 2, we get
$\angle 1+\angle 2=180 ^\circ$ (linear pair)
$\Rightarrow \angle A+\angle C=180 ^\circ$
Thus, ABED is a cyclic quadrilateral.
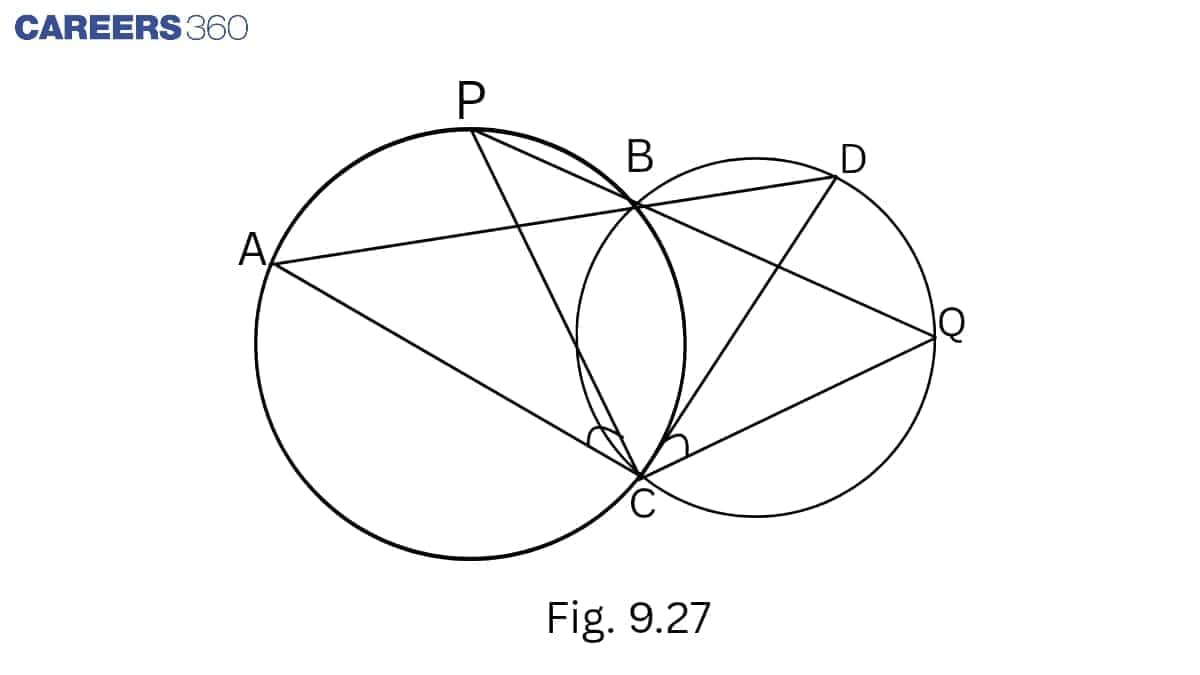
Answer:
$\angle ABP=\angle QBD$ ................1(vertically opposite angles)
$\angle ACP=\angle ABP$ ..................2(Angles in the same segment are equal)
$\angle QBD=\angle QCD$ .................3(angles in the same segment are equal)
From 1,2,3 ,we get
$\angle ACP=\angle QCD$
Answer:
Given: circles are drawn taking two sides of a triangle as diameters.
Construction: Join AD.
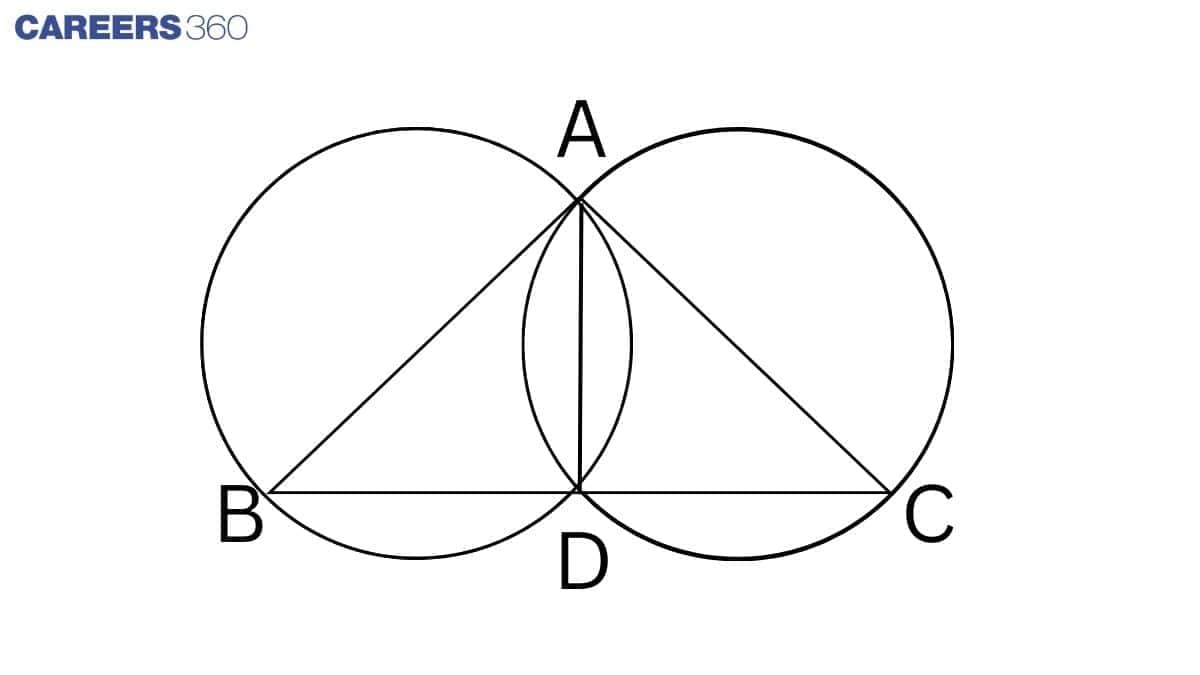
Proof: AB is the diameter of the circle, and $\angle$ ADB is formed in a semi-circle.
$\angle$ ADB = $90 ^\circ$ ........................1(angle in a semi-circle)
Similarly,
AC is the diameter of the circle, and $\angle$ ADC is formed in a semi-circle.
$\angle$ ADC = $90 ^\circ$ ........................2(angle in a semi-circle)
From 1 and 2, we have
$\angle$ ADB+ $\angle$ ADC= $90 ^\circ$ + $90 ^\circ$ = $180 ^\circ$
$\angle$ ADB and $\angle$ ADC are forming a linear pair. So, BDC is a straight line.
Hence, point D lies on this side.
Question 11: ABC and ADC are two right triangles with common hypotenuse AC. Prove that $\small \angle CAD =\angle CBD$.
Answer:
Given: ABC and ADC are two right triangles with common hypotenuse AC.
To prove : $\small \angle CAD =\angle CBD$
Proof:
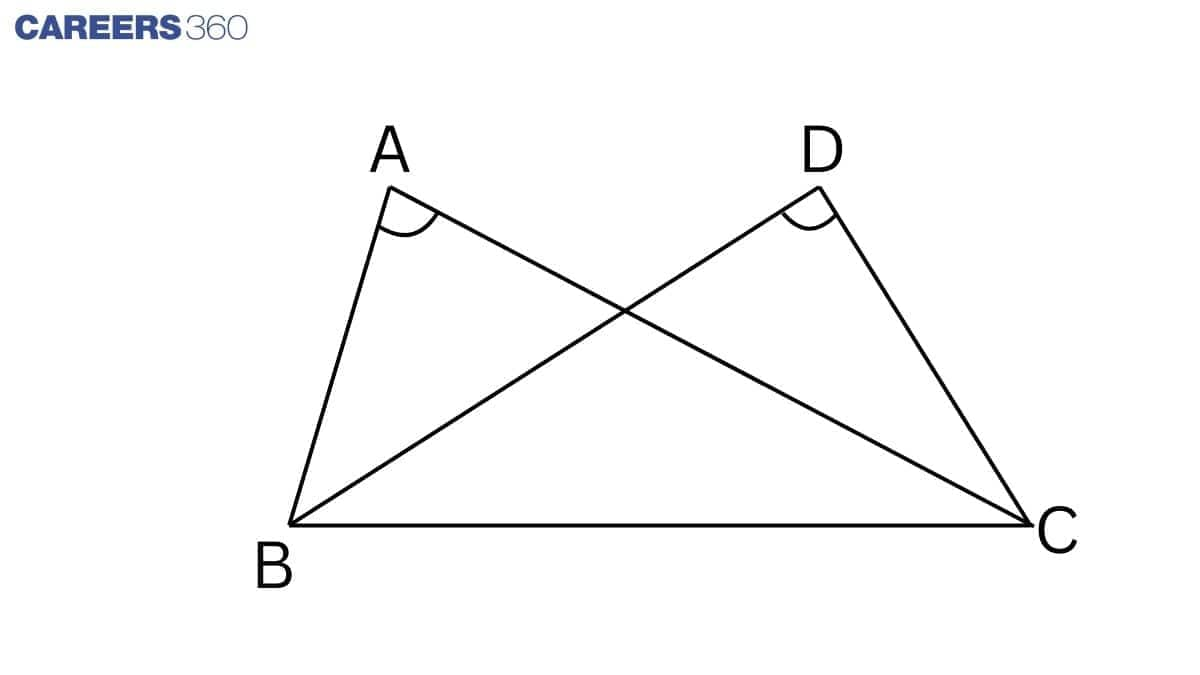
Triangle ABC and ADC are on a common base BC and $\angle$ BAC = $\angle$ BDC.
Thus, points A, B, C, and D lie in the same circle.
(If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, then four points lie on the circle.)
$\angle$ CAD = $\angle$ CBD (Angles in the same segment are equal)
Question 12: Prove that a cyclic parallelogram is a rectangle.
Answer:
Given: ABCD is a cyclic quadrilateral.
To prove: ABCD is a rectangle.
Proof:
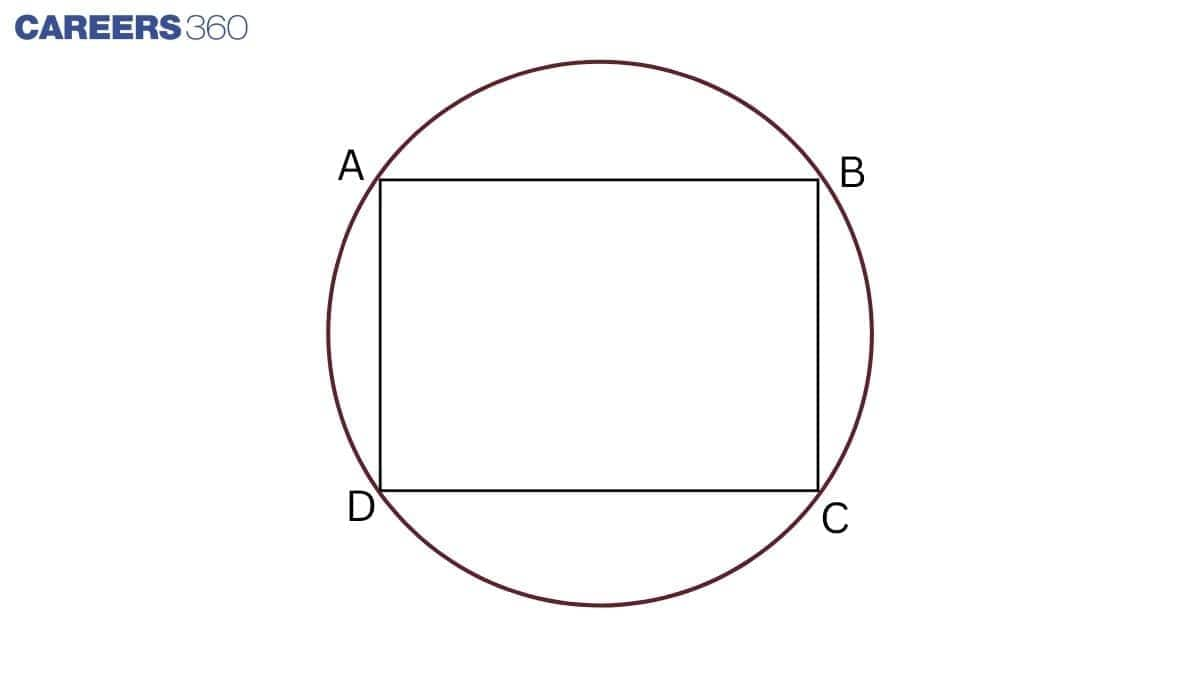
In cyclic quadrilateral ABCD.
$\angle A + \angle C = 180 ^\circ$ .......................1(sum of either pair of opposite angles of a cyclic quadrilateral)
$\angle A = \angle C$ ........................................2(opposite angles of a parallelogram are equal )
From 1 and 2,
$\angle A + \angle A = 180 ^\circ$
$\Rightarrow 2\angle A = 180 ^\circ$
$\Rightarrow \angle A = 90 ^\circ$
We know that a parallelogram with one angle a right angle is a rectangle.
Hence, ABCD is a rectangle.
Circles Class 9 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Circles Class 9 Maths Chapter 9 are provided in the links below.
Class 9 Maths NCERT Chapter 9: Extra Question
Question: The radius of a circle is 5 cm, and the length of the chord is 6 cm. Find the distance from the centre to its chord.
Answer:
Let AB = 6 cm be the chord of the circle with radius AO = 5 cm. Draw OP perpendicular to AB.
Now, apply Pythagoras' theorem
(AO)2 = (OP)2 + (AP)2
Here, AP = $\frac{1}{2}$ AB
So, AP = 3 cm
Now, putting values, we get:
52 = (OP)2 + 32
25 = (OP)2 + 9
(OP)2 = 16
Therefore, OP = 4 cm
Thus, the distance from the centre to its chord is 4 cm.
Circles Class 9 Chapter 9: Topics
Topics you will learn in NCERT Class 9 Maths Chapter 9 Circles include:
- Angle Subtended by a Chord at a Point
- Perpendicular from the Centre to a Chord
- Equal Chords and Their Distances from the Centre
- Angle Subtended by an Arc of a Circle
- Cyclic Quadrilaterals
Circles Class 9 Solutions - Important Formulae And Points
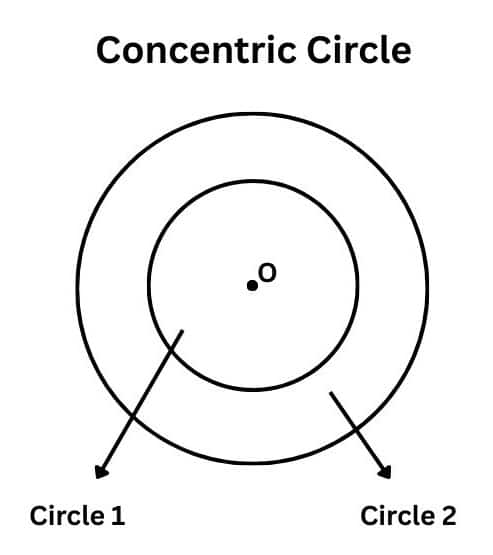
Concentric Circles: Concentric circles are circles that share the same centre but have different radii.
Arc: An arc of a circle is a continuous portion of the circle.
Chord of a Circle: The chord of a circle is a line segment that connects any two points on the circle.
Some Important Properties Of Circle Chords:
-
The diameter of a circle is a chord that passes through its centre.
-
A circle's diameter divides it into two equal arcs, forming a semicircle.
-
Congruent arcs have the same degree measure.
-
Equal arcs have associated chords of the same length.
-
A perpendicular drawn from the centre to a chord bisects the chord, and vice versa.
-
Three non-collinear points define one and only one circle.
-
Chords equidistant from the centre are equal in length.
-
The line connecting the centres of two intersecting circles and their common chord is perpendicular.
-
The central angle of an arc is twice the angle it subtends on the circumference.
-
Any two angles in the same circle segment are equal.
-
Equal chords of a circle create equal central angles at the centre.
-
The larger chord of a circle is closer to the centre than the smaller chord.
-
A semicircle contains a right angle.
-
Equal chords in a circle subtend equal angles at the centre.
Cyclic Quadrilateral
A four-sided polygon whose all four vertices lie on the circumference of a single circle is called a Cyclic quadrilateral.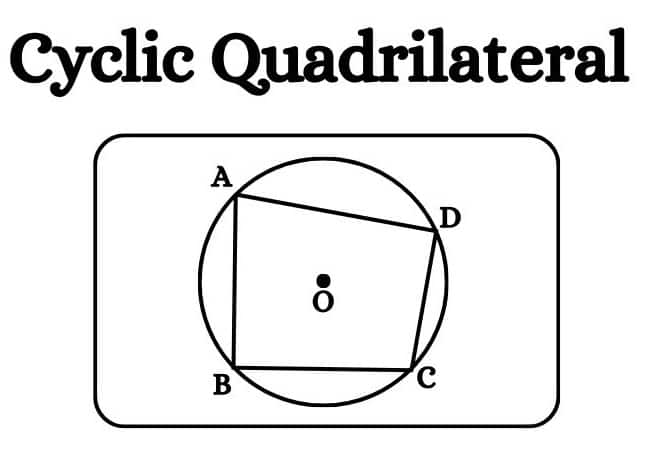
Condition of a Quadrilateral to be a Cyclic Quadrilateral
There are several conditions for a quadrilateral to be cyclic. Those are:
-
The sum of each pair of opposite angles must be 180 degrees. These angles are supplementary.
This is the most fundamental condition to be a cyclic quadrilateral.
-
All four vertices of the quadrilateral must touch the circumference of a single circle.
-
In cyclic quadrilaterals, the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals.
-
The perpendicular bisectors of a cyclic quadrilateral are always concurrent.
Tangent and Radius:
-
The tangent and radius of a circle intersect at a right angle.
Approach to Solve Questions of Circles Class 9
Using these approaches, students can tackle the Circles Class 9 Chapter 9 Question Answers with greater confidence.
- Learn key circle terms: Students must learn fundamental circle vocabulary that includes radius, diameter, chord, arc and tangent. These form the base of all problems in this chapter.
- Apply the perpendicular theorem: The perpendicular line drawn from the circle centre splits any chord exactly in two parts, and this property serves as a fundamental concept in many of our questions.
- Use equal chord concepts: An object which reaches the centre of a circle at the same distance from the centre holds an equal length to the object. The concepts apply to both numerical tasks and proof-based assignments.
- Understand angle subtended properties: Resolving angle problems requires knowing that the centre-point arc angle equals twice the angle derived at any circle-perimeter location.
- Practice cyclic quadrilateral concepts: Students should employ opposite angles of cyclic quadrilaterals, adding 180 degrees as a frequently examined concept.
- Draw neat diagrams and use logical steps: The ability to perform geometrical reasoning improves through diagrams which are correctly drawn, together with points clearly labelled, particularly when solving proof-based problems.
Why are Class 9 Maths Chapter 9 Circles Question Answers Important?
Circles are an important part of geometry that appear in many real-life situations. This chapter teaches how chords, arcs, and angles in a circle work together, helping us solve different problems easily and accurately. These Class 9 Maths Chapter 9 Circles question answers make it easier for students to practise and understand these concepts. Here are some more points on why these question answers are important:
- These solutions help you learn how angles and chords behave in a circle.
- These question answers make it easier to solve problems involving perpendiculars, arcs, and cyclic quadrilaterals.
- These Class 9 Maths Chapter 9 Circles question answers prepare you for higher classes where you’ll study advanced geometry and coordinate geometry involving circles.
NCERT Solutions For Class 9 Maths Chapter Wise
We at Careers360 compiled all the NCERT class 9 Maths solutions in one place for easy student reference. The following links will allow you to access them.
Also, read,
NCERT Books and NCERT Syllabus
Given below are some useful links for NCERT books and the NCERT syllabus for class 9:
Frequently Asked Questions (FAQs)
The perpendicular bisects the chord, dividing it into two equal parts.
A quadrilateral whose all vertices lie on a circle is called a cyclic quadrilateral.
At the centre, the angle formed by lines joining the ends of the arc to the centre
At the circumference, the angle formed by lines joining the ends of the arc to any point on the circle
Yes. Since exam questions are largely theorem-based, NCERT solutions are sufficient. Practising all examples and exercises ensures full preparation. Also, these solutions, created by Careers360 experts, are precise and comprehensive, making it easier for students to solve complex problems with greater efficiency. By mastering these solutions, students can establish a strong foundation in Geometry and achieve excellent scores in their final exams.
This chapter on NCERT Circles Class 9 solutions includes the following topics:
- Angle Subtended by a Chord at a Point
- Perpendicular from the Centre to a Chord
- Equal Chords and Their Distances from the Centre
- Angle Subtended by an Arc of a Circle
- Cyclic Quadrilaterals
Free downloadable PDFs are available on various reliable educational sites such as Careers360. You can also find a downloadable PDF of the solutions to this chapter from this article, as well as on the official page of Careers360.
Yes, there are many examples, including:
Wheels, coins, and round objects.
Circular plots or fields
Architecture and design
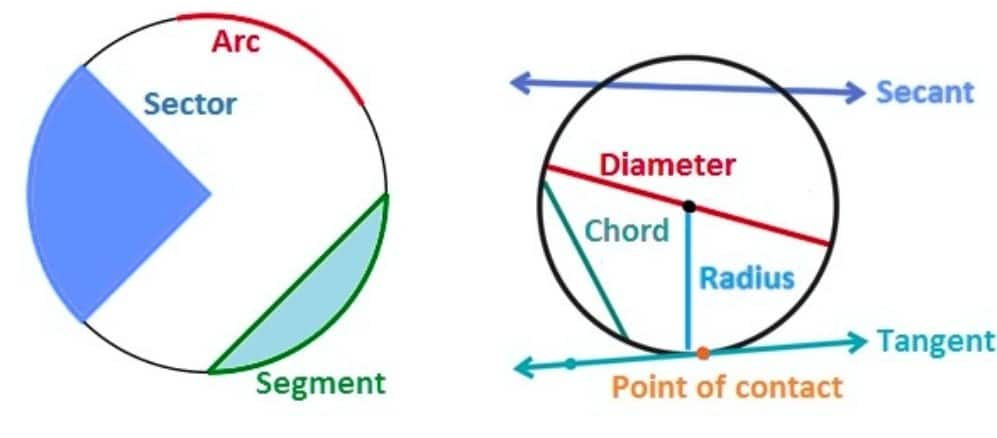
Chord: A line segment joining two points on the circle.
Secant: A line intersecting the circle at two points.
Tangent: A line touching the circle at one point only.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
