NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.1

Team Careers360Updated on 03 May 2025, 03:14 PM IST

A circle is a two-dimensional geometrical figure in which all points on the surface of the circle are equidistant from the centre point. A circle can be characterised as a shut (closed), two-dimensional curved shape, with no pointed vertex, with zero corners, such that every point of the circle is equidistant from the fixed centre of the circle. Radius is the distance from the centre of the circle to any point on the circumference of the circle. A circle's chord is the line segment that connects two locations on its circumference. The circumference of a circle is the perimeter of a circle; we can divide the circumference into two parts: a major arc and a minor arc. The major arc includes the majority portion of the arc, and the minor arc includes the minority portion of the arc. You will see that the angles subtended by two or more equal chords of a circle at the centre are equal if you draw two or more equal chords of a circle and determine the angles they occupy in the centre.

This Story also Contains

NCERT Solutions Class 9 Maths Chapter 1: Exercise 9.1
Topics Covered in Chapter 9, Circles: Exercise 9.1
NCERT Solutions of Class 9 Subject Wise
Subject-Wise NCERT Exemplar Solutions

Students can also get all NCERT solutions according to the standard and subjects. In Class 9 Maths chapter 9 exercise 9.1, we will cover the theorems of the angle subtended by a chord at a point in depth. The following exercises are also included in the NCERT Book Class 9 Mathematics chapter 9 exercise 9.1. Class 9 Maths chapter 9 exercise 9.1 is about the angle subtended by a chord at a point.

NCERT Solutions Class 9 Maths Chapter 1: Exercise 9.1

Q1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.

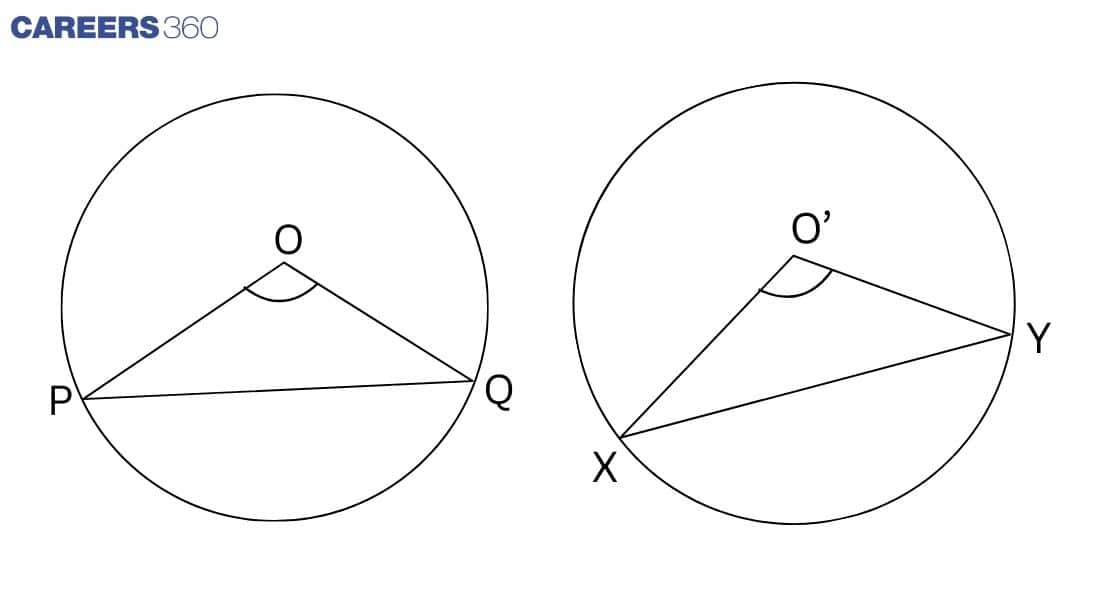
1745317842320

In the given figure, two congruent circles are given and have centers O and O', and chords are PQ and XY, respectively.
In Δ POQ and XO'Y
PQ = XY (Given)
OP = O'X (Radius of congruent triangle)
OQ = O'Y (Radius of congruent triangle)
ΔPOQ ≅ ΔXO'Y (By SSS rule)
Therefore, ∠POQ = ∠XO'Y (By CPCT)

Q2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Solution:
Given: Two congruent circles have equal angles.
To Prove: Two congruent circles have equal angles, and then the chords are equal.

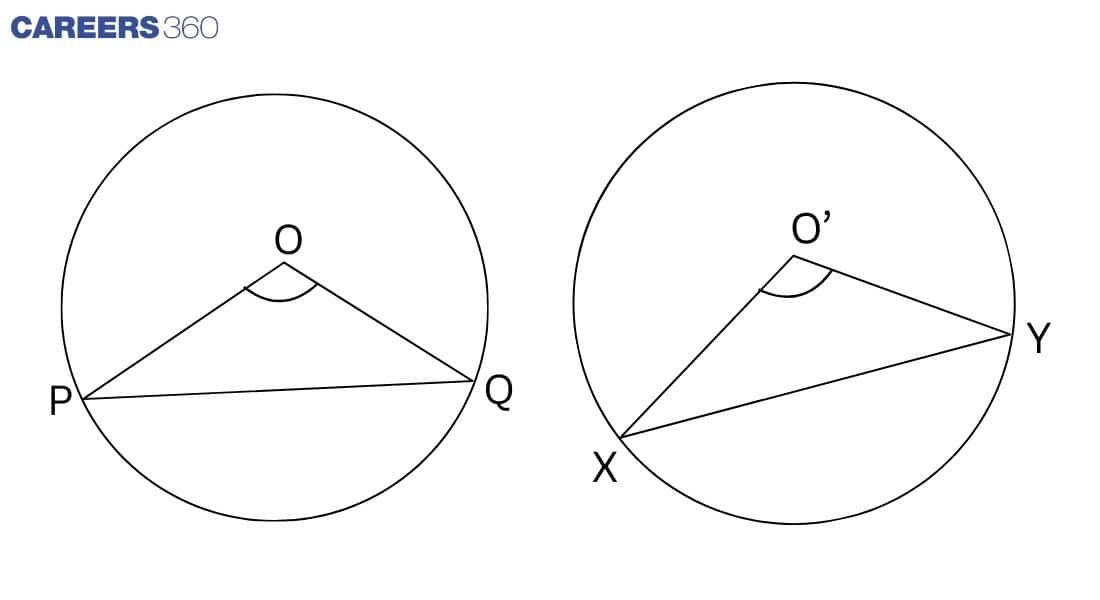
1745317875792

In Δ POQ and XO'Y
∠POQ = ∠XO'Y (Given)
OP = O'X (Radius of congruent triangle)
OQ = O'Y (Radius of congruent triangle)
ΔPOQ ≅ ΔXO'Y (By SSS rule)
Therefore, PQ = XY (By CPCT)

Also Read

Topics Covered in Chapter 9, Circles: Exercise 9.1

As we know NCERT solutions for exercise 9.1 Class 9 Maths chapter 9 are about the angle subtended by a chord at a point. But along with the topics about circles, such as chords, arc, major arc, minor arc, semicircle, we have also used the information about the congruence of the triangle, which we have covered in Class 9 Chapter 7 triangle. Some of the rules and properties which we are using are the side-side-side rule, the side-angle-side rule, and there are some theorems which are covered before Class 9 Maths chapter 9 exercise 9.1. These theorems are at the centre of a circle, equal chords subtend equal angles. If the angles subtended by the chords of a circle at its centre are equal, then the chords are equal, as well as the theorem.

Also See

NCERT Solutions of Class 9 Subject Wise

Students must check the NCERT solutions for Class 9 Maths and Science given below:

Subject-Wise NCERT Exemplar Solutions

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

Frequently Asked Questions (FAQs)

Q: What is the core concept of NCERT solutions for Class 9 Maths exercise 10.1?

This exercise deals with all the difficult questions regarding circles and its properties.

Q: Define a circle.

A circle can be defined as a closed, two-dimensional curved shape, with zero corners such that every point of the circle is equidistant from the fixed centre of the circle.

Q: What is the radius of a circle?

The radius of a circle is the straight line extending from the centre of a circle to the circumference or surface.

Q: What is the relation between radius and diameter of a circle?

diameter=2 radius

Q: Find the diameter of the circle if the radius is 10 cm?

The relation between the radius and diameter of a circle is:

diameter=2 radius

diameter=20 cm

Q: Which segment contains the centre of the circle?

The major segment of the circle contains the centre of the circle whereas the minor segment doesn’t include the centre.

Articles

DU BA LLB Eligibility Criteria 2026 - Age Limit, Qualifications, Marks

Sep 22, 2025

DU LLB Counselling 2026 – Seat Allotment, Documents, Admission Process

Sep 21, 2025

CGPA Calculator - Know How to Calculate CGPA

Sep 19, 2025

SOF IHO Exam 2026 – Dates, Registration, Syllabus & Pattern

Sep 19, 2025

Upcoming School Exams

National Means Cum-Merit Scholarship

Ongoing Dates

NMMS Application Date

25 Jul'25 - 30 Sep'25 (Online)

Uttar Pradesh Board 12th Examination

Ongoing Dates

UP Board 12th Others

10 Aug'25 - 27 Sep'25 (Online)

Mock Test

Exam Pattern

Result

Uttar Pradesh Board 10th examination

Ongoing Dates

UP Board 10th Others

10 Aug'25 - 27 Sep'25 (Online)

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is