What is the main concept of NCERT solutions for Class 9 Maths exercise 10.3?

In this exercise, we learn about perpendicular chords that the perpendicular from a circle's centre to a chord cuts the chord in half.

What is the perpendicular distance of the chord from the centre if the length of the chord is 8cm and the radius of the circle is 5cm?

The perpendicular distance is 3cm because the perpendicular from a circle's centre to a chord cuts the chord in half. So, the length of hypotenuse i.e. radius is 5cm, length of the base is 4cm hence by the Pythagoras theorem the length of perpendicular is 3cm.

A tangent is a line that intersects a circle in exactly one spot.

What is the angle between the radius and the point at which the tangent touches the circle?

The measure of the angle is 90 degrees.

What is the maximum number a line can meet a circle?

A line can meet a maximum of two times a circle.

NCERT Solutions for Exercise 10.3 Class 9 Maths Chapter 10

Team Careers360Updated on 29 Jul 2022, 06:34 PM IST

NCERT Solutions for Class 9 Maths exercise 10.3 - We will first look at the basics definition of the circle then go through the theorems discussed in Class 9 Maths chapter 10 exercise 10.3. A circle is any closed shape with all points connected at an equal distance from the centre. The centre of the circle is any point that is equidistant from any of the circle's boundaries. Radius is a Latin word that means 'ray,' but it refers to the line segment that runs from the circle's centre to its edge. The radius of a circle is defined as any line that starts or ends at the centre of the circle and connects to any point on the circle's border.

This Story also Contains

Circles Class 9 Chapter 10 Circles Exercise: 10.3
More About NCERT Solutions for Class 9 Maths Exercise 10.3
Benefits of NCERT Solutions for Class 9 Maths Exercise 10.3
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions

NCERT solutions Class 9 Maths exercise 10.3 – This exercise includes some important theorems for examination point of view which are related to chords. We will first see the definition of a chord.

Chord:

Any straight-line segment with both endpoints on the circle's boundary is called a Chord. It literally means 'bowstring' in Latin.

The theorems are:

The perpendicular from a circle's centre to a chord cuts the chord in half.

The line that bisects a chord through the centre of a circle is perpendicular to the chord.

There is only one circle that passes through all three non-collinear points. Circumcircle is the name given to this circle. The Circumcentre and Circumradius are their centre and radius, respectively.

Along with Class 9 Maths ch 9 exercise, 10.3 the following exercises are also present.

Circles Class 9 Chapter 10 Circles Exercise: 10.3

Q1 Draw different pairs of circles. How many points does each pair have in common? What ii the maximum number of common points?

Answer:

1640237144301

In (i) we do not have any common point.

In (ii) we have 1 common point.

In (iii) we have 1 common point.

In (iv) we have 2 common points.

The maximum number of common points is 2.

Q2 Suppose you are given a circle. Give a construction to find its centre.
Answer:

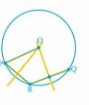
1640237176161

Given : Points P,Q,R lies on circle.

Construction :

1. Join PR and QR

2. Draw perpendicular bisector of PR and QR which intersects at point O.

3. Taking O as centre and OP as radius draw a circle.

4. The circle obtained is required.

Q3 If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

Answer:

Given: Two circles intersect at two points.

To prove: their centres lie on the perpendicular bisector of the common chord.

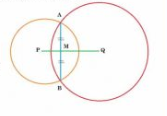
1640237204682

Construction: Joinpoint P and Q to midpoint M of chord AB.

Proof: AB is a chord of circle C(Q,r) and QM is the bisector of chord AB.

$\therefore PM\perp AB$

Hence, $\angle PMA =90 ^\circ$

Similarly, AB is a chord of circle(Q,r' ) and QM is the bisector of chord AB.

$\therefore QM\perp AB$

Hence, $\angle QMA =90 ^\circ$

Now, $\angle QMA +\angle PMA=90 ^\circ+90 ^\circ= 180 ^\circ$

$\angle$ PMA and $\angle$ QMA are forming linear pairs so PMQ is a straight line.

Hence, P and Q lie on the perpendicular bisector of common chord AB.

Benefits of NCERT Solutions for Class 9 Maths Exercise 10.3

NCERT book Exercise 10.3 Class 9 Maths, is related to the circle and chords.
NCERT syllabus Class 9 Maths chapter 10 exercise 10.3 introduces us to theorems related to the chords in a circle.
Understanding the concepts from Class 9 Maths chapter 10 exercise 10.3 will allow us to understand the concepts related to the theorems of chords and circles.

Also, See

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Articles

IOQM Admit Card 2025: Download Indian Olympiad Qualifier in Mathematics Hall Ticket

Aug 29, 2025

Cambridge IGCSE Result 2025: Check Cambridge IGCSE Result Dates & Grading System

Aug 26, 2025

Anuprati Coaching Yojana 2025-26 : Scheme Dates, How to Apply, Benefits, Selection Process

Aug 26, 2025

Anuprati Coaching Yojana Eligibility Criteria 2025-26 : Categories: SC, ST, OBC, MBC, and EWS

Aug 26, 2025

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is