NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry

Have you ever wondered how different locations are marked and plotted in Google Maps? Or have you wondered how building plans are plotted in the exact correct shape? Coordinate Geometry plays a key role in all of this. Coordinate Geometry is all about the representation of points in the graph with the x-axis and y-axis. The chapter on Coordinate Geometry is an important fundamental topic of all higher-level Geometric topics. This article contains NCERT Solutions for Class 9, which are designed by Subject Matter Experts in Careers360, making it a reliable study resource. These NCERT solutions are very helpful resources for students to practice the exercise problems and check their answers.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

This Story also Contains

1. Coordinate Geometry Class 9 Questions And Answers PDF Free Download
2. Coordinate Geometry Class 9 Solutions - Important Formulae
3. Coordinate Geometry Class 9 NCERT Solutions (Exercise)
4. NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry - Points to Remember
5. NCERT Solutions for Class 9 Maths Chapter Wise
6. NCERT Solutions for Class 9 Subject-wise
7. NCERT Class 9 Other Resources

Additionally, students can refer to Coordinate Geometry Class 9 NCERT Chapter 3 Notes to understand the concepts covered in this chapter. These notes simplify and provide the important concepts and formulas that would help to revise during the exam preparation.

Coordinate Geometry Class 9 Questions And Answers PDF Free Download

Download PDF

Coordinate Geometry Class 9 Solutions - Important Formulae

Axis:

The Cartesian plane is divided by two perpendicular lines called axes (Singular: Axis). The horizontal line is called the x-axis, and the vertical line is called the y-axis.

Origin:

The intersection of the two lines at (0,0) is called the Origin.

Coordinate:

Any point marked on the Cartesian plane is called a coordinate. The coordinate is represented as (x,y). Eg. (1,2)

The coordinate of the Origin is (0,0).

Quadrants:

The x-axis and y-axis divide the Cartesian plane into 4 sections called Quadrants.

The signs of coordinates in each quadrant are,

First quadrant: (+, +)

Second quadrant: (–, +)

Third quadrant: (–, –)

Fourth quadrant: (+, –)

Coordinate Geometry Class 9 NCERT Solutions (Exercise)

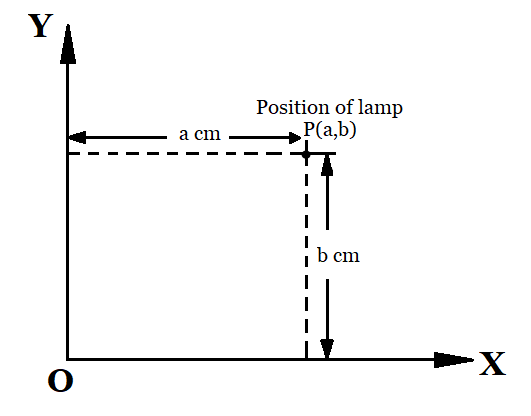
Q1 How would you describe the position of a table lamp on your study table to another person?

Answer:

To describe the position of a table lamp placed on the table,

Let us consider the table lamp as P and the table as a plane.

Then, we consider two perpendicular edges of the table as the axes OX and OY.

From OY, measure the perpendicular distance ${}^{\prime }{a}^{\prime }cm$ of P.

From OX, measure the perpendicular distance ${}^{\prime }{b}^{\prime }cm$ of P.

Thus, the position of the lamp is then given by;

Q2 (i) (Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city in your notebook. Represent the roads/streets by single lines.

There are many cross-streets in your model. A particular cross-street is made of two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North-South direction and 5th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find how many cross-streets can be referred to as (4, 3).

Answer:

(i) From the figure:

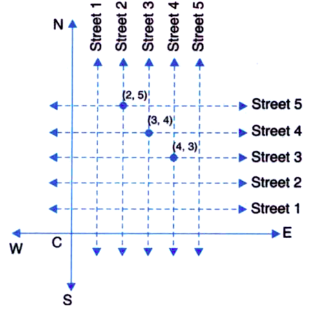
There is only one cross - streets which can be referred to as (4, 3).

Q2 (ii) (Street Plan): A city has two main roads that cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city in your notebook. Represent the roads/streets by single lines.

There are many cross-streets in your model. A particular cross-street is made of two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North-South direction and 5th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find how many cross-streets can be referred to as (3, 4).

Answer:

(ii) From the figure:

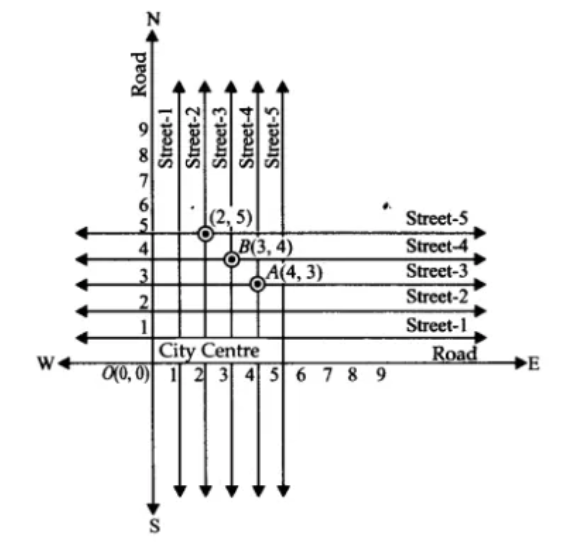
The cross street is shown by the point $B(3,4).$

We have located the two cross streets because of the two reference lines.

Q1 (i) Write the answer to each of the following questions:

What are the names of the horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?

Answer:

The Horizontal line is the x-axis, and the Vertical line is the y-axis.

Q1 (ii) Write the answer to each of the following questions:

What is the name of each part of the plane formed by these two lines?

Answer:

The name of each part of the plane formed by the x-axis and the y-axis is called "Quadrant".

Q1 (iii) Write the answer to each of the following questions:

Write the name of the point where these two lines intersect.

Answer:

The point where the x-axis and y-axis both intersect is known as the Origin.

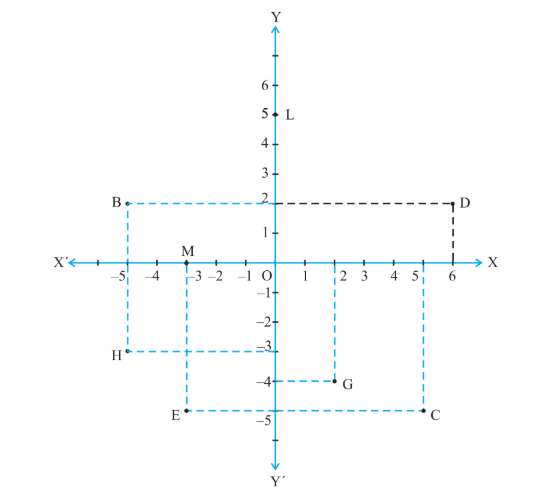
Q2 See Fig.3.14, and write the following:

(i) The coordinates of B.

(ii) The coordinates of C.

(iii) The point identified by the coordinates (–3, –5).

(iv) The point identified by the coordinates (2, – 4).

(v) The abscissa of the point D.

(vi) The ordinate of the point H.

(vii) The coordinates of the point L.

(viii) The coordinates of the point M.

Answer:

From the figure:

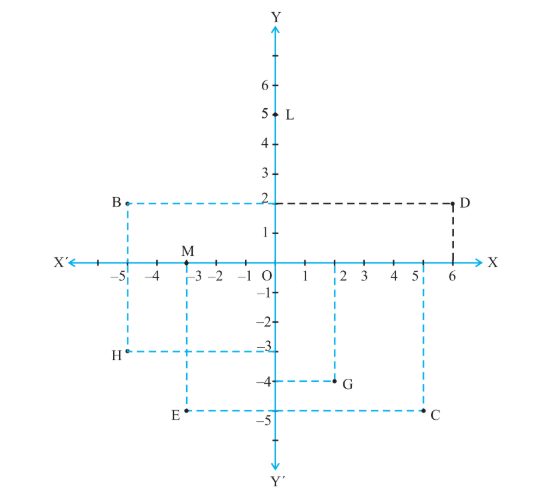
(i) The coordinates of B are $(-5,2).$

(ii) The coordinates of C are $(5,-5).$

(iii) Point E is identified by the coordinates (–3, –5).

(iv) Point G is identified by the coordinates (2, – 4).

(v) The abscissa of point D is 6.

(vi) The ordinate of the point H is -3.

(vii) The coordinates of the point L are $(0,5).$

(viii) The coordinates of the point M are $(-3,0).$

Interested students can also check the exercise-wise solutions of class 9 Maths chapter 3.

• Coordinate Geometry Exercise 3.1
• Coordinate Geometry Exercise 3.2

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry - Points to Remember

The important points to remember in Coordinate Geometry are,

• To plot a point on a plane, we need two perpendicular lines called the x-axis(horizontal line) and the y-axis(vertical line)
• These axes are called coordinate axes
• The point at which the axes intersect is called the origin, which is (0,0)
• The x-coordinate is the distance from the y-axis, and the y-coordinate is the distance from the x-axis
• The points on the x-axis are in the form (x,0,) and the points on the y-axis are in the form (0,y)
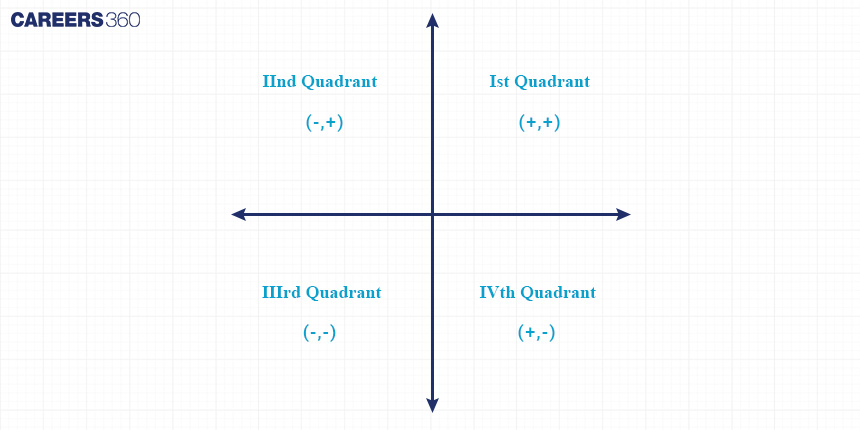
• The coordinate axes divide the cartesian plane into four parts called the quadrants. The coordinates in each quadrant differ from the signs of the coordinates
• First quadrant: (+, +)
  Second quadrant: (–, +)
  Third quadrant: (–, –)
  Fourth quadrant: (+, –)

NCERT Solutions for Class 9 Maths Chapter Wise

NCERT Solutions for Class 9 Subject-wise

We at Careers360 also provide solutions for other class 9 subjects. These subject-wise solutions contain the solutions for all the chapters of Class 9 subject-wise. Below are the subject-wise Class 9 solutions.

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

Additionally, to practice extra questions in NCERT Exemplar and analyse their performance using NCERT Exemplar Solutions for Class 9 Maths Chapter 3 Coordinate Geometry.

NCERT Class 9 Other Resources

Students can also refer to NCERT Books and Syllabus for Class 9 provided by Careers360 using the below-mentioned links.

• NCERT Books Class 9 Maths
• NCERT Syllabus Class 9 Maths
• NCERT Books Class 9
• NCERT Syllabus Class 9