NCERT Solutions for Class 9 Maths Chapter 3 Exercise 3.1

Vishal kumarUpdated on 20 May 2025, 02:31 PM IST

Coordinate geometry uses one or more numbers or coordinates to determine the position of points or other geometric elements in the Cartesian plane. It is an important concept that uses graphs and curves to provide links between geometry and algebra. To describe the position of a point in a plane Cartesian system is used. In this Cartesian system, one horizontal and one vertical line are used, and the point where these two lines intersect is called the origin, and it is denoted by $O$.

This Story also Contains

NCERT Solutions for Class 9 Maths Chapter 3- Coordinate Geometry Exercise 3.1
Access Coordinate Geometry Class 9 Chapter 3 Exercise 3.1
Topics covered in Chapter 3 Coordinate Geometry: Exercise 3.1
NCERT Solutions of Class 9 Subject Wise
Subject-Wise NCERT Exemplar Solutions

NCERT Solutions for Class 9 Maths Chapter 3 Exercise 3.1 - Coordinate Geometry

In exercise 3.1 Class 9 Maths, we have given an idea about how to write the coordinates of a location, how to find the coordinates, how it is applied and when we can use it in real life. In the NCERT solutions for Class 9 Maths exercise 3.1, the focus is on how to apply coordinate geometry in real-life applications and gives us the essence of the importance of this branch of mathematics. These solutions provided for exercise 3.1 class 9 maths are created by subject experts at Careers360, ensuring a detailed and easily understandable explanation. This exercise typically consists of two questions, each with various parts. Additionally, the class 9 maths chapter 3 exercise 3.1 is accessible in PDF format, allowing students to use it offline at their convenience, free of cost. Apart from NCERT solutions, the NCERT Books serve as a valuable resource to aid in understanding and mastering the mathematical concepts presented in this exercise.

NCERT Solutions for Class 9 Maths Chapter 3- Coordinate Geometry Exercise 3.1

Access Coordinate Geometry Class 9 Chapter 3 Exercise 3.1

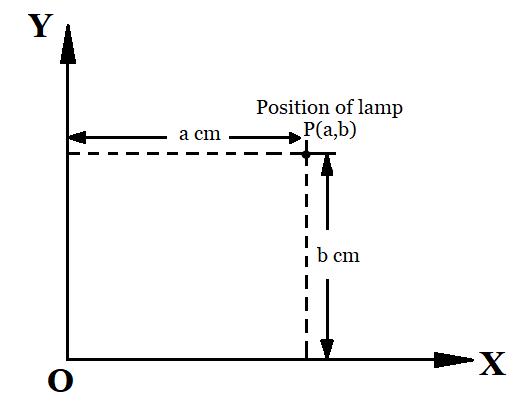
Q1 How will you describe the position of a table lamp on your study table to another person?

Answer:

To describe the position of a table lamp placed on the table,

Let us consider the table lamp as P and the table as a plane.

Then, we consider two perpendicular edges of the table as the axes OX and OY.

From OY measure the perpendicular distance $'a'\ cm$ of P.

From OX measure the perpendicular distance $'b'\ cm$ of P.

Thus, the position of the lamp is then given by;

1640063724882

Q2 (i) (Street Plan) : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2 nd street running in the North-South direction and 5 th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find: how many cross - streets can be referred to as (4, 3).

Answer:

(i) From the figure:

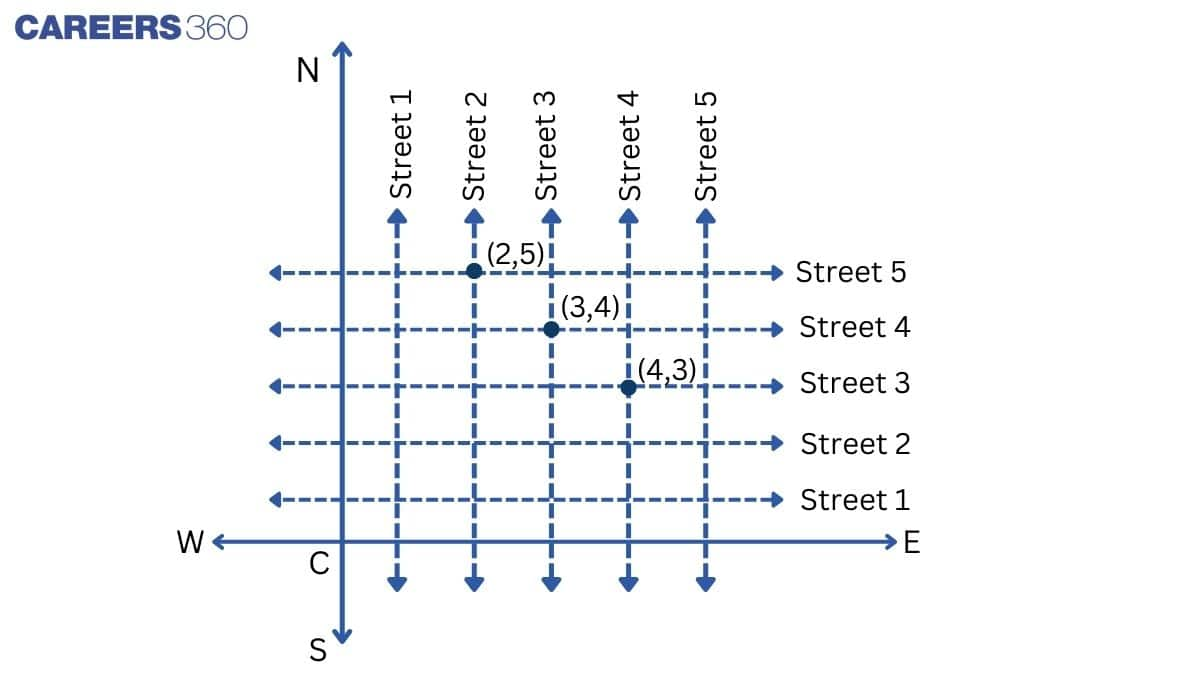
1745306997410

There is only one cross-street which can be referred to as (4, 3).

Q2 (ii) (Street Plan) : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.

There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2 nd street running in the North-South direction and 5 th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find: how many cross - streets can be referred to as (3, 4).

Answer:

(ii) From the figure:

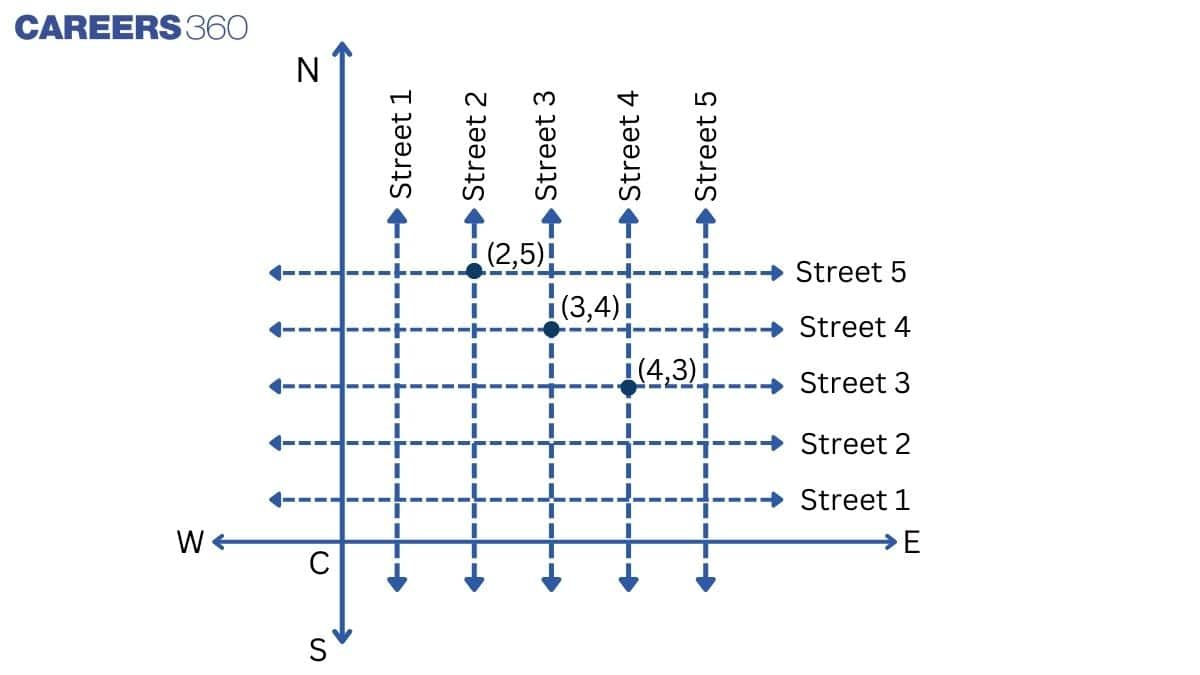
1745307039406

The cross street is shown by the point $B(3,4).$
We have located the one cross street.

Also Read:

Coordinate Geometry Exercise 3.2

Topics covered in Chapter 3 Coordinate Geometry: Exercise 3.1

1. Definition of coordinate geometry, Cartesian system, origin, quadrants, Abscissa, Ordinate, Collinear Points.
2. Distance Formula to determine the distance between two points.
3. Midpoint Formula to find the midpoints of the coordinates.
4. Section Formula, to find the coordinates that divide the line segment into a given ratio.

Also See

NCERT Solutions of Class 9 Subject Wise

Students must check the NCERT solutions for Class 9 Maths and Science given below:

Subject-Wise NCERT Exemplar Solutions

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

Frequently Asked Questions (FAQs)

Q: Examples of coordinates in real life and what would be the world without them?

Coordinates are used throughout the world for various purposes such as in scientific inventions, world maps to find the location as well as in construction and there are many more examples without coordinate we cannot grow a civilization

Q: In the NCERT solutions for Class 9 Maths chapter 3 exercise, how many questions are covered?

In Class 9 Mathematics chapter exercise 3.1, there are two problems.

Q: What sorts of questions are included in the NCERT solutions for chapter 3 of Maths for Class 9?

Both questions are about the real-life application of coordinates question is creating a simulation of lamp and we have to move it in the second question has two subparts and it is about arrangements of road

Q: What is coordinate geometry according to NCERT solutions for Class 9 Maths exercise 3.1?

The study of geometry using the coordinate points is known as coordinate geometry

Q: What is coordinates according to NCERT solutions for Class 9 Maths exercise 3.1?

Are a way to find the location of any object on two dimensional or three-dimensional plane

Q: How many activities are covered before exercise 3.1 Class 9 Maths and what it is about?

There is one activity covered before exercise 3.1 Class 9 Maths which is about the seating arrangement of seats of students

Q: Who developed the idea of the cartesian system as covered before NCERT solutions for Class 9 Maths exercise 3.1?

René Déscartes. Developed the cartesian system

Q: Explain in brief about the developer of the cartesian system.

René Déscartes is the great French mathematician of the seventeenth century and he developed the cartesian system.

Articles

IOQM Answer Key 2025: Download IOQM Solution PDF for All Sets

Sep 02, 2025

SOF IEO Sample Papers 2025-26 For Classes 1 to 12 (Free PDF)

Sep 02, 2025

IOQM Admit Card 2025: Download Indian Olympiad Qualifier in Mathematics Hall Ticket

Aug 29, 2025

Cambridge IGCSE Result 2025: Check Cambridge IGCSE Result Dates & Grading System

Aug 26, 2025

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is