NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

Edited By Ramraj Saini | Updated on Oct 06, 2023 08:15 AM IST

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

Polynomials Class 9 Questions And Answers are provided here. A polynomial is an algebraic expression which consists of variables and coefficient with operations such as additions, subtraction, multiplication, and non-negative exponents. In this particular NCERT syllabus Class 9 chapter, you will learn the operations of two or more polynomials. NCERT solutions which are prepared by subjects expert at Careers360 keeping in mind of latest CBSE syllabus 2023, are there to help you while solving the problems related to this NCERT book Class 9 Maths chapter. Polynomials Class 9, introduces a lot of important concepts that will be helpful for those students who are targeting exams like JEE, CAT, SSC, etc.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials
Polynomials Class 9 Questions And Answers PDF Free Download
Polynomials Class 9 Solutions - Important Formulae
Polynomials Class 9 NCERT Solutions (Intext Questions and Exercise)
More About NCERT Solutions For Class 9 Maths Chapter 2 Polynomials
NCERT Solutions for Class 9 Maths Chapter Wise
Key Features of NCERT Solutions For chapter 2 maths class 9
NCERT Solutions for Class 9 Subject Wise
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

This chapter talk about Polynomials in One Variable, Zeroes of a Polynomial, Remainder Theorem, Factorisation of Polynomials, and Algebraic Identities. NCERT solutions for Class 9 Maths chapter 2 Polynomials can also be used while doing homework. It can be a good tool for the Class 9 students as it is designed in such a manner so that a student can fetch the maximum marks available for the particular question. Here students will get NCERT solutions for Class 9 also.

Also Read|

Polynomials Class 9 Questions And Answers PDF Free Download

Download PDF

Polynomials Class 9 Solutions - Important Formulae

The general form of a polynomial is: p(x) = a_nxⁿ + a_n-1x^n-1 + … + a₂x² + a₁x + a₀

where a₀, a₁, a₂, …. an are constants, and a_n ≠ 0.

Every one-variable linear polynomial will contain a unique zero, which is a real number that is a zero of the zero polynomial, and a non-zero constant polynomial that does not have any zeros.

>> Remainder Theorem: If p(x) has a degree greater than or equal to 1, and you divide p(x) by the linear polynomial (x - a), the remainder will be p(a).

>> Factor Theorem: The linear polynomial (x - a) will be a factor of the polynomial p(x) whenever p(a) = 0. Similarly, if (x - a) is a factor of p(x), then p(a) = 0.

Free download NCERT Solutions for Class 9 Maths Chapter 2 Polynomials for CBSE Exam.

Polynomials Class 9 NCERT Solutions (Intext Questions and Exercise)

NCERT Polynomials class 9 solutions Exercise: 2.1

Q1 (i) Is the following expression polynomial in one variable? State reasons for your answer. $4x^2 - 3x + 7$

Answer:

YES
Given polynomial $4x^2 - 3x + 7$ has only one variable which is x

Q1 (ii) Is the following expression polynomial in one variable? State reasons for your answer. $y^2 + \sqrt2$

Answer:

YES
Given polynomial has only one variable which is y

Q1 (iii) Is the following expression polynomial in one variable? State reasons for your answer. $3\sqrt t + t\sqrt2$

Answer:

NO
Because we can observe that the exponent of variable t in term $3\sqrt t$ is $\frac{1}{2}$ which is not a whole number.
Therefore this expression is not a polynomial.

Q1 (iv) Is the following expression polynomial in one variable? State reasons for your answer. $y + \frac{2}{y}$

Answer:

NO
Because we can observe that the exponent of variable y in term $\frac{2}{y}$ is $-1$ which is not a whole number. Therefore this expression is not a polynomial.

Q1 (v) Is the following expression polynomial in one variable? State reasons for your answer. $x^{10} + y^3 + t^{50}$

Answer:

NO
Because in the given polynomial $x^{10} + y^3 + t^{50}$ there are 3 variables which are x, y, t. That's why this is polynomial in three variable not in one variable.

Q2 (i) Write the coefficients of $x^2$ in the following: $2 + x^2 +x$

Answer:

Coefficient of $x^2$ in polynomial $2 + x^2 +x$ is 1.

Q2 (ii) Write the coefficients of $x^2$ in the following: $2 - x^2 + x^3$

Answer:

Coefficient of $x^2$ in polynomial $2 - x^2 + x^3$ is -1.

Q2 (iii) Write the coefficients of $x^2$ in the following: $\frac{\pi}{2}x^2 + x$

Answer:

Coefficient of $x^2$ in polynomial $\frac{\pi}{2}x^2 + x$ is $\frac{\pi}{2}$

Q2 (iv) Write the coefficients of $x^2$ in the following: $\sqrt2 x - 1$

Answer:

Coefficient of $x^2$ in polynomial $\sqrt2 x - 1$ is 0

Q3 Give one example each of a binomial of degree 35, and of a monomial of degree 100.

Answer:

Degree of a polynomial is the highest power of the variable in the polynomial.
In binomial, there are two terms
Therefore, binomial of degree 35 is
Eg:- $x^{35}+1$
In monomial, there is only one term in it.
Therefore, monomial of degree 100 can be written as $y^{100}$

Q4 (i) Write the degree the following polynomial: $5x^3 + 4x^2 + 7x$

Answer:

Degree of a polynomial is the highest power of the variable in the polynomial.
Therefore, the degree of polynomial $5x^3 + 4x^2 + 7x$ is 3 .

Q4 (ii) Write the degree the following polynomial: $4 - y^2$

Answer:

Degree of a polynomial is the highest power of the variable in the polynomial.

Therefore, the degree of polynomial $4 - y^2$ is 2.

Q4 (iii) Write the degree the following polynomial: $5t - \sqrt7$

Answer:

Degree of a polynomial is the highest power of the variable in the polynomial.

Therefore, the degree of polynomial $5t - \sqrt7$ is 1

Q4 (iv) Write the degree the following polynomial: 3

Answer:

Degree of a polynomial is the highest power of the variable in the polynomial.

In this case, only a constant value 3 is there and the degree of a constant polynomial is always 0.

Q5 (i) Classify the following as linear, quadratic and cubic polynomial: $x^2+x$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $x^2+x$ with degree 2

Therefore, it is a quadratic polynomial.

Q5 (ii) Classify the following as linear, quadratic and cubic polynomial: $x - x^3$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $x - x^3$ with degree 3

Therefore, it is a cubic polynomial

Q5 (iii) Classify the following as linear, quadratic and cubic polynomial: $y + y^2 + 4$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $y + y^2 + 4$ with degree 2

Therefore, it is quadratic polynomial.

Q5 (iv) Classify the following as linear, quadratic and cubic polynomial: $1 +x$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $1 +x$ with degree 1

Therefore, it is linear polynomial

Q5 (v) Classify the following as linear, quadratic and cubic polynomial: $3t$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $3t$ with degree 1

Therefore, it is linear polynomial

Q5 (vi) Classify the following as linear, quadratic and cubic polynomial: $r^2$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $r^2$ with degree 2

Therefore, it is quadratic polynomial

Q5 (vii) Classify the following as linear, quadratic and cubic polynomial: $7x^3$

Answer:

Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively

Given polynomial is $7x^3$ with degree 3

Therefore, it is a cubic polynomial

Polynomials class 9 NCERT solutions Exercise: 2.2

Q1 (i) Find the value of the polynomial $5x - 4x^2 +3$ at $x = 0$

Answer:

Given polynomial is $5x - 4x^2 +3$

Now, at $x = 0$ value is

$\Rightarrow 5(0)-4(0)^2+3 = 0 - 0 + 3 = 3$

Therefore, value of polynomial $5x - 4x^2 +3$ at x = 0 is 3

Q1 (ii) Find the value of the polynomial $5x - 4x^2 +3$ at $x = -1$

Answer:

Given polynomial is $5x - 4x^2 +3$

Now, at $x = -1$ value is

$\Rightarrow 5(-1)-4(-1)^2+3 = -5 - 4 + 3 = -6$

Therefore, value of polynomial $5x - 4x^2 +3$ at x = -1 is -6

Q1 (iii) Find the value of the polynomial $5x - 4x^2 +3$ at $x = 2$

Answer:

Given polynomial is $5x - 4x^2 +3$

Now, at $x = 2$ value is

$\Rightarrow 5(2)-4(2)^2+3 = 10 - 16 + 3 = -3$

Therefore, value of polynomial $5x - 4x^2 +3$ at x = 2 is -3

Q2 (i) Find p(0) , p(1) and p(2) for each of the following polynomials: $p(y)= y^2 - y + 1$

Answer:

Given polynomial is

$p(y)= y^2 - y + 1$

Now,

$p(0)= (0)^2 - 0 + 1= 1$

$p(1)= (1)^2 - 1 + 1 = 1$

$p(2)= (2)^2 - 2 + 1 = 3$

Therefore, values of p(0) , p(1) and p(2) are 1 , 1 and 3 respectively .

Q2 (ii) Find p(0) , p(1) and p(2) for each of the following polynomials: $p(t) = 2 + t + 2t^2 - t^3$

Answer:

Given polynomial is

$p(t) = 2 + t + 2t^2 - t^3$

Now,

$p(0) = 2 + 0 + 2(0)^2 - (0)^3 = 2$

$p(1) = 2 + 1 + 2(1)^2 - (1)^3 = 4$

$p(2) = 2 + 2 + 2(2)^2 - (2)^3 = 4$

Therefore, values of p(0) , p(1) and p(2) are 2 , 4 and 4 respectively

Q2 (iii) Find p(0), p(1) and p(2) for each of the following polynomials: $p(x) = x^3$

Answer:

Given polynomial is

$p(x) = x^3$

Now,

$p(0) = (0)^3 =0$

$p(1) = (1)^3=1$

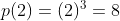
p(2) = (2)^3=8
Therefore, values of p(0) , p(1) and p(2) are 0 , 1 and 8 respectively

Q2 (iv) Find p(0), p(1) and p(2) for each of the following polynomials: $p(x)= (x-1)(x+ 1)$

Answer:

Given polynomial is

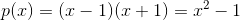
p(x)= (x-1)(x+ 1) = x^2-1
Now,

$p(0) = (0)^2-1 = -1$

$p(1) = (1)^2-1 = 0$

$p(2) = (2)^2-1 = 3$

Therefore, values of p(0) , p(1) and p(2) are -1 , 0 and 3 respectively

Q3 (i) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = 3x + 1, x = -\frac{1}{3}$

Answer:

Given polynomial is $p(x) = 3x + 1$

Now, at $x = -\frac{1}{3}$ it's value is

$p\left ( -\frac{1}{3} \right )=3\times \left ( -\frac{1}{3} \right )+1 = -1+1=0$

Therefore, yes $x = -\frac{1}{3}$ is a zero of polynomial $p(x) = 3x + 1$

Q3 (ii) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = 5x - \pi, x = \frac{4}{5}$

Answer:

Given polynomial is $p(x) = 5x - \pi$

Now, at $x =\frac{4}{5}$ it's value is

$p\left ( \frac{4}{5} \right )=5\times \left ( \frac{4}{5} \right ) -\pi = 4-\pi \neq 0$
Therefore, no $x =\frac{4}{5}$ is not a zero of polynomial $p(x) = 5x - \pi$

Q3 (iii) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = x^2 -1, x = 1,-1$

Answer:

Given polynomial is $p(x) = x^2-1$

Now, at x = 1 it's value is

$p(1) = (1)^2-1 = 1 -1 =0$

And at x = -1

$p(-1) = (-1)^2-1 = 1 -1 =0$
Therefore, yes x = 1 , -1 are zeros of polynomial $p(x) = x^2-1$

Q3 (iv) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = (x + 1)(x-2), x = -1,2$

Answer:

Given polynomial is $p(x) = (x+1)(x-2)$

Now, at x = 2 it's value is

$p(2) = (2+1)(2-2) = 0$

And at x = -1

$p(-1) = (-1+1)(-1-2) = 0$

Therefore, yes x = 2 , -1 are zeros of polynomial $p(x) = (x+1)(x-2)$

Q3 (v) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = x^2. x =0$

Answer:

Given polynomial is $p(x) = x^2$

Now, at x = 0 it's value is

$p(0) = (0)^2=0$

Therefore, yes x = 0 is a zeros of polynomial $p(x) = (x+1)(x-2)$

Q3 (vi) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = lx + m, \ x =- \frac{m}{l}$

Answer:

Given polynomial is $p(x) = lx+m$

Now, at $x = -\frac{m}{l}$ it's value is

$p\left ( -\frac{m}{l} \right )= l \times \left ( -\frac{m}{l} \right )+m = -m+m =0$

Therefore, yes $x = -\frac{m}{l}$ is a zeros of polynomial $p(x) = lx+m$

Q3 (vii) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = 3x^2 - 1, \ x = -\frac{1}{\sqrt3}, \frac{2}{\sqrt3}$

Answer:

Given polynomial is $p(x) = 3x^2-1$

Now, at $x = -\frac{1}{\sqrt3}$ it's value is

$p\left ( -\frac{1}{\sqrt3} \right )= 3 \times \left ( -\frac{1}{\sqrt3} \right )^2-1 = 1-1 =0$

And at $x = \frac{2}{\sqrt3}$

$p\left ( \frac{2}{\sqrt3} \right )= 3 \times \left ( \frac{2}{\sqrt3} \right )^2-1 = 4-1 =3\neq 0$

Therefore, $x = -\frac{1}{\sqrt3}$ is a zeros of polynomial $p(x) = 3x^2-1$ .

whereas $x = \frac{2}{\sqrt3}$ is not a zeros of polynomial $p(x) = 3x^2-1$

Q3 (viii) Verify whether the following are zeroes of the polynomial, indicated against it. $p(x) = 2x +1,\ x = \frac{1}{2}$

Answer:

Given polynomial is $p(x) = 2x+1$

Now, at $x = \frac{1}{2}$ it's value is

$p\left ( \frac{1}{2} \right )= 2 \times \left ( \frac{1}{2} \right )+1 = 1+1=2 \neq 0$

Therefore, $x = \frac{1}{2}$ is not a zeros of polynomial $p(x) = 2x+1$

Q4 (i) Find the zero of the polynomial in each of the following cases: $p(x)= x + 5$

Answer:

Given polynomial is $p(x)= x + 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow x+5 = 0$

$\Rightarrow x=-5$

Therefore, x = -5 is the zero of polynomial $p(x)= x + 5$

Q4 (ii) Find the zero of the polynomial in each of the following cases: $p(x) = x - 5$

Answer:

Given polynomial is $p(x)= x - 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow x-5 = 0$

$\Rightarrow x=5$

Therefore, x = 5 is a zero of polynomial $p(x)= x - 5$

Q4 (iii) Find the zero of the polynomial in each of the following cases: $p(x)= 2x + 5$

Answer:

Given polynomial is $p(x)= 2x + 5$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow 2x+5 = 0$

$\Rightarrow x=-\frac{5}{2}$

Therefore, $x=-\frac{5}{2}$ is a zero of polynomial $p(x)= 2x + 5$

Q4 (iv) Find the zero of the polynomial in each of the following cases: $p(x) = 3x - 2$

Answer:

Given polynomial is $p(x) = 3x - 2$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow 3x-2 = 0$

$\Rightarrow x=\frac{2}{3}$
Therefore, $x=\frac{2}{3}$ is a zero of polynomial $p(x) = 3x - 2$

Q4 (v) Find the zero of the polynomial in each of the following cases: $p(x) = 3x$

Answer:

Given polynomial is $p(x) = 3x$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow 3x = 0$

$\Rightarrow x=0$

Therefore, $x=0$ is a zero of polynomial $p(x) = 3x$

Q4 (vi) Find the zero of the polynomial in each of the following cases: $p(x) = ax, \ a\neq 0$

Answer:

Given polynomial is $p(x) = ax$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow ax = 0$

$\Rightarrow x=0$

Therefore, $x=0$ is a zero of polynomial $p(x) = ax$

Q4 (vii) Find the zero of the polynomial in each of the following cases: $p(x) = cx + d, c\neq 0, c,d$ are real numbers

Answer:

Given polynomial is $p(x) = cx+d$

Zero of a polynomial is that value of the variable at which the value of the polynomial is obtained as 0.

Now,

$p(x)=0$

$\Rightarrow cx+d = 0$

$\Rightarrow x=-\frac{d}{c}$

Therefore, $x=-\frac{d}{c}$ is a zero of polynomial $p(x) = cx+d$

Class 9 maths chapter 2 NCERT solutions Exercise: 2.3

Q1 (i) Find the remainder when $x^3 + 3x^2 +3x + 1$ is divided by $x + 1$

Answer:

When we divide $x^3 + 3x^2 +3x + 1$ by $x + 1$ .

By long division method, we will get

1639996048817
Therefore, remainder is $0$ .

Q1 (ii) Find the remainder when $x^3 + 3x^2 +3x + 1$ is divided by $x - \frac{1}{2}$

Answer:

When we divide $x^3 + 3x^2 +3x + 1$ by $x - \frac{1}{2}$ .

By long division method, we will get

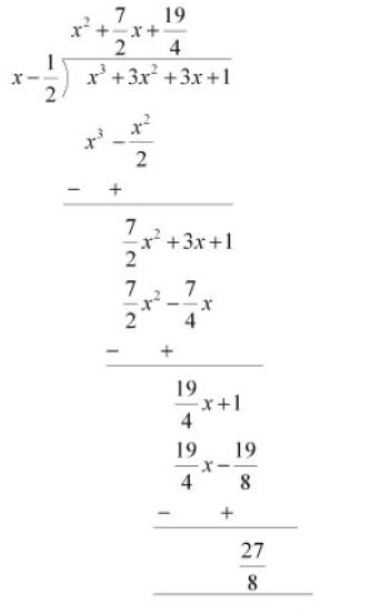1639996081431 Therefore, the remainder is $\frac{27}{8}$

Q1 (iii) Find the remainder when $x^3 + 3x^2 +3x + 1$ is divided by $x$

Answer:

When we divide $x^3 + 3x^2 +3x + 1$ by $x$ .

By long division method, we will get

1639996102222
Therefore, remainder is $1$ .

Q1 (iv) Find the remainder when $x^3 + 3x^2 +3x + 1$ is divided by $x + \pi$

Answer:

When we divide $x^3 + 3x^2 +3x + 1$ by $x + \pi$ .

By long division method, we will get

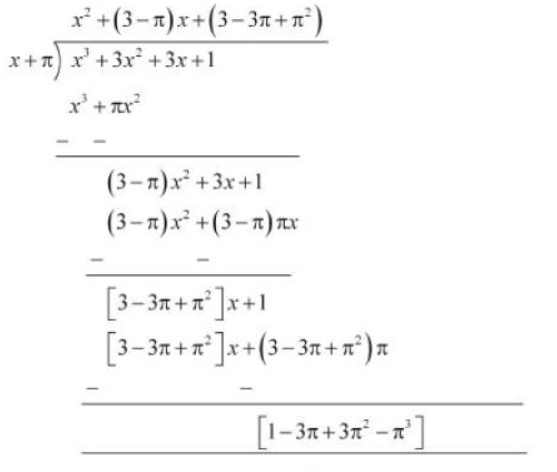
1639996129502
Therefore, the remainder is $1-3\pi + 3\pi^2-\pi^3$

Q1 (v) Find the remainder when $x^ 3 + 3x^ 2 + 3x + 1$ is divided by $5+2x$

Answer:

When we divide $x^3 + 3x^2 +3x + 1$ by $5+2x$ .

By long division method, we will get

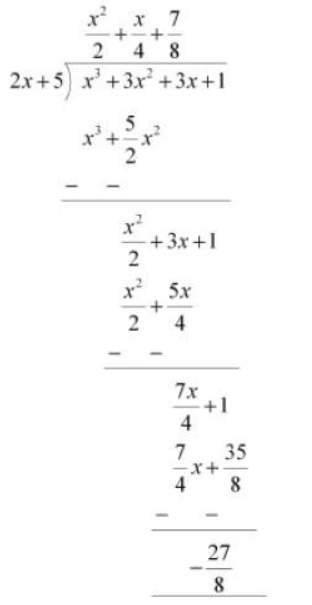
1639996167148
Therefore, the remainder is $-\frac{27}{8}$

Q2 Find the remainder when $x^3 - ax^2 + 6x - a$ is divided by $x - a$ .

Answer:

When we divide $x^3 - ax^2 + 6x - a$ by $x - a$ .

By long division method, we will get

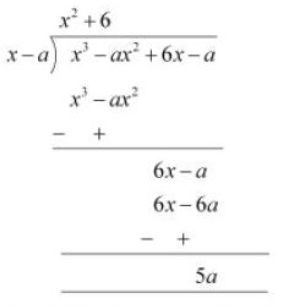
1639996211310
Therefore, remainder is $5a$

Q3 Check whether $7 + 3x$ is a factor of $3x^3 + 7x.$

Answer:

When we divide $3x^3 + 7x$ by $7 + 3x$ .

We can also write $3x^3 + 7x$ as $3x^3 +0x^2+ 7x$

By long division method, we will get

1639996248244
Since, remainder is not equal to 0

Therefore, $7 + 3x$ is not a factor of $3x^3 + 7x$

Class 9 polynomials NCERT solutions Exercise: 2.4

Q1 (i) Determine which of the following polynomials has $(x + 1)$ a factor : $x^3 + x^2 +x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p(x)=x^3 + x^2 +x + 1$

Then, $p(-1)$ must be equal to zero

Now,

$\Rightarrow p(-1)=(-1)^3+(-1)^2-1+1$

$\Rightarrow p(-1)=-1+1-1+1 = 0$

Therefore, $(x + 1)$ is a factor of polynomial $p(x)=x^3 + x^2 +x + 1$

Q1 (ii) Determine which of the following polynomials has $(x + 1)$ a factor : $x^4 + x^3 + x^2 +x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p(x)=x^4 + x^3 + x^2 +x + 1$

Then, $p(-1)$ must be equal to zero

Now,

$\Rightarrow p(-1)=(-1)^4+(-1)^3+(-1)^2-1+1$

$\Rightarrow p(-1)=1-1+1-1+1 = 1\neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p(x)=x^4 + x^3 + x^2 +x + 1$

Q1 (iii) Determine which of the following polynomials has $(x + 1)$ a factor : $x^4 + 3x^3 + 3x^2 +x + 1$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p(x)=x^4 + 3x^3 + 3x^2 +x + 1$

Then, $p(-1)$ must be equal to zero

Now,

$\Rightarrow p(-1)=(-1)^4+3(-1)^3+3(-1)^2-1+1$

$\Rightarrow p(-1)=1-3+3-1+1 = 1\neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p(x)=x^4 + 3x^3 + 3x^2 +x + 1$

Q1 (iv) Determine which of the following polynomials has $(x + 1)$ a factor : $x^3 - x^2 -(2 + \sqrt2)x + \sqrt2$

Answer:

Zero of polynomial $(x + 1)$ is -1.

If $(x + 1)$ is a factor of polynomial $p(x)=x^3 - x^2 -(2 + \sqrt2)x + \sqrt2$

Then, $p(-1)$ must be equal to zero

Now,

$\Rightarrow p(-1)=(-1)^3-(-1)^2-(2+\sqrt2)(-1)+\sqrt2$

$\Rightarrow p(-1)=-1-1+2+\sqrt2+\sqrt2 = 2\sqrt2\neq 0$

Therefore, $(x + 1)$ is not a factor of polynomial $p(x)=x^3 - x^2 -(2 + \sqrt2)x + \sqrt2$

Q2 (i) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x) = 2x^3 + x^2 - 2x - 1,\ g(x) = x + 1$

Answer:

Zero of polynomial $g(x)=x+1$ is $-1$

If $g(x)=x+1$ is factor of polynomial $p(x) = 2x^3 + x^2 - 2x - 1$

Then, $p(-1)$ must be equal to zero

Now,

$\Rightarrow p(-1)= 2(-1)^3+(-1)^2-2(-1)-1$

$\Rightarrow p(-1)= -2+1+2-1 = 0$

Therefore, $g(x)=x+1$ is factor of polynomial $p(x) = 2x^3 + x^2 - 2x - 1$

Q2 (ii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x) = x^3 + 3x^2 + 3x + 1, \ g(x) = x + 2$

Answer:

Zero of polynomial $g(x)=x+2$ is $-2$

If $g(x)=x+2$ is factor of polynomial $p(x) = x^3 + 3x^2 + 3x + 1$

Then, $p(-2)$ must be equal to zero

Now,

$\Rightarrow p(-2) = (-2)^3 + 3(-2)^2 + 3(-2) + 1$

$\Rightarrow p(-2)= -8+12-6+1 = -1\neq 0$

Therefore, $g(x)=x+2$ is not a factor of polynomial $p(x) = x^3 + 3x^2 + 3x + 1$

Q2 (iii) Use the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case: $p(x) = x^3 - 4x^2 + x + 6, \ g(x) = x - 3$

Answer:

Zero of polynomial $g(x)=x-3$ is $3$

If $g(x)=x-3$ is factor of polynomial $p(x) = x^3 - 4x^2 + x + 6$

Then, $p(3)$ must be equal to zero

Now,

$\Rightarrow p(3) = (3)^3 - 4(3)^2 + 3 + 6$

$\Rightarrow p(3) = 27-36+3+6=0$

Therefore, $g(x)=x-3$ is a factor of polynomial $p(x) = x^3 - 4x^2 + x + 6$

Q3 (i) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p(x) = x^2 + x + k$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p(x) = x^2 + x + k$

Then, $p(1)$ must be equal to zero

Now,

$\Rightarrow p(1) = (1)^2 + 1 + k$

$\Rightarrow p(1) =0$

$\Rightarrow 2+k = 0$

$\Rightarrow k = -2$

Therefore, value of k is $-2$

Q3 (ii) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p(x) = 2x^2 + kx + \sqrt2$

Answer:

Zero of the polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p(x) = 2x^2 + kx + \sqrt2$

Then, $p(1)$ must be equal to zero

Now,

$\Rightarrow p(1) = 2(1)^2 + k(1) + \sqrt2$

$\Rightarrow p(1) =0$

$\Rightarrow 2+k +\sqrt2= 0$

$\Rightarrow k = -(2+\sqrt2)$

Therefore, value of k is $-(2+\sqrt2)$

Q3 (iii) Find the value of k , if $x - 1$ is a factor of p(x) in the following case: $p(x) = kx^2-\sqrt2 x + 1$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p(x) = kx^2-\sqrt2 x + 1$

Then, $p(1)$ must be equal to zero

Now,

$\Rightarrow p(1) = k(1)^2 -\sqrt2(1) + 1$

$\Rightarrow p(1) =0$

$\Rightarrow k -\sqrt2 +1= 0$

$\Rightarrow k = -1+\sqrt2$

Therefore, value of k is $-1+\sqrt2$

Q3 (iv) the value of k , if $x - 1$ is a factor of p(x) in the following case: $p(x) = kx^2 -3 x + k$

Answer:

Zero of polynomial $x - 1$ is $1$

If $x - 1$ is factor of polynomial $p(x) = kx^2 -3 x + k$

Then, $p(1)$ must be equal to zero

Now,

$\Rightarrow p(1) = k(1)^2 -3(1) + k$

$\Rightarrow p(1) =0$

$\Rightarrow k -3+k= 0$

$\Rightarrow k = \frac{3}{2}$
Therefore, value of k is $\frac{3}{2}$

Q4 (i) Factorise : $12x^2 - 7x + 1$

Answer:

Given polynomial is $12x^2 - 7x + 1$

We need to factorise the middle term into two terms such that their product is equal to $12 \times 1 = 12$ and their sum is equal to $-7$

We can solve it as

$\Rightarrow 12x^2 - 7x + 1$

$\Rightarrow 12x^2-3x-4x+1$ $(\because -3 \times -4 = 12 \ \ and \ \ -3+(-4) = -7)$

$\Rightarrow 3x(4x-1)-1(4x-1)$

$\Rightarrow (3x-1)(4x-1)$

Q4 (ii) Factorise : $2x^2 + 7x + 3$

Answer:

Given polynomial is $2x^2 + 7x + 3$

We need to factorise the middle term into two terms such that their product is equal to $2 \times 3 = 6$ and their sum is equal to $7$

We can solve it as

$\Rightarrow 12x^2 - 7x + 1$

$\Rightarrow 2x^2+6x+x+3$ $(\because 6 \times 1 = 6 \ \ and \ \ 6+1 = 7)$

$\Rightarrow 2x(x+3)+1(x+3)$

$\Rightarrow (2x+1)(x+3)$

Q4 (iii) Factorise : $6x^2 +5x - 6$

Answer:

Given polynomial is $6x^2 +5x - 6$

We need to factorise the middle term into two terms such that their product is equal to $6 \times -6 =-3 6$ and their sum is equal to $5$

We can solve it as

$\Rightarrow 6x^2 +5x - 6$

$\Rightarrow 6x^2 +9x -4x - 6$ $(\because 9 \times -4 = -36 \ \ and \ \ 9+(-4) = 5)$

$\Rightarrow 3x(2x+3)-2(2x+3)$

$\Rightarrow (2x+3)(3x-2)$

Q4 (iv) Factorise : $3x^2 - x - 4$

Answer:

Given polynomial is $3x^2 - x - 4$

We need to factorise the middle term into two terms such that their product is equal to $3 \times -4 =-12$ and their sum is equal to $-1$

We can solve it as

$\Rightarrow 3x^2 - x - 4$

$\Rightarrow 3x^2 -4 x+3x - 4$ $(\because 3 \times -4 = -12 \ \ and \ \ 3+(-4) = -1)$

$\Rightarrow x(3x-4)+1(3x-4)$

$\Rightarrow (x+1)(3x-4)$

Q5 (i) Factorise : $x^3 - 2x^2 - x +2$

Answer:

Given polynomial is $x^3 - 2x^2 - x +2$

Now, by hit and trial method we observed that $(x+1)$ is one of the factors of the given polynomial.

By long division method, we will get

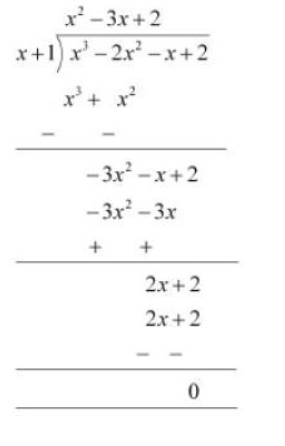1639996302612 We know that Dividend = (Divisor × Quotient) + Remainder

$x^3 - 2x^2 - x +2 = (x+1)(x^2-3x+2)+0$

$= (x+1)(x^2-2x-x+2)$

$= (x+1)(x-2)(x-1)$

Therefore, on factorization of $x^3 - 2x^2 - x +2$ we will get $(x+1)(x-2)(x-1)$

Q5 (ii) Factorise : $x^3 - 3x^2 -9x -5$

Answer:

Given polynomial is $x^3 - 3x^2 -9x -5$

Now, by hit and trial method we observed that $(x+1)$ is one of the factors of the given polynomial.

By long division method, we will get

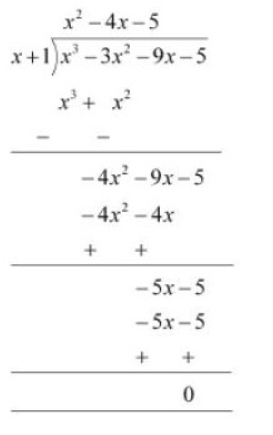1639996323635 We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^3 - 3x^2 -9x -5=(x+1)(x^2-4x-5)$

$= (x+1)(x^2-5x+x-5)$

$= (x+1)(x-5)(x+1)$

Therefore, on factorization of $x^3 - 3x^2 -9x -5$ we will get $(x+1)(x-5)(x+1)$

Q5 (iii) Factorise : $x^3 + 13x^2 + 32x + 20$

Answer:

Given polynomial is $x^3 + 13x^2 + 32x + 20$

Now, by hit and trial method we observed that $(x+1)$ is one of the factore of given polynomial.

By long division method, we will get

1639996347806 We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$x^3 + 13x^2 + 32x + 20=(x+1)(x^2+12x+20)$

$= (x+1)(x^2+10x+2x+20)$

$= (x+1)(x+10)(x+2)$

Therefore, on factorization of $x^3 + 13x^2 + 32x + 20$ we will get $(x+1)(x+10)(x+2)$

Q5 (iv) Factorise : $2y^3 + y^2 - 2y - 1$

Answer:

Given polynomial is $2y^3 + y^2 - 2y - 1$

Now, by hit and trial method we observed that $(y-1)$ is one of the factors of the given polynomial.

By long division method, we will get

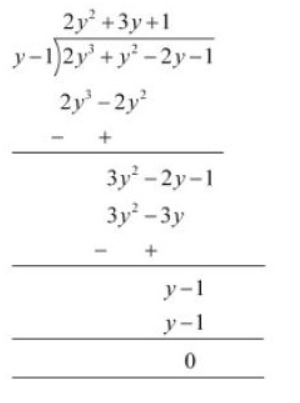1639996378575 We know that Dividend = (Divisor $\times$ Quotient) + Remainder

$2y^3 + y^2 - 2y - 1= (y-1)(2y^2+3y+1)$

$= (y-1)(2y^2+2y+y+1)$

$= (y-1)(2y+1)(y+1)$

Therefore, on factorization of $2y^3 + y^2 - 2y - 1$ we will get $(y-1)(2y+1)(y+1)$

Class 9 maths chapter 2 question answer Exercise: 2.5

Q1 (i) Use suitable identities to find the following product: $(x + 4) ( x + 10)$

Answer:

We will use identity

$(x+a)(x+b)=x^2+(a+b)x+ab$

Put $a = 4 \ \ and \ \ b = 10$

$(x+4)(x+10)= x^2+(10+4)x+10\times 4$

$= x^2+14x+40$

Therefore, $(x + 4) ( x + 10)$ is equal to $x^2+14x+40$

Q1 (ii) Use suitable identities to find the following product: $(x+8)(x-10)$

Answer:

We will use identity

$(x+a)(x+b)=x^2+(a+b)x+ab$

Put $a = 8 \ \ and \ \ b = -10$

$(x+8)(x-10)= x^2+(-10+8)x+8\times (-10)$

$= x^2-2x-80$

Therefore, $(x+8)(x-10)$ is equal to $x^2-2x-80$

Q1 (iii) Use suitable identities to find the following product: $(3x+4)(3x - 5)$

Answer:

We can write $(3x+4)(3x - 5)$ as

$(3x+4)(3x - 5)= 9\left ( x+\frac{4}{3} \right )\left ( x-\frac{5}{3} \right )$

We will use identity

$(x+a)(x+b)=x^2+(a+b)x+ab$

Put $a = \frac{4}{3} \ \ and \ \ b = -\frac{5}{3}$

$9\left ( x+\frac{4}{3} \right )\left ( x-\frac{5}{3} \right )= 9\left ( x^2+\left ( \frac{4}{3}-\frac{5}{3} \right )x+\frac{4}{3} \times \left ( -\frac{5}{3} \right ) \right )$

$=9x^2-3x-20$

Therefore, $(3x+4)(3x - 5)$ is equal to $9x^2-3x-20$

Q1 (iv) Use suitable identities to find the following product: $(y^2 + \frac{3}{2})(y^2 - \frac{3}{2})$

Answer:

We will use identity

$(x+a)(x-a)=x^2-a^2$

Put $x=y^2 \ \ and \ \ a = \frac{3}{2}$

$(y^2 + \frac{3}{2})(y^2 - \frac{3}{2}) = \left ( y^2 \right )^2-\left(\frac{3}{2} \right )^2$

$= y^4-\frac{9}{4}$

Therefore, $(y^2 + \frac{3}{2})(y^2 - \frac{3}{2})$ is equal to $y^4-\frac{9}{4}$

Q1 (v) Use suitable identities to find the following product: $(3 - 2x) (3 + 2x)$

Answer:

We can write $(3 - 2x) (3 + 2x)$ as

$(3 - 2x) (3 + 2x)=-4\left ( x-\frac{3}{2} \right )\left(x+\frac{3}{2} \right )$

We will use identity

$(x+a)(x-a)=x^2-a^2$

Put $a = \frac{3}{2}$

$-4(x + \frac{3}{2})(x- \frac{3}{2}) =-4\left ( \left ( x \right )^2-\left(\frac{3}{2} \right )^2 \right )$

$=9-4x^2$

Therefore, $(3 - 2x) (3 + 2x)$ is equal to $9-4x^2$

Q2 (i) Evaluate the following product without multiplying directly: $103 \times 107$

Answer:

We can rewrite $103 \times 107$ as

$\Rightarrow 103 \times 107= (100+3)\times (100+7)$

We will use identity

$(x+a)(x+b)=x^2+(a+b)x+ab$

Put $x =100 , a=3 \ \ and \ \ b = 7$

$(100+3)\times (100+7)= (100)^2+(3+7)100+3\times 7$

$=10000+1000+21= 11021$

Therefore, value of $103 \times 107$ is $11021$

Q2 (ii) Evaluate the following product without multiplying directly: $95 \times 96$

Answer:

We can rewrite $95 \times 96$ as

$\Rightarrow 95 \times 96= (100-5)\times (100-4)$

We will use identity

$(x+a)(x+b)=x^2+(a+b)x+ab$

Put $x =100 , a=-5 \ \ and \ \ b = -4$

$(100-5)\times (100-4)= (100)^2+(-5-4)100+(-5)\times (-4)$

$=10000-900+20= 9120$

Therefore, value of $95 \times 96$ is $9120$

Q2 (iii) Evaluate the following product without multiplying directly: $104 \times 96$

Answer:

We can rewrite $104 \times 96$ as

$\Rightarrow 104 \times 96= (100+4)\times (100-4)$

We will use identity

$(x+a)(x-a)=x^2-a^2$

Put $x =100 \ \ and \ \ a=4$

$(100+4)\times (100-4)= (100)^2-(4)^2$

$=10000-16= 9984$

Therefore, value of $104 \times 96$ is $9984$

Q3 (i) Factorise the following using appropriate identities: $9x^2 + 6xy + y^2$

Answer:

We can rewrite $9x^2 + 6xy + y^2$ as

$\Rightarrow 9x^2 + 6xy + y^2 = (3x)^2+2\times 3x\times y +(y)^2$

Using identity $\Rightarrow (a+b)^2 = (a)^2+2\times a\times b +(b)^2$

Here, $a= 3x \ \ and \ \ b = y$

Therefore,

$9x^2+6xy+y^2 = (3x+y)^2 = (3x+y)(3x+y)$

Q3 (ii) Factorise the following using appropriate identities: $4y^2 - 4y + 1$

Answer:

We can rewrite $4y^2 - 4y + 1$ as

$\Rightarrow 4y^2 - 4y + 1=(2y)^2-2\times2y\times 1+(1)^2$

Using identity $\Rightarrow (a-b)^2 = (a)^2-2\times a\times b +(b)^2$

Here, $a= 2y \ \ and \ \ b = 1$

Therefore,

$4y^2 - 4y + 1=(2y-1)^2=(2y-1)(2y-1)$

Q3 (iii) Factorise the following using appropriate identities: $x^2 - \frac{y^2}{100}$

Answer:

We can rewrite $x^2 - \frac{y^2}{100}$ as

$\Rightarrow x^2 - \frac{y^2}{100} = (x)^2-\left(\frac{y}{10} \right )^2$

Using identity $\Rightarrow a^2-b^2 = (a-b)(a+b)$

Here, $a= x \ \ and \ \ b = \frac{y}{10}$

Therefore,

$x^2 - \frac{y^2}{100} = \left ( x-\frac{y}{10} \right )\left ( x+\frac{y}{10} \right )$

Q4 (i) Expand each of the following, using suitable identities: $(x + 2y+4z)^2$

Answer:

Given is $(x + 2y+4z)^2$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a = x , b = 2y \ \ and \ \ c = 4z$

Therefore,

$(x + 2y+4z)^2 = (x)^2+(2y)^2+(4z)^2+2.x.2y+2.2y.4z+2.4z.x$

$= x^2+4y^2+16z^2+4xy+16yz+8zx$

Q4 (ii) Expand each of the following, using suitable identities: $(2x - y + z)^2$

Answer:

Given is $(2x - y + z)^2$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a = 2x , b = -y \ \ and \ \ c = z$

Therefore,

$(2x -y+z)^2 = (2x)^2+(-y)^2+(z)^2+2.2x.(-y)+2.(-y).z+2.z.2x$

$= 4x^2+y^2+z^2-4xy-2yz+4zx$

Q4 (iii) Expand each of the following, using suitable identities: $(-2x + 3y + 2z)^2$

Answer:

Given is $(-2x + 3y + 2z)^2$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a =- 2x , b = 3y \ \ and \ \ c = 2z$

Therefore,

$(-2x +3y+2z)^2 = (-2x)^2+(3y)^2+(2z)^2+2.(-2x).3y+2.3y.2z+2.z.(-2x)$

$= 4x^2+9y^2+4z^2-12xy+12yz-8zx$

Q4 (iv) Expand each of the following, using suitable identities: $(3a - 7b - c)^2$

Answer:

Given is $(3a - 7b - c)^2$

We will Use identity

$(x+y+z)^2=x^2+y^2+z^2+2xy+2yz+2zx$

Here, $x =3a , y = -7b \ \ and \ \ z = -c$

Therefore,

$(3a - 7b - c)^2=(3a)^2+(-7b)^2+(-c)^2+2.3a.(-7b)+2.(-7b).(-c)+2.(-c)$ $.3a$

$= 9a^2+49b^2+c^2-42ab+14bc-6ca$

Q4 (v) Expand each of the following, using suitable identities: $(-2x + 5y -3z)^2$

Answer:

Given is $(-2x + 5y -3z)^2$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a =- 2x , b = 5y \ \ and \ \ c = -3z$

Therefore,

$(-2x +5y-3z)^2$ $= (-2x)^2+(5y)^2+(-3z)^2+2.(-2x).5y+2.5y.(-3z)+2.(-3z).(-2x)$

$= 4x^2+25y^2+9z^2-20xy-30yz+12zx$

Q4 (vi) Expand each of the following, using suitable identities: $\left [\frac{1}{4}a - \frac{1}{2}b + 1\right ]^2$

Answer:

Given is $\left [\frac{1}{4}a - \frac{1}{2}b + 1\right ]^2$

We will Use identity

$(x+y+z)^2=x^2+y^2+z^2+2xy+2yz+2zx$

Here, $x =\frac{a}{4} , y = -\frac{b}{2} \ \ and \ \ z = 1$

Therefore,

$\left [\frac{1}{4}a - \frac{1}{2}b + 1\right ]^2$ $=\left(\frac{a}{4} \right )^2+\left(-\frac{b}{2} \right )^2+(1)^2+2.\left(\frac{a}{4} \right ). \left(-\frac{b}{2} \right )+2. \left(-\frac{b}{2} \right ).1+2.1.\left(\frac{a}{4} \right )$

$= \frac{a^2}{16}+\frac{b^2}{4}+1-\frac{ab}{4}-b+\frac{a}{2}$

Q5 (i) Factorise: $4x^2 +9y^2 +16z^2 + 12xy -24yz - 16xz$

Answer:

We can rewrite $4x^2 +9y^2 +16z^2 + 12xy -24yz - 16xz$ as

$\Rightarrow 4x^2 +9y^2 +16z^2 + 12xy -24yz - 16xz$ $= (2x)^2+(3y)^2+(-4z)^2+2.2x.3y+2.3y.(-4z)+2.(-4z).2x$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a = 2x , b = 3y \ \ and \ \ c = -4z$

Therefore,

$4x^2 +9y^2 +16z^2 + 12xy -24yz - 16xz = (2x+3y-4z)^2$

$= (2x+3y-4z)(2x+3y-4z)$

Q5 (ii) Factorise: $2x^2 + y^2 +8z^2 - 2\sqrt2 xy + 4\sqrt2 yz - 8xz$

Answer:

We can rewrite $2x^2 + y^2 +8z^2 - 2\sqrt2 xy + 4\sqrt2 yz - 8xz$ as

$\Rightarrow 2x^2 + y^2 +8z^2 - 2\sqrt2 xy + 4\sqrt2 yz - 8xz$ $= (-\sqrt2x)^2+(y)^2+(2\sqrt2z)^2+2.(-\sqrt2).y+2.y.2\sqrt2z+2.(-\sqrt2x).2\sqrt2z$

We will Use identity

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Here, $a = -\sqrt2x , b = y \ \ and \ \ c = 2\sqrt2z$

Therefore,

$2x^2 + y^2 +8z^2 - 2\sqrt2 xy + 4\sqrt2 yz - 8xz=(-\sqrt2x+y+2\sqrt2z)^2$

$=(-\sqrt2x+y+2\sqrt2z)(-\sqrt2x+y+2\sqrt2z)$

Q6 (i) Write the following cubes in expanded form: $(2x + 1)^3$

Answer:

Given is $(2x + 1)^3$

We will use identity

$(a+b)^3=a^3+b^3+3a^2b+3ab^2$

Here, $a= 2x \ \ and \ \ b= 1$

Therefore,

$(2x+1)^3=(2x)^3+(1)^3+3.(2x)^2.1+3.2x.(1)^2$

$= 8x^3+1+12x^2+6x$

Q6 (ii) Write the following cube in expanded form: $(2a-3b)^3$

Answer:

Given is $(2a-3b)^3$

We will use identity

$(x-y)^3=x^3-y^3-3x^2y+3xy^2$

Here, $x= 2a \ \ and \ \ y= 3b$

Therefore,

$(2a-3b)^3=(2a)^3-(3b)^3-3.(2a)^2.3b+3.2a.(3b)^2$

$= 8a^3-9b^3-36a^2b+54ab^2$

Q6 (iii) Write the following cube in expanded form: $\left[\frac{3}{2}x + 1\right ]^3$

Answer:

Given is $\left[\frac{3}{2}x + 1\right ]^3$

We will use identity

$(a+b)^3=a^3+b^3+3a^2b+3ab^2$

Here, $a= \frac{3x}{2} \ \ and \ \ b= 1$

Therefore,

$\left(\frac{3x}{2}+1 \right )^3= \left(\frac{3x}{2} \right )^3+(1)^3+3.\left(\frac{3x}{2} \right )^2.1+3.\frac{3x}{2}.(1)^2$

$= \frac{27x^3}{8}+1+\frac{27x^2}{4}+\frac{9x}{2}$

Q6 (iv) Write the following cube in expanded form: $\left[x - \frac{2}{3} y\right ]^3$

Answer:

Given is $\left[x - \frac{2}{3} y\right ]^3$

We will use identity

$(a-b)^3=a^3-b^3-3a^2b+3ab^2$

Here, $a=x \ and \ \ b= \frac{2y}{3}$

Therefore,

$\left[x - \frac{2}{3} y\right ]^3 = x^3-\left(\frac{2y}{3} \right )^3-3.x^2.\frac{2y}{3}+3.x.\left(\frac{2y}{3} \right )^2$

$= x^3-\frac{8y^3}{27}-2x^2y+\frac{4xy^2}{3}$

Q7 (i) Evaluate the following using suitable identities: $(99)^3$

Answer:

We can rewrite $(99)^3$ as

$\Rightarrow (99)^3=(100-1)^3$

We will use identity

$(a-b)^3=a^3-b^3-3a^2b+3ab^2$

Here, $a=100 \ and \ \ b= 1$

Therefore,

$(100-1)^1=(100)^3-(1)^3-3.(100)^2.1+3.100.1^2$

$= 1000000-1-30000+300= 970299$

Q7 (ii) Evaluate the following using suitable identities: $(102)^3$

Answer:

We can rewrite $(102)^3$ as

$\Rightarrow (102)^3=(100+2)^3$

We will use identity

$(a+b)^3=a^3+b^3+3a^2b+3ab^2$

Here, $a=100 \ and \ \ b= 2$

Therefore,

$(100+2)^1=(100)^3+(2)^3+3.(100)^2.2+3.100.2^2$

$= 1000000+8+60000+1200= 1061208$

Q7 (iii) Evaluate the following using suitable identities: $(998)^3$

Answer:

We can rewrite $(998)^3$ as

$\Rightarrow (998)^3=(1000-2)^3$

We will use identity

$(a-b)^3=a^3-b^3-3a^2b+3ab^2$

Here, $a=1000 \ and \ \ b= 2$

Therefore,

$(1000-2)^1=(1000)^3-(2)^3-3.(0100)^2.2+3.1000.2^2$

$= 1000000000-8-6000000+12000= 994011992$

Q8 (i) Factorise the following: $8a^3 + b^3 + 12a^2 b + 6ab^2$

Answer:

We can rewrite $8a^3 + b^3 + 12a^2 b + 6ab^2$ as

$\Rightarrow 8a^3 + b^3 + 12a^2 b + 6ab^2$ $= (2a)^3+(b)^3+3.(2a)^2.b+3.2a.(b)^2$

We will use identity

$(x+y)^3=x^3+y^3+3x^2y+3xy^2$

Here, $x=2a \ \ and \ \ y= b$

Therefore,

$8a^3 + b^3 + 12a^2 b + 6ab^2 = (2a+b)^3$

$=(2a+b)(2a+b)(2a+b)$

Q8 (ii) Factorise the following: $8a ^3 - b^3 - 12a^2 b + 6ab^2$

Answer:

We can rewrite $8a ^3 - b^3 - 12a^2 b + 6ab^2$ as

$\Rightarrow 8a ^3 - b^3 - 12a^2 b + 6ab^2$ $= (2a)^3-(b)^3-3.(2a)^2.b+3.2a.(b)^2$

We will use identity

$(x-y)^3=x^3-y^3-3x^2y+3xy^2$

Here, $x=2a \ \ and \ \ y= b$

Therefore,

$8a ^3 - b^3 - 12a^2 b + 6ab^2 =(2a-b)^3$

$=(2a-b)(2a-b)(2a-b)$

Q8 (iii) Factorise the following: $27 - 125a^ 3 - 135a + 225a^2$

Answer:

We can rewrite $27 - 125a^ 3 - 135a + 225a^2$ as

$\Rightarrow 27 - 125a^ 3 - 135a + 225a^2^{}$ $= (3)^3-(25a)^3-3.(3)^2.5a+3.3.(5a)^2$

We will use identity

$(x-y)^3=x^3-y^3-3x^2y+3xy^2$

Here, $x=3 \ \ and \ \ y= 5a$

Therefore,

$27 - 125a^ 3 - 135a + 225a^2 = (3-5a)^3$

$=(3-5a)(3-5a)(3-5a)$

Q8 (iv) Factorise the following: $64a^3 - 27b^3 - 144a^2 b + 108ab^2$

Answer:

We can rewrite $64a^3 - 27b^3 - 144a^2 b + 108ab^2$ as

$\Rightarrow 64a^3 - 27b^3 - 144a^2 b + 108ab^2$ $= (4a)^3-(3b)^3-3.(4a)^2.3b+3.4a.(3b)^2$

We will use identity

$(x-y)^3=x^3-y^3-3x^2y+3xy^2$

Here, $x=4a \ \ and \ \ y= 3b$

Therefore,

$64a^3 - 27b^3 - 144a^2 b + 108ab^2=(4a-3b)^2$

$=(4a-3b)(4a-3b)(4a-3b)$

Q8 (v) Factorise the following: $27p^3 - \frac{1}{216} - \frac{9}{2}p^2 + \frac{1}{4} p$

Answer:

We can rewrite $27p^3 - \frac{1}{216} - \frac{9}{2}p^2 + \frac{1}{4} p$ as

$\Rightarrow 27p^3 - \frac{1}{216} - \frac{9}{2}p^2 + \frac{1}{4} p$ $= (3p)^3-\left(\frac{1}{6} \right )^3-3.(3p)^2.\frac{1}{6}+3.3p.\left(\frac{1}{6} \right )^2$

We will use identity

$(x-y)^3=x^3-y^3-3x^2y+3xy^2$

Here, $x=3p \ \ and \ \ y= \frac{1}{6}$

Therefore,

$27p^3 - \frac{1}{216} - \frac{9}{2}p^2 + \frac{1}{4} p = \left ( 3p-\frac{1}{6} \right )^3$

$= \left ( 3p-\frac{1}{6} \right ) \left ( 3p-\frac{1}{6} \right ) \left ( 3p-\frac{1}{6} \right )$

Q9 (i) Verify: $x^3 + y^3 = (x +y)(x^2 - xy + y^2)$

Answer:

We know that

$(x+y)^3=x^3+y^3+3xy(x+y)$

Now,

$\Rightarrow x^3+y^3=(x+y)^3-3xy(x+y)$

$\Rightarrow x^3+y^3=(x+y)\left((x+y)^2-3xy \right )$

$\Rightarrow x^3+y^3=(x+y)\left(x^2+y^2+2xy-3xy \right )$ $(\because (a+b)^2=a^2+b^2+2ab)$

$\Rightarrow x^3+y^3=(x+y)\left(x^2+y^2-xy \right )$

Hence proved.

Q9 (ii) Verify: $x^3 - y^3 = (x -y)(x^2 + xy + y^2)$

Answer:

We know that

$(x-y)^3=x^3-y^3-3xy(x-y)$

Now,

$\Rightarrow x^3-y^3=(x-y)^3+3xy(x-y)$

$\Rightarrow x^3-y^3=(x-y)\left((x-y)^2+3xy \right )$

$\Rightarrow x^3-y^3=(x-y)\left(x^2+y^2-2xy+3xy \right )$ $(\because (a-b)^2=a^2+b^2-2ab)$

$\Rightarrow x^3-y^3=(x-y)\left(x^2+y^2+xy \right )$

Hence proved.

Q10 (i) Factorise the following: $27y^3 + 125z^3$

Answer:

We know that

$a^3+b^3=(a+b)(a^2+b^2-ab)$

Now, we can write $27y^3 + 125z^3$ as

$\Rightarrow 27y^3 + 125z^3 = (3y)^3+(5z)^3$

Here, $a = 3y \ \ and \ \ b = 5z$

Therefore,

$27y^3+125z^3= (3y+5z)\left((3y)^2+(5z)^2-3y.5z \right )$

$27y^3+125z^3= (3y+5z)\left(9y^2+25z^2-15yz \right )$

Q10 (ii) Factorise the following: $64m^3 - 343n^3$

Answer:

We know that

$a^3-b^3=(a-b)(a^2+b^2+ab)$

Now, we can write $64m^3 - 343n^3$ as

$\Rightarrow 64m^3 - 343n^3 = (4m)^3-(7n)^3$

Here, $a = 4m \ \ and \ \ b = 7n$

Therefore,

$64m^3-343n^3= (4m-7n)\left((4m)^2+(7n)^2+4m.7n \right )$

$64m^3-343n^3= (4m-7n)\left(16m^2+49n^2+28mn \right )$

Q11 Factorise: $27x^3 + y^3 + z^3 - 9xyz$

Answer:

Given is $27x^3 + y^3 + z^3 - 9xyz$

Now, we know that

$a^3+b^3+c^3-3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)$

Now, we can write $27x^3 + y^3 + z^3 - 9xyz$ as

$\Rightarrow 27x^3 + y^3 + z^3 - 9xyz$ $=(3x)^3+(y)^3+(z)^3-3.3x.y.z$

Here, $a= 3x , b = y \ \ and \ \ c = z$

Therefore,

$27x^3 + y^3 + z^3 - 9xyz$ $=(3x+y+z)\left((3x)^2+(y)^2+(z)^2-3x.y-y.z-z.3x \right )$

$=(3x+y+z)\left(9x^2+y^2+z^2-3xy-yz-3zx \right )$

Q12 Verify that $x^3 + y^3 + z^3 -3xyz = \frac{1}{2} ( x + y + z)\left[(x-y)^2 + (y-z)^2 + (z-x)^2 \right ]$

Answer:

We know that

$x^3+y^3+z^3-3xyz = (x+y+z)(x^2+y^2+z^2-xy-yz-zx)$

Now, multiply and divide the R.H.S. by 2

$x^3+y^3+z^3-3xyz = \frac{1}{2}(x+y+z)(2x^2+2y^2+2z^2-2xy-2yz-2zx)$

$= \frac{1}{2}(x+y+z)(x^2+y^2-2xy+x^2+z^2-2zx+y^2+z^2-2yz)$

$= \frac{1}{2}(x+y+z)\left((x-y)^2+(y-z)^2 +(z-x)^2\right )$ $\left(\because a^2+b^2-2ab=(a-b)^2 \right )$

Hence proved.

Q13 If $x + y + z = 0$ , show that $x^3 + y^3 + z^3 = 3xyz$ .

Answer:

We know that

$x^3+y^3+z^3-3xyz = (x+y+z)(x^2+y^2+z^2-xy-yz-zx)$

Now, It is given that $x + y + z = 0$

Therefore,

$x^3+y^3+z^3-3xyz =0(x^2+y^2+z^2-xy-yz-zx)$

$x^3+y^3+z^3-3xyz =0$

$x^3+y^3+z^3=3xyz$

Hence proved.

Q14 (i) Without actually calculating the cubes, find the value of each of the following: $(-12)^3 + (7)^3 + (5)^3$

Answer:

Given is $(-12)^3 + (7)^3 + (5)^3$

We know that

If $x+y+z = 0$ then , $x^3+y^3+z^3 = 3xyz$

Here, $x = -12 , y = 7 \ \ an d \ \ z = 5$

$\Rightarrow x+y+z = -12+7+5 = 0$

Therefore,

$(-12)^3 + (7)^3 + (5)^3 = 3 \times (-12)\times 7 \times 5 = -1260$

Therefore, value of $(-12)^3 + (7)^3 + (5)^3$ is $-1260$

Q14 (ii) Without actually calculating the cubes, find the value of the following: $(28)^3 + (-15)^3 + (-13)^3$

Answer:

Given is $(28)^3 + (-15)^3 + (-13)^3$

We know that

If $x+y+z = 0$ then , $x^3+y^3+z^3 = 3xyz$

Here, $x = 28 , y = -15 \ \ an d \ \ z = -13$

$\Rightarrow x+y+z =28-15-13 = 0$

Therefore,

$(28)^3 + (-15)^3 + (-13)^3 = 3 \times (28)\times (-15) \times (-13) = 16380$

Therefore, value of $(28)^3 + (-15)^3 + (-13)^3$ is $16380$

Q15 (i) Give possible expressions for the length and breadth of the following rectangle, in which its area is given:

$25a^2 - 35a + 12$

Answer:

We know that

Area of rectangle is = $length \times breadth$

It is given that area = $25a^2-35a+12$

Now, by splitting middle term method

$\Rightarrow 25a^2-35a+12 = 25a^2-20a-15a+12$

$= 5a(5a-4)-3(5a-4)$

$= (5a-3)(5a-4)$
Therefore, two answers are possible

case (i) :- Length = $(5a-4)$ and Breadth = $(5a-3)$

case (ii) :- Length = $(5a-3)$ and Breadth = $(5a-4)$

Q15 (ii) Give possible expressions for the length and breadth of the following rectangle, in which its area is given:

$35y^2 + 13y- 12$

Answer:

We know that

Area of rectangle is = $length \times breadth$

It is given that area = $35y^2 + 13y- 12$

Now, by splitting the middle term method

$\Rightarrow 35y^2 + 13y- 12 =35y^2+28y-15y-12$

$= 7y(5y+4)-3(5y+4)$

$= (7y-3)(5y+4)$

Therefore, two answers are possible

case (i) :- Length = $(5y+4)$ and Breadth = $(7y-3)$

case (ii) :- Length = $(7y-3)$ and Breadth = $(5y+4)$

Q16 (i) What are the possible expressions for the dimensions of the cuboid whose volumes is given below?

Volume : $3x^2 - 12x$

Answer:

We know that

Volume of cuboid is = $length \times breadth \times height$

It is given that volume = $3x^2-12x$

Now,

$\Rightarrow 3x^2-12x=3\times x\times (x-4)$

Therefore,one of the possible answer is possible

Length = $3$ and Breadth = $x$ and Height = $(x-4)$

Q16 (ii) What are the possible expressions for the dimensions of the cuboid whose volumes is given below?

Volume : $12ky^2 + 8ky - 20k$

Answer:

We know that

Volume of cuboid is = $length \times breadth \times height$

It is given that volume = $12ky^2+8ky-20k$

Now,

$\Rightarrow 12ky^2+8ky-20k = k(12y^2+8y-20)$

$= k(12y^2+20y-12y-20)$

$= k\left(4y(3y+5)-4(3y+5) \right )$

$= k(3y+5)(4y-4)$

$= 4k(3y+5)(y-1)$

Therefore,one of the possible answer is possible

Length = $4k$ and Breadth = $(3y+5)$ and Height = $(y-1)$

NCERT Solutions for Class 9 Maths Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Number Systems
Chapter 2	Polynomials
Chapter 3	Coordinate Geometry
Chapter 4	Linear Equations In Two Variables
Chapter 5	Introduction to Euclid's Geometry
Chapter 6	Lines And Angles
Chapter 7	Triangles
Chapter 8	Quadrilaterals
Chapter 9	Areas of Parallelograms and Triangles
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Heron’s Formula
Chapter 13	Surface Area and Volumes
Chapter 14	Statistics
Chapter 15	Probability

Key Features of NCERT Solutions For chapter 2 maths class 9

Comprehensive coverage of topics related to Polynomials in one variable, Zeros of a Polynomial, Real Numbers and their Decimal Expansions, and more.
Maths chapter 2 class 9 solutions are designed in a clear and concise language to help students understand the concepts with ease.
The step-by-step approach of the ch 2 maths class 9 solutions assists students in learning and solving mathematical problems in a structured manner.
Inclusion of a wide range of solved examples and exercises to aid students in practicing and assessing their understanding of the concepts.

The class 9 chapter 2 maths solutions are prepared by experts at Careers360 who have extensive knowledge and experience in Mathematics.

NCERT Solutions for Class 9 Subject Wise

NCERT Solutions for Class 9 Maths

NCERT Solutions for Class 9 Science

How to Use NCERT Solutions For Class 9 Maths Chapter 2 Polynomials?

First of all, learn some basics and concepts regarding chapter Polynomials.
While reading the basics, go through the examples so that you can understand the applications of the concepts.
Once you have done the above two points, then you can directly move to the practice exercises.
While practising the exercises, if you stuck anywhere then you can take the help of the NCERT solutions for Class 9 Maths chapter 2 Polynomials.
After the completion of practice exercises, you can go through some previous year question papers.

NCERT Books and NCERT Syllabus

Keep Working Hard and Happy Learning!

Frequently Asked Questions (FAQs)

1. What are the important topics in NCERT Class 9 syllabus chapter Polynomials ?

The NCERT class 9 maths chapter 2 includes topics such as definition of a polynomial, zeroes, coefficient, degrees, and terms of a polynomial, different types of a polynomial, remainder and factor theorems, and the factorization of polynomials. students should practice these NCERT solutions to get indepth understanding of these concepts which ultimately lead to score well in the exam.

2. What is the number of exercises included in NCERT Solutions for class 9 maths polynomials?

Maths chapter 2 includes five exercises covering topics such as Polynomials in one variable, Zeros of a Polynomial, Real Numbers and their Decimal Expansions, Representing Real Numbers on the Number Line, Operations on Real Numbers, and Laws of Exponents for Real Numbers. Practicing these exercises of NCERT maths class 9 chapter 2 is crucial for achieving a better understanding of the concepts and scoring well in Mathematics. To help students gain confidence, Careers360 experts have designed these solutions to provide comprehensive explanations of the concepts covered in this chapter.

3. What are the advantages of choosing NCERT Solutions for Class 9 Maths Chapter 2?

NCERT Solutions for Class 9 Maths Chapter 2 use straightforward language to explain the concepts, making it accessible even for students who struggle with Mathematics. These solutions are meticulously crafted by a team of experts at Careers360 with the objective of helping students prepare for their CBSE exams effectively.

4. Is it challenging to grasp the concepts in NCERT Solutions for polynomials class 9 solutions?

Regular practice with NCERT Solutions for Class 9 Maths Chapter 2 can enable students to excel in their CBSE exams. These solutions are created by a team of skilled Maths experts at Careers360, and by solving all the questions and comparing their answers with the solutions, students can aim for high scores in their exams.

5. Where can I find the complete solutions of NCERT for Class 9 Maths ?

Here, students can get detailed NCERT solutions for Class 9 Maths which includes solutions to all the exercise of each chapters.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

Polynomials Class 9 Questions And Answers PDF Free Download

Polynomials Class 9 Solutions - Important Formulae

Polynomials Class 9 NCERT Solutions (Intext Questions and Exercise)

More About NCERT Solutions For Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter Wise

Key Features of NCERT Solutions For chapter 2 maths class 9

NCERT Solutions for Class 9 Subject Wise

How to Use NCERT Solutions For Class 9 Maths Chapter 2 Polynomials?

NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app