NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

Edited By Ramraj Saini | Updated on May 08, 2023 02:50 PM IST

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

Heron's Formula Class 9 Questions And Answers are provided here. These NCERT solutions are created by expert team at Careers360 keeping in mind latest CBSE syllabus 2023-23. Practicing these solutions give you confidence during the exam which ultimately lead to score well in the exam. In this particular NCERT book chapter 12 maths class 9, you will learn a special technique to find the area of any triangle. NCERT Solutions for class 9 maths chapter 12 Heron's Formula is covering the explanation of all questions using Heron's formula.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
Herons Formula Class 9 Questions And Answers PDF Free Download
Herons Formula Class 9 Solutions - Important Formulae
Herons Formula Class 9 NCERT Solutions (Intext Questions and Exercise)
Summary Of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
NCERT solutions for class 9 maths - chapter wise
Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
NCERT solutions for class 9 subject wise

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

Class 9 herons formula NCERT solutions are covering the solutions to each and every question present in the practice exercises in detail. If three sides of triangles are a, b, and c then the area in terms of a, b and c is given by the Heron's Formula class 9. The area is given by the formula 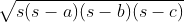$\sqrt{s(s-a)(s-b)(s-c)}$ where s is half the perimeter. That is $s=\frac{a+b+c}{2}$ . You may think about the application of Heron's Formula. This formula is used for calculating the area of irregular plots. If you have a land whose shape is not regular we will divide the plots into different triangles and then apply Heron's Formula class 9 to calculate the area. Here you will get NCERT solutions for class 9 also.

Also read:

Herons Formula Class 9 Questions And Answers PDF Free Download

Download PDF

Herons Formula Class 9 Solutions - Important Formulae

Triangle:

Semi-perimeter of a triangle = s = (a + b + c)/2,

Where 's' is the semi-perimeter, and 'a', 'b', and 'c' are the lengths of its sides.

Area = √[s(s - a)(s - b)(s - c)]

Equilateral Triangle:

For an equilateral triangle with side length 'a':

Its perimeter is given by: Perimeter = 3a units.
The altitude (height) of an equilateral triangle is equal to √3/2 times its side length, Altitude = √3/2 * units.
The area of an equilateral triangle is equal to √3/4 times the square of its side length, Area = √3/4 * a^2 units. These formulas are specific to equilateral triangles and are based on their unique properties.

Free download NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula for CBSE Exam.

Herons Formula Class 9 NCERT Solutions (Intext Questions and Exercise)

Class 9 maths chapter 12 question answer - exercise: 12.1

Q1 A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘ a ’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Answer:

Given the perimeter of an equilateral triangle is 180cm.

So, $3a = 180\ cm$ or $a = 60\ cm$ .

Hence, the length of the side is 60cm.

Now,

Calculating the area of the signal board by the Heron's Formula:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

Where, s is the half-perimeter of the triangle and a, b and c are the sides of the triangle.

Therefore,

$s = \frac{1}{2}Perimeter = \frac{1}{2}180cm = 90cm$

$a =b=c = 60cm$ as it is an equilateral triangle.

Substituting the values in the Heron's formula, we obtain

$\implies A = \sqrt{90(90-60)(90-60)(90-60)} = 900\sqrt{3}\ cm^2$ .

Q2 The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of Rs. 5000 per m ² per year. A company hired one of its walls for 3 months. How much rent did it pay?

1640600558297 Answer:

From the figure,

The sides of the triangle are:

$a = 122m,\ b = 120m\ and\ c = 22m$

The semi perimeter, s will be

$s = \frac{a+b+c}{2} = \frac{122+120+22}{2} = \frac{264}{2} = 132m$

Therefore, the area of the triangular side wall will be calculated by the Heron's Formula,

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{132(132-122)(132-120)(132-22)}\ m^2$

$= \sqrt{132(10)(12)(110)}\ m^2$

$= \sqrt{(12\times11)(10)(12)(11\times10)}\ m^2 = 1320\ m^2$

Given the rent for 1 year (i.e., 12 months) per meter square is Rs. 5000.

Rent for 3 months per meter square will be:

$Rs.\ 5000\times \frac{3}{12}$

Therefore, for 3 months for 1320 m ² :

$Rs.\ 5000\times \frac{3}{12}\times 1320 = Rs.\ 16,50,000.$

Q3 There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

1640600584782 Answer:

Given the sides of the triangle are:

$a = 15 m,\ b= 11m\ and\ c= 6m.$

So, the semi perimeter of the triangle will be:

$s = \frac{a+b+c}{2} = \frac{15+11+6}{2} = \frac{32}{2} = 16m$

Therefore, Heron's formula will be:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{16(16-15)(16-11)(16-6)}$

$= \sqrt{16(1)(5)(10)}$

$= \sqrt{(4\times 4)(1)(5)(5\times 2 )}$

$= 4\times 5 \sqrt2 = 20\sqrt2\ m^2$

Hence, the area painted in colour is $20\sqrt2\ m^2$ .

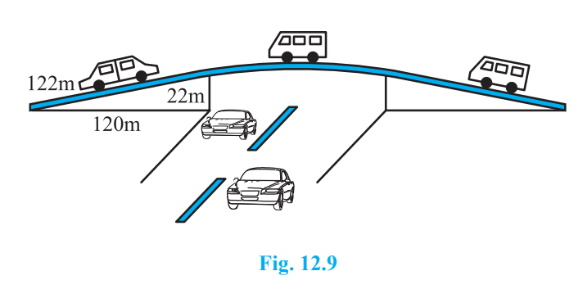
Q4 Find the area of a triangle two sides of which are 18cm and 10cm and the perimeter is 42cm.

Answer:

Given the perimeter of the triangle is $42cm$ and the sides length $a= 18cm$ and $b= 10cm$

So, $a+b+c = 42cm$

Or, $c = 42 - 18-10 = 14cm$

So, the semi perimeter of the triangle will be:

$s = \frac{P}{2} = \frac{42cm}{2} = 21cm$

Therefore, the area given by the Heron's Formula will be,

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{21(21-18)(21-10)(21-14)}$

$= \sqrt{(7\times3 )(3)(11)(7)}$

$= 21\sqrt{11}\ cm^2$

Hence, the area of the triangle is $21\sqrt{11}\ cm^2.$

Q5 Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.

Answer:

Given the sides of a triangle are in the ratio of $12:17:25$ and its perimeter is $540cm$

Let us consider the length of one side of the triangle be $a = 12x$

Then, the remaining two sides are $b = 17x$ and $c = 25x.$

So, by the given perimeter, we can find the value of x:

$Perimeter = a+b+c = 12x+17x+25x = 540cm$

$\implies 54x = 540cm$

$\implies x = 10$

So, the sides of the triangle are:

$a = 12\times10 =120 cm$

$b = 17\times10 =170 cm$

$c = 25\times10 =250 cm$

So, the semi perimeter of the triangle is given by

$s = \frac{540cm}{2} = 270cm$

Therefore, using Heron's Formula, the area of the triangle is given by

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{270(270-120)(270-170)(270-250)}$

$= \sqrt{270(150)(100)(20)}$

$= \sqrt{81000000} = 9000cm^2$

Hence, the area of the triangle is $9000cm^2$ .

Q6 An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Answer:

The perimeter of an isosceles triangle is 30 cm (Given).

The length of the sides which are equal is12 cm.

Let the third side length be 'a cm'.

Then, $Perimeter = a+b+c$

$\Rightarrow 30= a+12+12$

$\Rightarrow a = 6cm$

So, the semi-perimeter of the triangle is given by,

$s= \frac{1}{2}Perimeter =\frac{1}{2}\times30cm = 15cm$

Therefore, using Herons' Formula, calculating the area of the triangle

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{15(15-6)(15-12)(15-12)}$

$= \sqrt{15(9)(3)(3)}$

$= 9\sqrt{15}\ cm^2$

Hence, the area of the triangle is $9\sqrt{15}cm^2.$

Class 9 maths chapter 12 NCERT solutions - exercise : 12.2

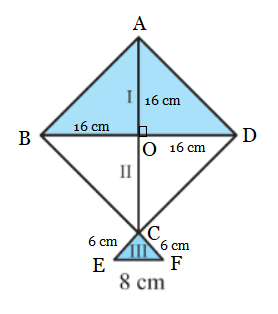
Q1 A park, in the shape of a quadrilateral ABCD, has $\angle C = 90\degree$ , $AB = 9 m$ , $BC = 12 m$ , $CD = 5 m$ and $AD = 8 m$ . How much area does it occupy?

Answer:

From the figure:

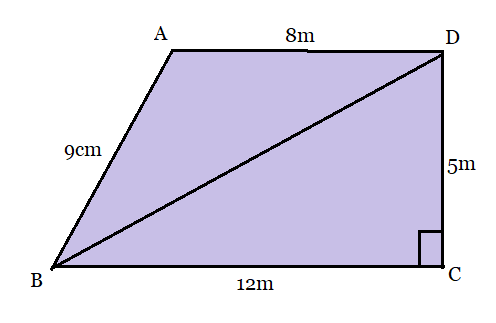
1640600614678

We have joined the BD to form two triangles so that the calculation of the area will be easy.

In triangle BCD, by Pythagoras theorem

$BD^2 = BC^2+CD^2$

$\Rightarrow BD^2 = 12^2+5^2 = 144+25 = 169$

$\Rightarrow BD = 13\ cm$

The area of triangle BCD can be calculated by,

$Area_{(BCD)} = \frac{1}{2}\times BC\times DC = \frac{1}{2}\times 12\times 5 = 30\ cm^2$

and the area of the triangle DAB can be calculated by Heron's Formula:

So, the semi-perimeter of the triangle DAB,

$s = \frac{a+b+c}{2} = \frac{9+8+13}{2} = \frac{30}{2} = 15\ cm$

Therefore, the area will be:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

where, $a = 9 cm,\ b = 8cm\ and\ c = 13cm$ .

$= \sqrt{15(15-9)(15-8)(15-13)}$

$= \sqrt{12(6)(7)(2)} = \sqrt{1260} = 35.5\ cm^2$ (Approximately)

Then, the total park area will be:

$= Area\ of\ triangle\ BCD + Area\ of\ triangle\ DAB$

$\Rightarrow$ $Total\ area\ of\ Park = 30+35.35 = 65.5\ cm^2$

Hence, the total area of the park is $65.5\ cm^2.$

Q2 Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Answer:

From the figure:

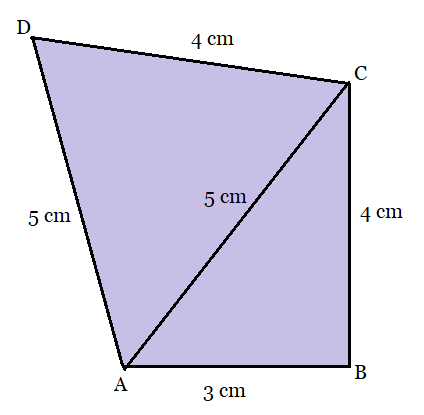
1640600632801

We have joined the AC to form two triangles so that the calculation of the area will be easy.

The area of the triangle ABC can be calculated by Heron's formula:

So, the semi-perimeter, where $a = 3 cm,\ b =4cm\ and\ c = 5cm.$

$s = \frac{a+b+c}{2} = \frac{3+4+5}{2} = 6cm$

Heron's Formula for calculating the area:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{6(6-3)(6-4)(6-5)}= \sqrt{6(3)(2)(1)} = \sqrt{36} = 6\ cm^2$

And the sides of the triangle ACD are $a' =4cm,\ b' = 5cm\ and\ c' = 5cm.$

So, the semi-perimeter of the triangle:

$s' = \frac{a'+b'+c'}{2} = \frac{4+5+5}{2} = \frac{14}{2} = 7cm$

Therefore, the area will be given by, Heron's formula

$A = \sqrt{s'(s'-a')(s'-b')(s'-c')}$ .

$= \sqrt{7(7-4)(7-5)(7-5)}$

$= \sqrt{7(3)(2)(2)} = 2\sqrt{21} = 9.2\ cm^2\ \ \ \ (Approx.)$

Then, the total area of the quadrilateral will be:

$= Area\ of\ triangle\ ABC + Area\ of\ triangle\ ACD$

$\Rightarrow$ $Total\ area\ of\ quadrilateral\ ABCD = 6+9.2 = 15.2\ cm^2$

Hence, the area of the quadrilateral ABCD is $15.2 \ cm^2.$

Q3 Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

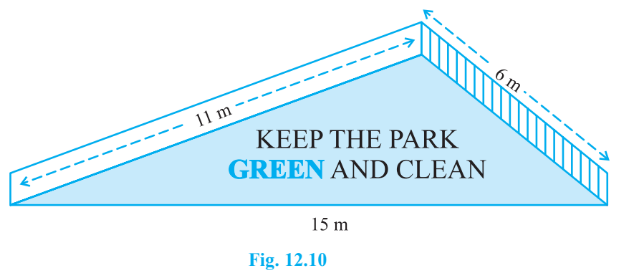
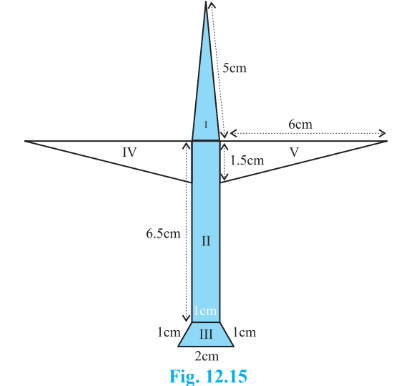1640600656571 Answer:

The total area of the paper used will be the sum of the area of the sections I, II, III, IV, and V. i.e., $Total\ area = I +II+III+IV+V$

For section I:

Here, the sides are $a = 1cm\ and\ b =c = 5cm.$

So, the Semi-perimeter will be:

$s = \frac{a+b+c}{2} = \frac{5+5+1}{2} = 5.5\ cm$

Therefore, the area of section I will be given by Heron's Formula,

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{5.5(5.5-1)(5.5-5)(5.5-5)}$

$= \sqrt{5.5(4.5)(0.5)(0.5)} = \sqrt{6.1875} = 2.5\ cm^2\ \ \ \ \ \ (Approx.)$

For section II:

Here the sides of the rectangle are $l =6.5\ cm$ and $b =1 \ cm.$

Therefore, the area of the rectangle is $= l\times b = 6.5\times 1 = 6.5\ cm^2.$

For section III:

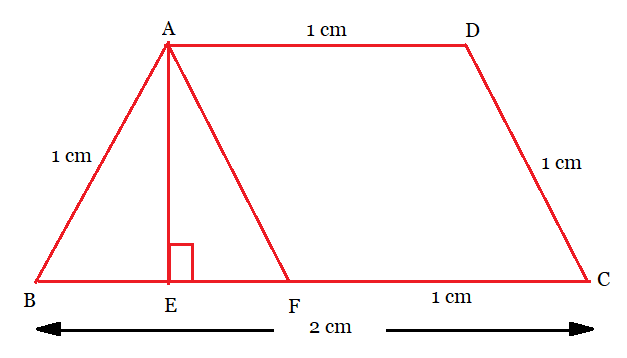
1640600697563

From the figure:

Drawing the parallel line AF to DC and a perpendicular line AE to BC.

We have the quadrilateral ADCF,

$AF || DC$ ...........................by construction.

$AD || FC$ ...........................[ $\because$ ABCD is a trapezium]

So, ADCF is a parallelogram.

Therefore, $AF = DC = 1\ cm$ and $AD = FC = 1\ cm$

$\left [ \because Opposite\ sides\ of\ a\ parallelogram \right ]$

Therefore, $BF = BC -FC =2-1 = 1\ cm.$

$\implies$ ABF is an equilateral triangle. $\left [ \because AB = BF =AF = 1\ cm \right ]$

Then, the area of the equilateral triangle ABF is given by:

$\implies \frac{\sqrt3}{4}a^2 = \frac{\sqrt3}{4}1^2 = \frac{\sqrt3}{4}$

$= \frac{1}{2}\times BF \times AE$

$= \frac{1}{2}\times 1cm \times AE = \frac{\sqrt3}{4}$

$\implies AE = \frac{\sqrt3}{2} = \frac{1.732}{2} = 0.866 \approx 0.9$

Hence, the area of trapezium ABCD will be:

$= \frac{1}{2}\times(AD+BC)\times AE$

$= \frac{1}{2}\times(1+2)\times 0.9$

$=1.35 =1.4\ cm^2\ \ \ \ (Approx.)$

For Section IV:

Here, the base is 1.5 cm and the height is 6 cm.

Therefore, the area of the triangle is :

$= \frac{1}{2}\times base\times height$

$= \frac{1}{2}\times 1.5\times 6 = 4.5\ cm^2$

For section V:

The base length = 1.5cm and the height is 6cm.

Therefore, the area of the triangle will be:

$= \frac{1}{2}\times 1.5\times 6 = 4.5\ cm^2$

Hence, the total area of the paper used will be:

$Total\ area = I +II+III+IV+V$

$= 2.5+6.5+1.4+4.5+4.5 = 19.4\ cm^2$

Q4 A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Answer:

From the figure:

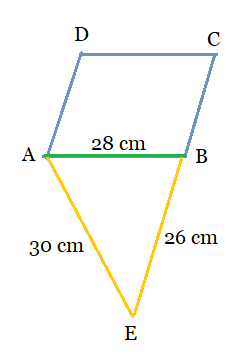1640600726893 The sides of the triangle are $a = 26\ cm,b= 28\ cm\ and\ c =30\ cm.$

Then, calculating the area of the triangle:

So, the semi-perimeter of triangle ABE,

$s = \frac{a+b+c}{2} = \frac{28+26+30}{2} = 42\ cm.$

Therefore, its area will be given by the Heron's formula:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{42(42-28)(42-26)(42-30)}$

$= \sqrt{42(14)(16)(12)} = \sqrt{112896} = 336\ cm^2$

Given that the area of the parallelogram is equal to the area of the triangle:

$Area\ of\ Parallelogram = Area\ of\ Triangle$

$\implies base\times corresponding\ height = 336\ cm^2$

$\implies 28\times corresponding\ height = 336\ cm^2$

$\implies height = \frac{336}{28} = 12\ cm.$

Hence, the height of the parallelogram is 12 cm.

Q5 A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?

Answer:

To find the area of the rhombus:

We first join the diagonal AC of quadrilateral ABCD. (See figure)

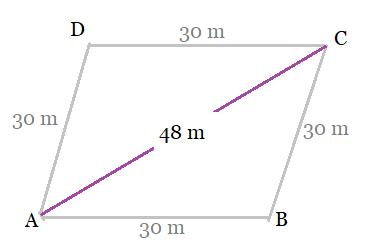1640600753242 Here, the sides of triangle ABC are,

$a = 30\ m,\ b = 30\ m\ and\ c = 48\ m.$

So, the semi-perimeter of the triangle will be:

$s = \frac{a+b+c}{2} = \frac{30+30+48}{2} = \frac{108}{2} = 54\ m$

Therefore, the area of the triangle given by the Heron's formula,

$Area = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{54(54-30)(54-30)(54-48)}$

$= \sqrt{54(24)(24)(6)} = \sqrt{186624} = 432\ m^2$

Hence, the area of the quadrilateral will be:

$= 2\times 432\ m^2 = 864\ m^2$

Therefore, the area grazed by each cow will be given by,

$= \frac{Total\ area}{Number\ of\ cows} = \frac{864}{18} = 48\ m^2.$

Q6 An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

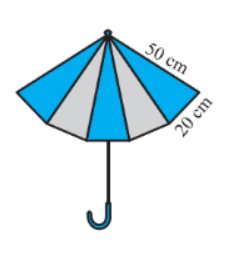1640600779979 Answer:

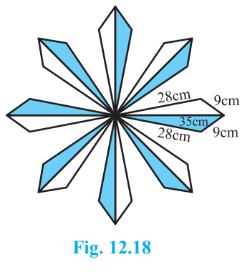
The sides of the triangle are:

$a = 20\ cm,\ b = 50\ cm\ and\ c =50\ cm.$

So, the semi-perimeter of the triangle is given by,

$s = \frac{a+b+c}{2} = \frac{20+50+50}{2} = \frac{120}{2} = 60\ cm.$

Therefore, the area of the triangle can be found by using Heron's formula:

$Area = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{60(60-20)(60-50)(60-50)}$

$= \sqrt{60(40)(10)(10)} = 200\sqrt{6}\ cm^2$

Now, for the 10 triangular pieces of cloths, the area will be,

$= 10\times200\sqrt6 = 2000\sqrt6\ cm^2$

Hence, the area of cloths of each colour will be:

$= \frac{2000\sqrt6}{2} = 1000\sqrt6\ cm^2.$

Q7 A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Figure How much paper of each shade has been used in it?

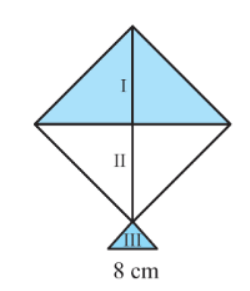1640600801509 Answer:

From the figure:

1640600823417 Calculation of the area for each shade:

The shade I: Triangle ABD

Here, base $BD = 32\ cm$ and the height $AO = 16\ cm.$

Therefore, the area of triangle ABD will be:

$= \frac{1}{2} \times base\times height = \frac{1}{2}\times 32\times 16$

$= 256\ cm^2$

Hence, the area of paper used in shade I is $256\ cm^2.$

Shade II: Triangle CBD

Here, base $BD = 32\ cm$ and height $CO = 16\ cm.$

Therefore, the area of triangle CBD will be:

$= \frac{1}{2} \times base\times height = \frac{1}{2}\times 32\times 16$

$= 256\ cm^2$

Hence, the area of paper used in shade II is $256\ cm^2.$

Shade III: Triangle CEF

Here, the sides are of lengths, $a = 6\ cm,\ b = 6\ cm\ and\ c = 8\ cm.$

So, the semi-perimeter of the triangle:

$s = \frac{a+b+c}{2} = \frac{6+6+8}{2} = \frac{20}{2} = 10\ cm.$

Therefore, the area of the triangle can be found by using Heron's formula:

$Area = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{10(10-6)(10-6)(10-8)}$

$= \sqrt{10(4)(6)(2)}$

$= 8\sqrt{5}\ cm^2$

Hence, the area of the paper used in shade III is $8\sqrt{5}\ cm^2$ .

Q8 A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm ² .

1640600847170 Answer:

GIven the sides of the triangle are:

$a = 9\ cm,\ b = 28\ cm\ and\ c= 35\ cm.$

So, its semi-perimeter will be:

$s = \frac{a+b+c}{2} = \frac{9+28+35}{2} = 36\ cm$

Therefore, the area of the triangle using Heron's formula is given by,

$Area = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{36(36-9)(36-28)(36-35)} = \sqrt{36(27)(8)(1)}$

$= \sqrt{7776} \approx 88.2\ cm^2$

So, we have the area of each triangle tile which is $88.2\ cm^2$ .

Therefore, the area of each triangular 16 tiles will be:

$= 16\times 88.2\ cm^2 = 1411.2\ cm^2$

Hence, the cost of polishing the tiles at the rate of 50 paise per cm ² will be:

$= Rs.\ 0.50\times1411.2\ cm^2 =Rs.\ 705.60$

Q9 A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.

Answer:

The trapezium field is shown below in figure:

Drawing line CF parallel to AD and a line perpendicular to AB, we obtain

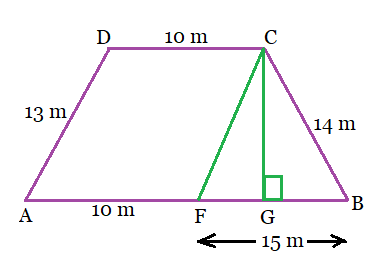1640600870807 Then in quadrilateral ADCF,

$CF || AD$ ............................ $\left [ \because\ by\ construction \right ]$

$CD || AF$ ............................ $\left [ \because ABCD\ is\ a\ trapezium \right ]$

Therefore, ADCF is a parallelogram.

So, $AD = CF = 13\ m$ and $CD = AF = 10\ m$

$\left ( \because Opposite\ sides\ of\ a\ parallelogram \right )$

Therefore, $BF = AB-AF = 25-10 = 15\ m$

Now, the sides of the triangle;

$a = 13\ m,\ b =14\ m\ and\ c = 15\ m.$

So, the semi-perimeter of the triangle will be:

$s= \frac{a+b+c}{2} = \frac{13+14+15}{2} = \frac{42}{2} = 21\ m$

Therefore, the area of the triangle can be found by using Heron's Formula:

$Area = \sqrt{s(s-a)(s-b)(s-c)}$

$= \sqrt{21(21-13)(21-14)(21-15)}$

$= \sqrt{21(8)(7)(6)}$

$= \sqrt{7056} = 84\ m^2.$

Also, the area of the triangle is given by,

$Area = \frac{1}{2}\times BF\times CG$

$\Rightarrow \frac{1}{2}\times BF\times CG = 84\ m^2$

$\Rightarrow \frac{1}{2}\times 15\times CG = 84\ m^2$

Or,

$\Rightarrow CG = \frac{84\times2}{15} = 11.2\ m$

Therefore, the area of the trapezium ABCD is:

$= \frac{1}{2} \times (AB+CD)\times CG$

$= \frac{1}{2} \times (25+10)\times 11.2$

$= 35\times5.6$

$= 196\ m^2$

Hence, the area of the trapezium field is $196\ m^2.$

Summary Of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

Chapter 12 of Class 9 Maths, "Heron’s Formula," is part of Unit 5: Mensuration, which carries a weightage of 13 marks out of 100 in the examination. Due to this, it is an essential chapter that requires thorough study. The chapter covers critical topics, including the area of a triangle using Heron’s formula and the application of Heron’s formula in finding areas of quadrilaterals. Heron's formula is used to calculate the area of a triangle using its three side lengths. Students who are interested in class 9 maths ch 12 question answer, can practice exercise using link given below.

NCERT solutions for class 9 maths - chapter wise

Chapter No.	Chapter Name
Chapter 1	Number Systems
Chapter 2	Polynomials
Chapter 3	Coordinate Geometry
Chapter 4	Linear Equations In Two Variables
Chapter 5	Introduction to Euclid's Geometry
Chapter 6	Lines And Angles
Chapter 7	Triangles
Chapter 8	Quadrilaterals
Chapter 9	Areas of Parallelograms and Triangles
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Heron’s Formula
Chapter 13	Surface Area and Volumes
Chapter 14	Statistics
Chapter 15	Probability

Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula

Comprehensive coverage: The maths chapter 12 class 9 solutions provide complete coverage of the chapter's topics, including the derivation and application of Heron's formula for finding the area of a triangle and quadrilaterals.

Easy-to-understand language: The ch 12 maths class 9 solutions use simple and easy-to-understand language, making it easier for students to comprehend the mathematical concepts and solve problems.

Helps in scoring good marks: Practising these herons formula class 9 solutions can greatly enhance a student's chances of scoring well in their exams, as the solutions provide a comprehensive understanding of the chapter's concepts.

NCERT solutions for class 9 subject wise

NCERT Solutions for Class 9 Maths

NCERT Solutions for Class 9 Science

How to use NCERT solutions for class 9 maths chapter 12 Heron's Formula?

Learn some basics about the triangles.
Read Heron's formula.
Observe its application to mathematical problems.
Now, It's time to apply the application of this formula to the practice exercises' problems.
While practicing the exercises, you can take the help of NCERT solutions for class 9 maths chapter 12 Heron's Formula.

Keep working hard and happy learning!

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. What are the important topics in chapter Heron's Formula

Area of a Triangle – by Heron’s Formula and Application of Heron’s Formula in finding Areas of Quadrilaterals are two important topics of this chapter. Students can prioritize important topics from the NCERT syllabus and study accordingly to score well in exams. for ease you can study heron's formula class 9 pdf both online and offline mode.

2. What are the key benefits of learning NCERT Solutions for class 9 chapter 12 maths?

Here are the rephrased key benefits of NCERT Solutions for Class 9 Maths Chapter 12:

The solutions for each exercise within the chapter are easily accessible for students to refer to.
The solutions are designed with graphs and illustrations that aid in providing a clear understanding of the mathematical concepts.
The solutions are meticulously prepared by the expert team at Careers360, with a strong emphasis on accuracy.

3. How does the NCERT solutions are helpful ?

NCERT solutions are helpful for the students if they are no able to solve NCERT problems on their own. Also, these solutions are provided in a very detailed manner which will give them conceptual clarity.

4. Where can I find the complete solutions of NCERT for class 9 maths ?

Here you will get the detailed NCERT solutions for class 9 maths by clicking on the link. Practicing these solutions will give you in-depth understanding of concepts which help you to score good marks in the exam.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Admit Card

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Result

Exam Pattern

Admit Card

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

Exam Pattern

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

Herons Formula Class 9 Questions And Answers PDF Free Download

Herons Formula Class 9 Solutions - Important Formulae

Herons Formula Class 9 NCERT Solutions (Intext Questions and Exercise)

Summary Of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

NCERT solutions for class 9 maths - chapter wise

Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula

NCERT solutions for class 9 subject wise

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

National Means Cum-Merit Scholarship

West Bengal Board 12th Examination

Gujarat Board Secondary School Certificate Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app