Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 12.2 Class 9 Maths Chapter 12 - Heron's Formula

NCERT Solutions for Exercise 12.2 Class 9 Maths Chapter 12 - Heron's Formula

Edited By Vishal kumar | Updated on Oct 12, 2023 12:24 PM IST

NCERT Solutions for Class 9 Maths Chapter 12: Heron's Formula Exercise 12.2- Download Free PDF

NCERT Solutions for Class 9 Maths Chapter 12: Heron’s Formula Exercise 12.2- In 9th class maths exercise 12.2 answers, you're about to become a geometry magician. Heron's Formula is your secret spell for finding triangle areas when you know the sides. class 9 maths chapter 12 exercise 12.2 is your practical practice field. It's all about solving different triangle puzzles using Heron's Formula.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 12: Heron's Formula Exercise 12.2- Download Free PDF
  2. Download PDF of NCERT Solutions for Class 9 Maths Chapter 12 – Heron’s Formula Exercise 12.2
  3. More Information About NCERT Solutions for Class 9 Maths Exercise 12.2
  4. Benefits of NCERT Solutions for Class 9 Maths Exercise 12.2
  5. Key Features of Class 9 Maths Chapter 12 Exercise 12.2
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 12.2 Class 9 Maths Chapter 12 - Heron's Formula
NCERT Solutions for Exercise 12.2 Class 9 Maths Chapter 12 - Heron's Formula

And here's the best part: You can download these exercise 12.2 class 9 maths for free in PDF. That means you can work on your magic offline, anytime you want, with these helpful guides. Let's dive into the world of triangles and Heron's Formula with confidence!

NCERT Solutions for Class 9 Maths chapter 12 exercise 12.2 is about the application of heron’s formula in finding areas of quadrilaterals. In order to solve NCERT book question for Class 9 Maths exercise 12.2, we will require information such as perimeters and areas of several of these shapes, such as rectangles and squares along with this basic area of the triangle. Heron's formula may also be used to compute the area of a quadrilateral if the quadrilaterals are divided into triangular sections. Once the quadrilaterals have been divided into triangular forms, use Heron's formula to calculate the area of individual triangular parts. Add the areas of each triangle section to get the quadrilateral's area once you've computed their areas. The following activities are included with Class 10 Mathematics chapter 12 exercise 12.2.

**As per the CBSE Syllabus for 2023-24, please note that this chapter has been renumbered as Chapter 10. So, when referring to this chapter, consider it as Chapter 10 - Heron's Formula.

Download PDF of NCERT Solutions for Class 9 Maths Chapter 12 – Heron’s Formula Exercise 12.2

Download PDF


Access Heron's Formula Class 9 Chapter 12 Exercise: 12.2

Q1 A park, in the shape of a quadrilateral ABCD, has \angle C = 90\degree , AB = 9 m , BC = 12 m , CD = 5 m and AD = 8 m . How much area does it occupy?

Answer:

From the figure:

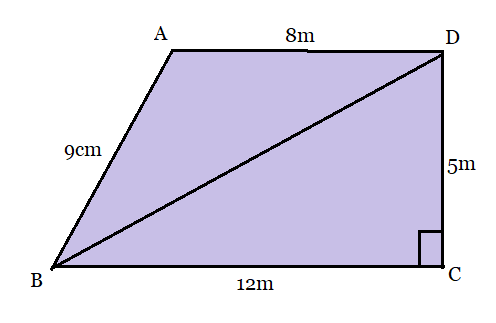
1640600614678

We have joined the BD to form two triangles so that the calculation of the area will be easy.

In triangle BCD, by Pythagoras theorem

BD^2 = BC^2+CD^2

\Rightarrow BD^2 = 12^2+5^2 = 144+25 = 169

\Rightarrow BD = 13\ cm

The area of triangle BCD can be calculated by,

Area_{(BCD)} = \frac{1}{2}\times BC\times DC = \frac{1}{2}\times 12\times 5 = 30\ cm^2

and the area of the triangle DAB can be calculated by Heron's Formula:

So, the semi-perimeter of the triangle DAB,

s = \frac{a+b+c}{2} = \frac{9+8+13}{2} = \frac{30}{2} = 15\ cm

Therefore, the area will be:

A = \sqrt{s(s-a)(s-b)(s-c)}

where, a = 9 cm,\ b = 8cm\ and\ c = 13cm .

= \sqrt{15(15-9)(15-8)(15-13)}

= \sqrt{12(6)(7)(2)} = \sqrt{1260} = 35.5\ cm^2 (Approximately)

Then, the total park area will be:

= Area\ of\ triangle\ BCD + Area\ of\ triangle\ DAB

\Rightarrow Total\ area\ of\ Park = 30+35.35 = 65.5\ cm^2

Hence, the total area of the park is 65.5\ cm^2.

Q2 Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Answer:

From the figure:

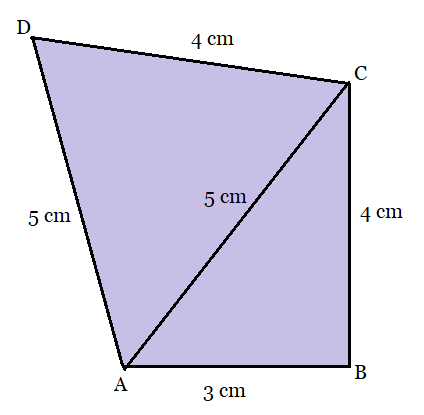
1640600632801

We have joined the AC to form two triangles so that the calculation of the area will be easy.

The area of the triangle ABC can be calculated by Heron's formula:

So, the semi-perimeter, where a = 3 cm,\ b =4cm\ and\ c = 5cm.

s = \frac{a+b+c}{2} = \frac{3+4+5}{2} = 6cm

Heron's Formula for calculating the area:

A = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{6(6-3)(6-4)(6-5)}= \sqrt{6(3)(2)(1)} = \sqrt{36} = 6\ cm^2

And the sides of the triangle ACD are a' =4cm,\ b' = 5cm\ and\ c' = 5cm.

So, the semi-perimeter of the triangle:

s' = \frac{a'+b'+c'}{2} = \frac{4+5+5}{2} = \frac{14}{2} = 7cm

Therefore, the area will be given by, Heron's formula

A = \sqrt{s'(s'-a')(s'-b')(s'-c')} .

= \sqrt{7(7-4)(7-5)(7-5)}

= \sqrt{7(3)(2)(2)} = 2\sqrt{21} = 9.2\ cm^2\ \ \ \ (Approx.)

Then, the total area of the quadrilateral will be:

= Area\ of\ triangle\ ABC + Area\ of\ triangle\ ACD

\Rightarrow Total\ area\ of\ quadrilateral\ ABCD = 6+9.2 = 15.2\ cm^2

Hence, the area of the quadrilateral ABCD is 15.2 \ cm^2.

Q3 Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

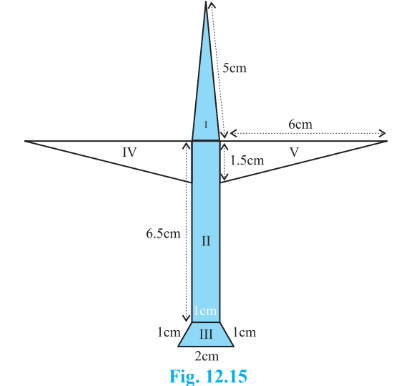1640600656571 Answer:

The total area of the paper used will be the sum of the area of the sections I, II, III, IV, and V. i.e., Total\ area = I +II+III+IV+V

For section I:

Here, the sides are a = 1cm\ and\ b =c = 5cm.

So, the Semi-perimeter will be:

s = \frac{a+b+c}{2} = \frac{5+5+1}{2} = 5.5\ cm

Therefore, the area of section I will be given by Heron's Formula,

A = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{5.5(5.5-1)(5.5-5)(5.5-5)}

= \sqrt{5.5(4.5)(0.5)(0.5)} = \sqrt{6.1875} = 2.5\ cm^2\ \ \ \ \ \ (Approx.)

For section II:

Here the sides of the rectangle are l =6.5\ cm and b =1 \ cm.

Therefore, the area of the rectangle is = l\times b = 6.5\times 1 = 6.5\ cm^2.

For section III:

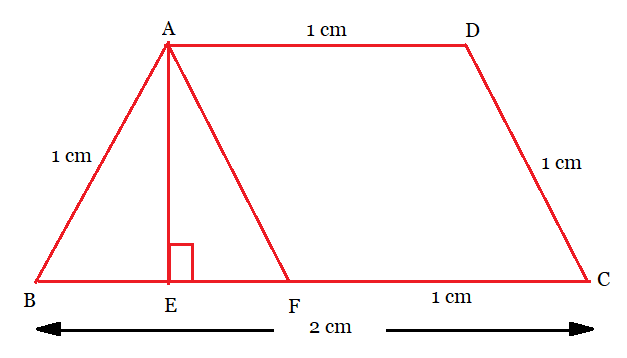
1640600697563

From the figure:

Drawing the parallel line AF to DC and a perpendicular line AE to BC.

We have the quadrilateral ADCF,

AF || DC ...........................by construction.

AD || FC ...........................[ \because ABCD is a trapezium]

So, ADCF is a parallelogram.

Therefore, AF = DC = 1\ cm and AD = FC = 1\ cm

\left [ \because Opposite\ sides\ of\ a\ parallelogram \right ]

Therefore, BF = BC -FC =2-1 = 1\ cm.

\implies ABF is an equilateral triangle. \left [ \because AB = BF =AF = 1\ cm \right ]

Then, the area of the equilateral triangle ABF is given by:

\implies \frac{\sqrt3}{4}a^2 = \frac{\sqrt3}{4}1^2 = \frac{\sqrt3}{4}

= \frac{1}{2}\times BF \times AE

= \frac{1}{2}\times 1cm \times AE = \frac{\sqrt3}{4}

\implies AE = \frac{\sqrt3}{2} = \frac{1.732}{2} = 0.866 \approx 0.9

Hence, the area of trapezium ABCD will be:

= \frac{1}{2}\times(AD+BC)\times AE

= \frac{1}{2}\times(1+2)\times 0.9

=1.35 =1.4\ cm^2\ \ \ \ (Approx.)

For Section IV:

Here, the base is 1.5 cm and the height is 6 cm.

Therefore, the area of the triangle is :

= \frac{1}{2}\times base\times height

= \frac{1}{2}\times 1.5\times 6 = 4.5\ cm^2

For section V:

The base length = 1.5cm and the height is 6cm.

Therefore, the area of the triangle will be:

= \frac{1}{2}\times 1.5\times 6 = 4.5\ cm^2

Hence, the total area of the paper used will be:

Total\ area = I +II+III+IV+V

= 2.5+6.5+1.4+4.5+4.5 = 19.4\ cm^2


Q4 A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Answer:

From the figure:

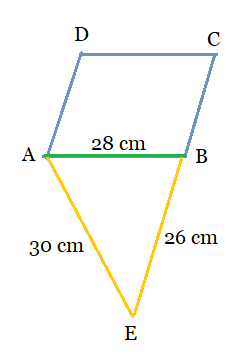1640600726893 The sides of the triangle are a = 26\ cm,b= 28\ cm\ and\ c =30\ cm.

Then, calculating the area of the triangle:

So, the semi-perimeter of triangle ABE,

s = \frac{a+b+c}{2} = \frac{28+26+30}{2} = 42\ cm.

Therefore, its area will be given by the Heron's formula:

A = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{42(42-28)(42-26)(42-30)}

= \sqrt{42(14)(16)(12)} = \sqrt{112896} = 336\ cm^2

Given that the area of the parallelogram is equal to the area of the triangle:

Area\ of\ Parallelogram = Area\ of\ Triangle

\implies base\times corresponding\ height = 336\ cm^2

\implies 28\times corresponding\ height = 336\ cm^2

\implies height = \frac{336}{28} = 12\ cm.

Hence, the height of the parallelogram is 12 cm.

Q5 A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?

Answer:

To find the area of the rhombus:

We first join the diagonal AC of quadrilateral ABCD. (See figure)

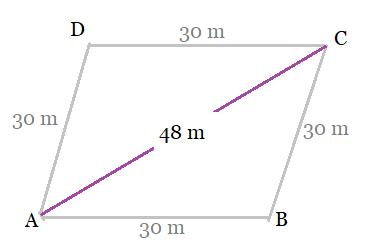1640600753242 Here, the sides of triangle ABC are,

a = 30\ m,\ b = 30\ m\ and\ c = 48\ m.

So, the semi-perimeter of the triangle will be:

s = \frac{a+b+c}{2} = \frac{30+30+48}{2} = \frac{108}{2} = 54\ m

Therefore, the area of the triangle given by the Heron's formula,

Area = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{54(54-30)(54-30)(54-48)}

= \sqrt{54(24)(24)(6)} = \sqrt{186624} = 432\ m^2

Hence, the area of the quadrilateral will be:

= 2\times 432\ m^2 = 864\ m^2

Therefore, the area grazed by each cow will be given by,

= \frac{Total\ area}{Number\ of\ cows} = \frac{864}{18} = 48\ m^2.

Q6 An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

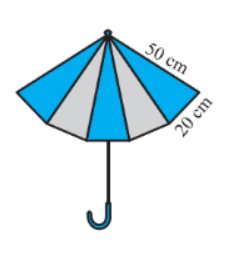1640600779979 Answer:

The sides of the triangle are:

a = 20\ cm,\ b = 50\ cm\ and\ c =50\ cm.

So, the semi-perimeter of the triangle is given by,

s = \frac{a+b+c}{2} = \frac{20+50+50}{2} = \frac{120}{2} = 60\ cm.

Therefore, the area of the triangle can be found by using Heron's formula:

Area = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{60(60-20)(60-50)(60-50)}

= \sqrt{60(40)(10)(10)} = 200\sqrt{6}\ cm^2

Now, for the 10 triangular pieces of cloths, the area will be,

= 10\times200\sqrt6 = 2000\sqrt6\ cm^2

Hence, the area of cloths of each colour will be:

= \frac{2000\sqrt6}{2} = 1000\sqrt6\ cm^2.

Q7 A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Figure How much paper of each shade has been used in it?

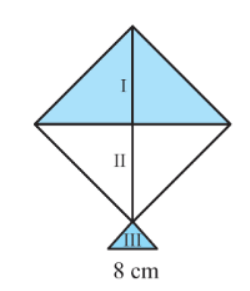1640600801509 Answer:

From the figure:

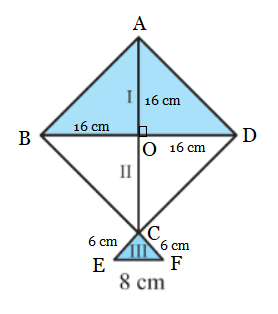1640600823417 Calculation of the area for each shade:

The shade I: Triangle ABD

Here, base BD = 32\ cm and the height AO = 16\ cm.

Therefore, the area of triangle ABD will be:

= \frac{1}{2} \times base\times height = \frac{1}{2}\times 32\times 16

= 256\ cm^2

Hence, the area of paper used in shade I is 256\ cm^2.

Shade II: Triangle CBD

Here, base BD = 32\ cm and height CO = 16\ cm.

Therefore, the area of triangle CBD will be:

= \frac{1}{2} \times base\times height = \frac{1}{2}\times 32\times 16

= 256\ cm^2

Hence, the area of paper used in shade II is 256\ cm^2.

Shade III: Triangle CEF

Here, the sides are of lengths, a = 6\ cm,\ b = 6\ cm\ and\ c = 8\ cm.

So, the semi-perimeter of the triangle:

s = \frac{a+b+c}{2} = \frac{6+6+8}{2} = \frac{20}{2} = 10\ cm.

Therefore, the area of the triangle can be found by using Heron's formula:

Area = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{10(10-6)(10-6)(10-8)}

= \sqrt{10(4)(6)(2)}

= 8\sqrt{5}\ cm^2

Hence, the area of the paper used in shade III is 8\sqrt{5}\ cm^2 .

Q8 A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm 2 .

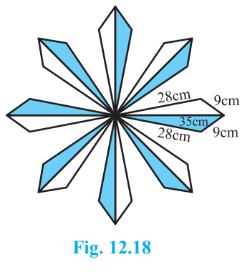1640600847170 Answer:

GIven the sides of the triangle are:

a = 9\ cm,\ b = 28\ cm\ and\ c= 35\ cm.

So, its semi-perimeter will be:

s = \frac{a+b+c}{2} = \frac{9+28+35}{2} = 36\ cm

Therefore, the area of the triangle using Heron's formula is given by,

Area = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{36(36-9)(36-28)(36-35)} = \sqrt{36(27)(8)(1)}

= \sqrt{7776} \approx 88.2\ cm^2

So, we have the area of each triangle tile which is 88.2\ cm^2 .

Therefore, the area of each triangular 16 tiles will be:

= 16\times 88.2\ cm^2 = 1411.2\ cm^2

Hence, the cost of polishing the tiles at the rate of 50 paise per cm 2 will be:

= Rs.\ 0.50\times1411.2\ cm^2 =Rs.\ 705.60


Q9 A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.

Answer:

The trapezium field is shown below in figure:

Drawing line CF parallel to AD and a line perpendicular to AB, we obtain

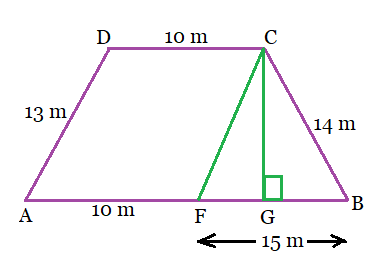1640600870807 Then in quadrilateral ADCF,

CF || AD ............................ \left [ \because\ by\ construction \right ]

CD || AF ............................ \left [ \because ABCD\ is\ a\ trapezium \right ]

Therefore, ADCF is a parallelogram.

So, AD = CF = 13\ m and CD = AF = 10\ m

\left ( \because Opposite\ sides\ of\ a\ parallelogram \right )

Therefore, BF = AB-AF = 25-10 = 15\ m

Now, the sides of the triangle;

a = 13\ m,\ b =14\ m\ and\ c = 15\ m.

So, the semi-perimeter of the triangle will be:

s= \frac{a+b+c}{2} = \frac{13+14+15}{2} = \frac{42}{2} = 21\ m

Therefore, the area of the triangle can be found by using Heron's Formula:

Area = \sqrt{s(s-a)(s-b)(s-c)}

= \sqrt{21(21-13)(21-14)(21-15)}

= \sqrt{21(8)(7)(6)}

= \sqrt{7056} = 84\ m^2.

Also, the area of the triangle is given by,

Area = \frac{1}{2}\times BF\times CG

\Rightarrow \frac{1}{2}\times BF\times CG = 84\ m^2

\Rightarrow \frac{1}{2}\times 15\times CG = 84\ m^2

Or,

\Rightarrow CG = \frac{84\times2}{15} = 11.2\ m

Therefore, the area of the trapezium ABCD is:

= \frac{1}{2} \times (AB+CD)\times CG

= \frac{1}{2} \times (25+10)\times 11.2

= 35\times5.6

= 196\ m^2

Hence, the area of the trapezium field is 196\ m^2.

More Information About NCERT Solutions for Class 9 Maths Exercise 12.2

In solving the NCERT solutions for Class 9 Maths exercise 12.2 we not only need the knowledge about how to apply the heron formula, how to find a semi perimeter but we also need the information about properties of quadrilaterals that will be helpful in solving the questions. The heron formula is not used to find the area of regular shapes like trapezium, parallelogram but we can also use the heron formula to determine the area of any irregular quadrilateral by converting the quadrilateral into triangles.

Also Read| Heron's Formula Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 12.2

  • NCERT syllabus Class 9 Maths chapter 12 exercise 12.2 broadly covers the knowledge application of heron’s formula in finding areas of quadrilaterals

  • Class 9 Maths chapter 12 exercise 12.2 is best to clear base as it covers all kinds of questions that can be formed on the application of heron’s formula in finding areas of quadrilaterals

  • Heron formula is very useful in quadrilateral as we don't need any height and angle we just need the length of sides to solve for the area

  • Heron formula can be used in entrance exams like JEE Main and to solve the question-related area of a triangle as heron formula is easier than other formulas when sides are given

Key Features of Class 9 Maths Chapter 12 Exercise 12.2

  1. Advanced Exploration of Heron's Formula: Exercise 12.2 class 9 maths builds upon the concepts introduced in Exercise 12.1, allowing students to further apply Heron's Formula to calculate the areas of triangles with given side lengths.

  2. Step-by-Step Solutions: The 9th class maths exercise 12.2 answers provide detailed, step-by-step explanations for each problem, guiding students through complex triangle area calculations.

  3. Practical Applications: This ex 12.2 class 9 challenges students with a variety of problems that require the application of Heron's Formula, enhancing their problem-solving skills in geometry.

  4. Clear and Understandable Language: Solutions are presented in clear and understandable language to ensure students can grasp the concepts with ease.

  5. PDF Format: Students can access the class 9 ex 12.2 solutions in PDF format for free download, allowing offline use and convenient learning.

Also, see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. How is heron formula used diversely in NCERT solutions for Class 9 Maths exercise 12.2 ?

There can be many alternative methods of solving the problem as we can break quadrilaterals into different types of triangles.

2. What is the information about quadrilaterals used in NCERT solutions for Class 9 Maths exercise 12.2 ?

Information such as the opposite side of a parallelogram are equal or one of the opposite sides of trapezium equal are parallel

3. What is the most common way of dividing trapezium in a triangle to apply heron formula ?

We can divide trapezium into two right-angle triangles and a rectangle 

4. What is the most common way of dividing parallelogram and rhombus in a triangle to apply heron formula?

The most common way of dividing parallelogram and rhombus  in a triangle to apply the heron formula is by diagonal 


5. What are the real life applications which we have used in Class 9 Maths chapter 12 exercise 12.2?

Floor designs, umbrella  and Paper planes are some of the real-life applications which we have used in Class 9 Maths chapter 12 exercise 12.2

6. What types of questions are included in the NCERT solution for Class 9 Mathematics exercise 12.2?

Exercise 12.2 in Class 9 Maths presents a variety of fundamental problems in which we must apply the Heron formula to a quadrilateral and provide real-life examples to make the questions more interesting to solve.

7. The number of solved examples were addressed before Class 9 Maths chapter 12 exercise 12.2 ?

There are three solved examples that were addressed before Class 9 Maths chapter 12 exercise 12.2 

8. The total number of questions answered in Class 9 Maths chapter 12 exercise 12.2 are?

The total number of questions answered in Class 9 Maths chapter 12 exercise 12.2 are 9

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

West Bengal Madhyamik examination

Result Date:02 May,2024 - 02 May,2024

Karnataka Pre-University Certificate Examination

Exam Date:02 May,2024 - 02 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance | Last Date to Apply - 30th April

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
Ranchi: 15 children injured as school bus overturns in Mandar
27/04/2024, 08:11:39
7 Intermediate students die by suicide after announcement of results in Telangana
26/04/2024, 09:53:46
Private schools hiking fee without prior approvals: Delhi Parents Association
25/04/2024, 16:50:55
Tripura schools to remain shut till April 27 due to heatwave
25/04/2024, 14:55:44
Delhi EWS Admission 2024: Registration begins from April 30; DoE issues guidelines
25/04/2024, 13:56:28
Schools, colleges in Noida to stay closed tomorrow for Lok Sabha polls 2024
25/04/2024, 07:35:49
Former CBSE academic director Joseph Emmanuel appointed CISCE chief
25/04/2024, 06:28:52
Back to top