• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 11.1 Class 9 Maths Chapter 11 - Constructions

NCERT Solutions for Exercise 11.1 Class 9 Maths Chapter 11 - Constructions

Edited By Vishal kumar | Updated on Oct 10, 2023 01:36 PM IST

NCERT Solutions for Class 9 Maths Chapter 11: Constructions Exercise 11.1- Download Free PDF

NCERT Solutions for Class 9 Maths Chapter 11: Constructions Exercise 11.1- In Chapter 9th class maths exercise 11.1 answers Maths, titled "Constructions," you'll learn how to design perfect geometric shapes with only a compass and a straightedge. This amazing journey begins with ex 11.1 class 9 It assigns you tasks that need you to precisely produce various types of angles.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 11: Constructions Exercise 11.1- Download Free PDF
  2. Download PDF of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.1
  3. Access Constructions Class 9 Maths Chapter 11 Excercise: 11.1
  4. Q5 Construct an equilateral triangle, given its side and justify the construction. Answer: The following steps to make an equilateral triangle: Step 1: Draw a line segment AB = 4 cm. Step 2: With A and B as centres, make two arcs in the line segment AB. Mark it as D and E respectively. Step 3: Now, with D and E as centres, make the two arcs cutting the previous arcs respectively, and forming an angle of each. Step 4: Extend the lines of A and B until they intersect each other at point C. Hence, triangle constructed is ABC which is equilateral. Now, Justification ; Since the angles constructed are of each, so the third angle will also be .
  5. More About NCERT Solutions for Class 9 Maths Exercise 11.1
  6. Benefits of NCERT Solutions for Class 9 Maths Exercise 11.1
  7. key Features of Class 9 Maths Chapter 11 Exercise 11.1
  8. NCERT Solutions of Class 10 Subject Wise
  9. NCERT Solutions for Class 9 Maths
NCERT Solutions for Exercise 11.1 Class 9 Maths Chapter 11 - Constructions
NCERT Solutions for Exercise 11.1 Class 9 Maths Chapter 11 - Constructions

But don't worry, because the NCERT Solutions for this class 9 maths chapter 11 exercise 11.1 serve as helpful guides. They are created by professionals and include detailed, step-by-step instructions for each construction. Plus, you can get them for free in PDF format, so you can use them even if you don't have access to the internet. So, let us begin confidently mastering the art of geometry creations!

Along with Class 9 Maths chapter 11 exercise 11.6 the following exercise is also present.

** According to the revised NCERT Syllabus 2023-24 update, this chapter has been removed.

Download PDF of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.1

Download PDF

Access Constructions Class 9 Maths Chapter 11 Excercise: 11.1

Q1 Construct an angle of 90 o at the initial point of a given ray and justify the construction.

Answer:

The steps of construction to follow:

Step 1: Draw a ray OP.

Then, take O as the centre and any radius draw an arc cutting OP at Q.

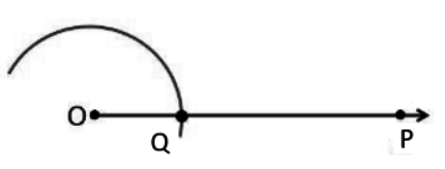
1640600746099

Step 2: Now, taking Q as the centre and with the same radius as before draw an arc cutting the previous arc at R. Repeat the process with R to cut the previous arc at S.

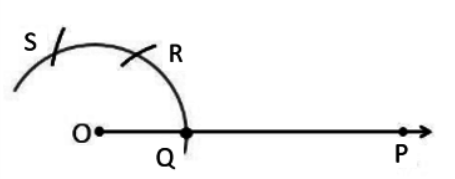
1640600957166

Step 3: Take R and S as centre draw the arc of radius more than the half of RS and draw two arcs intersecting at A. Then, join OA.

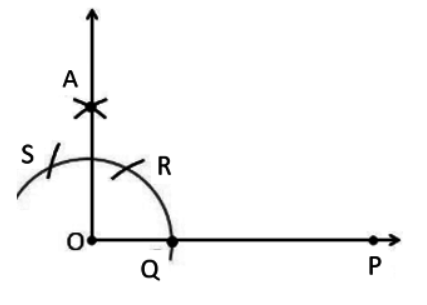
1640600972011

Hence, \angle POA = 90^{\circ } .

Justification:

We need to justify, \angle POA = 90^{\circ }

So, join OR and OS and RQ. we obtain

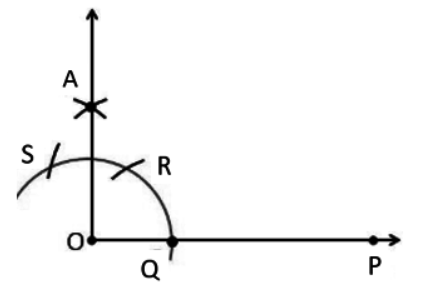
1640600984472


By construction OQ = OS = QR.

So, \triangle ROQ is an equilateral triangle. Similarly \triangle SOR is an equilateral triangle.

So, \angle SOR = 60^{\circ}

Now, \angle ROQ = 60^{\circ} that means \angle ROP = 60^{\circ} .

Then, join AS and AR:

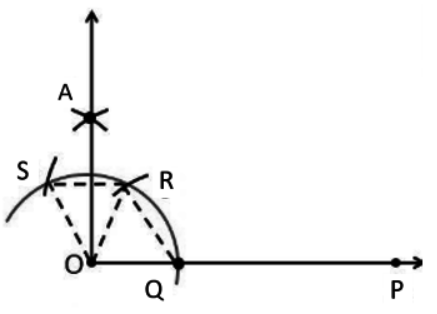
1640601001877

Now, in triangles OSA and ORA:

SR = SR (common)

AS = AR (Radii of same arcs)

OS = OR (radii of the same arcs)

So, \angle SOA = \angle ROA = \frac{1}{2}\angle SOR

Therefore, \angle ROA = 30^{\circ}

and \angle POA = \angle ROA+\angle POR = 30^{\circ} +60^{\circ} =90^{\circ}

Hence, justified.

Q2 Construct an angle of 45 o at the initial point of a given ray and justify the construction.

Answer:

The steps of construction to follow:

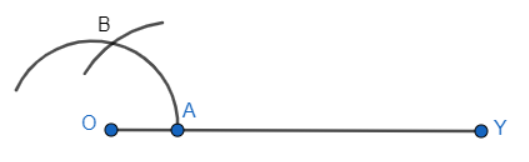
Step 1: Draw a ray OY.

Then, take O as the centre and any radius, mark a point A on the arc ABC.

1640601062706

Step 2: Now, taking A as the centre and the same radius, mark a point B on the arc ABC.

1640601050776

Step 3: Take B as a centre and the same radius, mark a point C on the arc ABC.

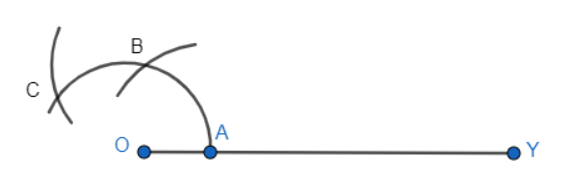
1640601072959

Step 4: Now, taking C and B as centre one by one, draw an arc from each centre intersecting each other at a point X.

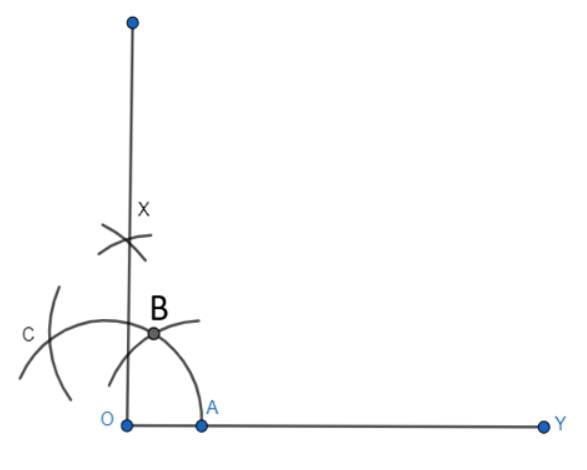
1640601086817

Step 5: X and O are joined and a ray making an angle 90^{\circ} with OY is formed.

Let the arc AC touches OX at E

Step 6: With A and E as centres, 2 arcs are marked intersecting each other at D and the bisector of angle XOY is drawn.

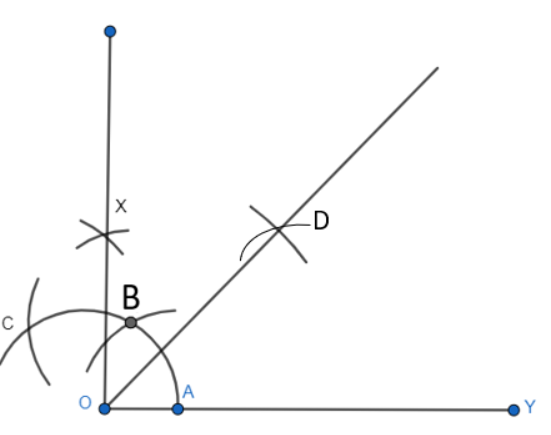
1640601100159

Justification:

By construction we have,

\angle XOY = 90^{\circ}

We constructed the bisector of \angle XOY as \angle DOY

Thus,

\angle DOY = \frac{1}{2}\angle XOY = \frac{1}{2}\times90^{\circ} = 45^{\circ}


Q3 (i) Construct the angles of the following measurements: 30 o

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601126922

Step 2: Now, take A as a center and take any radius, then draw an arc AB cutting OY at A.

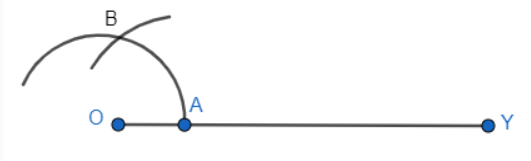
1640601139457

Step 3: Take A and B as centres, draw 2 arcs are marked intersecting each other at X and hence, the bisector of 30^{\circ} is constructed.

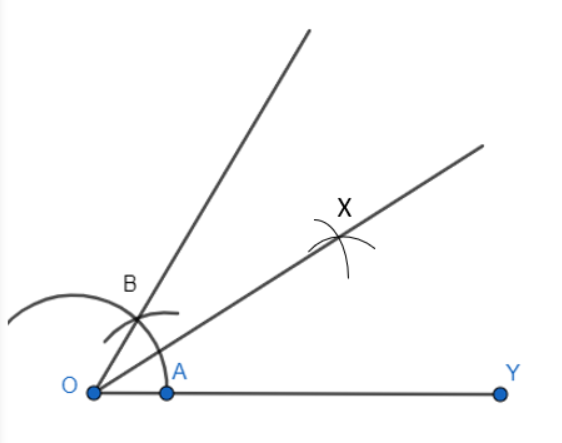
1640601151573

Thus, \angle XOY is the required angle.


Q3.Construct the angles of the following measurements: (i) 30o
Edit Q


Q3 (ii) Construct the angles of the following measurements: 22\frac{1}{2}\degree

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601174811

Step 2: Now, take A as a centre and take any radius, then mark a point B on the arc

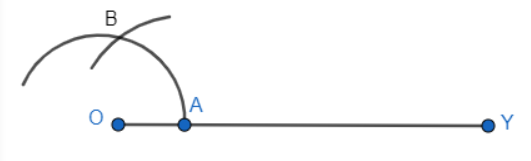
1640601184856

Step 3: Take B as a centre with the same radius, mark a point C on the arc ABC.

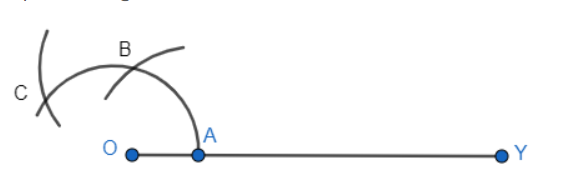
1640601195448

Step 4: Now, taking B and C as centres simultaneously, then draw an arc from each centre intersecting each other at a point X. Then join X and O and a ray making an angle with OY is formed.

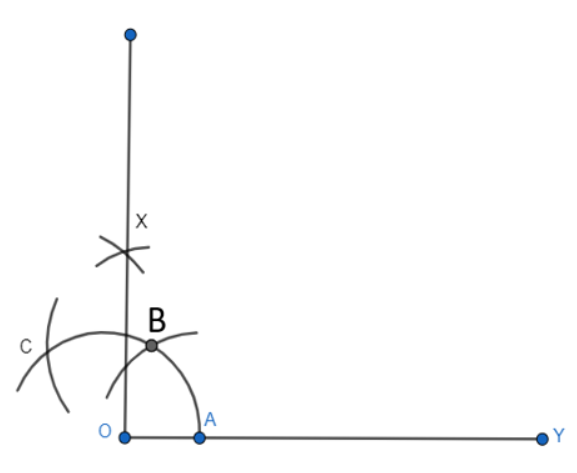
1640601206833

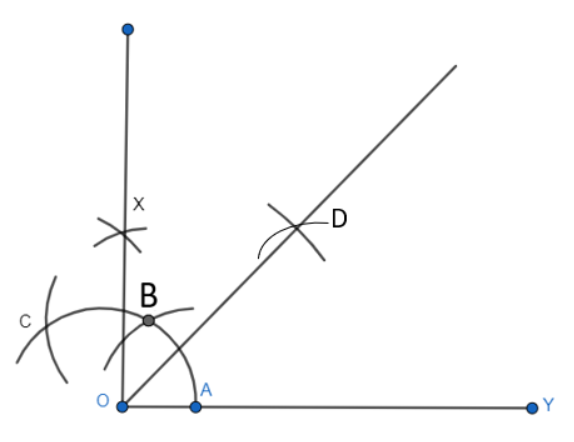
Let the arc AC touches OX at E

Step 5: Now, with A and E as centres, mark 2 arcs which intersect each other at D and we obtain the bisector of the angle XOY .

1640601218774


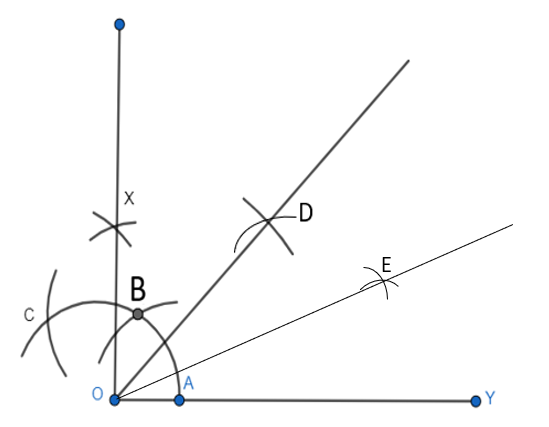
1640601229663


Q3 (iii) Construct the angles of the following measurements: 15 o

Answer:

Steps to construction to follow:

Step 1: Draw a ray OY.

1640601261458

Step 2: Now, take A as a centre and take any radius, draw an arc AB which cuts OY at A.

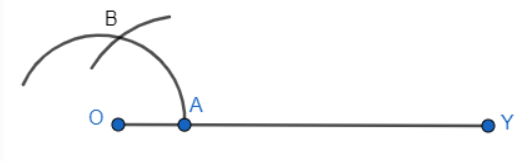
1640601272131

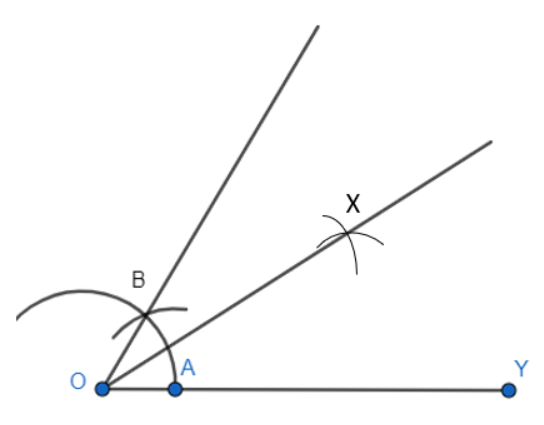
Step 3: Take A and B as a centre, then mark 2 arcs which intersect each other at X and Hence, the bisector is constructed of 30^{\circ} .

Step 4: Now, with A and E as centres, mark 2 arcs which intersect each other at D and we obtain the bisector of the angle XOY .

1640601288755

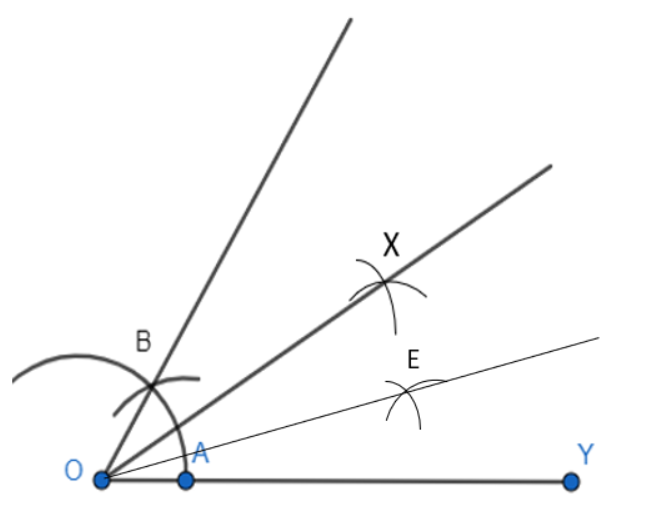
1640601299418

Thus, the angle of 15^{\circ} is obtained which is \angle EOY.

Q4 (i) Construct the following angles and verify by measuring them by a protractor: 75 o

Answer:

Steps to construction to follow:

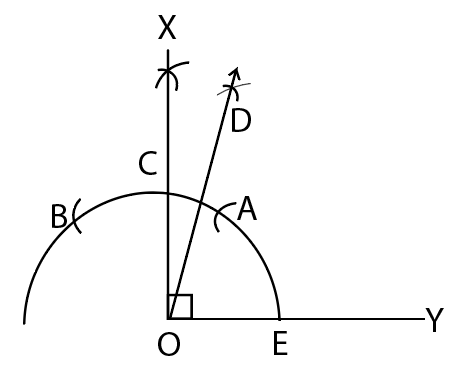
1640601336495

Step 1: Draw a ray OY.

Step 2: Now, taking O as the centre draw an arc ABC.

Step 3: On taking A as a centre, draw two arcs B and C on the arc ABC.

Step 4: Now, taking B and C as centres, arcs are made to intersect at point E and the \angle EOY = 90^{\circ} is constructed.

Step 5: Taking A and C as centres, arcs are made to intersect at D.

Step 6: Now, join OD and hence, \angle DOY = 75^{\circ} is constructed.

Hence, \angle DOY is the required angle.

Q4 (ii) Construct the following angles and verify by measuring them by a protractor: 105 o

Answer:

The steps of construction to be followed:

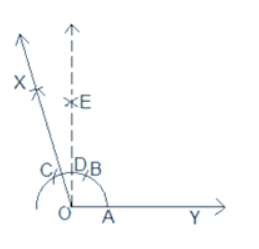
1640601361664

Step 1: Draw a ray OY.

Step 2: Then, taking O as a centre, draw an arc ABC.

Step 3: Now, with A as a centre, draw two arcs B and C which are made on the arc ABC.

Step 4: Taking B and C as centres simultaneously, arcs are made to intersect at E and \angle EOY =90^{\circ} is constructed.

Step 5: With B and C as centres, arcs are made to intersect at X.

Step 6: Join the OX and we get \angle XOY =105^{\circ} is constructed.

Thus, the angle XOY is 105^{\circ}.

Q4 (iii) Construct the following angles and verify by measuring them by a protractor: 135 o

Answer:

The steps of construction to be followed:

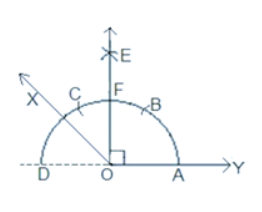
1640601385098

Step 1: Draw a ray DY.

Step 2: Draw an arc ACD with O as a center.

Step 3: Now, with A as a centre, draw two arcs B and C on the arc ACD.

Step 4: Taking B and C as centres, arcs are made to intersect at E and the angle formed is \angle EOY = 90^{\circ} .

Step 5: Take F and D as centres, draw arcs to intersect at point X or the bisector of angle EOD is made.

Step 6: Join OX and the \angle XOY = 135^{\circ} is made.

Hence, the angle required \angle XOY is 135^{\circ} .

Q5 Construct an equilateral triangle, given its side and justify the construction.

Answer:

The following steps to make an equilateral triangle:

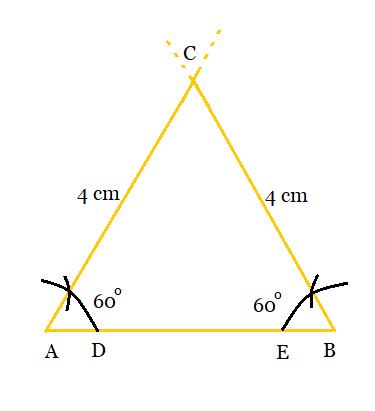
1640601397009

Step 1: Draw a line segment AB = 4 cm.

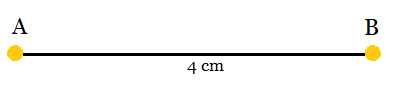
1640601407591

Step 2: With A and B as centres, make two arcs in the line segment AB. Mark it as D and E respectively.

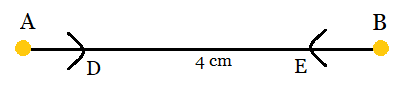
1640601419076

Step 3: Now, with D and E as centres, make the two arcs cutting the previous arcs respectively, and forming an angle of 60^{\circ } each.

Step 4: Extend the lines of A and B until they intersect each other at point C.

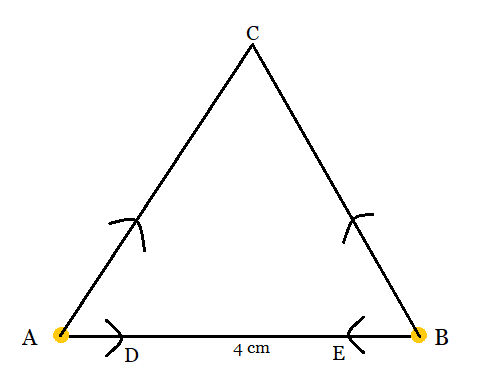
1640601431722

Hence, triangle constructed is ABC which is equilateral.

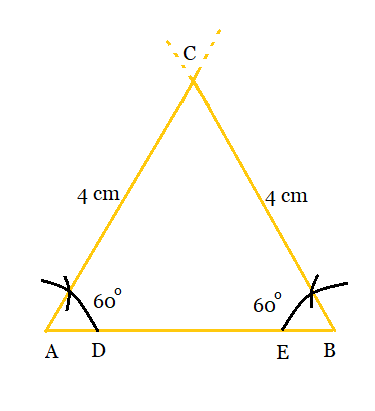
1640601440890

Now, Justification ;

Since the angles constructed are of 60^{\circ } each, so the third angle will also be 60^{\circ } .

\left [ \because The\ sum\ of\ all\ angles\ of\ triangle = 180^{\circ} \right ]



This chapter and NCERT Solutions for Class 9 Maths exercise 11.1 are majorly based on the construction like construction of angle, side bisectors and angle bisector.

NCERT solutions for exercise 11.1 Class 9 Maths chapter 11 provides us the basic core concepts which includes the construction of triangles parallelograms circles and many different complex figures which are majorly from standard 10 perspectives.

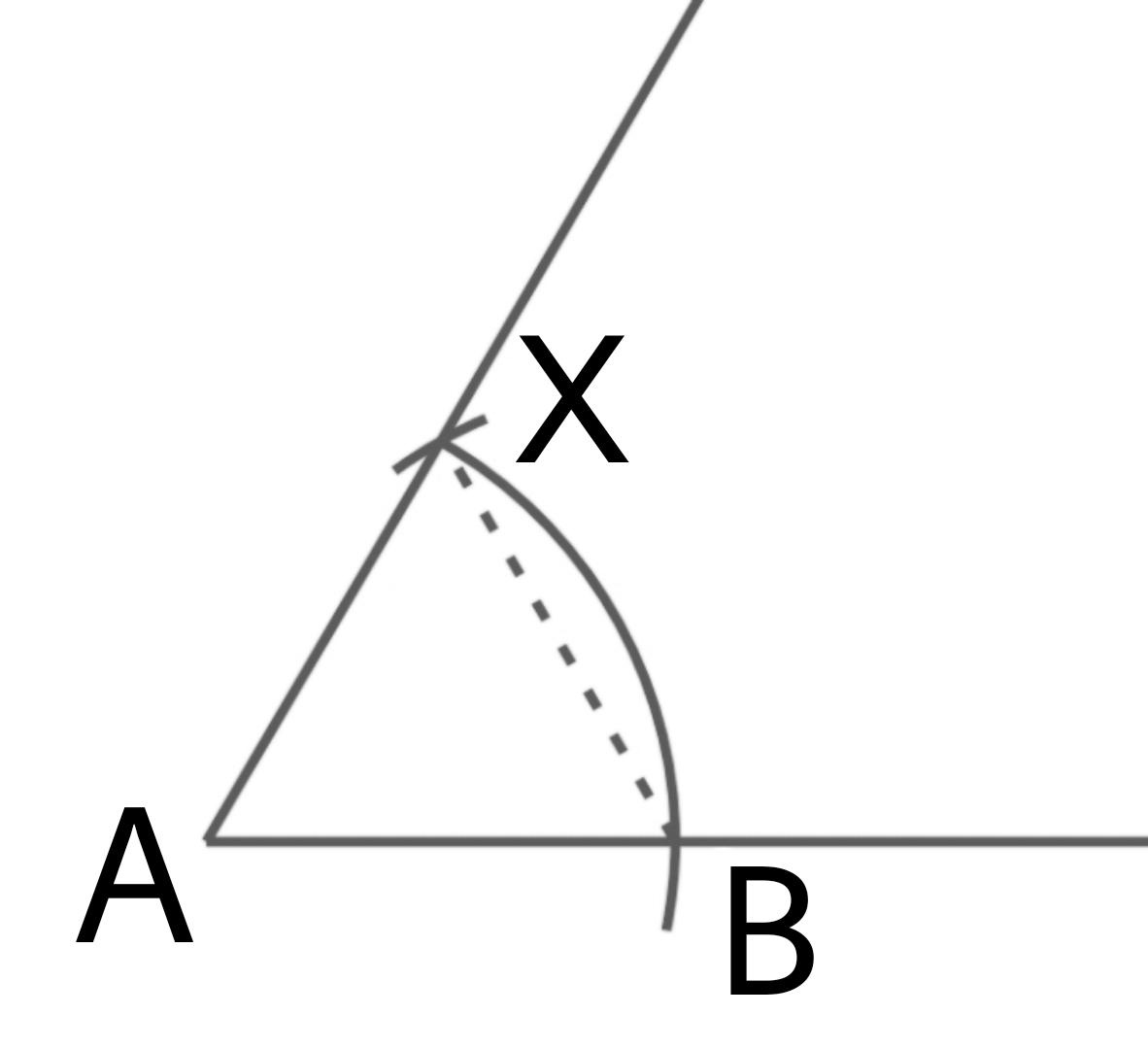
In order to drawn an angle bisector as described in NCERT solutions for Class 9 Maths chapter 11 exercise 11.1, we first draw an arc that cuts both the sides of the angle then we draw two arcs of keeping their radius larger. Thus, then we join the point where these two new arcs meet to the point of the centre of the angle this line formed is called as the angle bisector.

Figure below shows the formation of an angle bisector by following the steps from exercise 11.1 Class 9 Maths

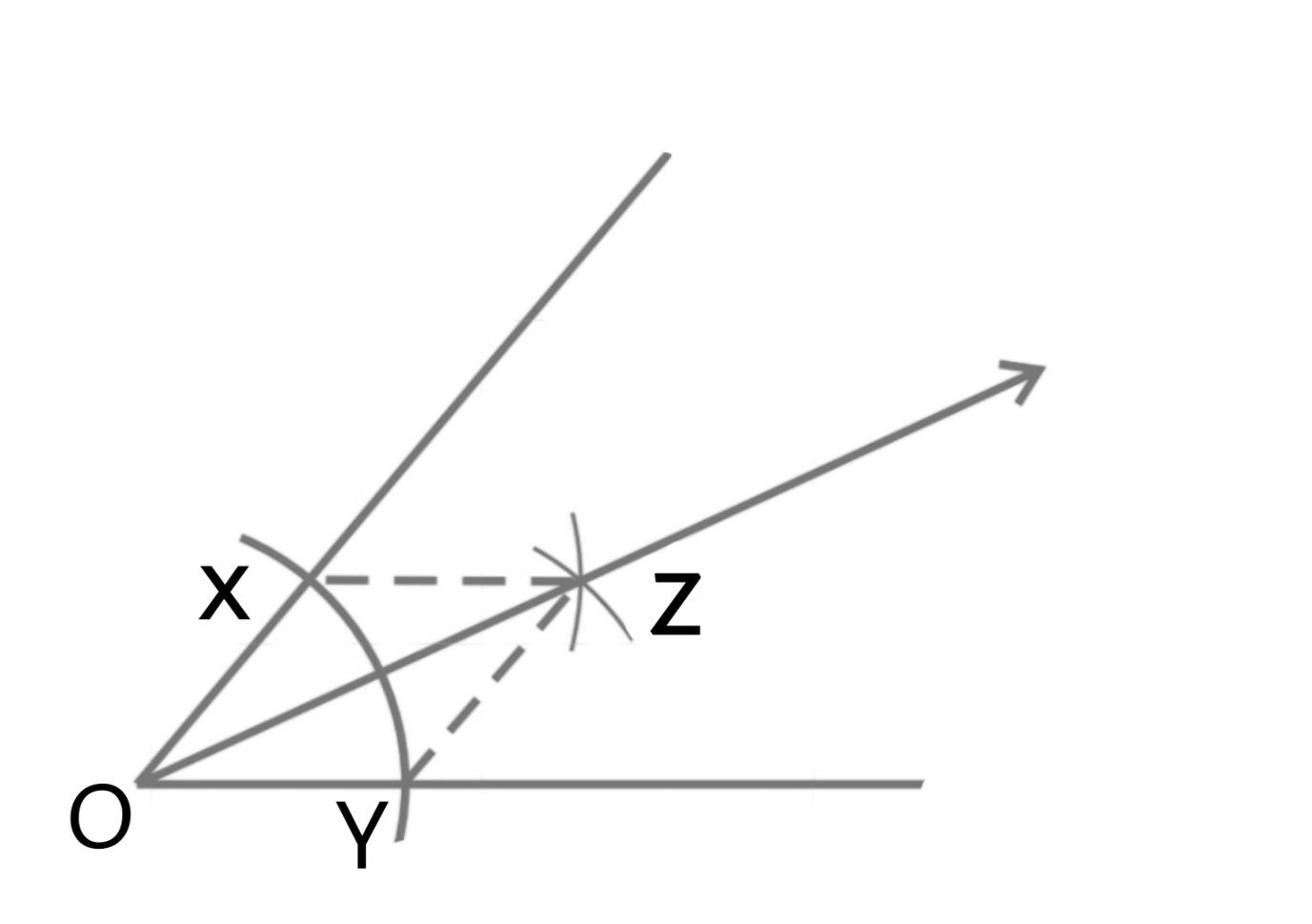
1640605777434

We follow simply this type of procedure in order to get the side bisector also

More About NCERT Solutions for Class 9 Maths Exercise 11.1

From NCERT solutions for Class 9 Maths exercise 11.1 we learn how to draw general angles for example 60 degrees. We got to know from Class 9 Maths chapter 11 exercise 11.1 that In order to draw an angle of 60 degree we first take a line mark two points at the name A&B then from A we draw an arc taking an approximation more than 60 degree and then from B we draw an arc which cuts the arc drone with centre a note that the arc radius of both the arcs drawn is equal to AB.

This we join the point a as we have taken it as the centre of the angle to the cutting point of our court the intersection points of Arc marked as X then we draw the line this angle formed is equal to 60 degrees.

1640605778546

Also Read| Constructions Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 11.1

  • Class 9 Maths chapter 11 exercise 11.1, is based construction and most of the crucial implication of construction.

  • From Class 9 Maths chapter 11 exercise 11.1 we get to learn the construction of general angles.

  • Understanding the concepts from NCERT solutions for Class 9 Maths exercise 11.1 will make the ideas and question from better expectations (like Class 10) simpler for us.

key Features of Class 9 Maths Chapter 11 Exercise 11.1

  1. Step-by-Step Solutions: NCERT Solutions for class 9 maths ex 11.1 step-by-step instructions for each construction problem. This helps students follow the process with ease.

  2. Clear and Concise: 9th class maths exercise 11.1 answers are written in clear and concise language, making it accessible for students of all levels.

  3. Accessible PDF Format: The ex 11.1 class 9 solutions are available for free download in PDF format, allowing students to access them offline and at their convenience.

  4. Concept Reinforcement: This class 9 ex 11.1 reinforces students' understanding of geometrical concepts and helps develop their construction skills, fostering attention to detail.

  5. Preparation for Advanced Topics: The constructions taught in this chapter are foundational for more advanced topics in geometry that students will encounter in higher classes.

Also, See

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. What is the core concept for NCERT solutions for Class 9 maths exercise 11.1?

This Exercise deals with the general construction of side bisector and angle bisector along with the making of some general angles.

2. How can you define an angle bisector?

An angle bisector is a line or beam that separates an angle into two harmonious or equivalent points.

3. What is a side bisector?

A side bisector is a line that divides the line segment into congruent parts. It makes an angle of 90° with the line that is being bisected.

4. How many side bisectors are possible for a triangle?

A triangle has three side bisectors, each one for its sides.

5. Can we get 45-degree angle if we are given an angle of 90 degrees?

Yes, we can get 45 degrees if we just bisect the right angle (90 degree) into two equal halves.

6. For a given angle how many bisectors are possible?

Two bisectors are possible for a given angle. Interior and exterior angle bisector.

7. For a given line segment how many bisectors are possible?

A line segment has a maximum of only one side bisector unlike that of an angle.

8. Can we get an angle of 15 degrees from a given angle of 60 degree ?

Yes, we can get an angle of 15 degrees from the given angle of 60 Degree. First, we have to bisect the 60 degree angle into two 30 degrees then further bisect the 30 degree angle into two parts, thus we will end up with a 15 degree angle.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
MP: Private schools to pay back illegally collected tuition fees worth Rs 31 crores
Tamil Nadu teacher fatally stabbed in school, violence erupts; assailant detained
Bihar govt puts hold on new teachers transfer policy
Youth stabs teacher on school premises; now detained, says police
Air Pollution: Schools in Rajasthan's Khairthal-Tijara go online for classes 1 to 5
Govt informs SC about NCERT guidelines for development of e-content for children with disabilities
Government school principal in Andhra chops off girl students' hair for coming late
Back to top